两万字长文，看看常见的系统设计题！ - 哈喽比特

大家好，系统设计题是目前面试中比较难掌握的一部分，今天这篇文章来聊聊怎么准备这部分内容，文章主要分三个部分：面试时回答系统设计题的思路、系统的一些性能指标、经典系统设计题及答案。

文章目录：

面试时回答系统设计题的思路
系统的一些性能指标
经典系统设计题与思路
分布式ID生成器
短网址系统
定时任务调度器
最近一个小时内访问频率最高的10个IP
key-Value存储引擎
Manifest文件
Log文件
数据流采样
基数估计
频率估计
Top k频繁项
范围查询
成员查询

面试时回答系统设计题的思路

这部分内容主要参考了Github的一个国外的开源项目，写的很好，感兴趣的小伙伴可以去看看：https://github.com/donnemartin/system-design-primer

常见的系统设计题有设计一个秒杀系统、红包雨、URL短网址等，完成一个系统设计题大概需要分为四步。

需要注意的是，在面试过程中是比较紧张的，但遇到这种系统设计题，一定先不要急着回答，一定要先需要设计系统的一些使用场景。

第一步：像面试官不断提问，搞清楚系统的使用场景

系统的功能是什么
系统的目标群体是什么
系统的用户量有多大
希望每秒钟处理多少请求？
希望处理多少数据？
希望的读写比率？

2 . 第二步：创造一个高层级的设计

画出主要的组件和连接

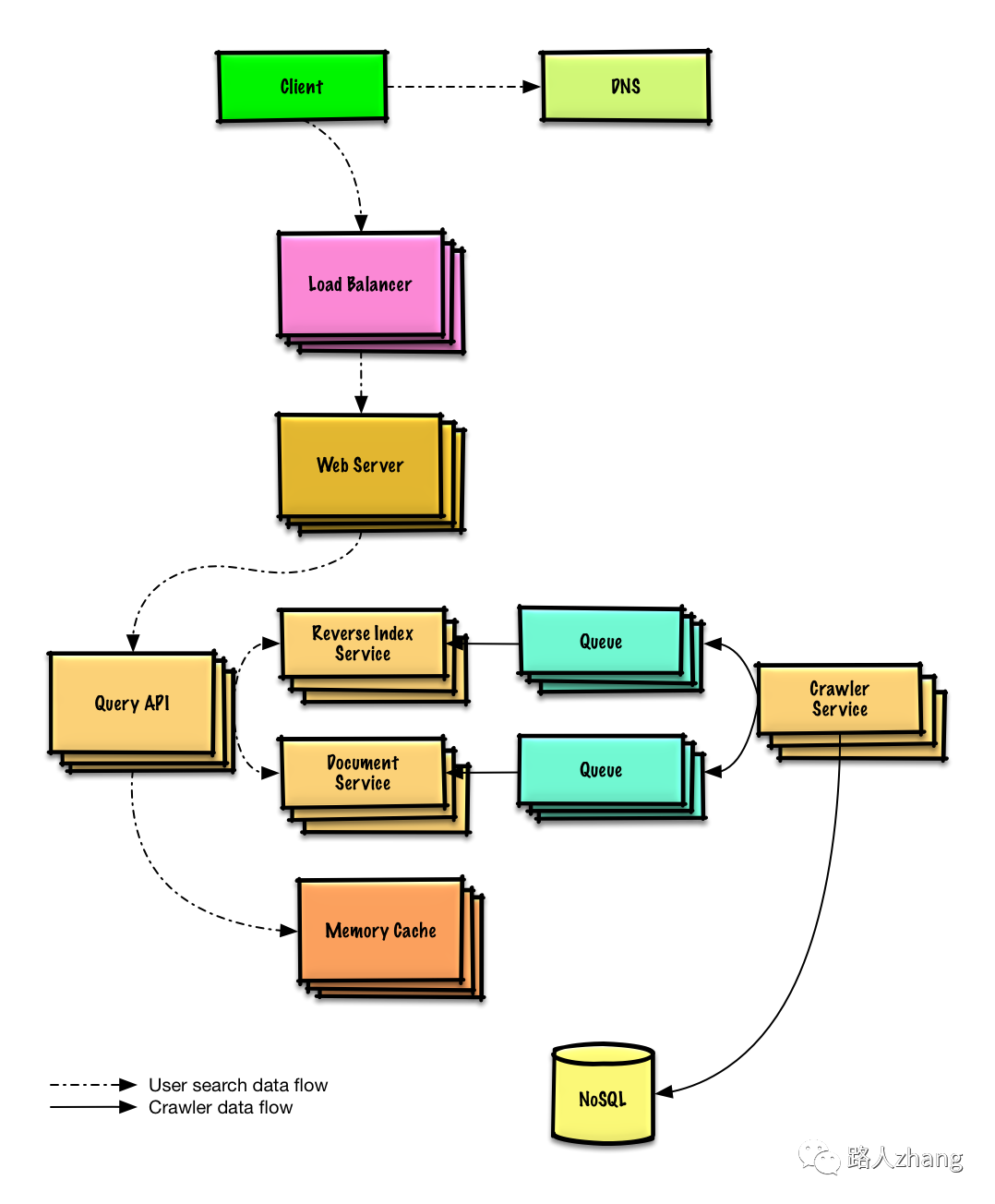
例如设计一个网络爬虫，这个是个完整的架构图，在这一步只需要画出一个抽象的架构图即可，不需要这么具体。

3 . 设计核心组件

对每一个核心组件进行具体地分析。例如，面试官让你设计一个url短网址，你需要考虑这些问题

数据库查找
MD5和 Base62
Hash 碰撞
SQL 还是 NoSQL
数据库模型
生成并储存一个完整 url 的 hash
将一个 hashed url 翻译成完整的 url
API 和面向对象设计

4 . 对系统进行优化

找到系统的瓶颈所在，对其进行优化，例如可以考虑水平扩展、数据库分片等等。

系统的一些性能指标

1 . 响应时间

响应时间指从发出请求开始到收到最后响应数据所需的时间，响应时间是系统最重要的性能指标其直观地反映了系统的“快慢”。

2 . 并发数

并发数指系统能够同时处理请求的数目，这个数字反映了系统的负载特性。

3 . 吞吐量

吞吐量指单位时间内系统处理的请求数量，体现系统的整体处理能力。

QPS（Query Per Second）：服务器每秒可以执行的查询次数

TPS（Transaction Per Second）：服务器每秒处理的事务数

并发数=QPS*平均响应时间

4 . 经常听到的一些系统活跃度的名词

PV（Page View）

页面点击量或者浏览量，用户每次对网站中的每个页面访问均被记录一个PV，多次访问则会累计。
UV（Unique visitor）

独立访客，统计一天内访问网站的用户数，一个用户多次访问网站算一个用户
IP（Internet Protocol）

指一天内访问某站点的IP总数，以用户的IP地址作为统计的指标，相同IP多次访问某站点算一次

IP和UV的区别：

在同一个IP地址下，两个不同的账号访问同一个站点，UV算两次，IP算一次
DAU（Daily Active User）：日活跃用户数量。
MAU(monthly active users)：月活跃用户人数。

5 . 常用软件的QPS

通过了解这些软件的QPS可以更清楚地找出系统的瓶颈所在。

Nginx：一般Nginx的QPS是比较大的，单机的可达到30万
MySQL：对于读操作可达几百k，对于写操作更低，大概只有100k
Redis：大概在几万左右，像set命令甚至可达10万
Tomcat：单机 Tomcat 的QPS 在 2万左右。
Memcached：大概在几十万左右

经典系统设计题与思路

这里列举了一些比较经典的系统设计题，并给出了解题思路，该部分内容来源于Gitbook，链接：https://github.com/donnemartin/system-design-primer

分布式ID生成器

如何设计一个分布式ID生成器(Distributed ID Generator)，并保证ID按时间粗略有序？

应用场景(Scenario)

现实中很多业务都有生成唯一ID的需求，例如：

用户ID
微博ID
聊天消息ID
帖子ID
订单ID

需求(Needs)

这个ID往往会作为数据库主键，所以需要保证全局唯一。数据库会在这个字段上建立聚集索引(Clustered Index，参考 MySQL InnoDB)，即该字段会影响各条数据再物理存储上的顺序。

ID还要尽可能短，节省内存，让数据库索引效率更高。基本上64位整数能够满足绝大多数的场景，但是如果能做到比64位更短那就更好了。需要根据具体业务进行分析，预估出ID的最大值，这个最大值通常比64位整数的上限小很多，于是我们可以用更少的bit表示这个ID。

查询的时候，往往有分页或者排序的需求，所以需要给每条数据添加一个时间字段，并在其上建立普通索引(Secondary Index)。但是普通索引的访问效率比聚集索引慢，如果能够让ID按照时间粗略有序，则可以省去这个时间字段。为什么不是按照时间精确有序呢？因为按照时间精确有序是做不到的，除非用一个单机算法，在分布式场景下做到精确有序性能一般很差。

这就引出了ID生成的三大核心需求：

全局唯一(unique)
按照时间粗略有序(sortable by time)
尽可能短

下面介绍一些常用的生成ID的方法。

UUID

用过MongoDB的人会知道，MongoDB会自动给每一条数据赋予一个唯一的ObjectId,保证不会重复，这是怎么做到的呢？实际上它用的是一种UUID算法，生成的ObjectId占12个字节，由以下几个部分组成，

4个字节表示的Unix timestamp,
3个字节表示的机器的ID
2个字节表示的进程ID
3个字节表示的计数器

UUID是一类算法的统称，具体有不同的实现。UUID的优点是每台机器可以独立产生ID，理论上保证不会重复，所以天然是分布式的，缺点是生成的ID太长，不仅占用内存，而且索引查询效率低。

多台MySQL服务器

既然MySQL可以产生自增ID，那么用多台MySQL服务器，能否组成一个高性能的分布式发号器呢？显然可以。

假设用8台MySQL服务器协同工作，第一台MySQL初始值是1，每次自增8，第二台MySQL初始值是2，每次自增8，依次类推。前面用一个 round-robin load balancer 挡着，每来一个请求，由 round-robin balancer 随机地将请求发给8台MySQL中的任意一个，然后返回一个ID。

Flickr就是这么做的，仅仅使用了两台MySQL服务器。可见这个方法虽然简单无脑，但是性能足够好。不过要注意，在MySQL中，不需要把所有ID都存下来，每台机器只需要存一个MAX_ID就可以了。这需要用到MySQL的一个REPLACE INTO特性。

这个方法跟单台数据库比，缺点是ID是不是严格递增的，只是粗略递增的。不过这个问题不大，我们的目标是粗略有序，不需要严格递增。

Twitter Snowflake

比如 Twitter 有个成熟的开源项目，就是专门生成ID的，Twitter Snowflake 。Snowflake的核心算法如下：

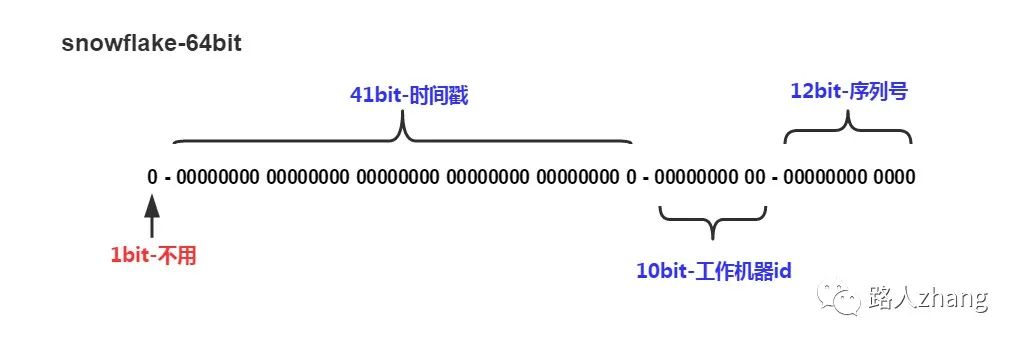
最高位不用，永远为0，其余三组bit占位均可浮动，看具体的业务需求而定。默认情况下41bit的时间戳可以支持该算法使用到2082年，10bit的工作机器id可以支持1023台机器，序列号支持1毫秒产生4095个自增序列id。

Instagram用了类似的方案，41位表示时间戳，13位表示shard Id(一个shard Id对应一台PostgreSQL机器),最低10位表示自增ID，怎么样，跟Snowflake的设计非常类似吧。这个方案用一个PostgreSQL集群代替了Twitter Snowflake 集群，优点是利用了现成的PostgreSQL，容易懂，维护方便。

有的面试官会问，如何让ID可以粗略的按照时间排序？上面的这种格式的ID，含有时间戳，且在高位，恰好满足要求。如果面试官又问，如何保证ID严格有序呢？在分布式这个场景下，是做不到的，要想高性能，只能做到粗略有序，无法保证严格有序。

短网址系统

如何设计一个短网址服务(TinyURL)？

使用场景(Scenario)

微博和Twitter都有140字数的限制，如果分享一个长网址，很容易就超出限制，发布出去。短网址服务可以把一个长网址变成短网址，方便在社交网络上传播。

需求(Needs)

很显然，要尽可能的短。长度设计为多少才合适呢？

短网址的长度

当前互联网上的网页总数大概是 45亿(参考 http://www.worldwidewebsize.com)，45亿超过了 2^{32}=4294967296232=4294967296，但远远小于64位整数的上限值，那么用一个64位整数足够了。

微博的短网址服务用的是长度为7的字符串，这个字符串可以看做是62进制的数，那么最大能表示{62}^7=3521614606208627=3521614606208个网址，远远大于45亿。所以长度为7就足够了。

一个64位整数如何转化为字符串呢？，假设我们只是用大小写字母加数字，那么可以看做是62进制数，log_{62} {(2^{64}-1)}=10.7log62(264−1)=10.7，即字符串最长11就足够了。

实际生产中，还可以再短一点，比如新浪微博采用的长度就是7，因为 62^7=3521614606208627=3521614606208，这个量级远远超过互联网上的URL总数了，绝对够用了。

现代的web服务器（例如Apache, Nginx）大部分都区分URL里的大小写了，所以用大小写字母来区分不同的URL是没问题的。

因此，正确答案：长度不超过7的字符串，由大小写字母加数字共62个字母组成

一对一还是一对多映射？

一个长网址，对应一个短网址，还是可以对应多个短网址？这也是个重大选择问题

一般而言，一个长网址，在不同的地点，不同的用户等情况下，生成的短网址应该不一样，这样，在后端数据库中，可以更好的进行数据分析。如果一个长网址与一个短网址一一对应，那么在数据库中，仅有一行数据，无法区分不同的来源，就无法做数据分析了。

以这个7位长度的短网址作为唯一ID，这个ID下可以挂各种信息，比如生成该网址的用户名，所在网站，HTTP头部的 User Agent等信息，收集了这些信息，才有可能在后面做大数据分析，挖掘数据的价值。短网址服务商的一大盈利来源就是这些数据。

正确答案：一对多

如何计算短网址

现在我们设定了短网址是一个长度为7的字符串，如何计算得到这个短网址呢？

最容易想到的办法是哈希，先hash得到一个64位整数，将它转化为62进制整，截取低7位即可。但是哈希算法会有冲突，如何处理冲突呢，又是一个麻烦。这个方法只是转移了矛盾，没有解决矛盾，抛弃。

**正确答案：**分布式ID生成器

如何存储

如果存储短网址和长网址的对应关系？以短网址为 primary key, 长网址为value, 可以用传统的关系数据库存起来，例如MySQL, PostgreSQL，也可以用任意一个分布式KV数据库，例如Redis, LevelDB。

如果你手痒想要手工设计这个存储，那就是另一个话题了，你需要完整地造一个KV存储引擎轮子。当前流行的KV存储引擎有LevelDB和RockDB，去读它们的源码吧

301还是302重定向

这也是一个有意思的问题。这个问题主要是考察你对301和302的理解，以及浏览器缓存机制的理解。

301是永久重定向，302是临时重定向。短地址一经生成就不会变化，所以用301是符合http语义的。但是如果用了301， Google，百度等搜索引擎，搜索的时候会直接展示真实地址，那我们就无法统计到短地址被点击的次数了，也无法收集用户的Cookie, User Agent 等信息，这些信息可以用来做很多有意思的大数据分析，也是短网址服务商的主要盈利来源。

所以，正确答案是302重定向。

可以抓包看看新浪微博的短网址是怎么做的，使用 Chrome 浏览器，访问这个URL http://t.cn/RX2VxjI，是我事先发微博自动生成的短网址。来抓包看看返回的结果是啥

可见新浪微博用的就是302临时重定向。

预防攻击

如果一些别有用心的黑客，短时间内向TinyURL服务器发送大量的请求，会迅速耗光ID，怎么办呢？

首先，限制IP的单日请求总数，超过阈值则直接拒绝服务。

光限制IP的请求数还不够，因为黑客一般手里有上百万台肉鸡的，IP地址大大的有，所以光限制IP作用不大。

可以用一台Redis作为缓存服务器，存储的不是 ID->长网址，而是长网址->ID，仅存储一天以内的数据，用LRU机制进行淘汰。这样，如果黑客大量发同一个长网址过来，直接从缓存服务器里返回短网址即可，他就无法耗光我们的ID了。

定时任务调度器

请实现一个定时任务调度器，有很多任务，每个任务都有一个时间戳，任务会在该时间点开始执行。

定时执行任务是一个很常见的需求，例如Uber打车48小时后自动好评，淘宝购物15天后默认好评，等等。

方案1: PriorityBlockingQueue + Polling

我们很快可以想到第一个办法：

用一个java.util.concurrent.PriorityBlockingQueue来作为优先队列。因为我们需要一个优先队列，又需要线程安全，用PriorityBlockingQueue再合适不过了。你也可以手工实现一个自己的PriorityBlockingQueue，用java.util.PriorityQueue + ReentrantLock，用一把锁把这个队列保护起来，就是线程安全的啦
对于生产者，可以用一个while(true)，造一些随机任务塞进去
对于消费者，起一个线程，在 while(true)里每隔几秒检查一下队列，如果有任务，则取出来执行。

这个方案的确可行，总结起来就是轮询(polling)。轮询通常有个很大的缺点，就是时间间隔不好设置，间隔太长，任务无法及时处理，间隔太短，会很耗CPU。

方案2: PriorityBlockingQueue + 时间差

可以把方案1改进一下，while(true)里的逻辑变成：

偷看一下堆顶的元素，但并不取出来，如果该任务过期了，则取出来
如果没过期，则计算一下时间差，然后 sleep()该时间差

不再是 sleep() 一个固定间隔了，消除了轮询的缺点。

稍等！这个方案其实有个致命的缺陷，导致它比 PiorityBlockingQueue + Polling 更加不可用，这个缺点是什么呢？。。。假设当前堆顶的任务在100秒后执行，消费者线程peek()偷看到了后，开始sleep 100秒，这时候一个新的任务插了进来，该任务在10秒后应该执行，但是由于消费者线程要睡眠100秒，这个新任务无法及时处理

方案3: DelayQueue

方案2虽然已经不错了，但是还可以优化一下，Java里有一个DelayQueue，完全符合题目的要求。DelayQueue 设计得非常巧妙，可以看做是一个特化版的PriorityBlockingQueue，它把计算时间差并让消费者等待该时间差的功能集成进了队列，消费者不需要关心时间差的事情了，直接在while(true)里不断take()就行了。

DelayQueue的实现原理见下面的代码。

import java.util.PriorityQueue;
import java.util.concurrent.Delayed;
import java.util.concurrent.locks.Condition;
import java.util.concurrent.locks.ReentrantLock;

import static java.util.concurrent.TimeUnit.NANOSECONDS;

public class DelayQueue<E extends Delayed> {
    private final transient ReentrantLock lock = new ReentrantLock();
    private final PriorityQueue<E> q = new PriorityQueue<E>();
    private final Condition available = lock.newCondition();
    private Thread leader = null;

    public DelayQueue() {}

    /**
     * Inserts the specified element into this delay queue.
     *
     * @param e the element to add
     * @return {@code true}
     * @throws NullPointerException if the specified element is null
     */
    public boolean put(E e) {
        final ReentrantLock lock = this.lock;
        lock.lock();
        try {
            q.offer(e);
            if (q.peek() == e) {
                leader = null;
                available.signal();
            }
            return true;
        } finally {
            lock.unlock();
        }
    }

    /**
     * Retrieves and removes the head of this queue, waiting if necessary
     * until an element with an expired delay is available on this queue.
     *
     * @return the head of this queue
     * @throws InterruptedException {@inheritDoc}
     */
    public E take() throws InterruptedException {
        final ReentrantLock lock = this.lock;
        lock.lockInterruptibly();
        try {
            for (;;) {
                E first = q.peek();
                if (first == null)
                    available.await();
                else {
                    long delay = first.getDelay(NANOSECONDS);
                    if (delay <= 0)
                        return q.poll();
                    first = null; // don't retain ref while waiting
                    if (leader != null)
                        available.await();
                    else {
                        Thread thisThread = Thread.currentThread();
                        leader = thisThread;
                        try {
                            available.awaitNanos(delay);
                        } finally {
                            if (leader == thisThread)
                                leader = null;
                        }
                    }
                }
            }
        } finally {
            if (leader == null && q.peek() != null)
                available.signal();
            lock.unlock();
        }
    }
}

这个代码中有几个要点要注意一下。

1. put()方法

if (q.peek() == e) {
    leader = null;
    available.signal();
}

如果第一个元素等于刚刚插入进去的元素，说明刚才队列是空的。现在队列里有了一个任务，那么就应该唤醒所有在等待的消费者线程，避免了方案2的缺点。将leader重置为null，这些消费者之间互相竞争，自然有一个会被选为leader。

2. 线程leader的作用

leader这个成员有啥作用？DelayQueue的设计其实是一个Leader/Follower模式，leader就是指向Leader线程的。该模式可以减少不必要的等待时间，当一个线程是Leader时，它只需要一个时间差；其他Follower线程则无限等待。比如头节点任务还有5秒就要开始了，那么Leader线程会sleep 5秒，不需要傻傻地等待固定时间间隔。

想象一下有个多个消费者线程用take方法去取任务,内部先加锁,然后每个线程都去peek头节点。如果leader不为空说明已经有线程在取了，让当前消费者无限等待。

if (leader != null)
   available.await();

如果为空说明没有其他消费者去取任务,设置leader为当前消费者，并让改消费者等待指定的时间，

else {
    Thread thisThread = Thread.currentThread();
    leader = thisThread;
    try {
         available.awaitNanos(delay);
    } finally {
         if (leader == thisThread)
             leader = null;
    }
}

下次循环会走如下分支，取到任务结束，

if (delay <= 0)
    return q.poll();

3. take()方法中为什么释放first

first = null; // don't retain ref while waiting

我们可以看到 Doug Lea 后面写的注释，那么这行代码有什么用呢？

如果删除这行代码，会发生什么呢？假设现在有3个消费者线程，

线程A进来获取first,然后进入 else 的 else ,设置了leader为当前线程A，并让A等待一段时间
线程B进来获取first, 进入else的阻塞操作,然后无限期等待，这时线程B是持有first引用的
线程A等待指定时间后被唤醒，获取对象成功，出队，这个对象理应被GC回收，但是它还被线程B持有着，GC链可达，所以不能回收这个first
只要线程B无限期的睡眠，那么这个本该被回收的对象就不能被GC销毁掉，那么就会造成内存泄露

Task对象

import java.util.concurrent.Delayed;
import java.util.concurrent.TimeUnit;

public class Task implements Delayed {
    private String name;
    private long startTime;  // milliseconds

    public Task(String name, long delay) {
        this.name = name;
        this.startTime = System.currentTimeMillis() + delay;
    }

    @Override
    public long getDelay(TimeUnit unit) {
        long diff = startTime - System.currentTimeMillis();
        return unit.convert(diff, TimeUnit.MILLISECONDS);
    }

    @Override
    public int compareTo(Delayed o) {
        return (int)(this.startTime - ((Task) o).startTime);
    }

    @Override
    public String toString() {
        return "task " + name + " at " + startTime;
    }
}

JDK中有一个接口java.util.concurrent.Delayed，可以用于表示具有过期时间的元素，刚好可以拿来表示任务这个概念。

生产者

import java.util.Random;
import java.util.UUID;

public class TaskProducer implements Runnable {
    private final Random random = new Random();
    private DelayQueue<Task> q;

    public TaskProducer(DelayQueue<Task> q) {
        this.q = q;
    }

    @Override
    public void run() {
        while (true) {
            try {
                int delay = random.nextInt(10000);
                Task task = new Task(UUID.randomUUID().toString(), delay);
                System.out.println("Put " + task);
                q.put(task);
                Thread.sleep(3000);
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
        }
    }
}

生产者很简单，就是一个死循环，不断地产生一些是时间随机的任务。

消费者

public class TaskConsumer implements Runnable {
    private DelayQueue<Task> q;

    public TaskConsumer(DelayQueue<Task> q) {
        this.q = q;
    }

    @Override
    public void run() {
        while (true) {
            try {
                Task task = q.take();
                System.out.println("Take " + task);
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
        }
    }
}

当 DelayQueue 里没有任务时，TaskConsumer会无限等待，直到被唤醒，因此它不会消耗CPU。

定时任务调度器

public class TaskScheduler {
    public static void main(String[] args) {
        DelayQueue<Task> queue = new DelayQueue<>();
        new Thread(new TaskProducer(queue), "Producer Thread").start();
        new Thread(new TaskConsumer(queue), "Consumer Thread").start();
    }
}

DelayQueue这个方案，每个消费者线程只需要等待所需要的时间差，因此响应速度更快。它内部用了一个优先队列，所以插入和删除的时间复杂度都是logn。

JDK里还有一个ScheduledThreadPoolExecutor，原理跟DelayQueue类似，封装的更完善，平时工作中可以用它，不过面试中，还是拿DelayQueue来讲吧，它封装得比较薄，容易讲清楚原理。

方案4: 时间轮(HashedWheelTimer)

时间轮(HashedWheelTimer)其实很简单，就是一个循环队列，如下图所示，

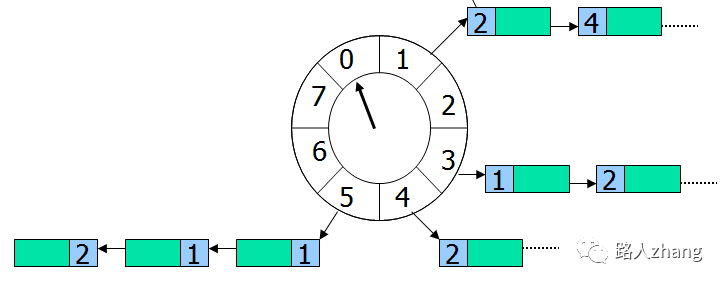
上图是一个长度为8的循环队列，假设该时间轮精度为秒，即每秒走一格，像手表那样，走完一圈就是8秒。每个格子指向一个任务集合，时间轮无限循环，每转到一个格子，就扫描该格子下面的所有任务，把时间到期的任务取出来执行。

举个例子，假设指针当前正指向格子0，来了一个任务需要4秒后执行，那么这个任务就会放在格子4下面，如果来了一个任务需要20秒后执行怎么？由于这个循环队列转一圈只需要8秒，这个任务需要多转2圈，所以这个任务的位置虽然依旧在格子4(20%8+0=4)下面，不过需要多转2圈后才执行。因此每个任务需要有一个字段记录需圈数，每转一圈就减1，减到0则立刻取出来执行。

怎么实现时间轮呢？Netty中已经有了一个时间轮的实现, HashedWheelTimer.java，可以参考它的源代码。

时间轮的优点是性能高，插入和删除的时间复杂度都是O(1)。Linux 内核中的定时器采用的就是这个方案。

Follow up: 如何设计一个分布式的定时任务调度器呢？ 答: Redis ZSet, RabbitMQ等

最近一个小时内访问频率最高的10个IP

实时输出最近一个小时内访问频率最高的10个IP，要求：

实时输出
从当前时间向前数的1个小时
QPS可能会达到10W/s

这道题乍一看很像Top K 频繁项，是不是需要 Lossy Count 或 Count-Min Sketch 之类的算法呢？

其实杀鸡焉用牛刀，这道题用不着上述算法，请听我仔细分析。

QPS是 10万/秒，即一秒内最高有 10万个请求，那么一个小时内就有，向上取整，大概是个请求，也不是很大。我们在内存中建立3600个HashMap<Int,Int>，放在一个数组里，每秒对应一个HashMap，IP地址为key, 出现次数作为value。这样，一个小时内最多有个pair，每个pair占8字节，总内存大概是节，即4GB，单机完全可以存下。
同时还要新建一个固定大小为10的小根堆，用于存放当前出现次数最大的10个IP。堆顶是10个IP里频率最小的IP。
每次来一个请求，就把该秒对应的HashMap里对应的IP计数器增1，并查询该IP是否已经在堆中存在，

如果不存在，则把该IP在3600个HashMap的计数器加起来，与堆顶IP的出现次数进行比较，如果大于堆顶元素，则替换掉堆顶元素，如果小于，则什么也不做
如果已经存在，则把堆中该IP的计数器也增1，并调整堆

4 . 需要有一个后台常驻线程，每过一秒，把最旧的那个HashMap销毁，并为当前这一秒新建一个HashMap，这样维持一个一小时的窗口。

5 . 每次查询top 10的IP地址时，把堆里10个IP地址返回来即可。

以上就是该方案的全部内容。

有的人问，可不可以用"IP + 时间"作为key, 把所有pair放在单个HashMap里？如果把所有数据放在一个HashMap里，有两个巨大的缺点，

第4步里，怎么淘汰掉一个小时前的pair呢？这时候后台线程只能每隔一秒，全量扫描这个HashMap里的所有pair,把过期数据删除，这是线性时间复杂度，很慢。
这时候HashMap里的key存放的是"IP + 时间"组合成的字符串，占用内存远远大于一个int。而前面的方案，不用存真正的时间，只需要开一个3600长度的数组来表示一个小时时间窗口。

key-Value存储引擎

请设计一个Key-Value存储引擎(Design a key-value store)。

这是一道频繁出现的题目，个人认为也是一道很好的题目，这题纵深非常深，内行的人可以讲的非常深。

首先讲两个术语，数据库和存储引擎。数据库往往是一个比较丰富完整的系统, 提供了SQL查询语言，事务和水平扩展等支持。然而存储引擎则是小而精, 纯粹专注于单机的读/写/存储。一般来说, 数据库底层往往会使用某种存储引擎。

目前开源的KV存储引擎中，RocksDB是流行的一个，MongoDB和MySQL底层可以切换成RocksDB， TiDB底层直接使用了RocksDB。大多数分布式数据库的底层不约而同的都选择了RocksDB。

RocksDB最初是从LevelDB进化而来的，我们先从简单一点的LevelDB入手，借鉴它的设计思路。

LevelDB整体结构

有一个反直觉的事情是，内存随机写甚至比硬盘的顺序读还要慢，磁盘随机写就更慢了，说明我们要避免随机写，最好设计成顺序写。因此好的KV存储引擎，都在尽量避免更新操作，把更新和删除操作转化为顺序写操作。LevelDB采用了一种SSTable的数据结构来达到这个目的。

SSTable(Sorted String Table)就是一组按照key排序好的 key-value对, key和value都是字节数组。SSTable既可以在内存中，也可以在硬盘中。SSTable底层使用LSM Tree(Log-Structured Merge Tree)来存放有序的key-value对。

LevelDB整体由如下几个组成部分，

MemTable。即内存中的SSTable，新数据会写入到这里，然后批量写入磁盘，以此提高写的吞吐量。
Log文件。写MemTable前会写Log文件，即用WAL(Write Ahead Log)方式记录日志，如果机器突然掉电，内存中的MemTable丢失了，还可以通过日志恢复数据。WAL日志是很多传统数据库例如MySQL采用的技术，详细解释可以参考数据库如何用 WAL 保证事务一致性？- 知乎专栏。
Immutable MemTable。内存中的MemTable达到指定的大小后，将不再接收新数据，同时会有新的MemTable产生，新数据写入到这个新的MemTable里，Immutable MemTable随后会写入硬盘，变成一个SST文件。
SSTable文件。即硬盘上的SSTable，文件尾部追加了一块索引，记录key->offset，提高随机读的效率。SST文件为Level 0到Level N多层，每一层包含多个SST文件；单个SST文件容量随层次增加成倍增长；Level0的SST文件由Immutable MemTable直接Dump产生，其他Level的SST文件由其上一层的文件和本层文件归并产生。
Manifest文件。Manifest文件中记录SST文件在不同Level的分布，单个SST文件的最大最小key，以及其他一些LevelDB需要的元信息。
Current文件。从上面的介绍可以看出，LevelDB启动时的首要任务就是找到当前的Manifest，而Manifest可能有多个。Current文件简单的记录了当前Manifest的文件名。

LevelDB的一些核心逻辑如下，

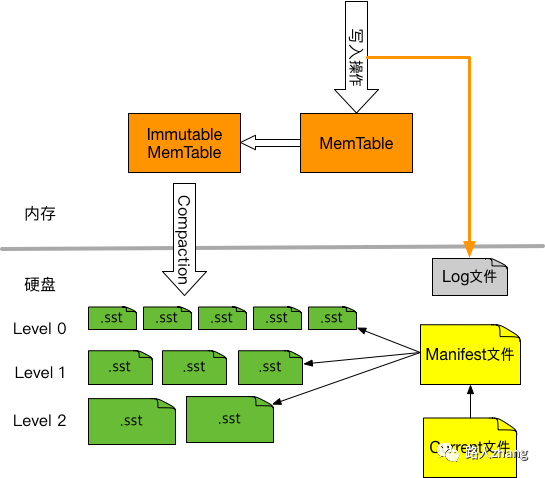
首先SST文件尾部的索引要放在内存中，这样读索引就不需要一次磁盘IO了
所有读要先查看MemTable，如果没有再查看内存中的索引
所有写操作只能写到MemTable, 因为SST文件不可修改
定期把Immutable MemTable写入硬盘，成为SSTable文件，同时新建一个MemTable会继续接收新来的写操作
定期对SSTable文件进行合并
由于硬盘上的SSTable文件是不可修改的，那怎么更新和删除数据呢？对于更新操作，追加一个新的key-value对到文件尾部，由于读SSTable文件是从前向后读的，所以新数据会最先被读到；对于删除操作，追加“墓碑”值(tombstone)，表示删除该key，在定期合并SSTable文件时丢弃这些key, 即可删除这些key。

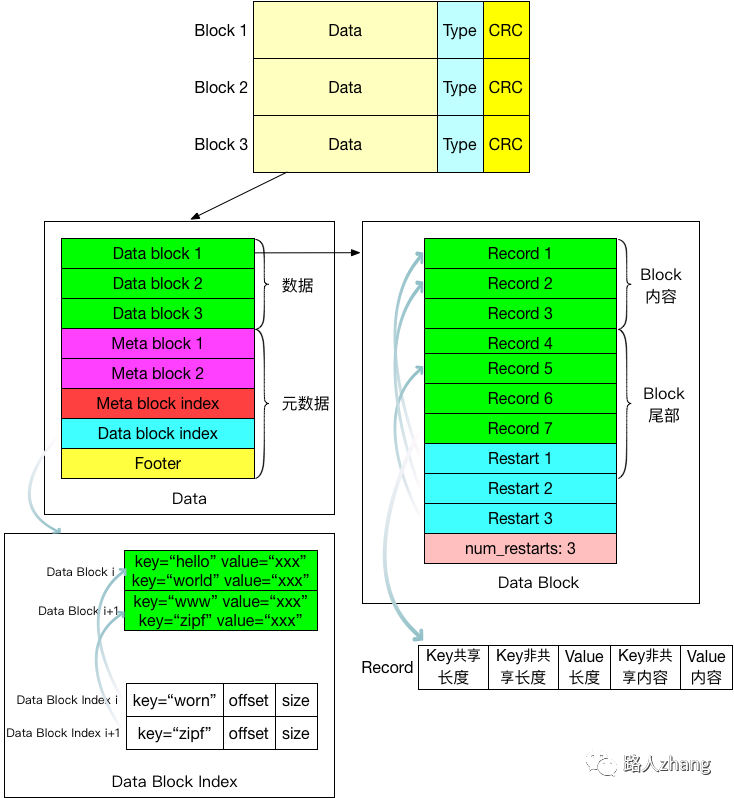
Manifest文件

Manifest文件记录各个SSTable各个文件的管理信息，比如该SST文件处于哪个Level，文件名称叫啥，最小key和最大key各自是多少，如下图所示，

Log文件

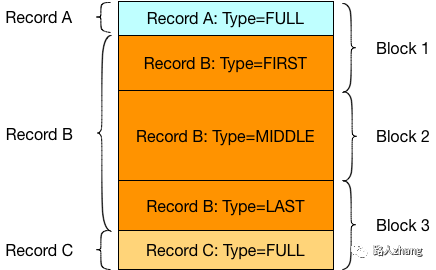
Log文件主要作用是系统发生故障时，能够保证不会丢失数据。因为在数据写入内存中的MemTable之前，会先写入Log文件，这样即使系统发生故障，MemTable中的数据没有来得及Dump到磁盘，LevelDB也可以根据log文件恢复内存中的MemTable，不会造成系统丢失数据。这个方式就叫做 WAL(Write Ahead Log)，很多传统数据库例如MySQL也使用了WAL技术来记录日志。

每个Log文件由多个block组成，每个block大小为32K，读取和写入以block为基本单位。下图所示的Log文件包含3个Block

SSTable

MemTable

MemTable 是内存中的数据结构，存储的内容跟硬盘上的SSTable一样，只是格式不一样。Immutable MemTable的内存结构和Memtable是完全一样的，区别仅仅在于它是只读的，而MemTable则是允许写入和读取的。当MemTable写入的数据占用内存到达指定大小，则自动转换为Immutable Memtable，等待Dump到磁盘中，系统会自动生成一个新的MemTable供写操作写入新数据，理解了MemTable，那么Immutable MemTable自然不在话下。

MemTable里的数据是按照key有序的，因此当插入新数据时，需要把这个key-value对插入到合适的位置上，以保持key有序性。MemTable底层的核心数据结构是一个跳表(Skip List)。跳表是红黑树的一种替代数据结构，具有更高的写入速度，而且实现起来更加简单，请参考跳表(Skip List)。

前面我们介绍了LevelDB的一些内存数据结构和文件，这里开始介绍一些动态操作，例如读取，写入，更新和删除数据，分层合并，错误恢复等操作。

添加、更新和删除数据

LevelDB写入新数据时，具体分为两个步骤：

将这个操作顺序追加到log文件末尾。尽管这是一个磁盘操作，但是文件的顺序写入效率还是很高的，所以不会降低写入的速度
如果log文件写入成功，那么将这条key-value记录插入到内存中MemTable。

LevelDB更新一条记录时，并不会本地修改SST文件，而是会作为一条新数据写入MemTable，随后会写入SST文件，在SST文件合并过程中，新数据会处于文件尾部，而读取操作是从文件尾部倒着开始读的，所以新值一定会最先被读到。

LevelDB删除一条记录时，也不会修改SST文件，而是用一个特殊值(墓碑值，tombstone)作为value，将这个key-value对追加到SST文件尾部，在SST文件合并过程中，这种值的key都会被忽略掉。

核心思想就是把写操作转换为顺序追加，从而提高了写的效率。

读取数据

读操作使用了如下几个手段进行优化：

MemTable + SkipList
Binary Search(通过 manifest 文件)
页缓存
bloom filter
周期性分层合并

数据流采样

有一个无限的整数数据流，如何从中随机地抽取k个整数出来？

这是一个经典的数据流采样问题，我们一步一步来分析。

当k=1时

我们先考虑最简单的情况，k=1，即只需要随机抽取一个样本出来。抽样方法如下：

当第一个整数到达时，保存该整数
当第2个整数到达时，以1/2的概率使用该整数替换第1个整数，以1/2的概率丢弃改整数
当第i个整数到达时，以的概率使用第i个整数替换被选中的整数，以的概率丢弃第i个整数

假设数据流目前已经流出共n个整数，这个方法能保证每个元素被选中的概率是

吗？用数学归纳法，证明如下：1. 当n=1时，由于是第1个数，被选中的概率是100%，命题成立 2. 假设当n=m(m>=1)时，命题成立，即前m个数，每一个被选中的概率是 3. 当n=m+1时，第m+1个数被选中的概率是 , 前m个数被选中的概率是，命题依然成立

由1，2，3知n>=1时命题成立，证毕。

当k>1时

当 k > 1，需要随机采样多个样本时，方法跟上面很类似，

前k个整数到达时，全部保留，即被选中的概率是 100%，
第i个整数到达时，以的概率替换k个数中的某一个，以的概率丢弃，保留k个数不变

假设数据流目前已经流出共N个整数，这个方法能保证每个元素被选中的概率是

吗？用数学归纳法，证明如下：1. 当n=m(m<=k)时，被选中的概率是100%，命题成立 2. 假设当n=m(m>k)时，命题成立，即前m个数，每一个被选中的概率是 3. 当n=m+1时，第m+1个数被选中的概率是 , 前m个数被选中的概率是，命题依然成立

由1，2，3知n>=1时命题成立，证毕。

基数估计

如何计算数据流中不同元素的个数？例如，独立访客(Unique Visitor，简称UV)统计。这个问题称为基数估计(Cardinality Estimation)，也是一个很经典的题目。

方案1: HashSet

首先最容易想到的办法是用HashSet，每来一个元素，就往里面塞，HashSet的大小就所求答案。但是在大数据的场景下，HashSet在单机内存中存不下。

方案2: bitmap

HashSet耗内存主要是由于存储了元素的真实值，可不可以不存储元素本身呢？bitmap就是这样一个方案，假设已经知道不同元素的个数的上限，即基数的最大值，设为N，则开一个长度为N的bit数组，地位跟HashSet一样。每个元素与bit数组的某一位一一对应，该位为1，表示此元素在集合中，为0表示不在集合中。那么bitmap中1的个数就是所求答案。

这个方案的缺点是，bitmap的长度与实际的基数无关，而是与基数的上限有关。假如要计算上限为1亿的基数，则需要12.5MB的bitmap，十个网站就需要125M。关键在于，这个内存使用与集合元素数量无关，即使一个网站仅仅有一个1UV，也要为其分配12.5MB内存。该算法的空间复杂度是O(N_{max})O(Nma**x)。

实际上目前还没有发现在大数据场景中准确计算基数的高效算法，因此在不追求绝对准确的情况下，使用近似算法算是一个不错的解决方案。

方案3: Linear Counting

Linear Counting的基本思路是：

选择一个哈希函数h，其结果服从均匀分布
开一个长度为m的bitmap，均初始化为0(m设为多大后面有讨论)
数据流每来一个元素，计算其哈希值并对m取模，然后将该位置为1
查询时，设bitmap中还有u个bit为0，则不同元素的总数近似为

在使用Linear Counting算法时，主要需要考虑的是bitmap长度m。m主要由两个因素决定，基数大小以及容许的误差。假设基数大约为n，允许的误差为ϵ，则m需要满足如下约束，

, 其中精度越高，需要的m越大。

Linear Counting 与方案1中的bitmap很类似，只是改善了bitmap的内存占用，但并没有完全解决，例如一个网站只有一个UV，依然要为其分配m位的bitmap。该算法的空间复杂度与方案2一样，依然是

。

方案4: LogLog Counting

LogLog Counting的算法流程：

1 . 均匀随机化。选取一个哈希函数h应用于所有元素，然后对哈希后的值进行基数估计。哈希函数h必须满足如下条件，

a . 哈希碰撞可以忽略不计。哈希函数h要尽可能的减少冲突

b . h的结果是均匀分布的。也就是说无论原始数据的分布如何，其哈希后的结果几乎服从均匀分布（完全服从均匀分布是不可能的，D. Knuth已经证明不可能通过一个哈希函数将一组不服从均匀分布的数据映射为绝对均匀分布，但是很多哈希函数可以生成几乎服从均匀分布的结果，这里我们忽略这种理论上的差异，认为哈希结果就是服从均匀分布）。 c . 哈希后的结果是固定长度的

2 . 对于元素计算出哈希值，由于每个哈希值是等长的，令长度为L

3 . 对每个哈希值，从高到低找到第一个1出现的位置，取这个位置的最大值，设为p，则基数约等于

如果直接使用上面的单一估计量进行基数估计会由于偶然性而存在较大误差。因此，LLC采用了分桶平均的思想来降低误差。具体来说，就是将哈希空间平均分成m份，每份称之为一个桶（bucket）。对于每一个元素，其哈希值的前k比特作为桶编号，其中

，而后L-k个比特作为真正用于基数估计的比特串。桶编号相同的元素被分配到同一个桶，在进行基数估计时，首先计算每个桶内最大的第一个1的位置，设为p[i]，然后对这m个值取平均后再进行估计，即基数的估计值为。这相当于做多次实验然后去平均值，可以有效降低因偶然因素带来的误差。LogLog Counting 的空间复杂度仅有

，内存占用极少，这是它的优点。不过LLC也有自己的缺点，当基数不是很大的时候，误差比较大。关于该算法的数学证明，请阅读原始论文和参考资料里的链接，这里不再赘述。

方案5: HyperLogLog Counting

HyperLogLog Counting（以下简称HLLC）的基本思想是在LLC的基础上做改进，

第1个改进是使用调和平均数替代几何平均数，调和平均数可以有效抵抗离群值的扰。注意LLC是对各个桶取算术平均数，而算术平均数最终被应用到2的指数上，所以总体来看LLC取的是几何平均数。由于几何平均数对于离群值（例如0）特别敏感，因此当存在离群值时，LLC的偏差就会很大，这也从另一个角度解释了为什么基数n不太大时LLC的效果不太好。这是因为n较小时，可能存在较多空桶，这些特殊的离群值干扰了几何平均数的稳定性。使用调和平均数后，估计公式变为，其中
第2个改进是加入了分段偏差修正。具体来说，设e为基数的估计值，
当时，使用 Linear Counting
当时，使用 HyperLogLog Counting
当时，修改估计公式为

关于分段偏差修正的效果分析也可以在原论文中找到。

频率估计

如何计算数据流中任意元素的频率？

这个问题也是大数据场景下的一个经典问题，称为频率估计(Frequency Estimation)问题。

方案1: HashMap

用一个HashMap记录每个元素的出现次数，每来一个元素，就把相应的计数器增1。这个方法在大数据的场景下不可行，因为元素太多，单机内存无法存下这个巨大的HashMap。

方案2: 数据分片 + HashMap

既然单机内存存不下所有元素，一个很自然的改进就是使用多台机器。假设有8台机器，每台机器都有一个HashMap，第1台机器只处理hash(elem)%8==0的元素，第2台机器只处理hash(elem)%8==1的元素，以此类推。查询的时候，先计算这个元素在哪台机器上，然后去那台机器上的HashMap里取出计数器。

方案2能够scale, 但是依旧是把所有元素都存了下来，代价比较高。

如果允许近似计算，那么有很多高效的近似算法，单机就可以处理海量的数据。下面讲几个经典的近似算法。

方案3: Count-Min Sketch

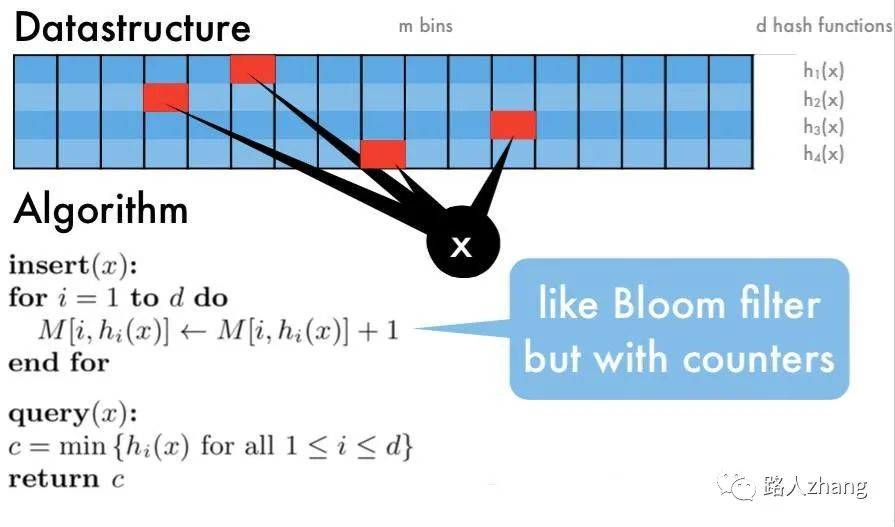
Count-Min Sketch 算法流程：

选定d个hash函数，开一个 dxm 的二维整数数组作为哈希表
对于每个元素，分别使用d个hash函数计算相应的哈希值，并对m取余，然后在对应的位置上增1，二维数组中的每个整数称为sketch
要查询某个元素的频率时，只需要取出d个sketch, 返回最小的那一个（其实d个sketch都是该元素的近似频率，返回任意一个都可以，该算法选择最小的那个）

这个方法的思路和 Bloom Filter 比较类似，都是用多个hash函数来降低冲突。

空间复杂度O(dm)。Count-Min Sketch 需要开一个 dxm 大小的二位数组，所以空间复杂度是O(dm)
时间复杂度O(n)。Count-Min Sketch 只需要一遍扫描，所以时间复杂度是O(n)

Count-Min Sketch算法的优点是省内存，缺点是对于出现次数比较少的元素，准确性很差，因为二维数组相比于原始数据来说还是太小，hash冲突比较严重，导致结果偏差比较大。

方案4: Count-Mean-Min Sketch

Count-Min Sketch算法对于低频的元素，结果不太准确，主要是因为hash冲突比较严重，产生了噪音，例如当m=20时，有1000个数hash到这个20桶，平均每个桶会收到50个数，这50个数的频率重叠在一块了。Count-Mean-Min Sketch 算法做了如下改进：

来了一个查询，按照 Count-Min Sketch的正常流程，取出它的d个sketch
对于每个hash函数，估算出一个噪音，噪音等于该行所有整数(除了被查询的这个元素)的平均值
用该行的sketch 减去该行的噪音，作为真正的sketch
返回d个sketch的中位数

class CountMeanMinSketch {
    // initialization and addition procedures as in CountMinSketch
    // n is total number of added elements
    long estimateFrequency(value) {
        long e[] = new long[d]
        for(i = 0; i < d; i++) {
            sketchCounter = estimators[i][ hash(value, i) ]
            noiseEstimation = (n - sketchCounter) / (m - 1)
            e[i] = sketchCounter – noiseEstimator
        }
        return median(e)
    }
}

Count-Mean-Min Sketch算法能够显著的改善在长尾数据上的精确度。

Top k频繁项

寻找数据流中出现最频繁的k个元素(find top k frequent items in a data stream)。这个问题也称为 Heavy Hitters.

这题也是从实践中提炼而来的，例如搜索引擎的热搜榜，找出访问网站次数最多的前10个IP地址，等等。

方案1: HashMap + Heap

用一个 HashMap<String, Long>，存放所有元素出现的次数，用一个小根堆，容量为k，存放目前出现过的最频繁的k个元素，

每次从数据流来一个元素，如果在HashMap里已存在，则把对应的计数器增1，如果不存在，则插入，计数器初始化为1
在堆里查找该元素，如果找到，把堆里的计数器也增1，并调整堆；如果没有找到，把这个元素的次数跟堆顶元素比较，如果大于堆丁元素的出现次数，则把堆丁元素替换为该元素，并调整堆
空间复杂度O(n)。HashMap需要存放下所有元素，需要O(n)的空间，堆需要存放k个元素，需要O(k)的空间，跟O(n)相比可以忽略不急，总的时间复杂度是O(n)
时间复杂度O(n)。每次来一个新元素，需要在HashMap里查找一下，需要O(1)的时间；然后要在堆里查找一下，O(k)的时间，有可能需要调堆，又需要O(logk)的时间，总的时间复杂度是O(n(k+logk))，k是常量，所以可以看做是O(n)。

如果元素数量巨大，单机内存存不下，怎么办？有两个办法，见方案2和3。

方案2: 多机HashMap + Heap

可以把数据进行分片。假设有8台机器，第1台机器只处理hash(elem)%8==0的元素，第2台机器只处理hash(elem)%8==1的元素，以此类推。
每台机器都有一个HashMap和一个 Heap, 各自独立计算出 top k 的元素
把每台机器的Heap，通过网络汇总到一台机器上，将多个Heap合并成一个Heap，就可以计算出总的 top k 个元素了

方案3: Count-Min Sketch + Heap

既然方案1中的HashMap太大，内存装不小，那么可以用Count-Min Sketch算法代替HashMap，

在数据流不断流入的过程中，维护一个标准的Count-Min Sketch 二维数组
维护一个小根堆，容量为k
每次来一个新元素，
将相应的sketch增1
在堆中查找该元素，如果找到，把堆里的计数器也增1，并调整堆；如果没有找到，把这个元素的sketch作为钙元素的频率的近似值，跟堆顶元素比较，如果大于堆丁元素的频率，则把堆丁元素替换为该元素，并调整堆

这个方法的时间复杂度和空间复杂度如下：

空间复杂度O(dm)。m是二维数组的列数，d是二维数组的行数，堆需要O(k)的空间，不过k通常很小，堆的空间可以忽略不计
时间复杂度O(nlogk)。每次来一个新元素，需要在二维数组里查找一下，需要O(1)的时间；然后要在堆里查找一下，O(logk)的时间，有可能需要调堆，又需要O(logk)的时间，总的时间复杂度是O(nlogk)。

方案4: Lossy Counting

Lossy Couting 算法流程：

建立一个HashMap，用于存放每个元素的出现次数
建立一个窗口（窗口的大小由错误率决定，后面具体讨论）
等待数据流不断流进这个窗口，直到窗口满了，开始统计每个元素出现的频率，统计结束后，每个元素的频率减1，然后将出现次数为0的元素从HashMap中删除
返回第2步，不断循环

Lossy Counting 背后朴素的思想是，出现频率高的元素，不太可能减一后变成0，如果某个元素在某个窗口内降到了0，说明它不太可能是高频元素，可以不再跟踪它的计数器了。随着处理的窗口越来越多，HashMap也会不断增长，同时HashMap里的低频元素会被清理出去，这样内存占用会保持在一个很低的水平。

很显然，Lossy Counting 算法是个近似算法，但它的错误率是可以在数学上证明它的边界的。假设要求错误率不大于ε，那么窗口大小为1/ε，对于长度为N的流，有N／（1/ε）＝εN 个窗口，由于每个窗口结束时减一了，那么频率最多被少计数了窗口个数εN。

该算法只需要一遍扫描，所以时间复杂度是O(n)。

该算法的内存占用，主要在于那个HashMap, Gurmeet Singh Manku 在他的论文里，证明了HashMap里最多有 1/ε log (εN)个元素，所以空间复杂度是O(1/ε log (εN))。

范围查询

给定一个无限的整数数据流，如何查询在某个范围内的元素出现的总次数？例如数据库常常需要SELECT count(v) WHERE v >= l AND v < u。这个经典的问题称为范围查询(Range Query)。

方案1: Array of Count-Min Sketches

有一个简单方法，既然Count-Min Sketch可以计算每个元素的频率，那么我们把指定范围内所有元素的sketch加起来，不就是这个范围内元素出现的总数了吗？要注意，由于每个sketch都是近似值，多个近似值相加，误差会被放大，所以这个方法不可行。

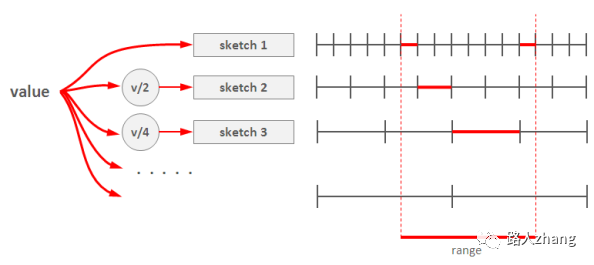
解决的办法就是使用多个“分辨率”不同的Count-Min Sketch。第1个sketch每个格子存放单个元素的频率，第2个sketch每个格子存放2个元素的频率（做法很简答，把该元素的哈希值的最低位bit去掉，即右移一位，等价于除以2，再继续后续流程），第3个sketch每个格子存放4个元素的频率（哈希值右移2位即可），以此类推，最后一个sketch有2个格子，每个格子存放一半元素的频率总数，即第1个格子存放最高bit为0的元素的总次数，第2个格子存放最高bit为1的元素的总次数。Sketch的个数约等于log(不同元素的总数)。

插入元素时，算法伪代码如下，

def insert(x):
    for i in range(1, d+1):
        M1[i][h[i](x)] += 1
        M2[i][h[i](x)/2] += 1
        M3[i][h[i](x)/4] += 1
        M4[i][h[i](x)/8] += 1
        # ...

查询范围[l, u)时，从粗粒度到细粒度，找到多个区间，能够不重不漏完整覆盖区间[l, u)，将这些sketch的值加起来，就是该范围内的元素总数。举个例子，给定某个范围，如下图所示，最粗粒度的那个sketch里找不到一个格子，就往细粒度找，最后找到第1个sketch的2个格子，第2个sketch的1个格子和第3个sketch的1个格子，共4个格子，能够不重不漏的覆盖整个范围，把4个红线部分的值加起来就是所求结果

成员查询

给定一个无限的数据流和一个有限集合，如何判断数据流中的元素是否在这个集合中？

在实践中，我们经常需要判断一个元素是否在一个集合中，例如垃圾邮件过滤，爬虫的网址去重，等等。这题也是一道很经典的题目，称为成员查询(Membership Query)。

答案: Bloom Filter