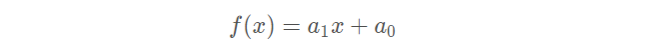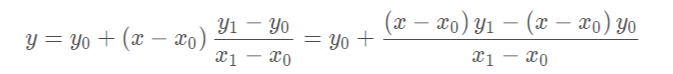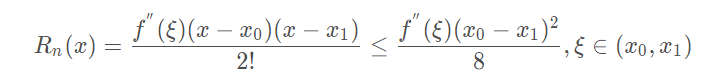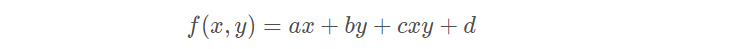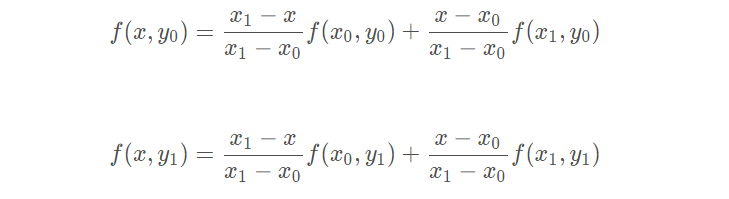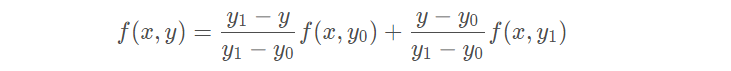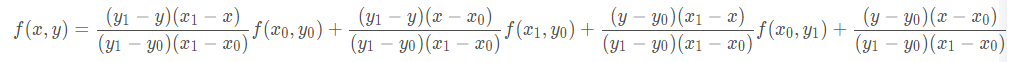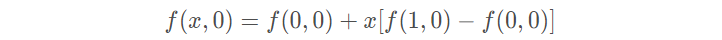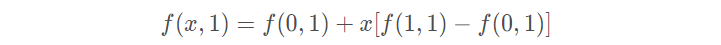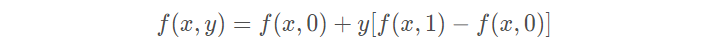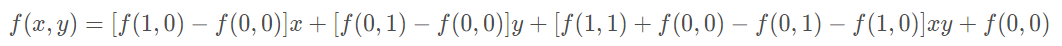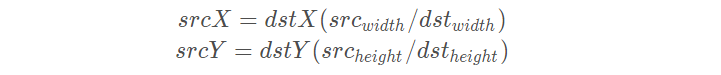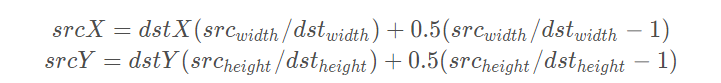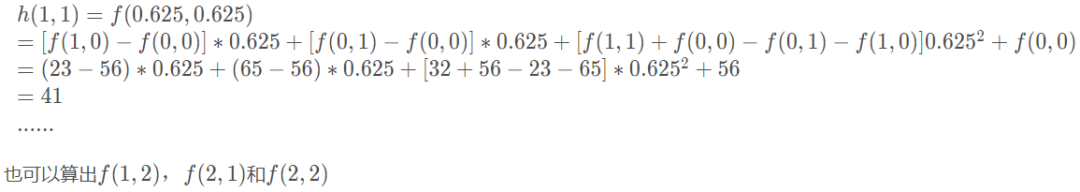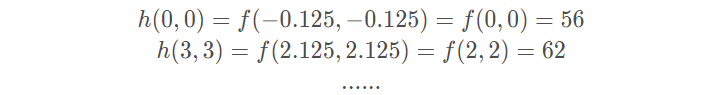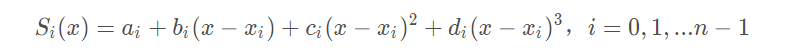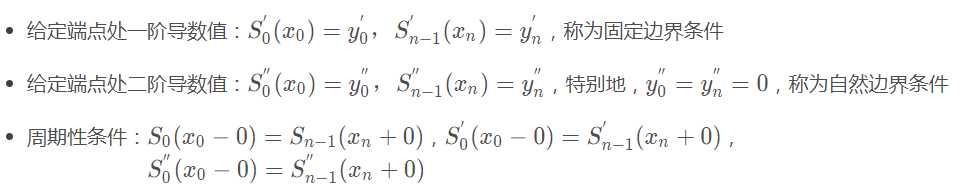来聊聊图像插值算法

本文转载自：AI算法修炼营

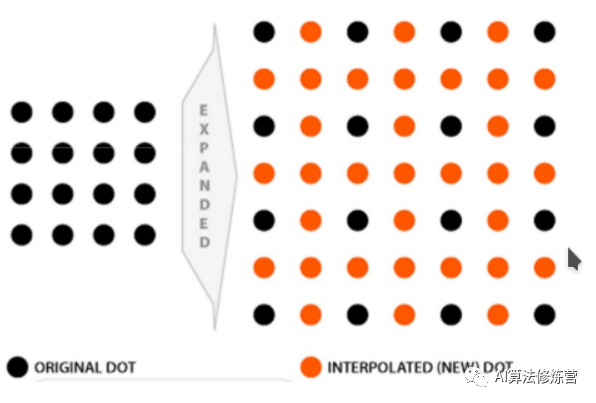
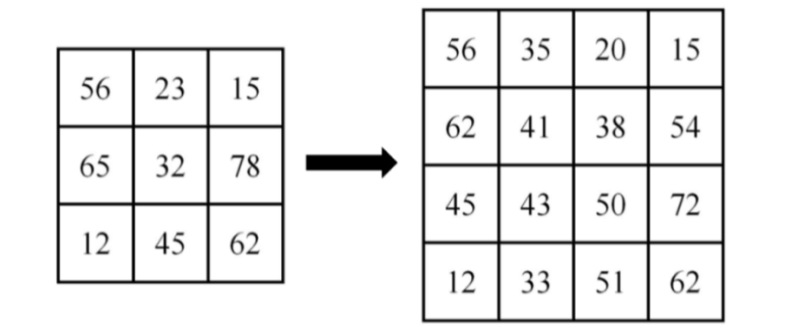
在图像几何变换时，无法给有些像素点直接赋值，例如将图像放大两倍，必然会多出一些无法被直接映射的像素点，对于这些像素点，通过插值决定它们的。于是，产生了图像插值算法。

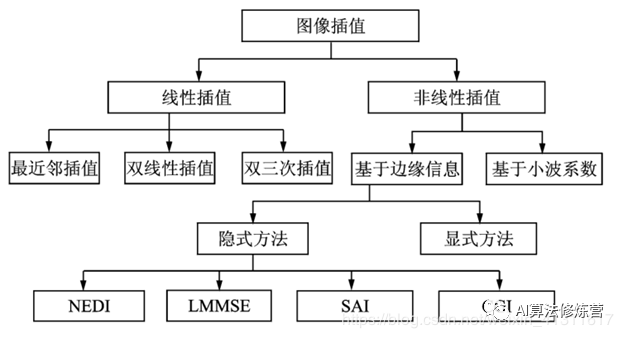
图像插值算法分类

主要可以分为两类，一类是线性图像插值方法，另一类是非线性图像插值方法，如上图所示。

传统的插值方法如最近邻插值，双线性插值以及双三次插值等都属于线性插值方法。这类插值方法在图像插值过程中采用同一种插值内核，不用考虑待插像素点所处的位置，这种做法会使图像中的边缘变得模糊不清，达不到高清图像的视觉效果。

非线性插值方法主要包括：基于小波系数的方法基于边缘信息的方法。其中，基于边缘信息的方法又可分为隐式方法和显式方法两种。隐式方法包含边缘导向插值(New edge directive interpolation，NEDI)，最小均方误差估计插值(Linear minimum mean square-error estimation，LMMSE)、软判决自适应插值(Soft-decision adaptive interpolation interpolation,SAI)，提出的边缘对比度引导的图像插值(Contrast-guideed image interpolation,CGI)等都是隐式的基于图像边缘的插值方法。

最新发展的话有基于决策树，深度学习，字典学习的图像插值算法。

线性插值算法

线性插值算法常用有五种，在OpenCV中设置可以通过相关参数很方便地进行设置。

线性插值：使用连接两个已知量的直线来确定在这两个已知量之间的一个未知量的值。线性插值形式：

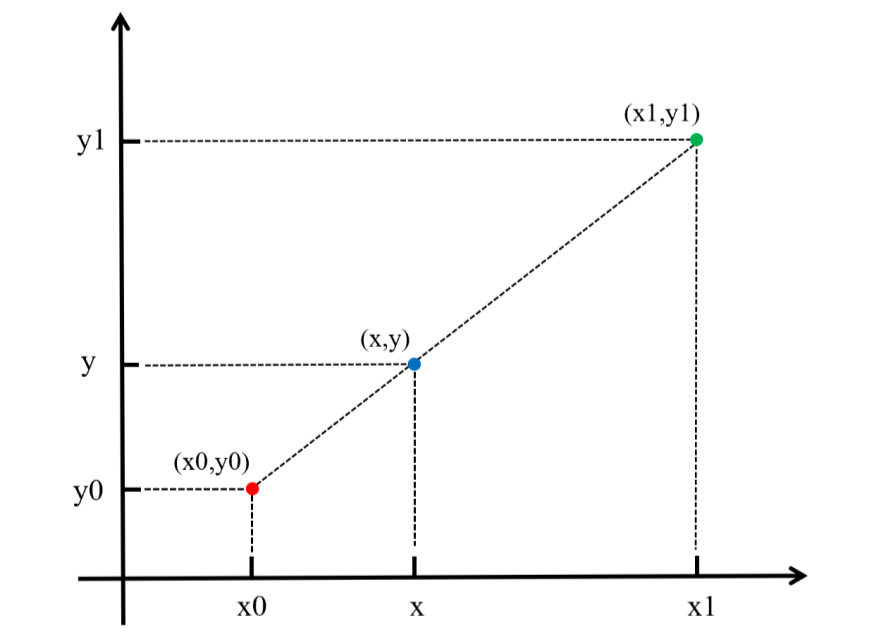
如下图所示：

线性插值多项式：

其实，即使x不在x0到x1之间，这个公式也是成立的。在这种情况下，这种方法叫作线性外插。

线性插值的误差：线性插值其实就是拉格朗日插值有2个结点时的情况。插值余项为：

从插值余项可以看出，随着二阶导数的增大，线性插值的误差增大。即函数的曲率越大，线性插值近似的误差也越大。

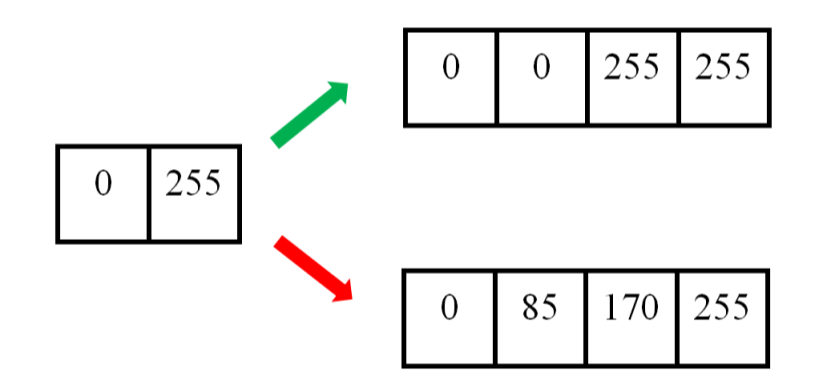
举个例子。下图中，左边为原图像，拉伸后，理想的输出图像的像素分布应该为绿色箭头指向的，但是按照线性插值，会得到红色箭头指向的结果。

一、最近邻插值算法 INTER_NEAREST

在一维空间中，最近点插值就相当于四舍五入取整。在二维图像中，像素点的坐标都是整数，该方法就是选取离目标点最近的点。会在一定程度上损失 空间对称性（Alignment），在 RoI Pooling 中使用。

具体来说，将目标图像中的点，对应到原图像中后，找到最相邻的整数坐标点的像素值，作为该点的像素值输出。

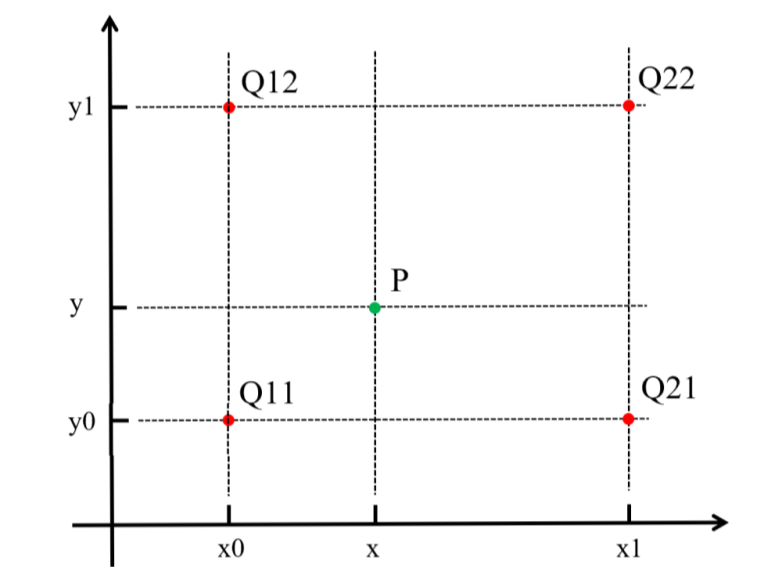
如上图所示，目标图像中的某点投影到原图像中的位置为点P，与P距离最近的点为Q11，此时易知，f(P)=f(Q11)。

如果距离四个点都相等（中心处）要如何处理？

由最邻近插值法，放大后的图像有很严重的马赛克，会出现明显的块状效应；缩小后的图像有很严重的失真。这是一种最基本、最简单的图像缩放方式。变换后的每个像素点的像素值，只由原图像中的一个像素点确定。例如上面，点(0,0.75)的像素只由(0,1)确定，这样的效果显然不好。点(0,0.75)的像素不止和(0,1)有关，和(0,0)也有关，只是(0,1)的影响更大。如果可以用附近的几个像素点按权重分配，共同确定目标图像某点的像素，效果会更好。下面的双线性插值就解决了这个问题。

二、双线性插值算法 （默认） INTER_LINEAR

双线性插值形式：

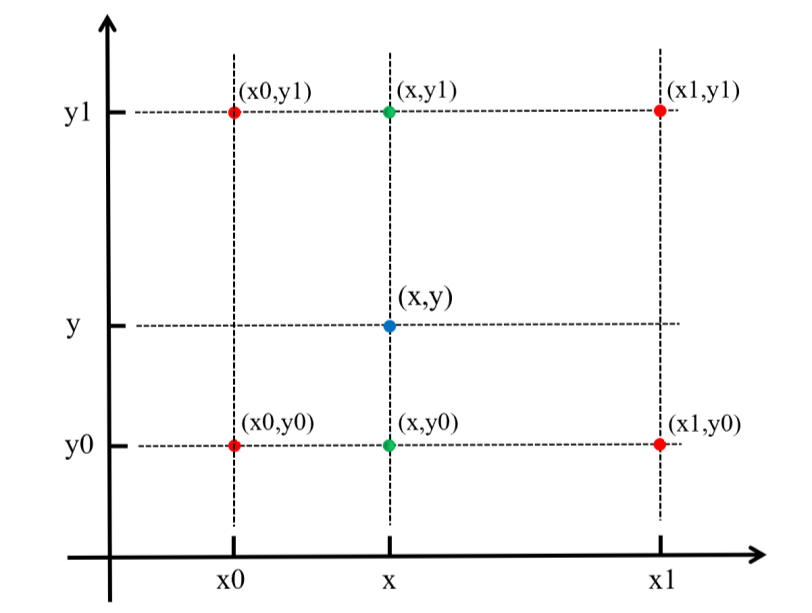
双线性插值是线性插值在二维时的推广,在两个方向上共做了三次线性插值。定义了一个双曲抛物面与四个已知点拟合。具体操作为在X方向上进行两次线性插值计算，然后在Y方向上进行一次插值计算。如下图所示：

首先，f(x,y)为二元函数，假设我们知道f(x0,y0),f(x1,y1),f(x0,y1),f(x1,y0)四个点的值。这四个点确定一个矩形，我们希望通过插值得到矩形内任意点的函数值。

先在x方向上进行两次线性插值，得到：

再在y方向上进行一次线性插值，得到：

综合起来，就是双线性插值的结果：

如果选择一个坐标系统，使f(x)已知的四个点的坐标分别为(0,0),(0,1),(1,0),(1,1)，那么确定一个单位正方形，四个点分别为正方形的四个顶点：

• 首先对上端的两个顶点进行线性插值得：

• 再对底端的两个顶点进行线性插值得：

• 最后，做垂直方向的线性插值，以确定：

• 整理得插值公式的化简形式：

原图像和目标图像的几何中心对齐

在计算目标图像中，对应原图像的虚拟坐标点时，一般的变换是：

这种变换下，原图像的有些点没有参与计算。举个例子，把9∗9的原图像缩小成3∗3，原图像的原点(0,0)和目标图像的原点(0,0)都为左上角，目标图像右上角的坐标为(0,2)，对应原图像的坐标为(0∗(9/3),2∗(9/3))=(0,6)。目标图像右边已经没有点了，(0,6)右边的像素点也就用不到了。

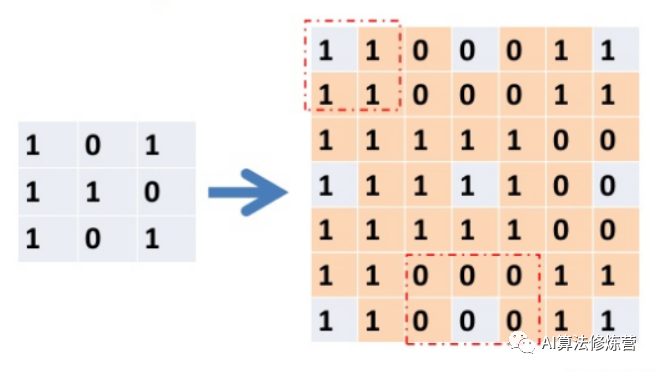
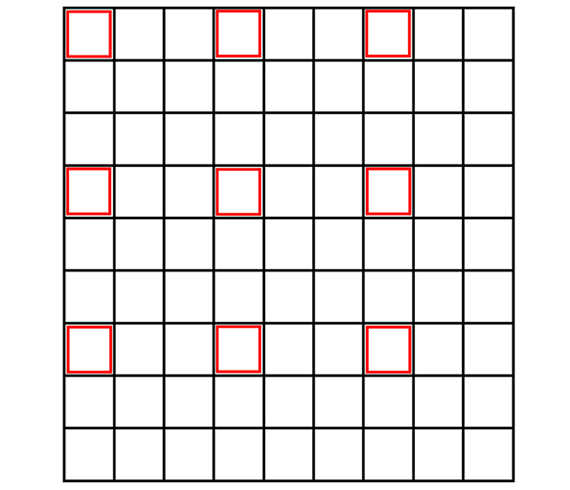
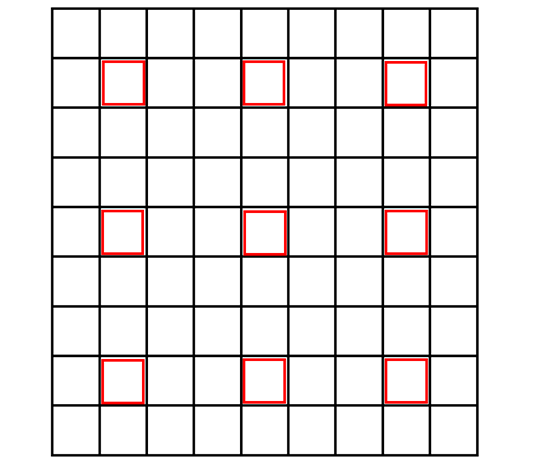
原图像和目标图像的像素之间的对应关系如下：

从图片可以看出，只有圈出来的红色部分参与运算了。目标图像的每个像素点的灰度值相对于原图像偏左上方，右下角的元素实际上没有参与运算。

为了让原图像和目标图像的中心对齐，我们规定另外一种变换方式：

就是在原来的变换后面加了调节因子：

0.5(src_width/dst_width−1)

这种变换下，目标图像的中心点(1,1)，对应了原图像的中心点(4,4)，两个图像的几何中心重合，能充分利用原图像的点，并且目标图像的每个像素点之间都是等间隔的，也都和两边有一定的边距。实际上，在openCv中也是这种变换方式。

cv.resize()的计算过程

对于缩小图像，目标图像中每个点都能找到原图像中包围它的四个临近点，每个点都进行双线性插值即可。

对于放大图像，边界附近的点经过坐标变换可能超出了原图像的范围。举个例子，把3∗3的原图像放大成4∗4。

• 中间的点：双线性插值

中间的点都能在原图像中找到包围它的四个临近点，做双线性插值即可。

• 边界上的点（除了顶点）：线性插值

例如，目标图像中的点(1,3)，对应原图像的点为(0.625,2.125)，原图像的纵坐标最大为2，找不到包围(0.625,2.125)四个点，所以用它最邻近的两个点(0,2)和(1,2)做线性插值（外插），得到目标图像中(1,3)的像素值。

• 四个顶点：最邻近插值

例如，目标图像右上角的顶点(0,3)，对于原图像的点为(0,2.125)，直接用原图像右上角的顶点(0,2)作为它的值即可。

计算过程：

用h(x,y)表示目标图像，f(x,y)表示原图像

• 中间的点：双线性插值

• 边界上的点（除了顶点）：线性插值

• 四个顶点：最邻近插值

三、三次样条插值算法 INTER_CUBIC

给定n+1个点，a=x_0<x_1<...<x_n=b，以及他们的函数值f(x_i)，i=0,1,2,...n上，确定一个三次多项式：

每个三次多项式中有四个未知参数，有n个区间，n个多项式，共4n个未知参数。我们知道“n个未知数需要n个已知条件确定唯一解”，所以要确定这4n个未知参数，共需要4n个已知条件。

每个三次多项式满足如下条件：

以上共4n−2个条件，还差2个条件，由如下三种边界条件确定：

4n个条件有了，就可以确定每个区间上的三次多项式。对于每个区间内的点，就可以用Si(x)得到插值结果。三次样条插值具有良好的收敛性，稳定性和光滑性，优点明显，是非常重要的插值工具。

非线性插值算法

非线性插值算法主要有两大类，基于小波变换的插值算法，基于边缘信息的插值算法。

一、基于小波变换的插值算法

由于小波具有多分辨率分析功能和逐渐局部细化等性质，基于小波 的 插 值 方 法也 相 继 被 提 出。小 波 变 换 (ＤＷＴ)的基本思想就是将信号分解到不同的尺度或者分辨率层上，这样可以在不同的尺度上独立的对信号进行研究和分析。

正交小波分解不仅可将图像的高低频信息很好地分离，而且分解后各层子带之间具有相似性。分解后的低频信息中包含了图像的绝大部分能量；高频信息则对应图像的边缘信息。

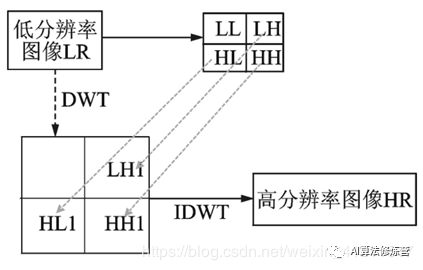
如下图所示，通过小波变换，将图像的高低频信息分离后，可以单独对高频信息进行处理。若能准确地得到图像的高频细节，利用重构理论，将得到的高频与原有的低频相叠加，再通过离散小波逆变换就可以得到分辨率高一倍的图像。

二、基于边缘信息的插值

由于边缘对人眼知觉系统的视觉重要性，有研究者提出了边缘引导的图像插值方法来对图像边缘进行放大。

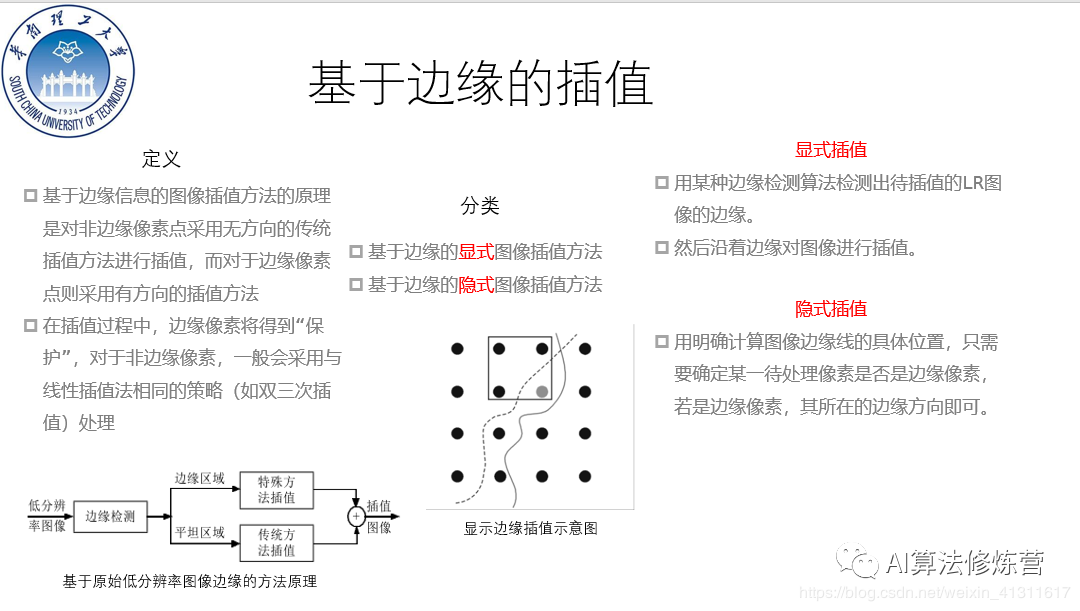
基于边缘信息的图像插值方法的核心思想是对非边缘像素点采用无方向的传统插值方法进行插值，而对于边缘像素点则采用有方向的插值方法。边缘像素及其方向判断的精准度对最后的图像插值结果有着决定性的影响。

上图给出的是显式边缘插值算法的示意图，其中黑色虚线是图像的真实边缘，灰色实线是边缘检测算法检测出的边缘。对于图中的灰色像素点的插值，需要确定其在边缘的哪一侧，然后利用该侧的已知像素点对其进行估算。由于图像边缘的连续性与数字图像离散性的冲突，将连续的边缘映射到离散的像素点上会产生较大的误差，而且沿着图像边缘插值不易实现，所以此类方法发展较慢。

隐式边缘插值算法中的CGI算法

CGI又叫边缘对比度引导的图像插值(Contrast-guideed image interpolation)

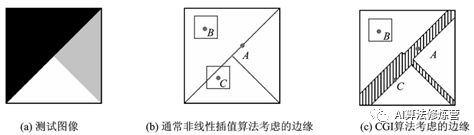
线性插值方法中，仅对传统意义上1-2个像素宽的边缘进行“保护”不够，为了保证插值效果，需要同时考虑距离边缘一定范围内的非边缘像素并对它们进行类似的保护（如采用边缘导向的一维方向插值，而不是采用无方向的二维插值），这一做法可称为“边缘扩散”或“边缘带状化”。特别地，边缘扩散的程度与边缘对比度（即边缘两侧像素的灰度值差异）成正比，即边缘对比度越大，扩散后的带状化边缘越宽。

参考

[1] 《一文讲解图像插值算法原理！附Python实现》

[2] https://blog.csdn.net/wonengguwozai/article/details/96107106

[3] https://blog.csdn.net/weixin_41311617/article/details/88943092

作者：姚童 | 公众号：Datawhale