漫画:什么是红黑树?(下篇)
作者 | 小灰 来源 | 程序员小灰(ID:chengxuyuanxiaohui)
上周,我们初步介绍了红黑树存在的意义,以及红黑树的插入操作,没看过的小伙伴可以点击下面链接:
今天,我们来继续介绍红黑树的删除操作,以及红黑树和其他平衡二叉树的比较。


二叉查找树是如何进行删除操作的呢?可以分成三种情况。
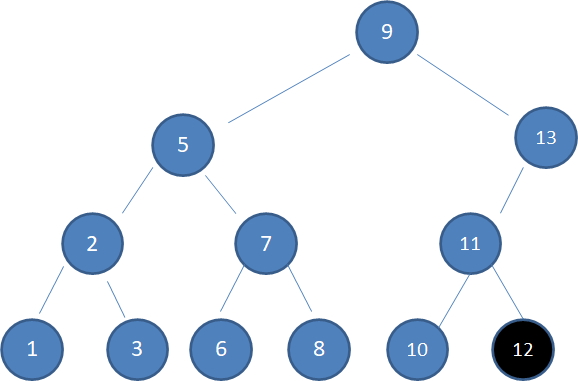
情况1,待删除的结点没有子结点:
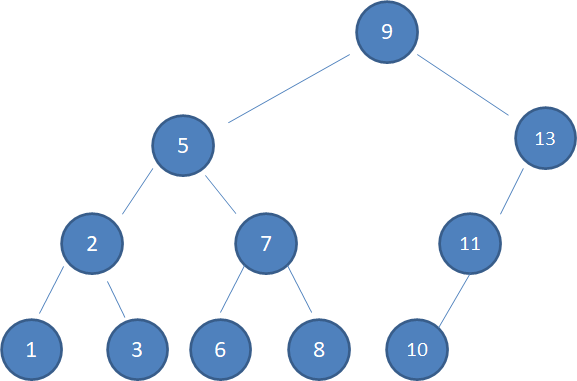
上图中,待删除的结点12是叶子结点,没有孩子,因此直接删除即可:
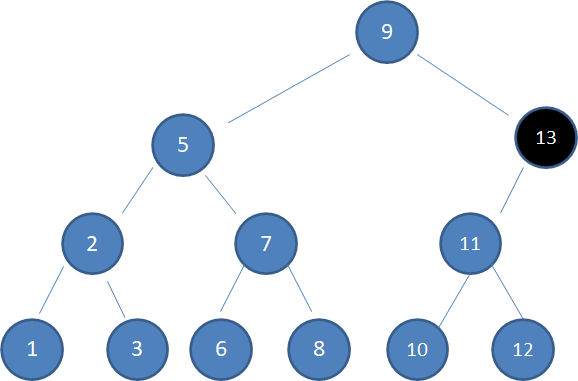
情况2,待删除的结点有一个孩子:
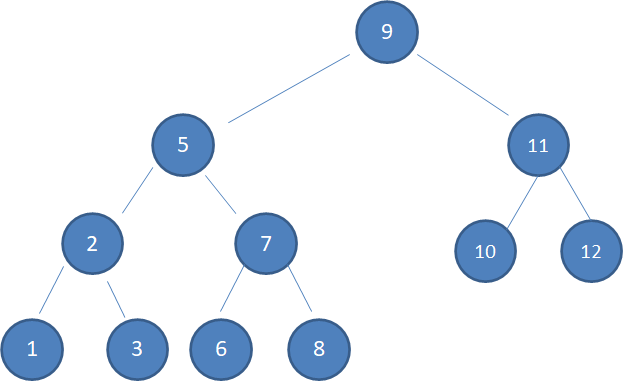
上图中,待删除的结点13只有左孩子,于是我们让左孩子结点11取代被删除的结点,结点11以下的结点关系无需变动:
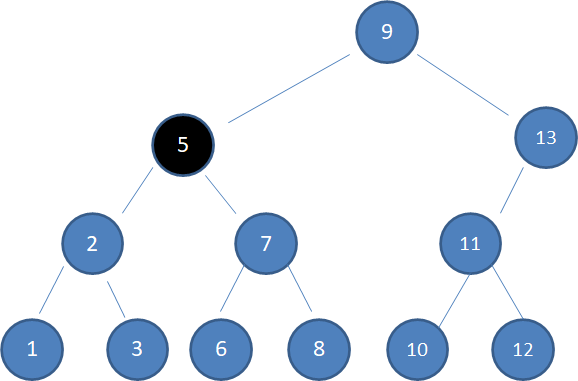
情况3,待删除的结点有两个孩子:
上图中,待删除的结点5有两个孩子,这种情况比较复杂。此时,我们需要选择与待删除结点最接近的结点来取代它。
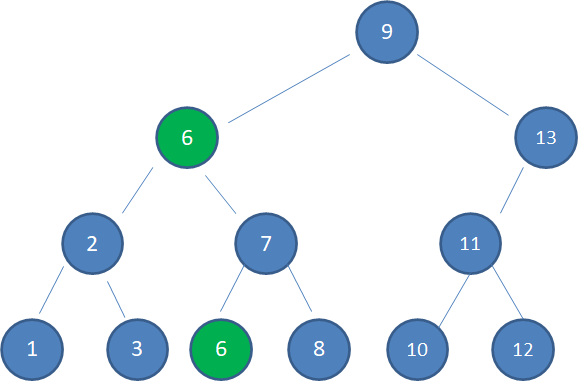
上面的例子中,结点3仅小于结点5,结点6仅大于结点5,两者都是合适的选择。但习惯上我们选择仅大于待删除结点的结点,也就是结点6来取代它。
于是我们复制结点6到原来结点5的位置:
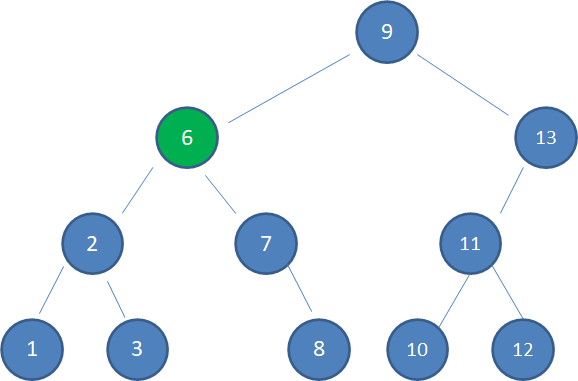
被选中的结点6,仅大于结点5,因此一定没有左孩子。所以我们按照情况1或情况2的方式,删除多余的结点6:



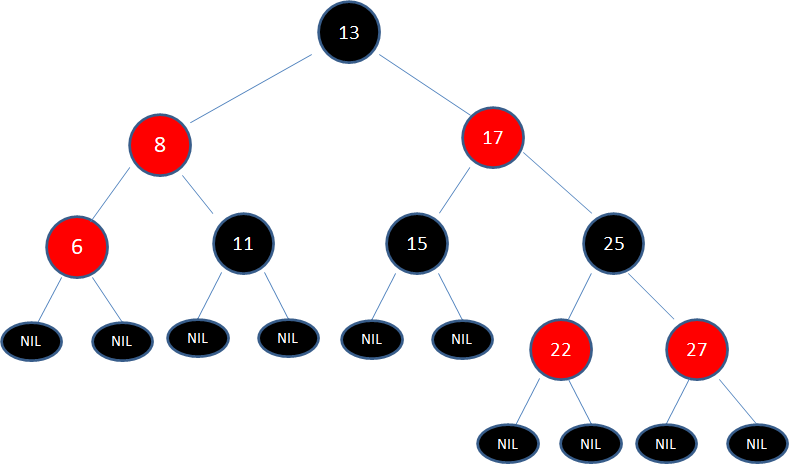
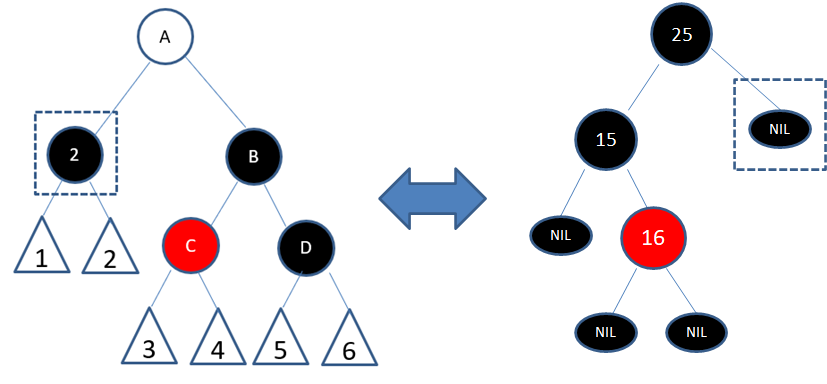
下面我们通过一个例子,来看一看删除红黑树的结点会对规则产生怎样的影响:
显然,这颗新的二叉树打破了两个规则: 规则4. 每个红色结点的两个子结点都是黑色。 规则5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。


第一步:如果待删除结点有两个非空的孩子结点,转化成待删除结点只有一个孩子(或没有孩子)的情况。
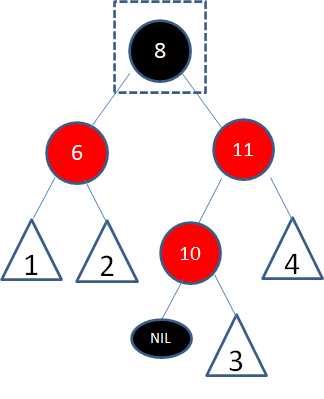
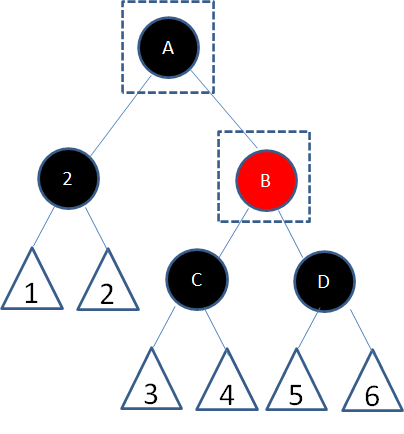
上面例子是一颗红黑树的局部,标数字的三角形代表任意形态的子树,假设结点8是待删除结点。
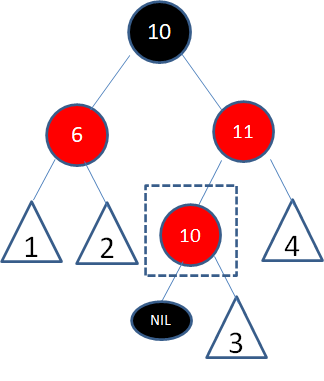
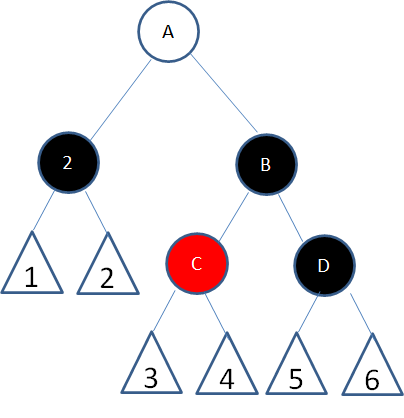
根据上文讲解的二叉查找树删除流程,由于结点8有两个孩子,我们选择仅大于8的结点10复制到8的位置,结点颜色变成待删除结点的颜色:

红色结点10能成为仅大于8的结点,必定没有左孩子结点,所以问题转换成了待删除结点只有一个右孩子(或没有孩子)的情况。接下来我们进入第二步。 第二步:根据待删除结点和其唯一子结点的颜色,分情况处理。 情况1,自身是红色,子结点是黑色:
这种情况最简单,按照二叉查找树的删除操作,删除结点1即可:
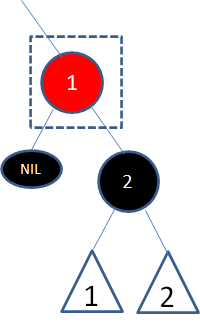
情况2,自身是黑色,子结点是红色:
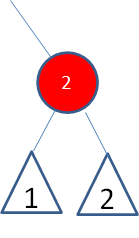
这种情况也很简单,首先按照二叉查找树的删除操作,删除结点1:
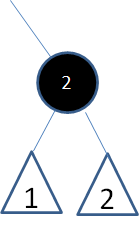
此时,这条路径凭空减少了一个黑色结点,那么我们把结点2变成黑色即可:
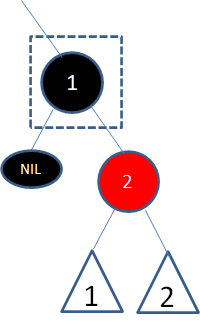
情况3,自身是黑色,子结点也是黑色,或者子结点是空叶子结点:
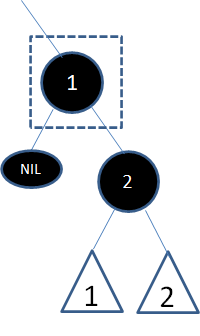
这种情况最复杂,涉及到很多变化。首先我们还是按照二叉查找树的删除操作,删除结点1:
显然,这条路径上减少了一个黑色结点,而且结点2再怎么变色也解决不了。
这时候我们进入第三步,专门解决父子双黑的情况。
第三步:遇到双黑结点,在子结点顶替父结点之后,分成6种子情况处理。
子情况1,结点2是红黑树的根结点:

此时,我们直接把结点2的兄弟结点B改为红色:
这样一来,原本结点2所在的路径少了一个黑色结点,现在结点B所在的路径也少了一个黑色结点,两边“扯平”了。
可是,结点A以下的每一条路径都减少了一个黑色结点,与结点A之外的其他路径又造成了新的不平衡啊?
没关系,我们让结点A扮演原先结点2的角色,进行递归操作,重新判断各种情况。
子情况3,结点2的兄弟结点是红色:
首先以结点2的父结点A为轴,进行左旋:
然后结点A变成红色、结点B变成黑色:
这样的意义是什么呢?结点2所在的路径仍然少一个黑色结点呀?
别急,这样的变化有可能转换成子情况4、5、6中的任意一种,在子情况4、5、6当中会进一步解决。
子情况4,结点2的父结点是红色,兄弟和侄子结点是黑色:
这种情况,我们直接让结点2的父结点A变成黑色,兄弟结点B变成红色:
这样一来,结点2的路径补充了黑色结点,而结点B的路径并没有减少黑色结点,重新符合了红黑树的规则。
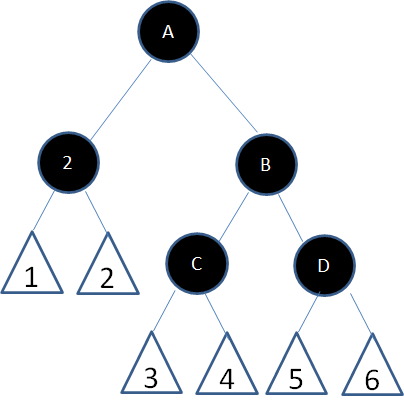
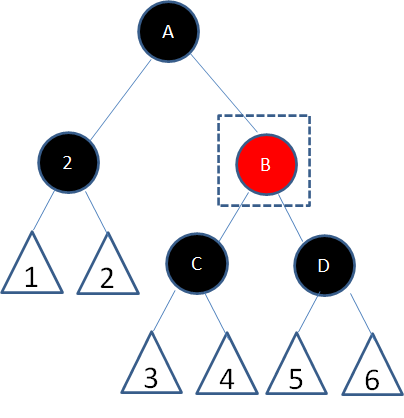
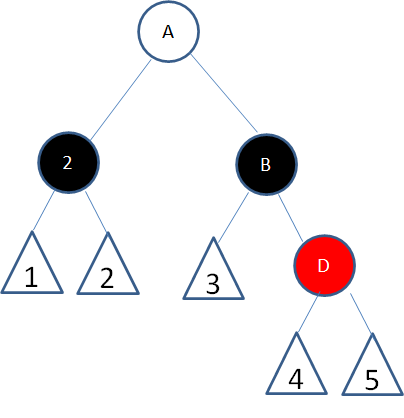
子情况5,结点2的父结点随意,兄弟结点B是黑色右孩子,左侄子结点是红色,右侄子结点是黑色:
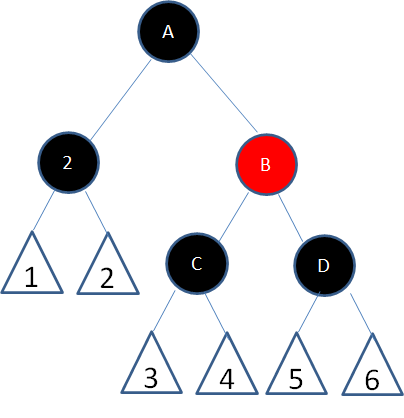
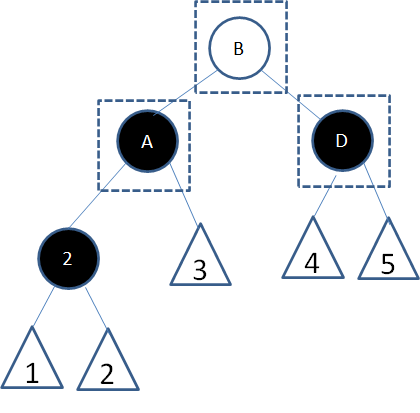
这种情况下,首先以结点2的兄弟结点B为轴进行右旋:
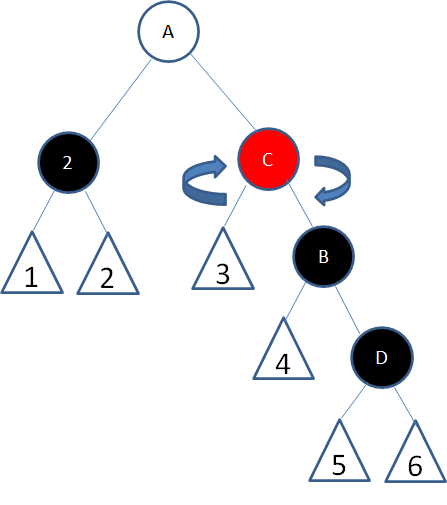
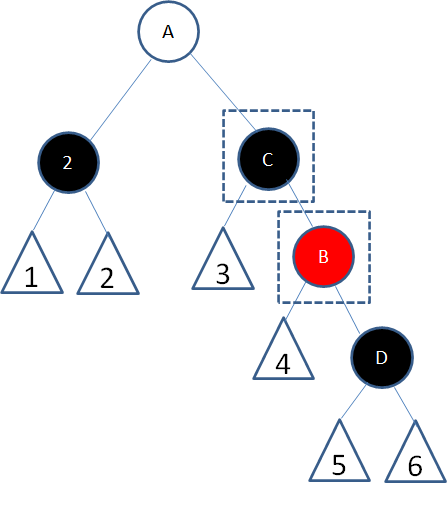
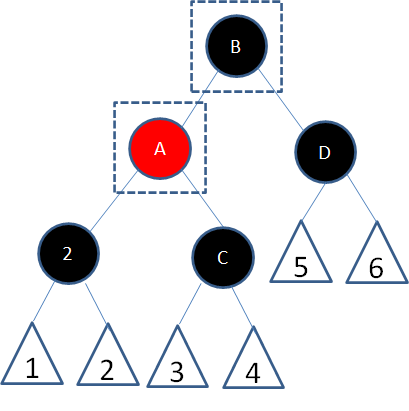
首先以结点2的父结点A为轴左旋:
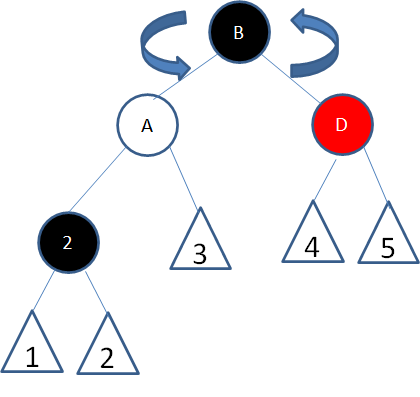
这样是否解决了问题呢?
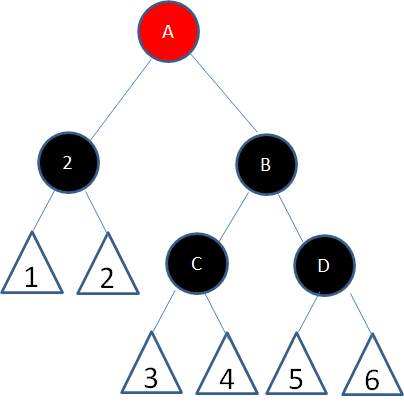
经过结点2的路径由(随意+黑)变成了(随意+黑+黑),补充了一个黑色结点;
经过结点D的路径由(随意+黑+红)变成了(随意+黑),黑色结点并没有减少。
所以,这时候重新符合了红黑树的规则。
以上就是红黑树删除的全过程。


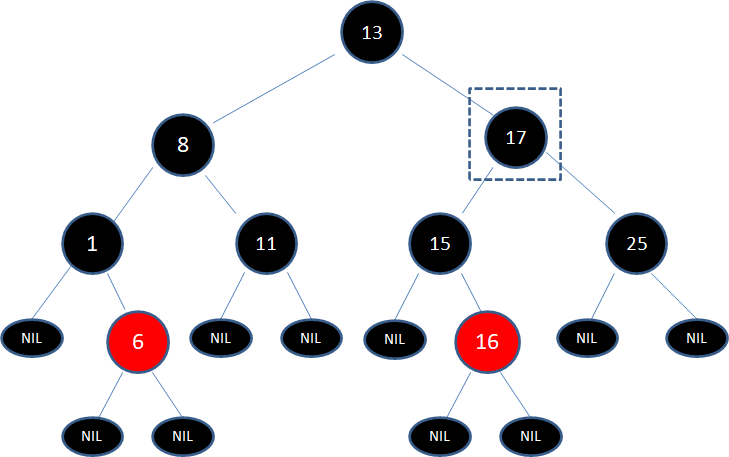
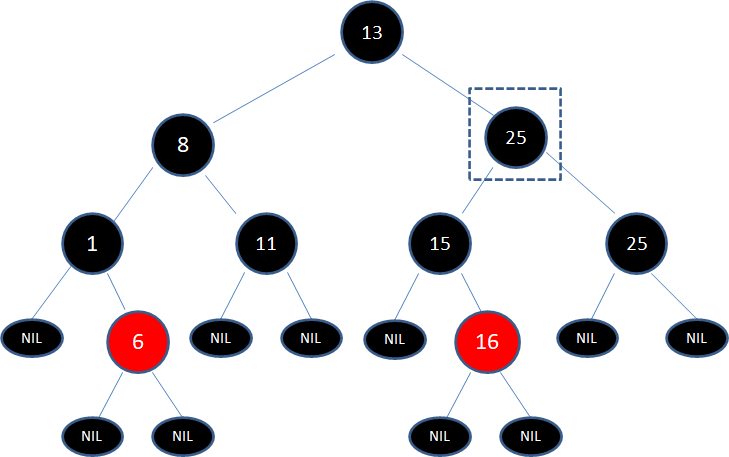
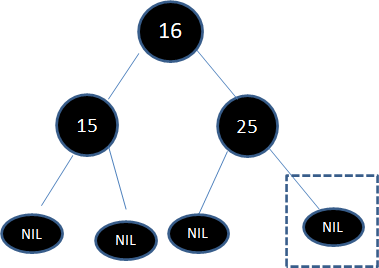
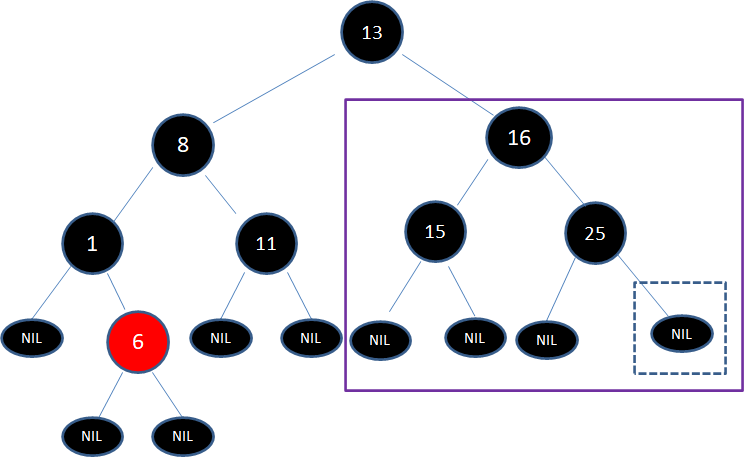
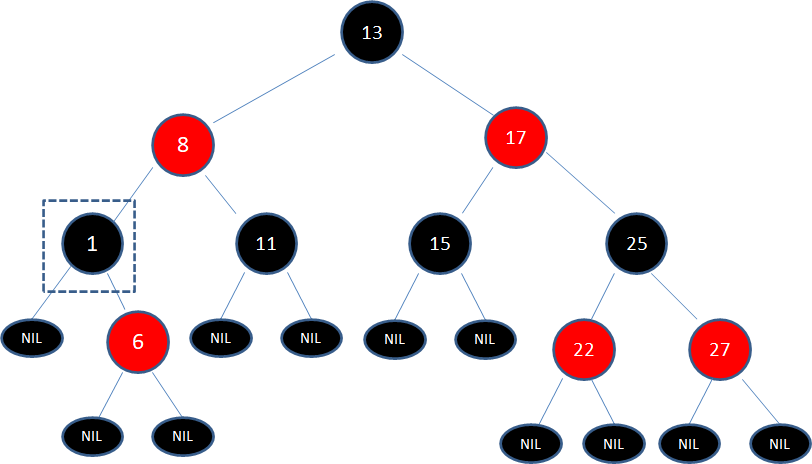
第一步,由于结点17有两个孩子,子树当中仅大于17的结点是25,所以把结点25复制到17位置,保持黑色:
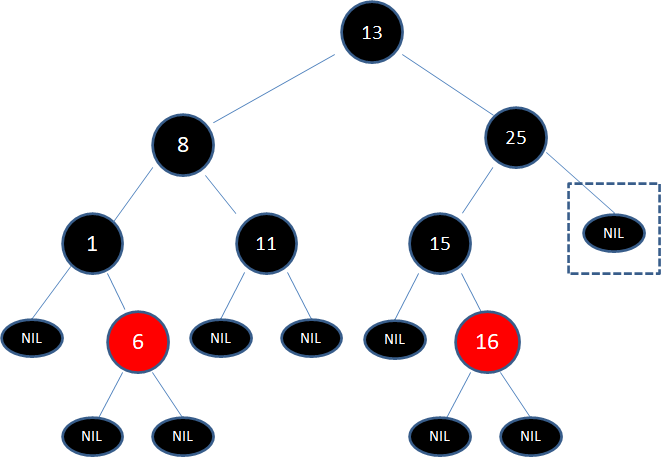
接下来,我们需要删除原本的结点25:
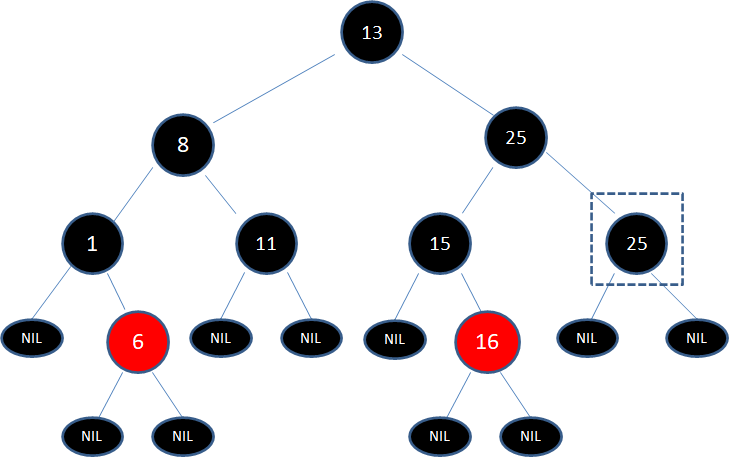
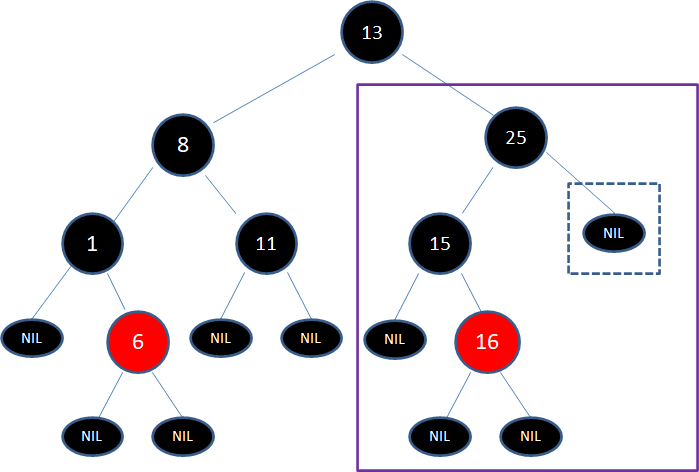
此时,框框中的结点虽然是空叶子结点,但仍然可以用于判断局面,当前局面符合子情况5的镜像:
于是我们通过左旋和变色,把子树转换成情况6的镜像:
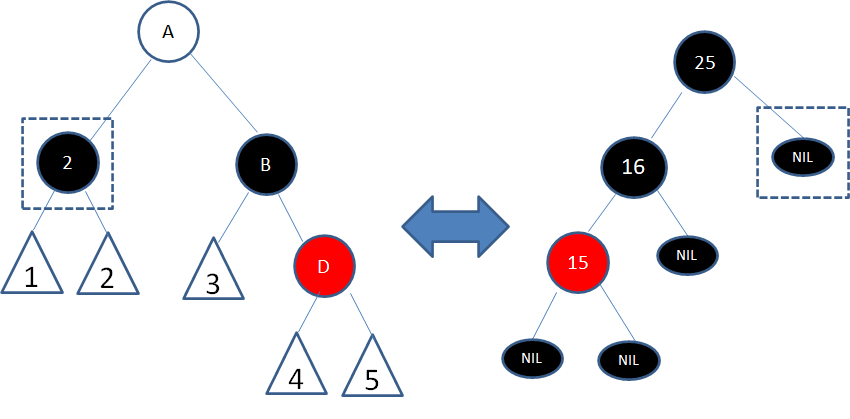
这样一来,整颗二叉树又重新符合了红黑树的规则。