九种查找算法
时间、空间复杂度比较
1.顺序查找 平均时间复杂度:O(n) 空间复杂度:O(1) 查找条件:无序或有序
2.二分查找(折半查找) 平均时间复杂度 :O(log2n) 空间复杂度:O(1) 查找条件:有序
3.插值查找 平均时间复杂度 :O(log2(log2n)) 空间复杂度:O(1) 查找条件:有序
4.斐波那契查找 平均时间复杂度 :O(log2n) 空间复杂度:O(1) 查找条件:有序
5.哈希查找 平均时间复杂度 :O(1) 空间复杂度:O(n) 查找条件:无序或有序
6.二叉查找树(二叉搜索树查找) 平均时间复杂度 :O(log2n)
7.红黑树 平均时间复杂度 :O(log2n)
8.2-3树 平均时间复杂度 :O(log2n - log3n)
9.B树/B+树 平均时间复杂度 :O(log2n)
1 顺序查找
算法思路:
对于任意一个序列,从一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
代码:
#include <stdio.h>
#include <stdlib.h>
#define keyType int
//2020.05.24
typedef struct
{
keyType key;//查找表中每个数据元素的值
}ElemType;
typedef struct
{
ElemType *elem;//存放查找表中数据元素的数组
int length;//记录查找表中数据的总数量
}SSTable;
//创建查询数据
void Create(SSTable **st,int length)
{
(*st)=(SSTable*)malloc(sizeof(SSTable));
(*st)->length=length;
(*st)->elem =(ElemType*)malloc((length+1)*sizeof(ElemType));
printf("输入表中的数据元素:\n");
//根据查找表中数据元素的总长度,在存储时,从数组下标为 1 的空间开始存储数据
for (int i=1; i<=length; i++)
{
scanf("%d",&((*st)->elem[i].key));
}
}
//顺序查找函数,其中key为要查找的元素
int Search_seq(SSTable *str,keyType key)
{
//str->elem[0].key=key;//将关键字作为一个数据元素存放到查找表的第一个位置,起监视哨的作用
int len = str->length;
//从最后一个数据元素依次遍历,一直遍历到数组下标为0
for(int i=1; i<len+1; i++) //创建数据从数组下标为1开始,查询也从1开始
{
if(str->elem[i].key == key)
{
return i;
}
}
//如果 i=0,说明查找失败;查找成功返回要查找元素key的位置i
return 0;
}
int main()
{
SSTable *str;
int num;
printf("请输入创建数据元素的个数:\n");
scanf("%d",&num);
Create(&str, num);
getchar();
printf("请输入要查找的数据:\n");
int key;
scanf("%d",&key);
int location=Search_seq(str, key);
if (location==0) {
printf("查找失败");
}else{
printf("要查找的%d的顺序为:%d",key,location);
}
return 0;
}运行结果:
查找成功!
查找失败
2 二分查找(折半查找)
算法思路:
- 确定查找范围low=0,high=N-1,计算中项mid=(low+high)/2。
- 若mid==x或low>=high,则结束查找;否则,向下继续。
- 若amid<x,说明待查找的元素值只可能在比中项元素大的范围内,则把mid+1的值赋给low,并重新计算mid,转去执行步骤2;若mid>x,说明待查找的元素值只可能在比中项元素小的范围内,则把mid-1的值赋给higt,并重新计算mid,转去执行步骤2。
说明:
- 查找元素必须是有序的,如果是无序的则要先进行排序操作。
- 在做查找的过程中,如果 low 指针和 high 指针的中间位置在计算时位于两个关键字中间,即求得 mid 的位置不是整数,需要统一做取整操作。
折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用。 ——《大话数据结构》
代码:
#include <stdio.h>
#include <stdlib.h>
#define keyType int
typedef struct
{
keyType key;//查找表中每个数据元素的值
}ElemType;
typedef struct
{
ElemType *elem;//存放查找表中数据元素的数组
int length;//记录查找表中数据的总数量
}SSTable;
//创建查询数据
void Create(SSTable **st,int length)
{
(*st)=(SSTable*)malloc(sizeof(SSTable));
(*st)->length=length;
(*st)->elem =(ElemType*)malloc((length+1)*sizeof(ElemType));
printf("输入表中的数据元素:\n");
//根据查找表中数据元素的总长度,在存储时,从数组下标为 1 的空间开始存储数据
for (int i=1; i<=length; i++)
{
scanf("%d",&((*st)->elem[i].key));
}
}
//折半查找函数 key为要查找的元素
int Search_Bin(SSTable *str,keyType key)
{
int low=1;//初始状态 low 指针指向第一个关键字
int high=str->length;//high 指向最后一个关键字
int mid;
while (low<=high)
{
mid=(low+high)/2;//int 本身为整形,所以,mid 每次为取整的整数
if(str->elem[mid].key==key)//如果 mid 指向的同要查找的相等,返回 mid 所指向的位置
{
return mid;
}
else if(str->elem[mid].key>key)//如果mid指向的关键字较大,则更新 high 指针的位置
{
high=mid-1;
}
//反之,则更新 low 指针的位置
else
{
low=mid+1;
}
}
return 0;
}
int main()
{
SSTable *str;
int num;
printf("请输入创建数据元素的个数:\n");
scanf("%d",&num);
Create(&str, num);
getchar();
printf("请输入要查找的数据:\n");
int key;
scanf("%d",&key);
int location=Search_Bin(str, key);
if (location==0) {
printf("没有查找到");
}else{
printf("要查找的%d的顺序为:%d",key,location);
}
return 0;
}运行结果:
查找成功
没有查找到
3 插值查找
插值查找基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。当然,差值查找也属于有序查找
算法思路:
- 确定查找范围low=0,high=N-1,计算中项mid=low+(key-a[low])/(a[high]-a[low])*(high-low)。
- 若mid==x或low>=high,则结束查找;否则,向下继续。
- 若amid<x,说明待查找的元素值只可能在比中项元素大的范围内,则把mid+1的值赋给low,并重新计算mid,转去执行步骤2;若mid>x,说明待查找的元素值只可能在比中项元素小的范围内,则把mid-1的值赋给higt,并重新计算mid,转去执行步骤2。
说明:
- 插值查找是基于折半查找进行了优化的查找方法。
- 当表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能要比折半查找要好得多。
代码:
#include<stdio.h>
int array[10] = { 1, 4, 9, 16, 27, 31, 33, 35, 45, 64 };
int InsertionSearch(int data)
{
int low = 0;
int high = 10 - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(low <= high)
{
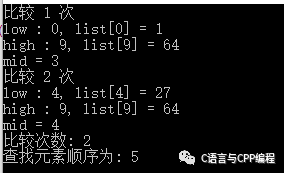
printf("比较 %d 次\n" , comparisons );
printf("low : %d, list[%d] = %d\n", low, low, array[low]);
printf("high : %d, list[%d] = %d\n", high, high, array[high]);
comparisons++;
mid = low + (((double)(high - low) / (array[high] - array[low])) * (data - array[low]));
printf("mid = %d\n",mid);
// 没有找到
if(array[mid] == data)
{
index = mid;
break;
}
else
{
if(array[mid] < data)
{
low = mid + 1;
}
else
{
high = mid - 1;
}
}
}
printf("比较次数: %d\n", --comparisons);
return index;
}
int main()
{
int location = InsertionSearch(27); //测试代,查27,可以找到
if(location != -1)
{
printf("查找元素顺序为: %d\n" ,(location+1));
}
else
{
printf("没有查找到");
}
return 0;
}
运行结果:
运行结果
4 斐波那契查找
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=F(k)-1;开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1).
算法思路:
- 相等,mid位置的元素即为所求
- 大于,low=mid+1,k-=2;
- 小于,high=mid-1,k-=1。
说明:
low=mid+1说明待查找的元素在[mid+1,high]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找。
代码:
#include "stdafx.h"
#include <memory>
#include <iostream>
using namespace std;
const int max_size=20;//斐波那契数组的长度
/*构造一个斐波那契数组*/
void Fibonacci(int * F)
{
F[0]=0;
F[1]=1;
for(int i=2;i<max_size;++i)
F[i]=F[i-1]+F[i-2];
}
/*定义斐波那契查找法*/
int FibonacciSearch(int *a, int n, int key) //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字
{
int low=0;
int high=n-1;
int F[max_size];
Fibonacci(F);//构造一个斐波那契数组F
int k=0;
while(n>F[k]-1)//计算n位于斐波那契数列的位置
++k;
int * temp;//将数组a扩展到F[k]-1的长度
temp=new int [F[k]-1];
memcpy(temp,a,n*sizeof(int));
for(int i=n;i<F[k]-1;++i)
temp[i]=a[n-1];
while(low<=high)
{
int mid=low+F[k-1]-1;
if(key<temp[mid])
{
high=mid-1;
k-=1;
}
else if(key>temp[mid])
{
low=mid+1;
k-=2;
}
else
{
if(mid<n)
return mid; //若相等则说明mid即为查找到的位置
else
return n-1; //若mid>=n则说明是扩展的数值,返回n-1
}
}
delete [] temp;
return 0;
}
int main()
{
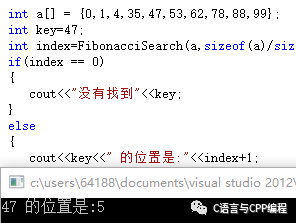
int a[] = {0,1,4,35,47,53,62,78,88,99};
int key=47;
int index=FibonacciSearch(a,sizeof(a)/sizeof(int),key);
if(index == 0)
{
cout<<"没有找到"<<key;
}
else
{
cout<<key<<" 的位置是:"<<index;
}
return 0;
}运行结果:
47的位置为5
5 哈希查找
哈希表:
我们使用一个下标范围比较大的数组来存储元素。可以设计一个函数(哈希函数, 也叫做散列函数),使得每个元素的关键字都与一个函数值(即数组下标)相对应,于是用这个数组单元来存储这个元素;也可以简单的理解为,按照关键字为每一个元素"分类",然后将这个元素存储在相应"类"所对应的地方。但是,不能够保证每个元素的关键字与函数值是一一对应的,因此极有可能出现对于不同的元素,却计算出了相同的函数值,这样就产生了"冲突",换句话说,就是把不同的元素分在了相同的"类"之中。后面我们将看到一种解决"冲突"的简便做法。
"直接定址"与"解决冲突"是哈希表的两大特点。
哈希函数:
规则:通过某种转换关系,使关键字适度的分散到指定大小的的顺序结构中,越分散,则以后查找的时间复杂度越小,空间复杂度越高。
算法思路:
如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键。
- 用给定的哈希函数构造哈希表;
- 根据选择的冲突处理方法(常见方法:拉链法和线性探测法)解决地址冲突;
- 在哈希表的基础上执行哈希查找;
代码:
#include<stdio.h>
#include<stdlib.h>
#define SUCCESS 1
#define UNSUCCESS 0
#define OVERFLOW -1
#define OK 1
#define ERROR -1
#define MAXNUM 9999 // 用于初始化哈希表的记录 key
typedef int Status;
typedef int KeyType;
// 哈希表中的记录类型
typedef struct
{
KeyType key;
}RcdType;
// 哈希表类型
typedef struct
{
RcdType *rcd;
int size;
int count;
int *tag;
}HashTable;
// 哈希表每次重建增长后的大小
int hashsize[] = { 11, 31, 61, 127, 251, 503 };
int index = 0;
// 初始哈希表
Status InitHashTable(HashTable &H, int size)
{
int i;
H.rcd = (RcdType *)malloc(sizeof(RcdType)*size);
H.tag = (int *)malloc(sizeof(int)*size);
if (NULL == H.rcd || NULL == H.tag) return OVERFLOW;
KeyType maxNum = MAXNUM;
for (i = 0; i < size; i++)
{
H.tag[i] = 0;
H.rcd[i].key = maxNum;
}
H.size = size;
H.count = 0;
return OK;
}
// 哈希函数:除留余数法
int Hash(KeyType key, int m)
{
return (3 * key) % m;
}
// 处理哈希冲突:线性探测
void collision(int &p, int m)
{
p = (p + 1) % m;
}
// 在哈希表中查询
Status SearchHash(HashTable H, KeyType key, int &p, int &c)
{
p = Hash(key, H.size);
int h = p;
c = 0;
while ((1 == H.tag[p] && H.rcd[p].key != key) || -1 == H.tag[p])
{
collision(p, H.size); c++;
}
if (1 == H.tag[p] && key == H.rcd[p].key) return SUCCESS;
else return UNSUCCESS;
}
//打印哈希表
void printHash(HashTable H)
{
int i;
printf("key : ");
for (i = 0; i < H.size; i++)
printf("%3d ", H.rcd[i].key);
printf("\n");
printf("tag : ");
for (i = 0; i < H.size; i++)
printf("%3d ", H.tag[i]);
printf("\n\n");
}
// 函数声明:插入哈希表
Status InsertHash(HashTable &H, KeyType key);
// 重建哈希表
Status recreateHash(HashTable &H)
{
RcdType *orcd;
int *otag, osize, i;
orcd = H.rcd;
otag = H.tag;
osize = H.size;
InitHashTable(H, hashsize[index++]);
//把所有元素,按照新哈希函数放到新表中
for (i = 0; i < osize; i++)
{
if (1 == otag[i])
{
InsertHash(H, orcd[i].key);
}
}
return OK;
}
// 插入哈希表
Status InsertHash(HashTable &H, KeyType key)
{
int p, c;
if (UNSUCCESS == SearchHash(H, key, p, c))
{ //没有相同key
if (c*1.0 / H.size < 0.5)
{ //冲突次数未达到上线
//插入代码
H.rcd[p].key = key;
H.tag[p] = 1;
H.count++;
return SUCCESS;
}
else recreateHash(H); //重构哈希表
}
return UNSUCCESS;
}
// 删除哈希表
Status DeleteHash(HashTable &H, KeyType key)
{
int p, c;
if (SUCCESS == SearchHash(H, key, p, c))
{
//删除代码
H.tag[p] = -1;
H.count--;
return SUCCESS;
}
else return UNSUCCESS;
}
int main()
{
printf("-----哈希表-----\n");
HashTable H;
int i;
int size = 11;
KeyType array[8] = { 22, 41, 53, 46, 30, 13, 12, 67 };
KeyType key;
//初始化哈希表
printf("初始化哈希表\n");
if (SUCCESS == InitHashTable(H, hashsize[index++])) printf("初始化成功\n");
//插入哈希表
printf("插入哈希表\n");
for (i = 0; i <= 7; i++)
{
key = array[i];
InsertHash(H, key);
printHash(H);
}
//删除哈希表
printf("删除哈希表中key为12的元素\n");
int p, c;
if (SUCCESS == DeleteHash(H, 12))
{
printf("删除成功,此时哈希表为:\n");
printHash(H);
}
//查询哈希表
printf("查询哈希表中key为67的元素\n");
if (SUCCESS == SearchHash(H, 67, p, c)) printf("查询成功\n");
//再次插入,测试哈希表的重建
printf("再次插入,测试哈希表的重建:\n");
KeyType array1[8] = { 27, 47, 57, 47, 37, 17, 93, 67 };
for (i = 0; i <= 7; i++)
{
key = array1[i];
InsertHash(H, key);
printHash(H);
}
getchar();
return 0;
}6 二叉树查找
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
算法思路:
- 若b是空树,则搜索失败:
- 若x等于b的根节点的数据域之值,则查找成功:
- 若x小于b的根节点的数据域之值,则搜索左子树:
- 查找右子树。
代码:
递归和非递归
//非递归查找算法
BSTNode *BST_Search(BiTree T,ElemType key,BSTNode *&p)
{
//查找函数返回指向关键字值为key的结点指针,不存在则返回NULL
p=NULL;
while(T!=NULL&&key!=T->data)
{
p=T; //指向被查找结点的双亲
if(key<T->data)
T=T->lchild; //查找左子树
else
T=T->rchild; //查找右子树
}
return T;
}
//递归算法
Status Search_BST(BiTree T, int key, BiTree f, BiTree *p)
{
//查找BST中是否存在key,f指向T双亲,其初始值为NULL
//若查找成功,指针p指向数据元素结点,返回true;
//若失败,p指向查找路径上访问的最后一个结点并返回false
if(!T)
{
*p=f;
return false;
}
else if(key==T->data)
{ //查找成功
*p=T;
return true;
}
else if(key<T->data)
return Search_BST(T->lchild,key,T,p); //递归查找左子树
else
return Search_BST(T->rchild,key,T,p); //递归查找右子树
}7 2-3树
2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node),他保存1个key和左右两个自己点。对应3节点(3-node),保存两个Key,2-3查找树的定义如下:
- 要么为空,要么:
- 对于2节点,该节点保存一个key及对应value,以及两个指向左右节点的节点,左节点也是一个2-3节点,所有的值都比key要小,右节点也是一个2-3节点,所有的值比key要大。
- 对于3节点,该节点保存两个key及对应value,以及三个指向左中右的节点。左节点也是一个2-3节点,所有的值均比两个key中的最小的key还要小;中间节点也是一个2-3节点,中间节点的key值在两个跟节点key值之间;右节点也是一个2-3节点,节点的所有key值比两个key中的最大的key还要大。
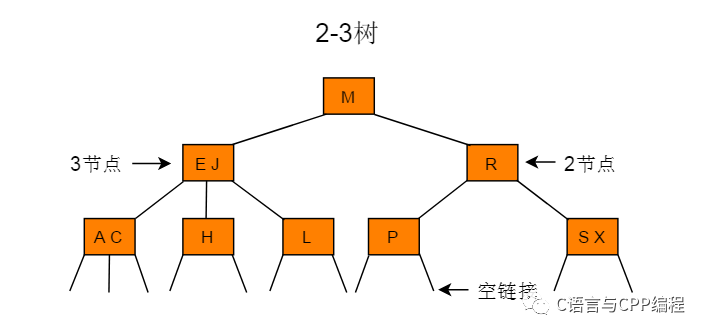
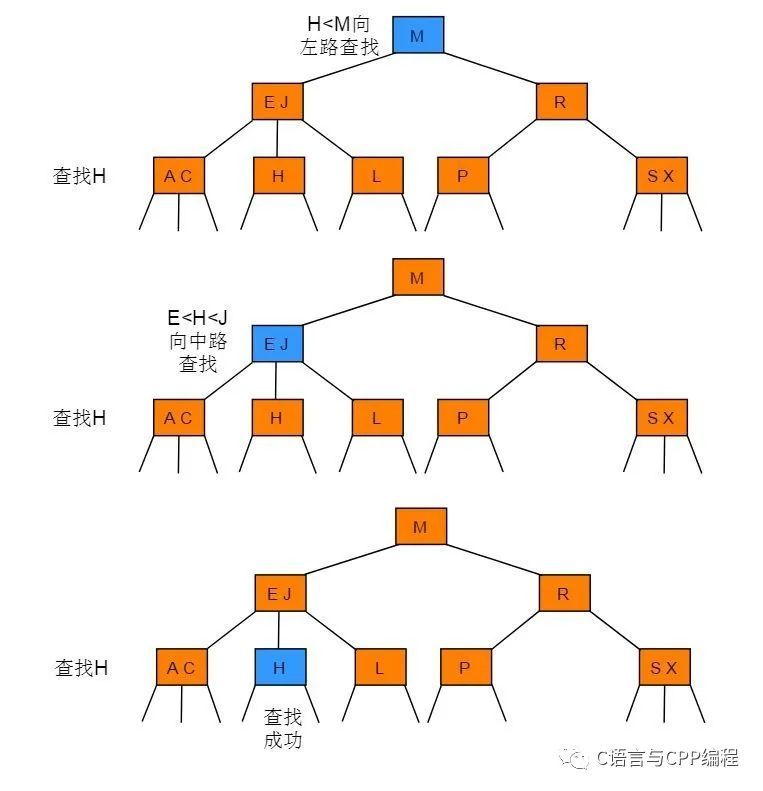
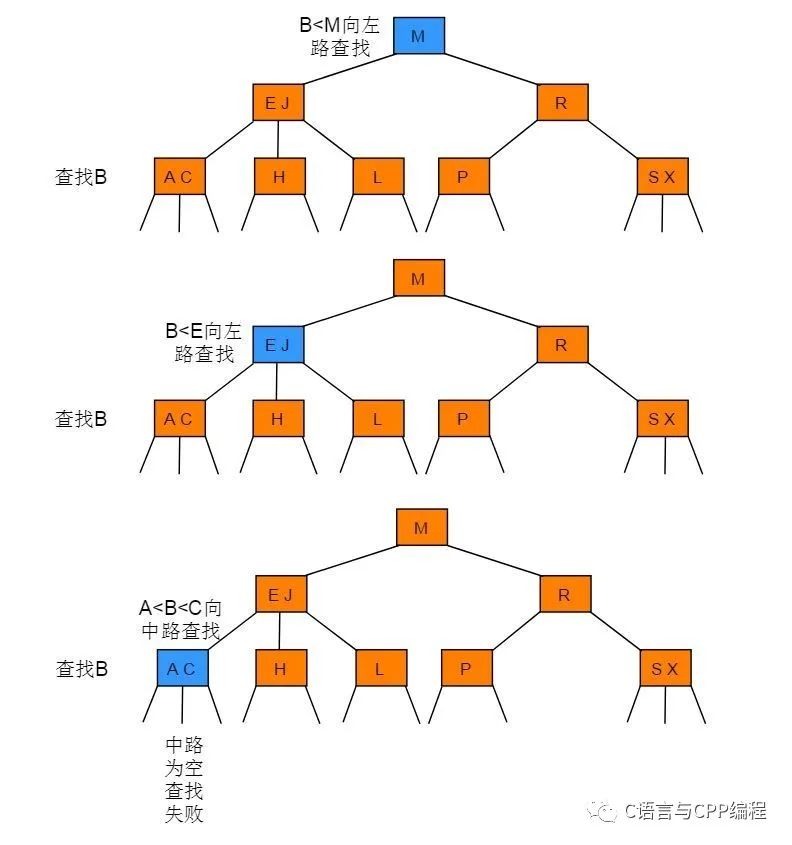
要判断一个键是否在树中,我们先将它和根结点中的键比较。如果它和其中的任何一个相等,查找命中。否则我们就根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归地继续查找。如果这是个空链接,查找未命中。
2-3 树中查找键为H的节点
2-3 树中查找键为B的节点
代码:
two_three *search23(two_three *t, element x)
{
while(t)
{
if (x < t->data_l)
{
t = t->left_child;
}
else if (x > t->data_l && x < t->data_r)
{
t = t->middle_child;
}
else if (x > t->data_r)
{
t = t->right_child;
}
else
{
return t;
}
}
return NULL;
}8 红黑树
2-3查找树能保证在插入元素之后能保持树的平衡状态,最坏情况下即所有的子节点都是2-node,树的高度为lgn,从而保证了最坏情况下的时间复杂度。但是2-3树实现起来比较复杂,于是就有了一种简单实现2-3树的数据结构,即红黑树(Red-Black Tree)。
理解红黑树一句话就够了:红黑树就是用红链接表示3-结点的2-3树。
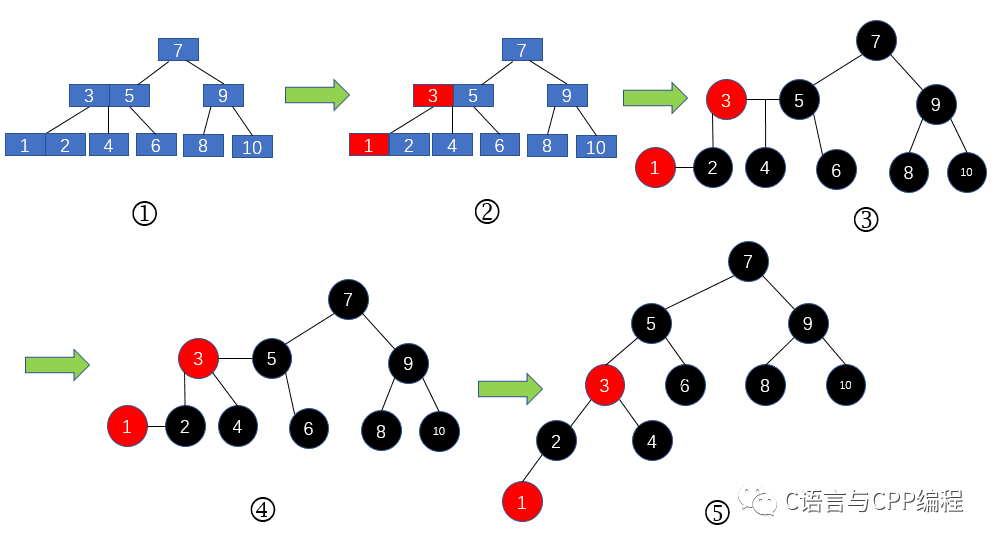
现在我们对2-3树进行改造,改造成一个二叉树。怎么改造呢?对于2节点,保持不变;对于3节点,我们首先将3节点中左侧的元素标记为红色,然后我们将其改造成图3的形式;
再将3节点的位于中间的子节点的父节点设置为父节点中那个红色的节点,如图4的所示;最后我们将图4的形式改为二叉树的样子,如图5所示。图5是不是很熟悉,没错,这就是我们常常提到的大名鼎鼎的红黑树了。如下图所示。
2-3树转红黑树
为什么使用红黑树:
- 红黑树是一种平衡树,他复杂的定义和规则都是为了保证树的平衡性。如果树不保证他的平衡性就是下图:很显然这就变成一个链表了。
- 保证平衡性的最大的目的就是降低树的高度,因为树的查找性能取决于树的高度。所以树的高度越低搜索的效率越高!
- 这也是为什么存在二叉树、搜索二叉树等,各类树的目的。
红黑树性质:
- 每个节点要么是黑色,要么是红色。
- 根节点是黑色。
- 每个叶子节点(NIL)是黑色。
- 每个红色结点的两个子结点一定都是黑色。
- 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
算法思路:
红黑树的思想就是对2-3查找树进行编码,尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型,红色链接,他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的,使用红色链接的两个2-nodes来表示一个3-nodes节点,并且向左倾斜,即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改,和普通的二叉查找树相同。
代码:
#define BLACK 1
#define RED 0
#include <iostream>
using namespace std;
class bst
{
private:
struct Node
{
int value;
bool color;
Node *leftTree, *rightTree, *parent;
Node() : value(0), color(RED), leftTree(NULL), rightTree(NULL), parent(NULL) { }
Node* grandparent()
{
if (parent == NULL)
{
return NULL;
}
return parent->parent;
}
Node* uncle()
{
if (grandparent() == NULL)
{
return NULL;
}
if (parent == grandparent()->rightTree)
return grandparent()->leftTree;
else
return grandparent()->rightTree;
}
Node* sibling()
{
if (parent->leftTree == this)
return parent->rightTree;
else
return parent->leftTree;
}
};
void rotate_right(Node *p)
{
Node *gp = p->grandparent();
Node *fa = p->parent;
Node *y = p->rightTree;
fa->leftTree = y;
if (y != NIL)
y->parent = fa;
p->rightTree = fa;
fa->parent = p;
if (root == fa)
root = p;
p->parent = gp;
if (gp != NULL)
{
if (gp->leftTree == fa)
gp->leftTree = p;
else
gp->rightTree = p;
}
}
void rotate_left(Node *p)
{
if (p->parent == NULL)
{
root = p;
return;
}
Node *gp = p->grandparent();
Node *fa = p->parent;
Node *y = p->leftTree;
fa->rightTree = y;
if (y != NIL)
y->parent = fa;
p->leftTree = fa;
fa->parent = p;
if (root == fa)
root = p;
p->parent = gp;
if (gp != NULL)
{
if (gp->leftTree == fa)
gp->leftTree = p;
else
gp->rightTree = p;
}
}
void inorder(Node *p)
{
if (p == NIL)
return;
if (p->leftTree)
inorder(p->leftTree);
cout << p->value << " ";
if (p->rightTree)
inorder(p->rightTree);
}
string outputColor(bool color)
{
return color ? "BLACK" : "RED";
}
Node* getSmallestChild(Node *p)
{
if (p->leftTree == NIL)
return p;
return getSmallestChild(p->leftTree);
}
bool delete_child(Node *p, int data)
{
if (p->value > data)
{
if (p->leftTree == NIL)
{
return false;
}
return delete_child(p->leftTree, data);
}
else if (p->value < data)
{
if (p->rightTree == NIL)
{
return false;
}
return delete_child(p->rightTree, data);
}
else if (p->value == data)
{
if (p->rightTree == NIL)
{
delete_one_child(p);
return true;
}
Node *smallest = getSmallestChild(p->rightTree);
swap(p->value, smallest->value);
delete_one_child(smallest);
return true;
}
else
{
return false;
}
}
void delete_one_child(Node *p)
{
Node *child = p->leftTree == NIL ? p->rightTree : p->leftTree;
if (p->parent == NULL && p->leftTree == NIL && p->rightTree == NIL)
{
p = NULL;
root = p;
return;
}
if (p->parent == NULL)
{
delete p;
child->parent = NULL;
root = child;
root->color = BLACK;
return;
}
if (p->parent->leftTree == p)
{
p->parent->leftTree = child;
}
else
{
p->parent->rightTree = child;
}
child->parent = p->parent;
if (p->color == BLACK)
{
if (child->color == RED)
{
child->color = BLACK;
}
else
delete_case(child);
}
delete p;
}
void delete_case(Node *p)
{
if (p->parent == NULL)
{
p->color = BLACK;
return;
}
if (p->sibling()->color == RED)
{
p->parent->color = RED;
p->sibling()->color = BLACK;
if (p == p->parent->leftTree)
rotate_left(p->sibling());
else
rotate_right(p->sibling());
}
if (p->parent->color == BLACK && p->sibling()->color == BLACK
&& p->sibling()->leftTree->color == BLACK && p->sibling()->rightTree->color == BLACK)
{
p->sibling()->color = RED;
delete_case(p->parent);
}
else if (p->parent->color == RED && p->sibling()->color == BLACK
&& p->sibling()->leftTree->color == BLACK && p->sibling()->rightTree->color == BLACK)
{
p->sibling()->color = RED;
p->parent->color = BLACK;
}
else
{
if (p->sibling()->color == BLACK)
{
if (p == p->parent->leftTree && p->sibling()->leftTree->color == RED
&& p->sibling()->rightTree->color == BLACK)
{
p->sibling()->color = RED;
p->sibling()->leftTree->color = BLACK;
rotate_right(p->sibling()->leftTree);
}
else if (p == p->parent->rightTree && p->sibling()->leftTree->color == BLACK
&& p->sibling()->rightTree->color == RED)
{
p->sibling()->color = RED;
p->sibling()->rightTree->color = BLACK;
rotate_left(p->sibling()->rightTree);
}
}
p->sibling()->color = p->parent->color;
p->parent->color = BLACK;
if (p == p->parent->leftTree)
{
p->sibling()->rightTree->color = BLACK;
rotate_left(p->sibling());
}
else
{
p->sibling()->leftTree->color = BLACK;
rotate_right(p->sibling());
}
}
}
void insert(Node *p, int data)
{
if (p->value >= data)
{
if (p->leftTree != NIL)
insert(p->leftTree, data);
else
{
Node *tmp = new Node();
tmp->value = data;
tmp->leftTree = tmp->rightTree = NIL;
tmp->parent = p;
p->leftTree = tmp;
insert_case(tmp);
}
}
else
{
if (p->rightTree != NIL)
insert(p->rightTree, data);
else
{
Node *tmp = new Node();
tmp->value = data;
tmp->leftTree = tmp->rightTree = NIL;
tmp->parent = p;
p->rightTree = tmp;
insert_case(tmp);
}
}
}
void insert_case(Node *p)
{
if (p->parent == NULL)
{
root = p;
p->color = BLACK;
return;
}
if (p->parent->color == RED)
{
if (p->uncle()->color == RED)
{
p->parent->color = p->uncle()->color = BLACK;
p->grandparent()->color = RED;
insert_case(p->grandparent());
}
else
{
if (p->parent->rightTree == p && p->grandparent()->leftTree == p->parent)
{
rotate_left(p);
rotate_right(p);
p->color = BLACK;
p->leftTree->color = p->rightTree->color = RED;
}
else if (p->parent->leftTree == p && p->grandparent()->rightTree == p->parent)
{
rotate_right(p);
rotate_left(p);
p->color = BLACK;
p->leftTree->color = p->rightTree->color = RED;
}
else if (p->parent->leftTree == p && p->grandparent()->leftTree == p->parent)
{
p->parent->color = BLACK;
p->grandparent()->color = RED;
rotate_right(p->parent);
}
else if (p->parent->rightTree == p && p->grandparent()->rightTree == p->parent)
{
p->parent->color = BLACK;
p->grandparent()->color = RED;
rotate_left(p->parent);
}
}
}
}
void DeleteTree(Node *p)
{
if (!p || p == NIL)
{
return;
}
DeleteTree(p->leftTree);
DeleteTree(p->rightTree);
delete p;
}
public:
bst()
{
NIL = new Node();
NIL->color = BLACK;
root = NULL;
}
~bst()
{
if (root)
DeleteTree(root);
delete NIL;
}
void inorder()
{
if (root == NULL)
return;
inorder(root);
cout << endl;
}
void insert(int x)
{
if (root == NULL)
{
root = new Node();
root->color = BLACK;
root->leftTree = root->rightTree = NIL;
root->value = x;
}
else
{
insert(root, x);
}
}
bool delete_value(int data)
{
return delete_child(root, data);
}
private:
Node *root, *NIL;
};
int main()
{
cout << "---【红黑树】---" << endl;
// 创建红黑树
bst tree;
// 插入元素
tree.insert(2);
tree.insert(9);
tree.insert(-10);
tree.insert(0);
tree.insert(33);
tree.insert(-19);
// 顺序打印红黑树
cout << "插入元素后的红黑树:" << endl;
tree.inorder();
// 删除元素
tree.delete_value(2);
// 顺序打印红黑树
cout << "删除元素 2 后的红黑树:" << endl;
tree.inorder();
// 析构
tree.~bst();
getchar();
return 0;
}9 B树/B+树
在计算机科学中,B树(B-tree)是一种树状数据结构,它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树,概括来说是一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同,B-树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程,从而加快存取速度。普遍运用在数据库和文件系统。 ——维基百科
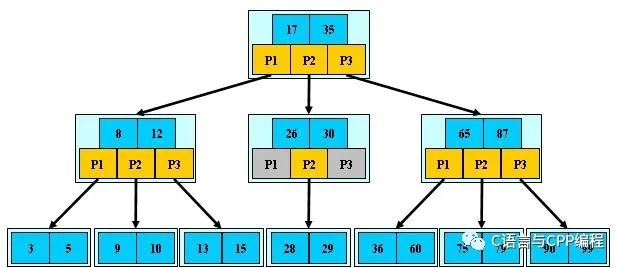
B 树可以看作是对2-3查找树的一种扩展,即他允许每个节点有M-1个子节点。
- 定义任意非叶子结点最多只有M个儿子;且M>2;
- 根结点的儿子数为[2, M];
- 除根结点以外的非叶子结点的儿子数为[M/2, M];
- 每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
- 非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
- 非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的 子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
- 所有叶子结点位于同一层;
如:(M=3)
算法思路:
从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
- 自动层次控制;
代码:
BTNode* BTree_recursive_search(const BTree tree, KeyType key, int* pos)
{
int i = 0;
while (i < tree->keynum && key > tree->key[i])
{
++i;
}
// 查找关键字
if (i < tree->keynum && tree->key[i] == key)
{
*pos = i;
return tree;
}
// tree 为叶子节点,找不到 key,查找失败返回
if (tree->isLeaf)
{
return NULL;
}
// 节点内查找失败,但 tree->key[i - 1]< key < tree->key[i],
// 下一个查找的结点应为 child[i]
// 从磁盘读取第 i 个孩子的数据
disk_read(&tree->child[i]);
// 递归地继续查找于树 tree->child[i]
return BTree_recursive_search(tree->child[i], key, pos);
}B+树:
B+树是B树的变体,也是一种多路搜索树:
其定义基本与B-树同,除了:
- 非叶子结点的子树指针与关键字个数相同;
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树, B树是开区间
- 为所有叶子结点增加一个链指针;
- 所有关键字都在叶子结点出现;
如:(M=3)
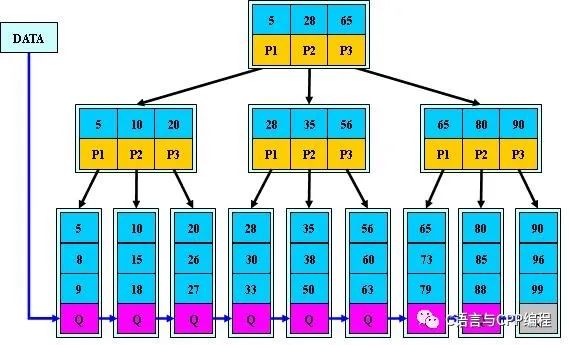
B+的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在 非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
- 不可能在非叶子结点命中;
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
- 更适合文件索引系统;
参考资料
- https://www.sohu.com/a/296278527_478315
- https://www.cnblogs.com/exzlc/p/12203744.html
- 部分配图来源于网络