极客算法训练笔记(三)，链表详细图解，别再逃避了朋友

555次阅读 | 发布于4年以前

缓存引爆链表
链表
单链表
双向链表
循环链表
双向循环链表
LinkedHashMap实现LRU缓存，源码解析（JDK1.8）
算法爬楼梯
算法反转链表
算法链表环检测

缓存引爆链表

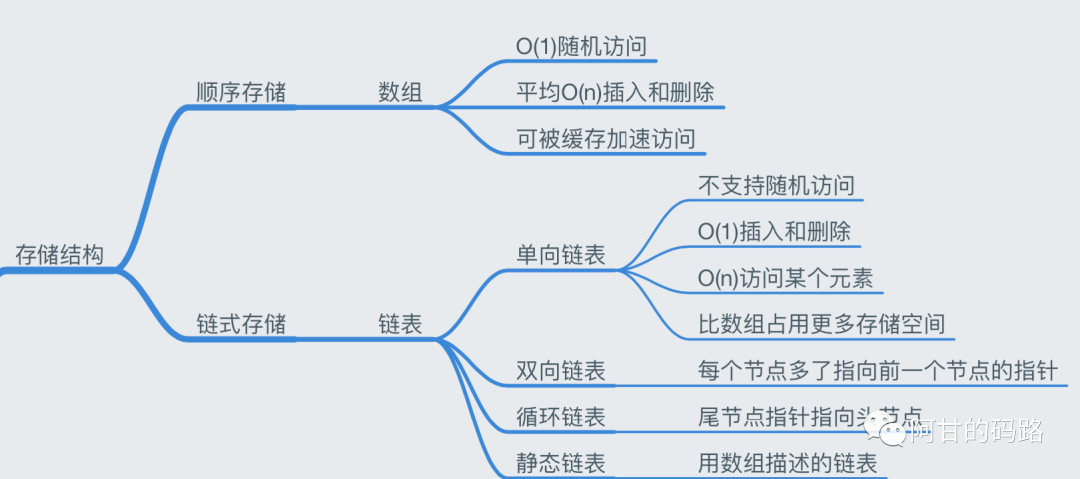
存储结构

上一篇说的是数组，然后现在来说说链表。链表有个经典应用，就是实现LRU缓存淘汰算法，缓存的作用大家肯定都知道，常见的Redis缓存，CPU缓存，数据库缓存，浏览器缓存，预热缓存等等缓存技术。缓存大小有限，当缓存满了，需要淘汰策略来决定哪些数据出局，常见缓存算法有三种，这里以缓存中数据命中率来评判缓存算法的优劣来看三种淘汰算法：

1.FIFO（First in, First out），先进先出策略，不管你是谁，排好队一个一个来，这种做法简单粗暴公平，但是显然是没有考虑缓存数据的使用频率问题了，所以这种算法使用不多； 2.LFU（Least Frequently Used），最近最不频繁使用策略，即最近最少使用到的数据出局，是从时间和数据使用频率来决定的，

实现：LFU的每个数据块都有一个引用计数，所有数据块按照引用计数排序，具有相同引用计数的数据块则按照时间排序；
缺点：需要记录所有数据的访问记录，内存消耗较高；需要基于引用计数排序，时间消耗较高；

3.LRU（Least Recently Used），最近最久未使用策略，主要是从时间来进行淘汰，如果一个数据在最近一段时间没有被访问到，那么可以认为在将来它被访问的可能性也很小，把这些数据淘汰掉。

实现：不就是需要根据时间来淘汰嘛，最容易想到的就是数组+时间戳，但是这样实现不用想也知道效率贼低。因此java 中的 「LinkedHashMap」 源码就是使用这种缓存算法，底层用 双向链表（LinkedList）+哈希表（HashMap）实现（链表用来表示位置，哈希表用来存储和查找），下面我会把这部分源码进行剖析；
应用：现在使用最广泛的分布式缓存系统如Redis，Memchached，容器如LinkedHashMap 就使用了这种缓存算法，

4.LRU 和LFU 区别：

LRU:活在当下。比如在公司中，一个新员工做出新业绩，马上会得到重用。

LFU:以史为镜。还是比如在公司中，新员工必须做出比老员工累计更多更好的业绩才可以受到老板重视，这样的方式比较尊重“前辈”。

因此，我们可以就知道链表的伟大贡献了，看到了作用我才去学你懂你，这是我一贯的作风，要不然我学你做什么。

链表

上一节说数组的时候，我一直强调要一段连续的空间，链表就不需要，他是通过“指针”将一组零散的内存块串联起来使用，不需要连续只要有空间就够了。所以链表结点除了数据之外，比数组多存储了个“指针”，数组是靠数组下标偏移量（计算出地址偏移位）找数据，链表是靠指针（直接存储地址）找数据。

在操作链表的时候，要格外注意二点：

边界问题，例如插入有头插尾插中间插入，要注意额外的操作；
代码顺序，防止丢失指针

单链表

链表

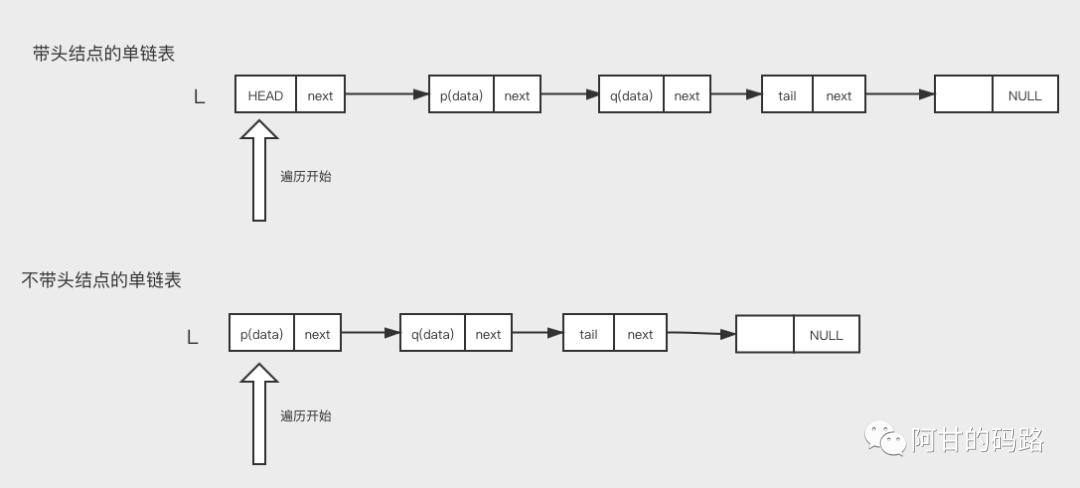
首先理解两个概念：

头指针：通常使用“头指针”来标识一个链表，如单链表L，头指针为NULL的时表示一个空链表。
头结点：在单链表的第一个结点之前附加一个结点，称为头结点。头结点的Data域可以不设任何信息，也可以记录表长等相关信息。

不管你有没有头结点，头指针始终是有的，代表了链表的基地址，有基地址才能遍历。头指针始终指向第一个结点，有头结点就指向头结点。

「带头结点好处」

方便第一个位置的插入和删除
统一空表和非空表的处理

有头结点可以简化很多边界问题的考虑，将边界问题转化为正常的结点处理。

最后一个是尾结点，尾结点不指向下一个结点，而是指向空地址NULL，代表这个链表结束了。

中间插入

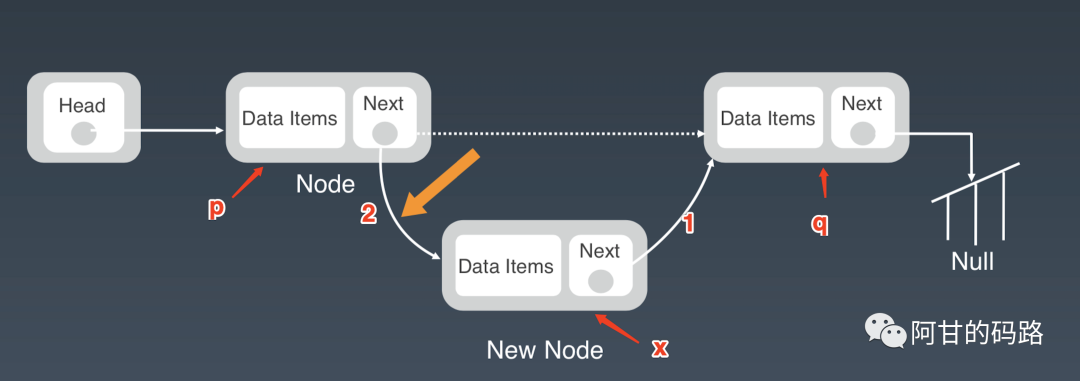
注意点：防止指针丢失和内存泄漏

“=”是赋值，习惯性从右往左读，例插入之前是 p->next = q，q 赋值给 p->next。

错误实现：

p->next = x; // 将p的next指针指向x结点;
x->next = p->next; // 将x的结点的next指针指向b结点;

第一步之后p->next = x，p->next指向了x结点，第二步相当于将 x赋值给 x->next，即相当于x->next = x，自己指向自己，显而易见的问题：q 的地址丢失了，从 q 往后的结点都访问不到，链表断成了两截。后面的地址弄丢了，JAVA有垃圾回收机制还好，C这样的语言程序员如果没有手动释放那些结点占的内存，就产生了内存泄漏，同时删除结点的时候如果不把结点的空间释放也会内存泄漏。

正确实现：

x->next = p->next; // 将x的结点的next指针指向b结点;
p->next = x; // 将p的next指针指向x结点;

顺序调换一下，先将q的地址存储好放到x结点，然后x结点再链接到p结点就好了。

这个问题开始重视起来是在大三找实习一家游戏公司总监问到，让我把这个地方再说一遍，我暗地里虎躯一震菊花一紧表面上却稳如泰山，最后用温柔的微笑让他如沐春风从而化解了这个尴尬，马上改口。

头插入

头插法

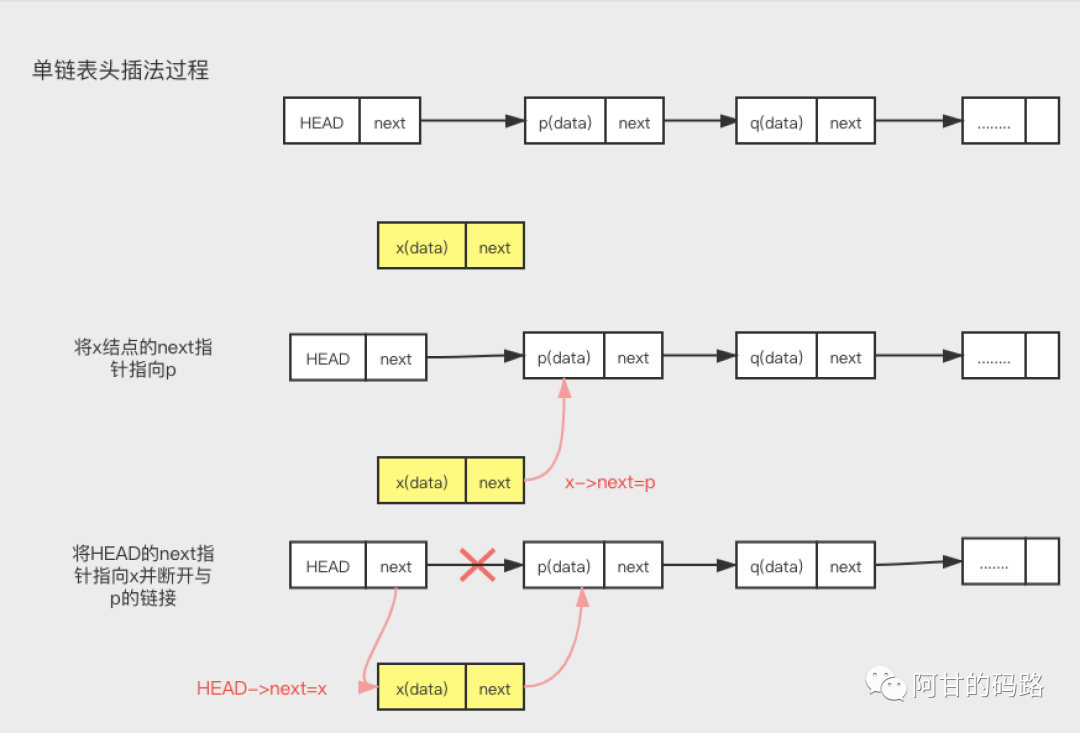
x->next = head->next; // 将x的结点的next指针指向b结点;
head->next = x; // 将p的next指针指向x结点;

可知有了头结点，头插入代码和中间插入代码是一样的，只不过上一个p结点变成了head 结点。

尾插入

尾插法

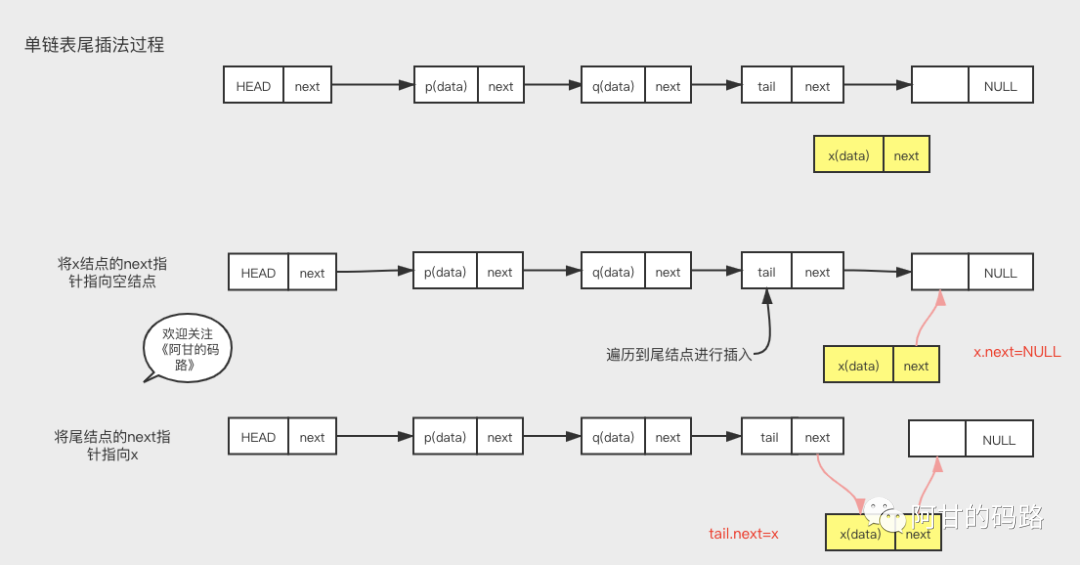
x.next = null;
tail.next = x;

头插法 VS 尾插法

HashMap 源码中，jdk8之前hash冲突时候用的都是头插法，jdk1.8之后用的尾插法，不知道你是否还有印象，主要原因是防止扩容的时候头插法造成链表环化，具体的读者有兴趣看看扩容源码。

头插法：遍历时候得到的数据顺序和插入的时候是相反的，原因是你第一次插进去的数据实际上成为了链表的尾巴；

尾插法：遍历得到的数据和插入的顺序是一致的。

删除结点

删除中间结点p

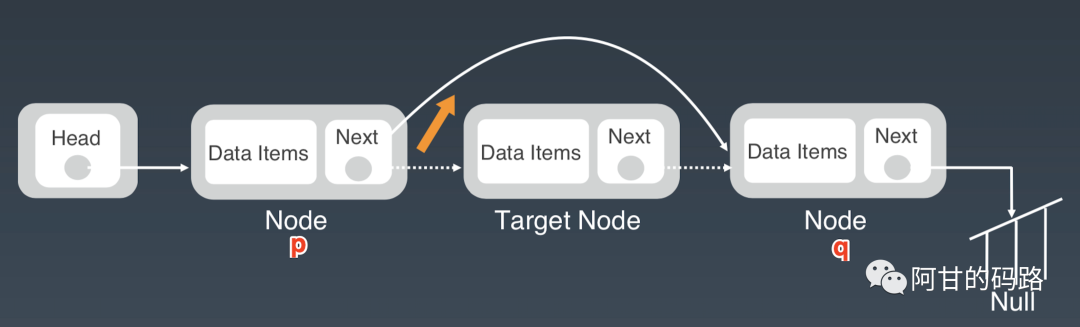
->next = p->next->next; 一行代码就可以

双向链表

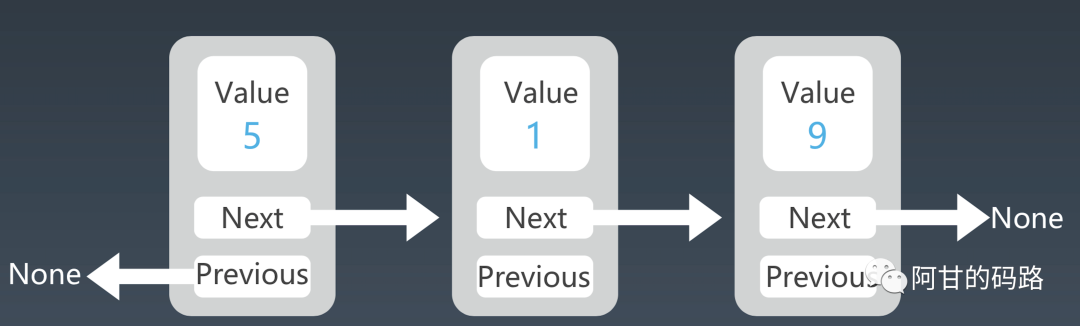
单链表的插入、删除操作的时间复杂度已经是O(1)了，为什么还要双向链表呢？优点在哪里。

还是从插入，删除，查找来看，拿删除操作来分析，无非两种情况：

删除给定指针指向的结点
删除结点中值等于xxx的结点

第二种，对于单链表和双链表都需要先进行遍历，直到找到值等于给定值的结点，然后删除；

第一种，区别就来了，我们已经找到了要删除的结点，但是删除某个结点q需要知道其前驱结点，单链表找前驱结点还是需要遍历先找到前驱结点，双链表就可以直接拿到前驱结点；

然后实际应用中，例如容器 HashMap，都是知道指针，第一种操作比较多，删除插入操作就是指针的操作，值都是动态变得不可能告诉你一个值再让你删除，所以这种结构的重要性不言而喻了，插入操作这里不再分析了。

循环链表

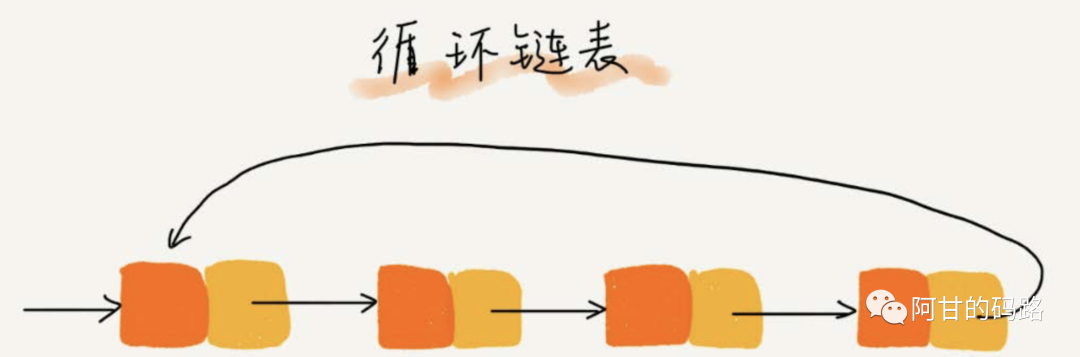
和单链表相比，循环链表的优点是从链尾到链头比较方便。当要处理的数据具有环型结构特点时，就特别适合采用循环链表。比如著名的约瑟夫问题。尽管用单链表也可以实现，但是用循环链表实现的话，代码就会简洁很多。

❝约瑟夫问题据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决？Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

❞

双向循环链表

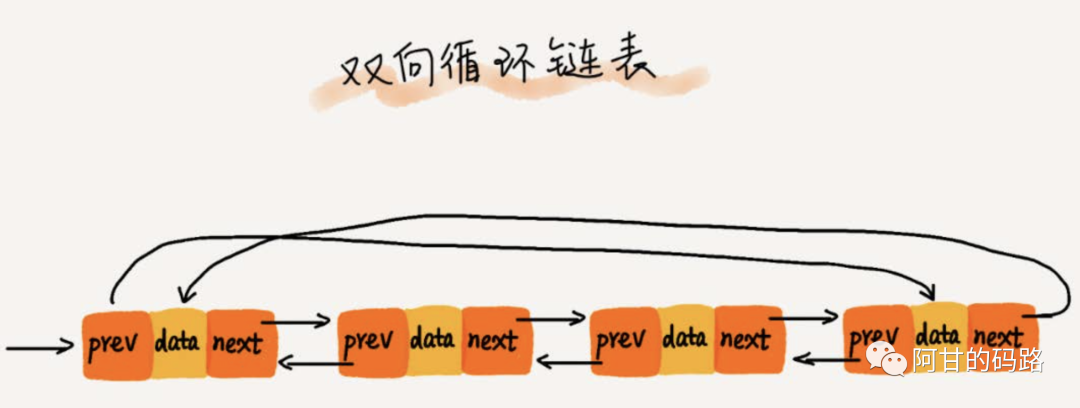双向循环链表 LinkedHashMap实现LRU缓存，源码解析（JDK1.8）

/**
 * A cache implementing a least recently used policy.
 */
public class LRUCache<K, V> implements Cache<K, V> {
    private final LinkedHashMap<K, V> cache;

    public LRUCache(final int maxSize) {
        cache = new LinkedHashMap<K, V>(16, .75f, true) {
            @Override
            protected boolean removeEldestEntry(Map.Entry<K, V> eldest) {
                return size() > maxSize;
            }
        };
    }
    方法伪代码：
    public V get(K key)
    public void put(K key, V value)
    public boolean remove(K key)
    public long size()    
}

可以得知 LRUCache 缓存就是使用 LinkedHashMap 结构实现的。

LinkedHashMap结构图

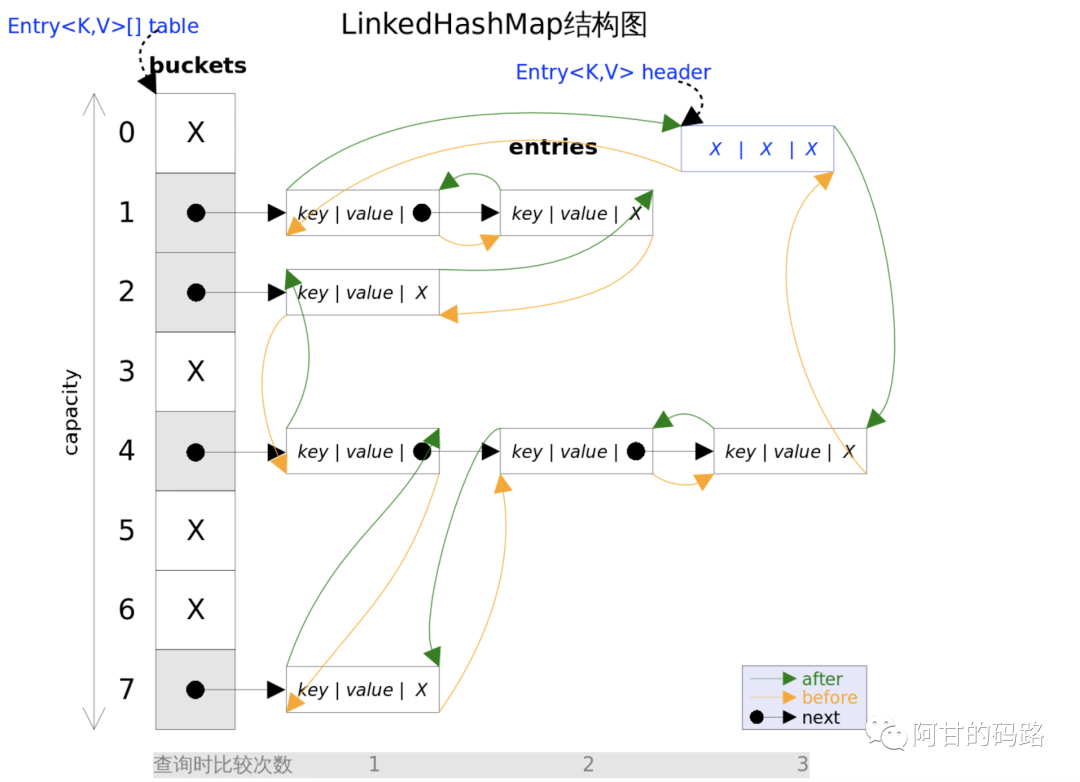
LinkedHashMap 继承了 HashMap（jdk1.8），总的结构还是数据+链表+红黑树，为了简化思想图里面没有红黑树的，就这样看哦；

public class LinkedHashMap<K,V>
    extends HashMap<K,V>
    implements Map<K,V>
{
    /**
     * HashMap.Node subclass for normal LinkedHashMap entries.
     */
    static class Entry<K,V> extends HashMap.Node<K,V> {
        Entry<K,V> before, after;
        Entry(int hash, K key, V value, Node<K,V> next) {
            super(hash, key, value, next);
        }
    }

    private static final long serialVersionUID = 3801124242820219131L;

    //双向链表头结点
    transient LinkedHashMap.Entry<K,V> head;

    //双向链表尾结点
    transient LinkedHashMap.Entry<K,V> tail;


    //如果accessOrder为flase的话，则按插入顺序来遍历，默认fasle
    /**
     true  基于访问顺序
    当accessOrder设置为true时，被访问的数据，将会被移到链表的尾部，put使用的也是尾插法；
同时get是从尾部开始访问，所以等于越常使用的数据，遍历的时间越短。
    **/
    final boolean accessOrder;

LRU 初始化启动 true

LRU 缓存初始化的时候，就用了这个 accessOrder，设置为true，从而最近被访问到的数据放到了链表末尾，链表前面的数据是长时间没有使用的，从链表末尾开始访问的话，链表头部开始的长久没有访问的数据就被淘汰掉了，从而实现LRU缓存。

Map 的 Entry 结点内容
static class Node<K,V> implements Map.Entry<K,V> {
        final int hash;
        final K key;
        V value;
        Node<K,V> next;

        Node(int hash, K key, V value, Node<K,V> next) {
            this.hash = hash;
            this.key = key;
            this.value = value;
            this.next = next;
        }
        ·······
}
// LinkedHashMap 的 Entry，可以看到比Map的结点多了两个指针 before,after
static class Entry<K,V> extends HashMap.Node<K,V> {
        Entry<K,V> before, after;
        Entry(int hash, K key, V value, Node<K,V> next) {
            super(hash, key, value, next);
        }
}

//生成一个新的结点
Node<K,V> newNode(int hash, K key, V value, Node<K,V> e) {
        LinkedHashMap.Entry<K,V> p =
            new LinkedHashMap.Entry<K,V>(hash, key, value, e);
        //结点尾插法放入链表最后
        linkNodeLast(p);
        return p;
    }

//尾插法，把新结点插入链表末尾
private void linkNodeLast(LinkedHashMap.Entry<K,V> p) {
    // 尾结点赋值给 last 指针
    LinkedHashMap.Entry<K,V> last = tail;
    // P 结点赋值给尾结点
    tail = p;
    // 如果尾部节点为空，说明是空链表，那么插入的就是第一个节点。这个时候新加入的数据赋给头部节点
    if (last == null)
        head = p;
    // 不是空链表，将新结点放到末尾    
    else {
        p.before = last;
        last.after = p;
    }
}

LinkedHashMap是继承的HashMap，插入删除都是直接用的HashMap的插入删除方法，只不过它重写了三个回调方法，来实现他需要的额外操作，如下：

// 在hashmap正常删除一个结点之后进行回调

void afterNodeRemoval(Node<K,V> e) { 
        /**定义了一个结点p，将传递进来的的e结点赋值给p，把传进来的e结点赋值给p结点，并且定义p的前驱结点b，后继结点a
 **/
        LinkedHashMap.Entry<K,V> p =
            (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
        p.before = p.after = null;
        // 如果前一个结点是null，那么这是个空链表
        if (b == null)
            head = a;
        else
            b.after = a;
        if (a == null)
            tail = b;
        else
            a.before = b;
    }

//在hashmap正常插入一个结点之后进行回调，插入一个结点可能缓存满了，因此需要移除最久没有使用的结点即第一个结点（前面讲了LRU的调度算法，不明白的可以回头去看）
/**
//根据evict,也就是前文linkedHashMap构造函数中的accessOrder，来判断是否删除双向链表中最老的元素，这个是实现lru需要用到的。
**/
void afterNodeInsertion(boolean evict) { // possibly remove eldest
        LinkedHashMap.Entry<K,V> first;
        if (evict && (first = head) != null && removeEldestEntry(first)) {
            K key = first.key;
            // hashmap的移除结点方法，传key第一个结点过去进行删除
            removeNode(hash(key), key, null, false, true);
        }
    }

// 最常用是hashmap正常putVal之后调用，将新加入的结点移动到链表末尾
void afterNodeAccess(Node<K,V> e) { // move node to last
        LinkedHashMap.Entry<K,V> last;
        if (accessOrder && (last = tail) != e) {
        // 把传进来的e结点赋值给p结点，并且定义p的前驱结点b，后继结点a
            LinkedHashMap.Entry<K,V> p =
                (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
            p.after = null;
            if (b == null)
                head = a;
            else
                b.after = a;
            if (a != null)
                a.before = b;
            else
                last = b;
            if (last == null)
                head = p;
            else {
                p.before = last;
                last.after = p;
            }
            // 把p结点赋值给尾结点
            tail = p;
            ++modCount;
        }
    }

afterNodeAccess()方法图解：

afterNodeAccess 方法图解

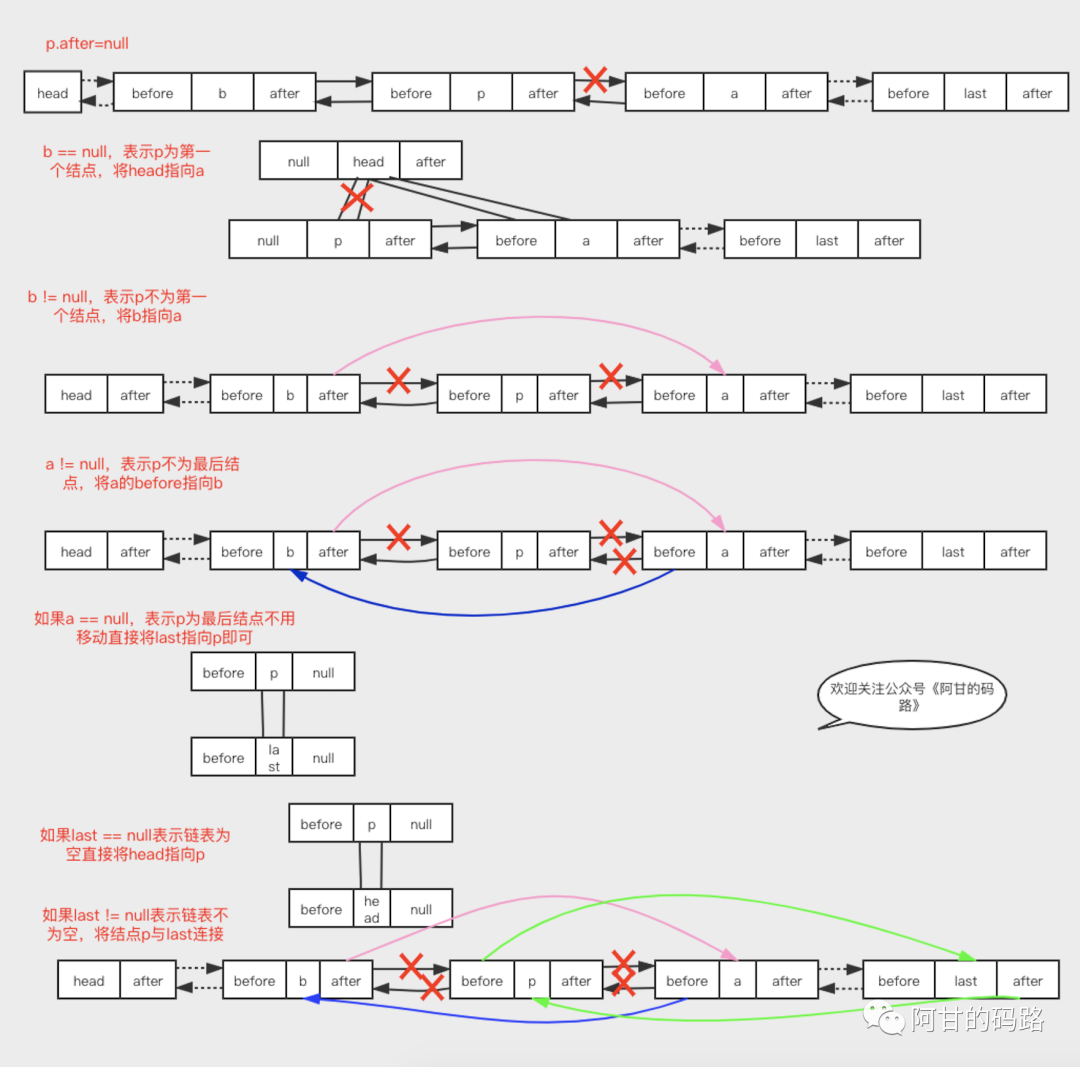
还是挺复杂的，画了一个多小时这张图。

算法爬楼梯

上一篇的遗留算法：

爬楼梯

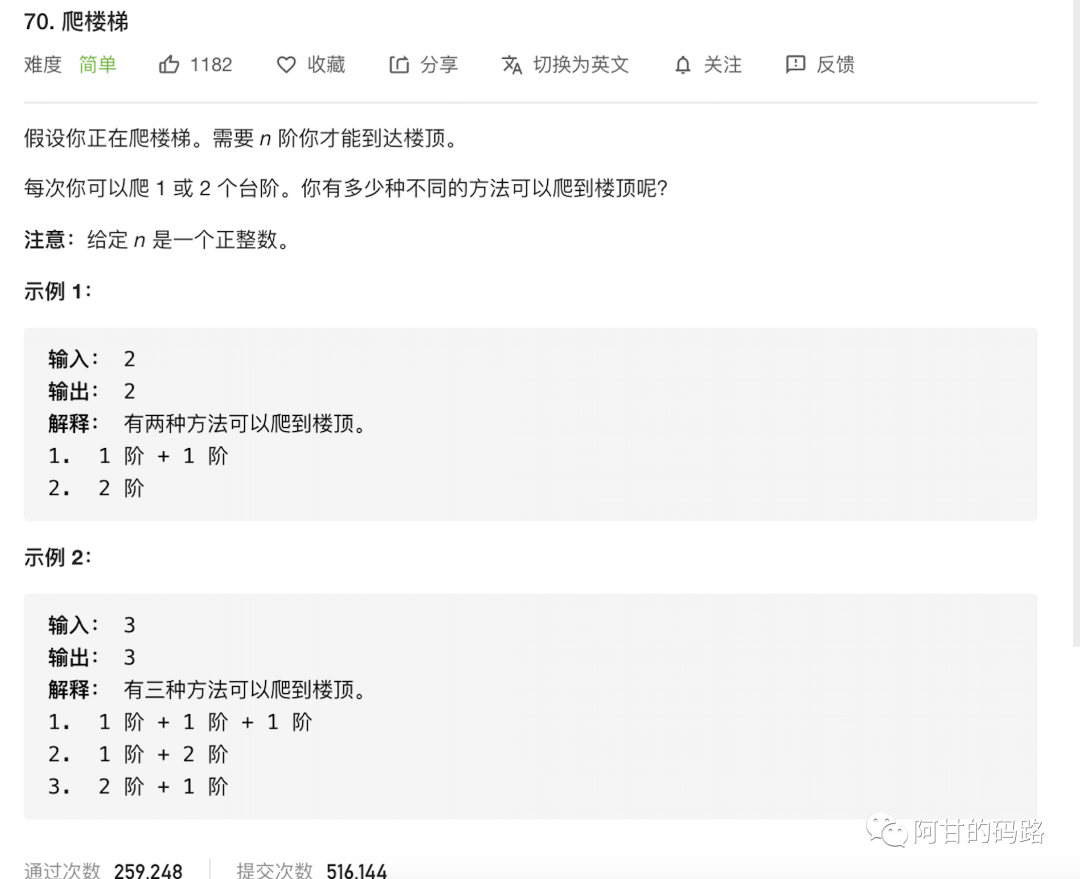
超哥说，「解决所有问题的法则」：

找最近重复的子问题；
为什么？因为写程序我们只能写if，else，for，while，recursion（递归）；
计算机是人类发明的，计算机肯定是没有人脑那么强的，它其实就是一个简单的重复式机器那么计算机运行的程序也是同理，它是用重复的东西来解决问题的；
如果我们遇到算法题的时候，就是需要我们用程序去解决的问题，那问题的本身就是可重复的；
无论是算法中的回溯、分治、动态规划、递归等，全部都是在找重复性的原理所以重点都是“找规律”；

分析问题：

刚刚拿到，没有思路，先暴力举例一阶（1种）：1

二阶（2种）：1+1，2

三阶（3种）：1+1+1，2+1，1+2 即二阶的走法+1和一阶的走法+2

四阶（5种）：1+1+1+1，1+2+1，2+1+1，1+1+2，2+2，即三阶的走法+1和二阶的走法+2，共五种

五阶（8种）：1+1+1+1+1，1+2+1，2+1+1，1+1+2+1，2+2+1，1+1+1+2，2+1+2，1+2+2 即四阶的走法+1和三阶的走法+2，共八种

......

思想：例如一共10阶，那么有两种方法，要不就是你走到了第八阶跨2步，或者走到第九阶了跨1步，再也没有别的实现了，因为你一次性只能跨两步或者一步，所以最终次数就是到达第八阶次数+到达第九阶的次数，f(10)=f(9)+f(8),每一层都是如此情况，即在上一个台阶走2步或者走1步到达终点，可知这其实是个斐波拉契问题。

「实现：」

1.斐波拉契，递归

    public static int climbStairs(int n) {
        if (n <= 1)
            return 1;
        if (n < 3)
            return n;
        return climbStairs(n - 1) + climbStairs(n - 2);
    }

但是这种方法，会一直递归，重复计算很多，例如我再代码里面打印一下就能看到：

重复计算

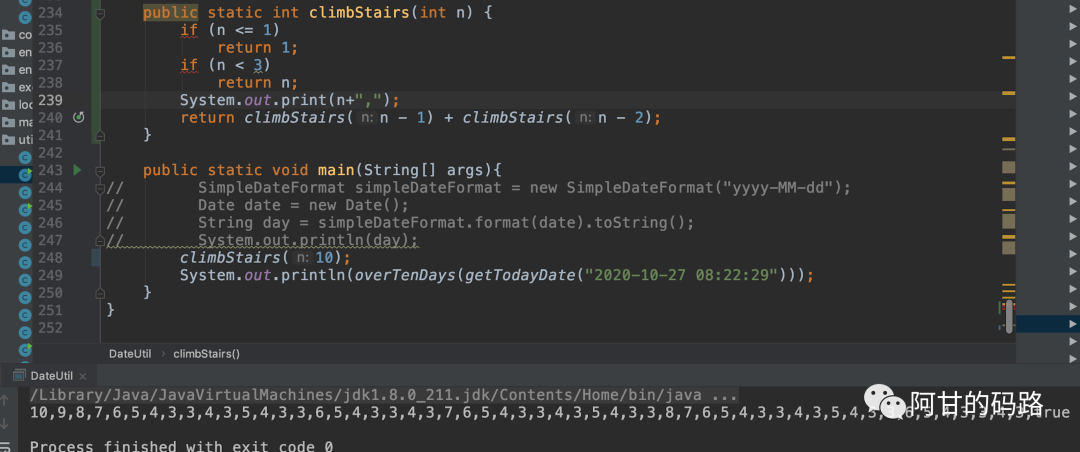
图解：

Fib6

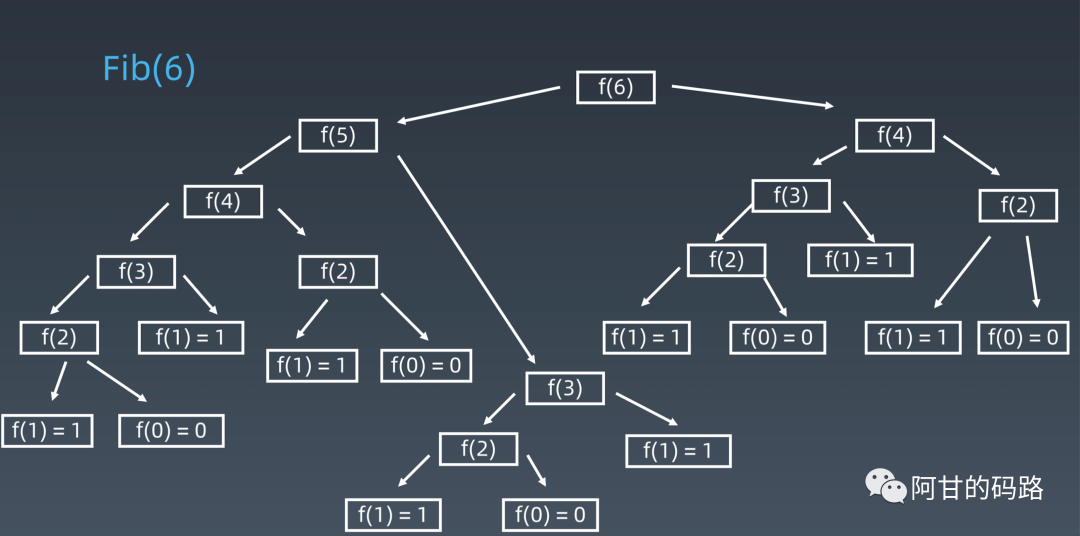
由图解可知，很多都被重复计算了多次，下面进行优化

2.循环

 public int climbStairs(int n) {
        if (n <= 1)
            return 1;
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }

用数组将每一阶的到达次数给存储，直接拿前面两个数据的和即可。

3.循环优化

可以不用数组存储每一阶的到达次数，直接定义两个变量就可以，节省了空间

4.公式实现

这个需要推导公式，非大佬不行，感兴趣自行百科。

算法反转链表

反转链表

算法链表环检测

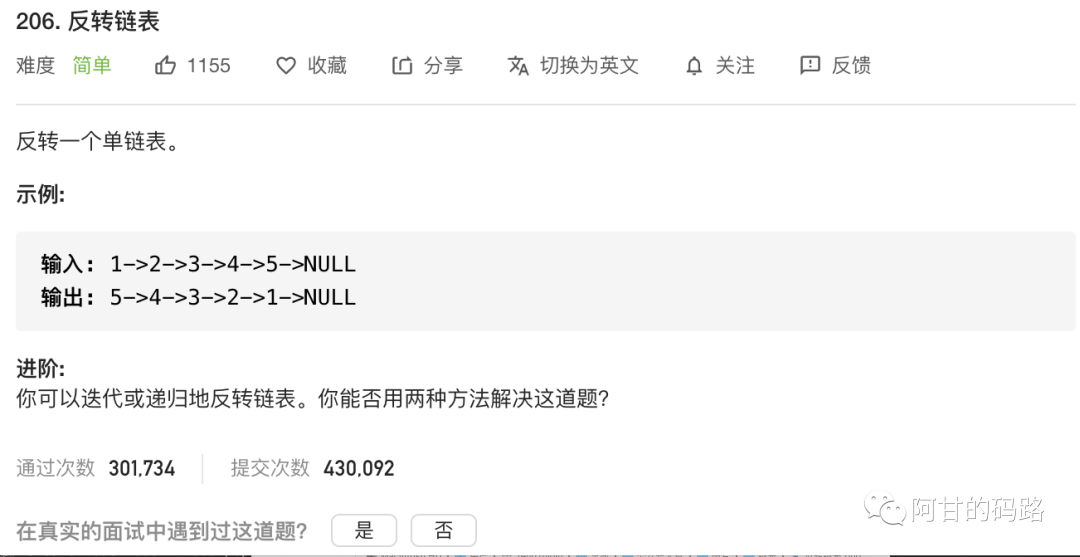
链表环检测

拿到题感觉是题目意图都很清晰，没有那么多花里胡哨的，但是真正要动笔还得掉些发，写这些用了洪荒之力了，下一篇再写这两题。