纯Javascript实现平滑曲线生成
前言
平滑曲线生成是一个很实用的技术。
很多时候,我们都需要通过绘制一些折线,然后让计算机平滑的连接起来,或者是生成一些平滑的面。
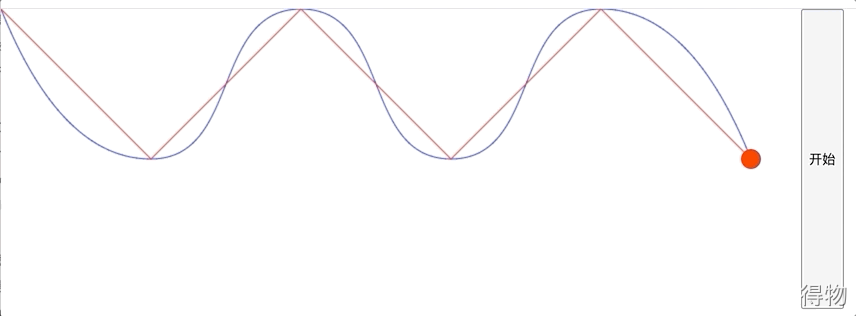
先来看下最终效果(红色为我们输入的直线,蓝色为拟合过后的曲线) 首尾可以特殊处理让图形看起来更好)。
贝塞尔曲线简介
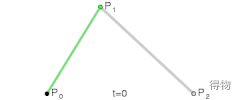
贝塞尔曲线(英语:Bézier curve)是计算机图形学中相当重要的参数曲线。
二次贝塞尔曲线
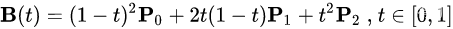
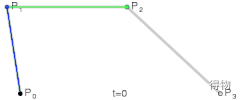
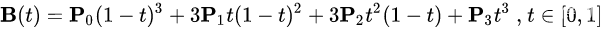
根据上面的公式我们可以得到计算函数。
二阶
/**
*
*
* @param {number} p0
* @param {number} p1
* @param {number} p2
* @param {number} t
* @return {*}
* @memberof Path
*/
bezier2P(p0: number, p1: number, p2: number, t: number) {
const P0 = p0 * Math.pow(1 - t, 2);
const P1 = p1 * 2 * t * (1 - t);
const P2 = p2 * t * t;
return P0 + P1 + P2;
}
/**
*
*
* @param {Point} p0
* @param {Point} p1
* @param {Point} p2
* @param {number} num
* @param {number} tick
* @return {*} {Point}
* @memberof Path
*/
getBezierNowPoint2P(
p0: Point,
p1: Point,
p2: Point,
num: number,
tick: number,
): Point {
return {
x: this.bezier2P(p0.x, p1.x, p2.x, num * tick),
y: this.bezier2P(p0.y, p1.y, p2.y, num * tick),
};
}
/**
* 生成二次方贝塞尔曲线顶点数据
*
* @param {Point} p0
* @param {Point} p1
* @param {Point} p2
* @param {number} [num=100]
* @param {number} [tick=1]
* @return {*}
* @memberof Path
*/
create2PBezier(
p0: Point,
p1: Point,
p2: Point,
num: number = 100,
tick: number = 1,
) {
const t = tick / (num - 1);
const points = [];
for (let i = 0; i < num; i++) {
const point = this.getBezierNowPoint2P(p0, p1, p2, i, t);
points.push({x: point.x, y: point.y});
}
return points;
}三阶
/**
* 三次方塞尔曲线公式
*
* @param {number} p0
* @param {number} p1
* @param {number} p2
* @param {number} p3
* @param {number} t
* @return {*}
* @memberof Path
*/
bezier3P(p0: number, p1: number, p2: number, p3: number, t: number) {
const P0 = p0 * Math.pow(1 - t, 3);
const P1 = 3 * p1 * t * Math.pow(1 - t, 2);
const P2 = 3 * p2 * Math.pow(t, 2) * (1 - t);
const P3 = p3 * Math.pow(t, 3);
return P0 + P1 + P2 + P3;
}
/**
* 获取坐标
*
* @param {Point} p0
* @param {Point} p1
* @param {Point} p2
* @param {Point} p3
* @param {number} num
* @param {number} tick
* @return {*}
* @memberof Path
*/
getBezierNowPoint3P(
p0: Point,
p1: Point,
p2: Point,
p3: Point,
num: number,
tick: number,
) {
return {
x: this.bezier3P(p0.x, p1.x, p2.x, p3.x, num * tick),
y: this.bezier3P(p0.y, p1.y, p2.y, p3.y, num * tick),
};
}
/**
* 生成三次方贝塞尔曲线顶点数据
*
* @param {Point} p0 起始点 { x : number, y : number}
* @param {Point} p1 控制点1 { x : number, y : number}
* @param {Point} p2 控制点2 { x : number, y : number}
* @param {Point} p3 终止点 { x : number, y : number}
* @param {number} [num=100]
* @param {number} [tick=1]
* @return {Point []}
* @memberof Path
*/
create3PBezier(
p0: Point,
p1: Point,
p2: Point,
p3: Point,
num: number = 100,
tick: number = 1,
) {
const pointMum = num;
const _tick = tick;
const t = _tick / (pointMum - 1);
const points = [];
for (let i = 0; i < pointMum; i++) {
const point = this.getBezierNowPoint3P(p0, p1, p2, p3, i, t);
points.push({x: point.x, y: point.y});
}
return points;
}拟合算法
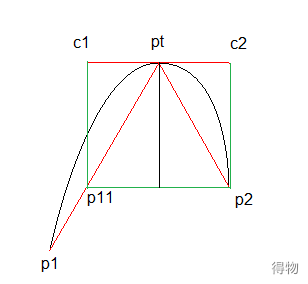
- 取p1-pt-p2的角平分线,c1c2垂直于该条角平分线c2为p2的投影点。
- 取短边作为c1-pt c2-pt的长度。
- 对该长度进行缩放,这个长度可以大概理解为曲线的弯曲程度。
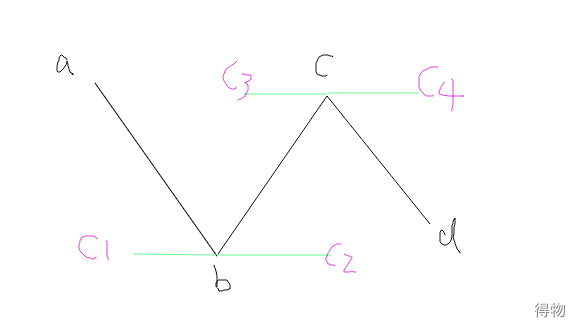
PS:这里可以按照个人想法处理。
bc线段:使用abc计算出来的控制点c2和bcd计算出来的控制点c3以此类推。
/**
* 生成平滑曲线所需的控制点
*
* @param {Vector2D} p1
* @param {Vector2D} pt
* @param {Vector2D} p2
* @param {number} [ratio=0.3]
* @return {*}
* @memberof Path
*/
createSmoothLineControlPoint(
p1: Vector2D,
pt: Vector2D,
p2: Vector2D,
ratio: number = 0.3,
) {
const vec1T: Vector2D = vector2dMinus(p1, pt);
const vecT2: Vector2D = vector2dMinus(p1, pt);
const len1: number = vec1T.length;
const len2: number = vecT2.length;
const v: number = len1 / len2;
let delta;
if (v > 1) {
delta = vector2dMinus(
p1,
vector2dPlus(pt, vector2dMinus(p2, pt).scale(1 / v)),
);
} else {
delta = vector2dMinus(
vector2dPlus(pt, vector2dMinus(p1, pt).scale(v)),
p2,
);
}
delta = delta.scale(ratio);
const control1: Point = {
x: vector2dPlus(pt, delta).x,
y: vector2dPlus(pt, delta).y,
};
const control2: Point = {
x: vector2dMinus(pt, delta).x,
y: vector2dMinus(pt, delta).y,
};
return {control1, control2};
}
/**
* 平滑曲线生成
*
* @param {Point []} points
* @param {number} ratio
* @return {*}
* @memberof Path
*/
createSmoothLine(points: Point[], ratio: number = 0.3) {
const len = points.length;
let resultPoints = [];
const controlPoints = [];
if (len < 3) return;
for (let i = 0; i < len - 2; i++) {
const {control1, control2} = this.createSmoothLineControlPoint(
new Vector2D(points[i].x, points[i].y),
new Vector2D(points[i + 1].x, points[i + 1].y),
new Vector2D(points[i + 2].x, points[i + 2].y),
ratio,
);
controlPoints.push(control1);
controlPoints.push(control2);
let points1;
let points2;
// 首端控制点只用一个
if (i === 0) {
points1 = this.create2PBezier(points[i], control1, points[i + 1], 50);
} else {
console.log(controlPoints);
points1 = this.create3PBezier(
points[i],
controlPoints[2 * i - 1],
control1,
points[i + 1],
50,
);
}
// 尾端部分
if (i + 2 === len - 1) {
points2 = this.create2PBezier(
points[i + 1],
control2,
points[i + 2],
50,
);
}
if (i + 2 === len - 1) {
resultPoints = [...resultPoints, ...points1, ...points2];
} else {
resultPoints = [...resultPoints, ...points1];
}
}
return resultPoints;
}案例代码
const input = [
{ x: 0, y: 0 },
{ x: 150, y: 150 },
{ x: 300, y: 0 },
{ x: 400, y: 150 },
{ x: 500, y: 0 },
{ x: 650, y: 150 },
]
const s = path.createSmoothLine(input);
let ctx = document.getElementById('cv').getContext('2d');
ctx.strokeStyle = 'blue';
ctx.beginPath();
ctx.moveTo(0, 0);
for (let i = 0; i < s.length; i++) {
ctx.lineTo(s[i].x, s[i].y);
}
ctx.stroke();
ctx.beginPath();
ctx.moveTo(0, 0);
for (let i = 0; i < input.length; i++) {
ctx.lineTo(input[i].x, input[i].y);
}
ctx.strokeStyle = 'red';
ctx.stroke();
document.getElementById('btn').addEventListener('click', () => {
let app = document.getElementById('app');
let index = 0;
let move = () => {
if (index < s.length) {
app.style.left = s[index].x - 10 + 'px';
app.style.top = s[index].y - 10 + 'px';
index++;
requestAnimationFrame(move)
}
}
move()
})