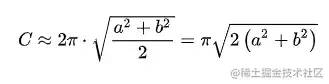【Web技术】1139- 手把手教你实现手绘风格图形

333次阅读  |  发布于3年以前

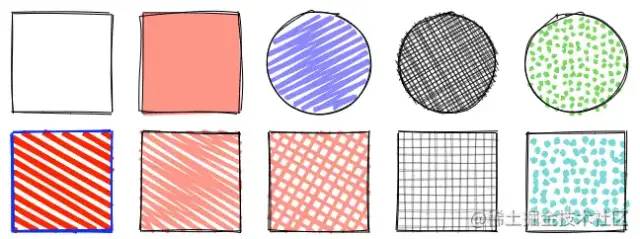
大家好，今天分享一篇高难度的图形绘制文章。Rough.js[1]是一个手绘风格的图形库，提供了一些基本图形的绘制能力，比如：

虽然笔者是个糙汉子，但是对这种可爱的东西都没啥抵抗力，这个库的使用本身很简单，没什么好说的，但是它只有绘制能力，没有交互能力，所以使用场景有限，先来用它画个示例图形：

import rough from 'roughjs/bundled/rough.esm.js'

this.rc = rough.canvas(this.$refs.canvas)
this.rc.rectangle(100, 150, 300, 200, {
    fillweight: 0,
    roughness: 3
})
this.rc.circle(195, 220, 40, {
    fill: 'red'
})
this.rc.circle(325, 220, 40, {
    fill: 'red'
})
this.rc.rectangle(225, 270, 80, 30, {
    fill: 'red',
    fillweight: 5
})
this.rc.line(200, 150, 150, 80, { roughness: 5 })
this.rc.line(300, 150, 350, 80, { roughness: 2 })

效果如下：

是不是有点蠢萌，本文的主要内容是带大家手动实现上面的图形，最终效果预览：lxqnsys.com/#/demo/hand…[2]。话不多说，代码见。

线段

万物基于线段，所以先来看线段怎么画，仔细看上图会发现手绘版线段其实是用两根弯曲的线段组成的，曲线可以使用贝塞尔曲线来画，这里使用三次贝塞尔曲线，那么剩下的问题就是求起点、终点、两个控制点的坐标了。贝塞尔曲线可以在这个网站上尝试：cubic-bezier.com/[3]。首先一条线段的起点和终点我们都给它加一点随机值，随机值比如就在[-2,2]之间，也可以把这个范围和线段的长度关联起来，比如线段越长，随机值就越大。

import rough from 'roughjs/bundled/rough.esm.js'

this.rc = rough.canvas(this.$refs.canvas)
this.rc.rectangle(100, 150, 300, 200, {
    fillweight: 0,
    roughness: 3
})
this.rc.circle(195, 220, 40, {
    fill: 'red'
})
this.rc.circle(325, 220, 40, {
    fill: 'red'
})
this.rc.rectangle(225, 270, 80, 30, {
    fill: 'red',
    fillweight: 5
})
this.rc.line(200, 150, 150, 80, { roughness: 5 })
this.rc.line(300, 150, 350, 80, { roughness: 2 })

接下来就是两个控制点，我们把控制点限定在线段所在的矩形内：

_line (x1, y1, x2, y2) {
    let result = []
    // 起始点
    // ...
    // 终点
    // ...
    // 两个控制点
    let xo = x2 - x1
    let yo = y2 - y1
    let randomFn = (x) => {
        return x > 0 ? this.random(0, x) : this.random(x, 0)
    }
    result[4] = x1 + randomFn(xo)
    result[5] = y1 + randomFn(yo)
    result[6] = x1 + randomFn(xo)
    result[7] = y1 + randomFn(yo)
    return result
}

然后把上面生成的曲线绘制出来：

// 绘制手绘线段
line (x1, y1, x2, y2) {
 this.drawDoubleLine(x1, y1, x2, y2)
}

// 绘制两条曲线
drawDoubleLine (x1, y1, x2, y2) {
    // 绘制生成的两条曲线
    let line1 = this._line(x1, y1, x2, y2)
    let line2 = this._line(x1, y1, x2, y2)
    this.drawLine(line1)
    this.drawLine(line2)
}

// 绘制单条曲线
drawLine (line) {
    this.ctx.beginPath()
    this.ctx.moveTo(line[0], line[1])
    // bezierCurveTo方法前两个点为控制点，第三个点为结束点
    this.ctx.bezierCurveTo(line[4], line[5], line[6], line[7], line[2], line[3])
    this.ctx.strokeStyle = '#000'
    this.ctx.stroke()
}

效果如下： 但是多试几次就会发现偏离太远、弯曲程度过大： 完全不像一个手正常的人能画出来的，去上面的贝塞尔曲线网站上试几次会发现两个控制点离线段越近，曲线弯曲程度越小： 所以我们要找线段附近的点作为控制点，首先随机一个横坐标点，然后可以计算出线段上该横坐标对应的纵坐标点，把该纵坐标点加减一点随机值即可。

_line (x1, y1, x2, y2) {
    let result = []
    // ...
    // 两个控制点
    let c1 = this.getNearRandomPoint(x1, y1, x2, y2)
    let c2 = this.getNearRandomPoint(x1, y1, x2, y2)
    result[4] = c1[0]
    result[5] = c1[1]
    result[6] = c2[0]
    result[7] = c2[1]
    return result
}

// 计算两个点连成的线段上附近的一个随机点
getNearRandomPoint (x1, y1, x2, y2) {
    let xo, yo, rx, ry
    // 垂直x轴的线段特殊处理
    if (x1 === x2) {
        yo = y2 - y1
        rx = x1 + this.random(-2, 2)// 在横坐标附近找一个随机点
        ry = y1 + yo * this.random(0, 1)// 在线段上找一个随机点
        return [rx, ry]
    }
    xo = x2 - x1
    rx = x1 + xo * this.random(0, 1)// 找一个随机的横坐标
    ry = ((rx - x1) * (y2 - y1)) / (x2 - x1) + y1// 通过两点式求出直线方程
    ry += this.random(-2, 2)// 纵坐标加一点随机值
    return [rx, ry]
}

看一下效果： 当然和Rough.js比起来还是不够好，有兴趣的可以自行去看一下源码，反正笔者是看不懂，控制变量太多，还没有注释。

多边形&矩形

多边形就是把多个点首尾相连起来，遍历顶点调用绘制线段的方法即可：

// 绘制手绘多边形
polygon (points = [], opt = {}) {
    if (points.length < 3) {
        return
    }
    let len = points.length
    for (let i = 0; i < len - 1; i++) {
        this.line(points[i][0], points[i][1], points[i + 1][0], points[i + 1][1])
    }
    // 首尾相连
    this.line(points[len - 1][0], points[len - 1][1], points[0][0], points[0][1])
}

矩形是多边形的一种特殊情况，四个角都是直角，一般传参为左上角顶点的x坐标、y坐标、矩形的宽、矩形的高：

// 绘制手绘矩形
rectangle (x, y, width, height, opt = {}) {
    let points = [
        [x, y],
        [x + width, y],
        [x + width, y + height],
        [x, y + height]
    ]
    this.polygon(points, opt)
}

image-20210207161756507.png

圆

圆要怎么处理呢，首先大家都知道圆是可以使用多边形来近似得到的，只要多边形的边足够多，那么看起来就足够圆，既然不想要太圆，那就把它恢复成多边形好了，多边形上面已经讲过了。恢复成多边形很简单，比如我们要把一个圆变成十边形（具体还原成几边形你也可以和圆的周长关联起来），那么每个边对应的弧度就是2*Math.PI/10，然后使用Math.cos和Math.sin来计算顶点的位置，最后再调用绘制多边形的方法进行绘制：

// 绘制手绘圆
circle (x, y, r) {
    let stepCount = 10
    let step = (2 * Math.PI) / stepCount
    let points = []
    for (let angle = 0; angle < 2 * Math.PI; angle += step) {
        let p = [
            x + r * Math.cos(angle),
            y + r * Math.sin(angle)
        ]
        points.push(p)
    }
    this.polygon(points)
}

效果如下： 可以看到效果很一般，就算边的数量再多一点看起来也不像： 如果直接用正常的线段连起来，那完全就是个正经多边形了，肯定也不行，所以核心是把线段变成随机弧形，首先为了增加随机性，我们把圆的半径和各个顶点都加一点随机增量：

circle (x, y, r) {
    let stepCount = 10
    let step = (2 * Math.PI) / stepCount
    let points = []
    let rx = r + this.random(-r * 0.05, r * 0.05)
    let ry = r + this.random(-r * 0.05, r * 0.05)
    for (let angle = 0; angle < 2 * Math.PI; angle += step) {
        let p = [
            x + rx * Math.cos(angle) + this.random(-2, 2),
            y + ry * Math.sin(angle) + this.random(-2, 2)
        ]
        points.push(p)
    }
}

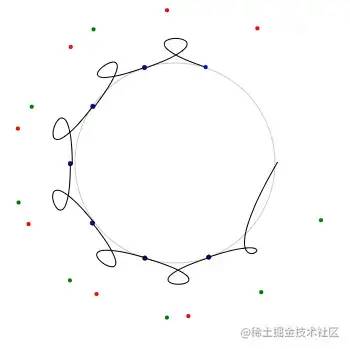
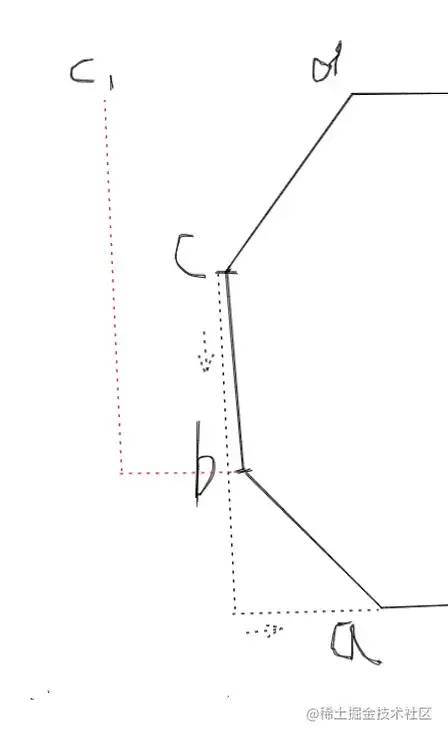
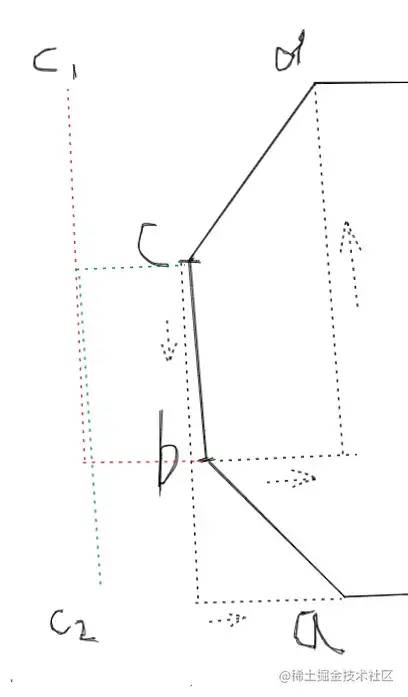
接下来的问题又变成了计算贝塞尔曲线的两个控制点，首先因为弧线肯定是要往多边形外凸的，根据贝塞尔曲线的性质，两个控制点一定是在线段的外面，直接用线段本身的两个端点来计算的话我试了一下，比较难处理，不同的角度可能都需要特殊处理，所以我们参考Rough.js间隔一个点： 比如上图的多边形我们随便找一个线段bc，对于点b来说上一个点是a，下一个点是c，b点分别加上c减a的横坐标纵坐标之差，得到了控制点c1，其他点也是一样，最后算出来的控制点都会在外面，现在还差一个控制点，我们不要让点c闲着，也给它加上前后两点之差： 可以看到点c的控制点c2和c1都在同一侧，这样画出来的曲线显然是朝一个方向的：

我们让它对称一下，让点c的前一个点减后一个点：

这样画出来的曲线仍然不行：

原因很简单，控制点离的太远了，所以我们少加一点差值，最后代码如下：

circle (x, y, r) {
    // ...
    let len = points.length
    this.ctx.beginPath()
    // 路径的起点移到第一个点
    this.ctx.moveTo(points[0][0], points[0][1])
    this.ctx.strokeStyle = '#000'
    for (let i = 1; i + 2 < len; i++) {
        let c1, c2, c3
        let point = points[i]
        // 控制点1
        c1 = [
            point[0] + (points[i + 1][0] - points[i - 1][0]) / 5,
            point[1] + (points[i + 1][1] - points[i - 1][1]) / 5
        ]
        // 控制点2
        c2 = [
            points[i + 1][0] + (point[0] - points[i + 2][0]) / 5,
            points[i + 1][1] + (point[1] - points[i + 2][1]) / 5
        ]
        c3 = [points[i + 1][0], points[i + 1][1]]
        this.ctx.bezierCurveTo(
            c1[0],
            c1[1],
            c2[0],
            c2[1],
            c3[0],
            c3[1]
        )
    }
    this.ctx.stroke()
}

我们只加差值的五分之一，我试了一下，5-7之间最自然，Rough.js加的是六分之一。

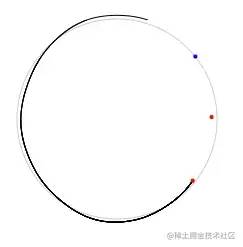
事情到这里并没有结束，首先这个圆还有个缺口，原因很简单，i + 2 < len的循环条件导致最后一个点没连上，另外首尾也没有相连，此外开头一段很不自然，太直了，原因是我们路径的起点是从第一个点开始的，但是我们的第一段曲线的结束点已经是第三个点了，所以先把路径的起点移到第二个点：

this.ctx.moveTo(points[1][0], points[1][1])

这样缺口就更大了：

红色的代表前两个点，蓝色的是最后一个点，为了要连到第二个点我们需要把顶点列表里的前三个点追加到列表最后：

// 把前三个点追加到列表最后
points.push([points[0][0], points[0][1]], [points[1][0], points[1][1]], [points[2][0], points[2][1]])
let len = points.length
this.ctx.beginPath()
// ...

效果如下：

问题又来了，应该没有人能徒手把圆的首尾完美无缺的连上，所以加的第二个点我们不能让它和原来的点一模一样，得加点偏移：

let end = [] // 处理最后一个连线点，让它和原本的点来点随机偏移
let radRandom = step * this.random(0.1, 0.5)// 让该点超前一点，代表画过头了，也可以来点负数，代表差一点才连上，但是比较丑
end[0] = x + rx * Math.cos(step + radRandom)// 要连的最后一个点实际上是列表里的第二个点，所以角度是step而不是0
end[1] = y + ry * Math.sin(step + radRandom)
points.push(
    [points[0][0], points[0][1]],
    [end[0], end[1]],
    [points[2][0], points[2][1]]
)
let len = points.length
this.ctx.beginPath()
//...

最后一个要优化的点是起点或者说终点位置，一般来说我们徒手画圆都是从上面开始画，因为0度是在x轴正轴方向，所以我们减去Math.PI/2左右就能把起点移到上方，最后完整的代码如下：

drawCircle (x, y, r) {
    // 圆变多边形
    let stepCount = 10
    let step = (2 * Math.PI) / stepCount// 多边形的一条边对应的角度
    let startOffset = -Math.PI / 2 + this.random(-Math.PI / 4, Math.PI / 4)// 起点偏移角度
    let points = []
    let rx = r + this.random(-r * 0.05, r * 0.05)
    let ry = r + this.random(-r * 0.05, r * 0.05)
    for (let angle = startOffset; angle < (2 * Math.PI + startOffset); angle += step) {
        let p = [
            x + rx * Math.cos(angle) + this.random(-2, 2),
            y + ry * Math.sin(angle) + this.random(-2, 2)
        ]
        points.push(p)
    }
    // 线段变曲线
    let end = [] // 处理最后一个连线点，让它和原本的点来点随机偏移
    let radRandom = step * this.random(0.1, 0.5)
    end[0] = x + rx * Math.cos(startOffset + step + radRandom)
    end[1] = y + ry * Math.sin(startOffset + step + radRandom)
    points.push(
        [points[0][0], points[0][1]],
        [end[0], end[1]],
        [points[2][0], points[2][1]]
    )
    let len = points.length
    this.ctx.beginPath()
    this.ctx.moveTo(points[1][0], points[1][1])
    this.ctx.strokeStyle = '#000'
    for (let i = 1; i + 2 < len; i++) {
        let c1, c2, c3
        let point = points[i]
        let num = 6
        c1 = [
            point[0] + (points[i + 1][0] - points[i - 1][0]) / num,
            point[1] + (points[i + 1][1] - points[i - 1][1]) / num
        ]
        c2 = [
            points[i + 1][0] + (point[0] - points[i + 2][0]) / num,
            points[i + 1][1] + (point[1] - points[i + 2][1]) / num
        ]
        c3 = [points[i + 1][0], points[i + 1][1]]
        this.ctx.bezierCurveTo(c1[0], c1[1], c2[0], c2[1], c3[0], c3[1])
    }
    this.ctx.stroke()
}

最后的最后，也可以和上面的线段一样画两次，综合效果如下：

圆搞定了，椭圆也类似，毕竟圆是椭圆的一种特殊情况，顺带提一下，椭圆的近似周长公式如下：

填充

样式1

先来看一种比较简单的填充：

上面我们绘制的矩形四条边是断开的，路径不闭合不能直接调用canvas的fill方法，所以需要把这四段曲线首尾连起来：

// 绘制手绘多边形
polygon (points = [], opt = {}) {
    if (points.length < 3) {
        return
    }
    // 加上填充方法
    let lines = this.closeLines(points)
    this.fillLines(lines, opt)

    // 描边
    let len = points.length
    // ...
}

closeLines方法用来把顶点闭合成曲线：

// 把多边形的顶点转换成首尾相连的闭合线段
closeLines (points) {
    let len = points.length
    let lines = []
    let lastPoint = null
    for (let i = 0; i < len - 1; i++) {
        // _line方法上文已经实现了，把直线段转换成曲线
        let arr = this._line(
            points[i][0],
            points[i][1],
            points[i + 1][0],
            points[i + 1][1]
        )
        lines.push([
            lastPoint ? lastPoint[2] : arr[0], // 上一个点存在则使用上一个点的终点来作为该点的起点
            lastPoint ? lastPoint[3] : arr[1],
            arr[2],
            arr[3],
            arr[4],
            arr[5],
            arr[6],
            arr[7]
        ])
        lastPoint = arr
    }
    // 首尾闭合
    let arr = this._line(
        points[len - 1][0],
        points[len - 1][1],
        points[0][0],
        points[0][1]
    )
    lines.push([
        lastPoint ? lastPoint[2] : arr[0],
        lastPoint ? lastPoint[3] : arr[1],
        lines[0][0], // 终点是第一条线段的起点
        lines[0][1],
        arr[4],
        arr[5],
        arr[6],
        arr[7]
    ])
    return lines
}

线段有了，只要遍历线段绘制出来最后调用fill方法即可：

// 填充多边形
fillLines (lines, opt) {
    this.ctx.beginPath()
    this.ctx.fillStyle = opt.fillStyle
    for (let i = 0; i + 1 < lines.length; i++) {
        let line = lines[i]
        if (i === 0) {
            this.ctx.moveTo(line[0], line[1])
        }
        this.ctx.bezierCurveTo(
            line[4],
            line[5],
            line[6],
            line[7],
            line[2],
            line[3]
        )
    }
    this.ctx.fill()
}

效果如下：

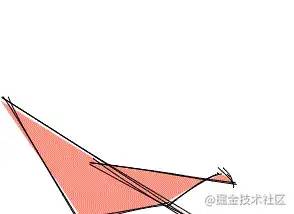
圆就更简单了，本身差不多就是闭合的，只要我们把最后一个点的特殊处理逻辑给去掉就行了：

// 下面几行代码都给去掉，使用原本的点即可
let end = []
let radRandom = step * this.random(0.1, 0.5)
end[0] = x + rx * Math.cos(startOffset + step + radRandom)
end[1] = y + ry * Math.sin(startOffset + step + radRandom)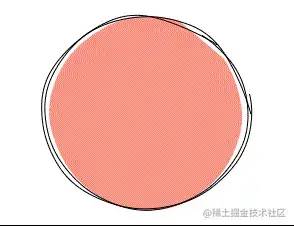

2021-03-19-14-54-42.gif

样式2

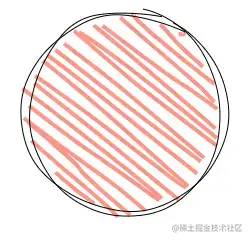
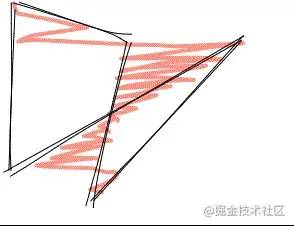
第二种填充会稍微复杂一点，比如下面这种最简单的填充，其实就是一些倾斜的线段，但问题是这些线段的端点怎么确定，矩形当然可以暴力的算出来，但是不规则的多边形怎么办，所以需要找到一个通用的方法。

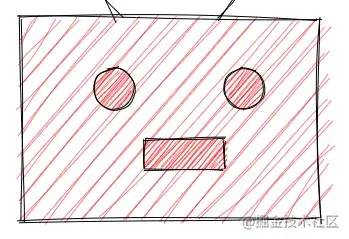
填充最暴力的方法就是判断每个点是否在多边形内部，但是这样的计算量太大，我查了一下多边形填充的思路，大概有两种算法：扫描线填充和种子填充，扫描线填充更流行，Rough.js用的也是这种方法，所以接下来介绍一下这个算法。扫描线填充很简单，就是一条扫描线（水平线）从多边形的底部开始往上扫描，那么每条扫描线都会和多边形有交点，同一条扫描线和多边形的各个交点之间的区域就是我们要填充的，那么问题来了，怎么确定交点，以及怎么判断两个交点之间属于多边形内部。

关于交点的计算，首先我们交点的y坐标是已知的，就是扫描线的y坐标，那么只要求出x，知道线段的两个端点坐标，那么可以求出直线方程，然后再计算，但是有一种更简单的方法，就是利用边的相关性，也就是知道了线段上的某一点，其相邻的点可以轻松的根据该点求出，下面是推导过程：

// 设直线方程
y = kx + b
// 设两点：c(x3, y3)，d点的y坐标为c点y坐标+1，d（x4, y3 + 1），那么要求出x4
y3 = kx3 + b// 1
y3 + 1 = kX4 + b// 2
// 1式代入2式
kx3 + b + 1 = kX4 + b
kx3 + 1 = kX4// 约去b
X4 = x3 + 1 / k// 两边同时除k
// 所以y坐标+1，x坐标为上一个点的x坐标加上直线斜率的倒数
// 多边形的线段是已知两个点的，假设为a（x1, y1）、b（x2, y2）,那么斜率k如下：
k = (y2 - y1) / 
// 斜率的倒数也就是
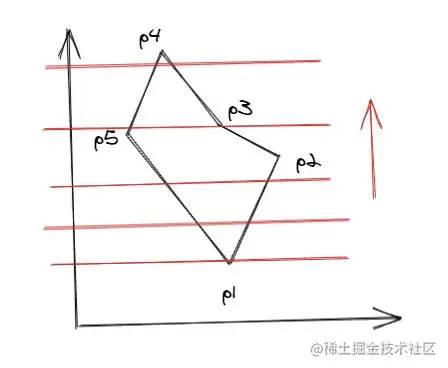
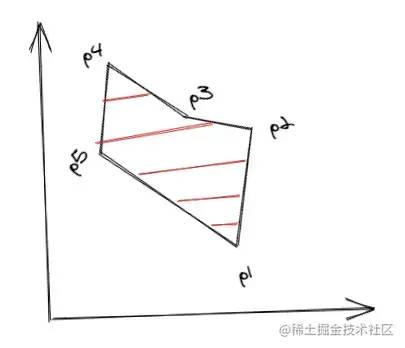
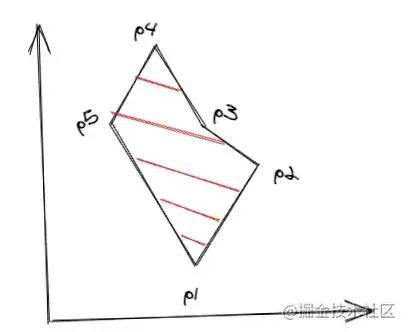
1/k = (x2 - x1) / (y2 - y1)

这样我们从线段的一个端点开始，可以挨个计算出线段上的所有点。详细的算法介绍和推导过程可以看一下这个PPT：wenku.baidu.com/view/4ee141…[4]，接下来直接来看算法的实现过程。先简单介绍一下几个名词：1.边表ET边表ET，一个数组，里面保存了多边形所有边的信息，每条边保存的信息有：该边y的最大值ymax和最小值ymin、该边最低点的x值xi、该边斜率的倒数dx。边按ymin递增排序，ymin相同则按xi递增，xi也相同则只能看ymax，如果ymax还相同，说明两条边重合了，如果不重合，则按yamx递增排序。2.活动边表AET也是一个数组，里面保存着与当前扫描线相交的边信息，随着扫描线的扫描会发生变化，删除不相交的，添加新相交的。该表里的边按xi递增排序。比如下面的多边形ET表顺序为：

// ET
[p1p5, p1p2, p5p4, p2p3, p4p3]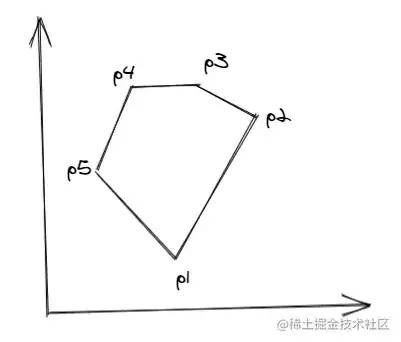

下面是具体的算法步骤：1.根据多边形的顶点数据创建ET表edgeTable，按上述顺序排序；2.创建一个空的AET表activeEdgeTable；3.开始扫描，扫描线的y=多边形的最低点的y值，也就是activeEdgeTable[0].ymin；4.重复下面步骤，直到ET表和AET表都为空：(1)从ET表里取出与当前扫描线相交的边，添加到AET表里，同样按上面提到的顺序排序 (2)成对取出AET表里的边信息的xi值，在每对之间进行填充 (3)从AET表里删除当前已经扫描到最后的边，即y >= ymax (4)更新AET表里剩下的边信息的xi，即xi = xi + dx (5)更新扫描线的y，即y = y + 1看着并不难，接下来转化成代码，先创建一下边表ET：

// 创建排序边表ET
createEdgeTable (points) {
    // 边表ET
    let edgeTable = []
    // 将第一个点复制一份到队尾，用来闭合多边形
    let _points = points.concat([[points[0][0], points[0][1]]])
    let len = _points.length
    for (let i = 0; i < len - 1; i++) {
        let p1 = _points[i]
        let p2 = _points[i + 1]
        // 过滤掉平行于x轴的线段，详见上述PPT链接
        if (p1[1] !== p2[1]) {
            let ymin = Math.min(p1[1], p2[1])
            edgeTable.push({
                ymin,
                ymax: Math.max(p1[1], p2[1]),
                xi: ymin === p1[1] ? p1[0] : p2[0], // 最低顶点的x值
                dx: (p2[0] - p1[0]) / (p2[1] - p1[1]) // 线段的斜率的倒数
            })
        }
    }
    // 对边表进行排序
    edgeTable.sort((e1, e2) => {
        // 按ymin递增排序
        if (e1.ymin < e2.ymin) {
            return -1
        }
        if (e1.ymin > e2.ymin) {
            return 1
        }
        // ymin相同则按xi递增
        if (e1.xi < e2.xi) {
            return -1
        }
        if (e1.xi > e2.xi) {
            return 1
        }
        // xi也相同则只能看ymax
        // ymax还相同，说明两条边重合
        if (e1.ymax === e2.ymax) {
            return 0
        }
        // 如果不重合，则按yamx递增排序
        if (e1.ymax < e2.ymax) {
            return -1
        }
        if (e1.ymax > e2.ymax) {
            return 1
        }
    })
    return edgeTable
}

接下来进行扫描操作：

scanLines (points) {
    if (points.length < 3) {
        return []
    }
    let lines = []
    // 创建排序边表ET
    let edgeTable = this.createEdgeTable(points)
    // 活动边表AET
    let activeEdgeTable = []
    // 开始扫描，从多边形的最低点开始
    let y = edgeTable[0].ymin
    // 循环的终点是两个表都为空
    while (edgeTable.length > 0 || activeEdgeTable.length > 0) {
        // 从ET表里把当前扫描线的边添加到AET表里
        if (edgeTable.length > 0) {
            // 将当前ET表里和扫描线相交的边添加到AET表里
            for (let i = 0; i < edgeTable.length; i++) {
                // 如果扫描线的间隔加大，可能高低差比较小的线段会被整个直接跳过，导致死循环，需要考虑到这种情况
                if (edgeTable[i].ymin <= y && edgeTable[i].ymax >= y || edgeTable[i].ymax < y) {
                    let removed = edgeTable.splice(i, 1)
                    activeEdgeTable.push(...removed)
                    i--
                }
            }
        }
        // 从AET表里删除y=ymax的记录
        activeEdgeTable = activeEdgeTable.filter((item) => {
            return y < item.ymax
        })
        // 按xi从小到大排序
        activeEdgeTable.sort((e1, e2) => {
            if (e1.xi < e2.xi) {
                return -1
            } else if (e1.xi > e2.xi) {
                return 1
            } else {
                return 0
            }
        })
        // 如果存在活动边，则填充活动边之间的区域
        if (activeEdgeTable.length > 1) {
            // 每次取两个边出来进行填充
            for (let i = 0; i + 1 < activeEdgeTable.length; i += 2) {
                lines.push([
                    [Math.round(activeEdgeTable[i].xi), y],
                    [Math.round(activeEdgeTable[i + 1].xi), y]
                ])
            }
        }
        // 更新活动边的xi
        activeEdgeTable.forEach((item) => {
            item.xi += item.dx
        })
        // 更新扫描线y
        y += 1
    }
    return lines
}

代码其实就是上述算法过程的翻译，理解了算法代码并不难理解，在多边形方法里调用一下该方法：

// 绘制手绘多边形
polygon (points = [], opt = {}) {
    if (points.length < 3) {
        return
    }
    // 加上填充方法
    let lines = this.scanLines(points)
    lines.forEach((line) => {
        this.drawDoubleLine(line[0][0], line[0][1], line[1][0], line[1][1], {
            color: opt.fillStyle
        })
    })

    // 描边
    let len = points.length
    // ...
}

看一下最后的填充效果：

效果已经出来了，但是太密了，因为我们的扫描线每次加的是1，我们多加点试试：

scanLines (points) {
    // ...

    // 我们让扫描线每次加10
    let gap = 10
    // 更新活动边的xi
    activeEdgeTable.forEach((item) => {
        item.xi += item.dx * gap// 斜率的倒数为什么也要乘10可以去看上面的推导过程
    })
    // 更新扫描线y
    y += gap

    // ...
}

顺便也加粗一下线段的宽度，效果如下：

也可以把线段的首尾交替相连变成一笔画的效果：

具体实现可以去源码里看，接下来我们看最后一个问题，就是让填充线倾斜一点角度，目前都是水平的。填充线想要倾斜首先我们可以让图形先旋转一定角度，这样扫描出来的线还是水平的，然后再让图形和填充线一起再旋转回去就得到倾斜的线了。

上图表示图形逆时针旋转后进行扫描，下图表示图形和填充线顺时针旋转回去。

图形旋转也就是各个顶点旋转，所以问题就变成了求一个点旋转指定角度后的位置，下面来推导一下。

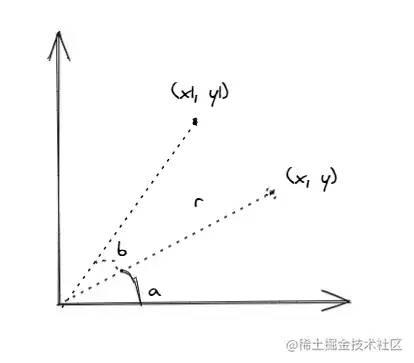
上图里点(x,y)原本的角度为a，线段长为r，求旋转角度b后的坐标(x1,y1)：

x = Math.cos(a) * r// 1
y = Math.sin(a) * r// 2

x1 = Math.cos(a + b) * r
y1 = Math.sin(a + b) * r

// 把cos(a+b)、sin(a+b)展开
x1 = (Math.cos(a) * Math.cos(b) - Math.sin(a) * Math.sin(b)) * r// 3
y1 = (Math.sin(a) * Math.cos(b) + Math.cos(a) * Math.sin(b)) * r// 4

// 把1式和2式代入3式和4式
Math.cos(a) = x / r
Math.sin(a) = y / r
x1 = ((x / r) * Math.cos(b) - (y / r) * Math.sin(b)) * r
y1 = ((y / r) * Math.cos(b) + (x / r) * Math.sin(b)) * r
// 约去r
x1 = x * Math.cos(b) - y * Math.sin(b)
y1 = y * Math.cos(b) + x * Math.sin(b)

由此可以得到求一个点旋转指定角度后的坐标的函数：

getRotatedPos (x, y, rad) {
    return [
        x: x * Math.cos(rad) - y * Math.sin(rad),
        y: y * Math.cos(rad) + x * Math.sin(rad)
    ]
}

有了该函数我们就可以来旋转多边形了：

// 绘制手绘多边形
polygon (points = [], opt = {}) {
    if (points.length < 3) {
        return
    }
    // 扫描前先旋转多边形
    let _points = this.rotatePoints(points, opt.rotate)
    let lines = this.scanLines(_points)
    // 扫描完得到的线段我们再旋转相反的角度
    lines = this.rotateLines(lines, -opt.rotate)
    lines.forEach((line) => {
        this.drawDoubleLine(line[0][0], line[0][1], line[1][0], line[1][1], {
            color: opt.fillStyle
        })
    })

    // 描边
    let len = points.length
    // ...
}

// 旋转顶点列表
rotatePoints (points, rotate) {
    return points.map((item) => {
        return this.getRotatedPos(item[0], item[1], rotate)
    })
}

// 旋转线段列表
rotateLines (lines, rotate) {
    return lines.map((line) => {
        return [
            this.getRotatedPos(line[0][0], line[0][1], rotate),
            this.getRotatedPos(line[1][0], line[1][1], rotate)
        ]
    })
}

效果如下：

圆形也是一样，转换成多边形后先旋转，然后扫描再旋转回去：

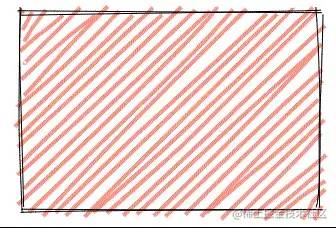
总结

本文介绍了几种简单图形的手绘风格实现方法，其中涉及到了简单的数学知识及区域填充算法，如果有不合理或更好的实现方式请在留言区讨论吧，完整的示例代码在：github.com/wanglin2/ha…[5]。感谢阅读，下次再会~参考文章：

参考资料

[1]https://roughjs.com/

[2]http://lxqnsys.com/#/demo/handPaintedStyle

[3]https://cubic-bezier.com

[4]https://wenku.baidu.com/view/4ee141347c1cfad6195fa7c9.html

[5]https://github.com/wanglin2/handPaintedStyle

Copyright© 2013-2020

All Rights Reserved 京ICP备2023019179号-8