一道面试题引起的...

引言--面试题

有个结构体如下:

struct AdItem {
  std::string ad_id; // 广告id
  int priority; // 优先级
  int score; // 得分
};

现在有一个AdItem类型的verctor，要求对其排序

排序规则如下:

1、按照priority升序排列

2、如果priority一样大，则按照score降序排列

3、如果score也一样，则随机排序

void ad_sort(vector<AdItem> &ad_items) {

std::sort(ad_items.begin(), ad_items.end(), [](const AdItem &item1, const AdItem &item2) {
  if (item1.priority < item2.priorty) {
      return true;
    } else if (item1.priority > item2.priorty) {
      return false;
    } else {
    if (item1.score > item2.score) {
      return true;
    } else if (item1.score < item2.score) {
      return false;
    } else {
      return rand() % 2 == 0 ? true : false;
    }
    }
} );
}

STL中sort实现

我们先说结论：

在STL的sort中，在数据量大时候，采用快排，分段递归排序。一旦分段后的数据量小于某个阈值，为了避免快排的递归调用引起的额外开销，此时就采用插入排序。如果递归层次过深，还会采用堆排序。

下面我们将对STL中的sort实现进行深入讲解。

template <class _RandomAccessIter, class _Compare>

inline void sort(_RandomAccessIter __first, _RandomAccessIter __last,
                 _Compare __comp) {
 ...
  if (__first != __last) {
    __introsort_loop(__first, __last,
                     __VALUE_TYPE(__first),
                     __lg(__last - __first) * 2,
                     __comp);
    __final_insertion_sort(__first, __last, __comp);
  }
}

它是一个模板函数，只接受随机访问迭代器。if语句先判断区间有效性，接着调用__introsort_loop，它就是STL的Introspective Sort（内省式排序）实现。在该函数结束之后，最后调用插入排序。

在此，我们需要注意的一点是，在STL的内省式排序中，depth_limit 的初始值是__lg(__last - __first) * 2,即 2 * lg(__last - __first)

下面我们来详细分析该函数。

__introsort_loop

template <class _RandomAccessIter, class _Tp, class _Size, class _Compare>

void __introsort_loop(_RandomAccessIter __first,
                      _RandomAccessIter __last, _Tp*,
                      _Size __depth_limit, _Compare __comp)
{
  while (__last - __first > __stl_threshold) {
    if (__depth_limit == 0) {
      partial_sort(__first, __last, __last, __comp);
      return;
    }
    --__depth_limit;
    _RandomAccessIter __cut =
      __unguarded_partition(__first, __last,
                            _Tp(__median(*__first,
                                         *(__first + (__last - __first)/2),
                                         *(__last - 1), __comp)),
       __comp);
    __introsort_loop(__cut, __last, (_Tp*) 0, __depth_limit, __comp);
    __last = __cut;
  }
}

为了更清楚的理解该函数的功能，我们先将该函数中的调用子函数讲解，最后，通过逐个将子函数串起来，进行讲解该函数。

全局变量__stl_threshold

其定义如下：

const int __stl_threshold = 16;

数据最小分段阈值。当数据长度小于该阈值时，再使用递归来排序显然不划算，递归的开销相对来说太大。而此时整个区间内部有多个元素个数少于16的子序列，每个子序列都有相当程度的排序，但又尚未完全排序，过多的递归调用是不可取的。而这种情况刚好插入排序最拿手，它的效率能够达到O(N)。因此这里中止快速排序，sort会接着调用外部的__final_insertion_sort，即插入排序来处理未排序完全的子序列。

__lg

template <class _Size>

inline _Size __lg(_Size __n) {
  _Size __k;
  for (__k = 0; __n != 1; __n >>= 1) ++__k;
  return __k;
}

该函数主要功能是找出2^k <= n的最大k。当n = 7的时候，k = 2；当n = 20的时候，k = 4；当n = 8的时候，k = 3。

参数 depth_limit 由该函数获取。每次都会自减一次；当该参数为 0 时，意味着递归深度已经很深，很可能快排掉入了陷阱，因此调用堆排，并退出递归。

partial_sort

堆排序。

前面有提到，由depth_limit来决定是否进入堆排序。当递归次数超过depth_limit时，函数调用partial_sort。此时采用堆排序可以将快速排序的效率从O(N2)提升到O(N logN)，杜绝了过度递归所带来的开销。堆排序结束之后直接结束当前递归。

template <class _RandomAccessIter, class _Compare>

inline void partial_sort(_RandomAccessIter __first,
                         _RandomAccessIter __middle,
                         _RandomAccessIter __last, _Compare __comp) {
  __STL_REQUIRES(_RandomAccessIter, _Mutable_RandomAccessIterator);
  __STL_BINARY_FUNCTION_CHECK(_Compare, bool, 
      typename iterator_traits<_RandomAccessIter>::value_type,
      typename iterator_traits<_RandomAccessIter>::value_type);
  __partial_sort(__first, __middle, __last, __VALUE_TYPE(__first), __comp);
}
template <class _RandomAccessIter, class _Tp, class _Compare>

void __partial_sort(_RandomAccessIter __first, _RandomAccessIter __middle,
                    _RandomAccessIter __last, _Tp*, _Compare __comp) {
  make_heap(__first, __middle, __comp);
  for (_RandomAccessIter __i = __middle; __i < __last; ++__i)
    if (__comp(*__i, *__first))
      __pop_heap(__first, __middle, __i, _Tp(*__i), __comp,
                 __DISTANCE_TYPE(__first));
  sort_heap(__first, __middle, __comp);
}

快排

当去掉递归恶化的处理，introsort_loop函数，其实就是一个快排。快排的伪代码如下：

qsort(first, last):

    cut = partition(first, last, pivot)  // pivot is picked in [first, last)
    qsort(cut + 1, last)
    qsort(first, cut)

而去掉递归恶化处理之后的introsort_loop为：

template <class _RandomAccessIter, class _Tp, class _Size, class _Compare>

void __introsort_loop(_RandomAccessIter __first,
                      _RandomAccessIter __last, _Tp*,
                      _Size __depth_limit, _Compare __comp)
{
  while (__last - __first > __stl_threshold) {
    // 去掉了递归恶化处理
    _RandomAccessIter __cut =
      __unguarded_partition(__first, __last,
                            _Tp(__median(*__first,
                                         *(__first + (__last - __first)/2),
                                         *(__last - 1), __comp)),
       __comp); // 获取pivot
    __introsort_loop(__cut, __last, (_Tp*) 0, __depth_limit, __comp); //执行右侧
    __last = __cut; // 执行左侧
  }
}

pivot的获取

此处用的__median函数来实现。这个函数基本就是选择a、b和c中间的一个
template <class _Tp>

inline const _Tp& __median(const _Tp& __a, const _Tp& __b, const _Tp& __c) {
  __STL_REQUIRES(_Tp, _LessThanComparable);
  if (__a < __b)
    if (__b < __c)
      return __b;
    else if (__a < __c)
      return __c;
    else
      return __a;
  else if (__a < __c)
    return __a;
  else if (__b < __c)
    return __c;
  else
    return __b;
}

__unguarded_partition

template <class _RandomAccessIter, class _Tp>

_RandomAccessIter __unguarded_partition(_RandomAccessIter __first, 
                                        _RandomAccessIter __last, 
                                        _Tp __pivot) 
{
  while (true) {
    while (*__first < __pivot)// 1
      ++__first; 
    --__last; // 2
    while (__pivot < *__last) // 3
      --__last;
    if (!(__first < __last)) // 4
      return __first;
    iter_swap(__first, __last); // 5
    ++__first; // 6
  }
}    

快排的核心，是对pivot进行分割。小于pivot的在左边，大于pivot的在右边。STL中使用__unguarded_partition进行该操作。

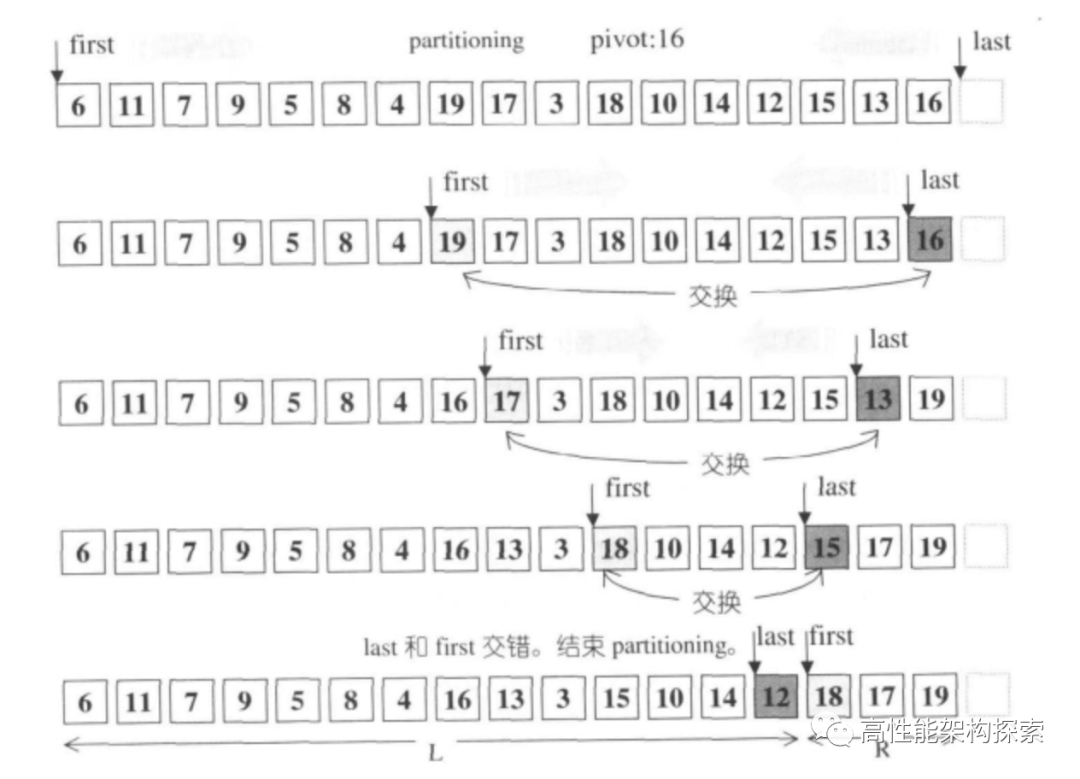
1和6都是将 first 迭代器后移，指向第一个不小于pivot的元素。2和3都是将 last 迭代器前移，指向第一个不大于pivot的元素。在4处的判断，若第一个不小于主元的元素不先序于第一个不大于pivot的元素，则说明分割已经完毕，返回第一个不小于pivot的元素的位置，即 first 的当前值；否则，在5处交换 first 和 last 指向元素的值。参考《STL 源码剖析》的图示：

分割图示例一

分割图示例二

__introsort_loop总结

1、在__introsort_loop函数中，首先会判断数据量大小，即如果last - first <= 16，则退出该函数。否则

2、判断__depth_limit是否为0。当该参数为 0 时，意味着递归深度已经很深，很可能快排掉入了陷阱，因此调用堆排，并退出递归。

3、每执行一次循环，depth_limit递减一次。

4、通过__unguarded_partition进行快排核心操作。

5、执行有半部分

6、通过__last = __cut;操作，下一步对左半部分进行排序。

__final_insertion_sort

代码实现如下：

template <class _RandomAccessIter, class _Compare>

void __final_insertion_sort(_RandomAccessIter __first, 
                            _RandomAccessIter __last, _Compare __comp) {
  if (__last - __first > __stl_threshold) {
    __insertion_sort(__first, __first + __stl_threshold, __comp);
    __unguarded_insertion_sort(__first + __stl_threshold, __last, __comp);
  }
  else
    __insertion_sort(__first, __last, __comp);
}

该函数内有一个if分支，判定数据量是否大于阈值16，

1、如果大于16，则对数据的第一个到第十六个进行插入排序，剩下的部分，进行__unguarded_insertion_sort排序

2、如果小于16，则直接进行插入排序

__linear_insert

template <class _RandomAccessIter, class _Tp, class _Compare>
inline void __linear_insert(_RandomAccessIter __first, 
                            _RandomAccessIter __last, _Tp*, _Compare __comp) {
  _Tp __val = *__last;
  if (__comp(__val, *__first)) {
    copy_backward(__first, __last, __last + 1);
    *__first = __val;
  }
  else
    __unguarded_linear_insert(__last, __val, __comp);
}

该函数的目的是将 last 所指向的元素插入到正确位置，这里蕴含的前提假设是[first, last) 区间的元素是已经排好序的。在这一假设下，若 *last < *first，则毫无疑问，last 指向的元素应当插入在上述区间的最前面，因此有 std::copy_backward；若不满足条件判断，则在 [first, last) 之间必然存在不大于 value 的元素（比如至少 *first 是这样），因此可以调用 __unguarded_linear_insert 来解决问题，而不必担心在 __unguarded_linear_insert 中 next 迭代器向左越界。对于 *last < *first 的情况，__linear_insert 将 last - first - 1 次比较和交换操作变成了一次 std::copy_backward 操作，相当于节省了 last - first - 1 次比较操作。

__insertion_sort

template <class _RandomAccessIter, class _Compare>

void __insertion_sort(_RandomAccessIter __first,
                      _RandomAccessIter __last, _Compare __comp) {
  if (__first == __last) return;
  for (_RandomAccessIter __i = __first + 1; __i != __last; ++__i)
    __linear_insert(__first, __i, __VALUE_TYPE(__first), __comp);
}

在该函数中 ，通过循环调用__linear_insert，从first之后的第一个元素开始，将该元素插入正确的位置。而这就是标准的插入排序了，此处不再赘述。

__unguarded_insertion_sort

template <class _RandomAccessIter, class _Tp, class _Compare>
void __unguarded_insertion_sort_aux(_RandomAccessIter __first, 
                                    _RandomAccessIter __last,
                                    _Tp*, _Compare __comp) {
  for (_RandomAccessIter __i = __first; __i != __last; ++__i)
    __unguarded_linear_insert(__i, _Tp(*__i), __comp);
}


template <class _RandomAccessIter, class _Compare>
inline void __unguarded_insertion_sort(_RandomAccessIter __first, 
                                       _RandomAccessIter __last,
                                       _Compare __comp) {
  __unguarded_insertion_sort_aux(__first, __last, __VALUE_TYPE(__first),
                                 __comp);
}

__unguarded_insertion_sort 没有边界检查，因此它一定比 __insertion_sort 要快。但由于 __unguarded_insertion_sort_aux 会从 first 开始调用 __unguarded_linear_insert；因此使用 __unguarded_insertion_sort 的条件比 __unguarded_linear_insert 更加严格。它必须保证以下假设成立：在 first 左边的有效位置上，存在不大于 [first, last) 中所有元素的元素。

__unguarded_linear_insert

template <class _RandomAccessIter, class _Tp>
void __unguarded_linear_insert(_RandomAccessIter __last, _Tp __val) {
  _RandomAccessIter __next = __last;
  --__next;
  while (__val < *__next) {
    *__last = *__next;
    __last = __next;
    --__next;
  }
  *__last = __val;
}

这里仅仅挨个判断是否需要调换，找到位置之后就将其插入到适当位置。

它根本无需输入左边界，而只需输入右边界迭代器和带插入元素的值即可；这也意味着，__unguarded_linear_insert 不是完整的插入排序的实现。

显然，这种情况下，为了保证函数执行的正确性，函数必然有额外的前提假设。此处假设应当是：while 循环会在 next 迭代器向左越界之前停止；这也就是说，在 [first, last) 之间必然存在不大于 value 的元素。因此，为防止越界，在调用该函数模板之前，我们必须要保证这一假设成立。

__final_insertion_sort总结

1、数据量与__stl_threshold对比。

2、如果大于__stl_threshold，则对前16个进行插入排序。对后16个进行__unguarded_insertion_sort 排序

3、如果小于__stl_threshold，则直接进行插入排序

写在最后

一直都对std::sort的函数实现很好奇。工作中经常用到，之前也只是大概了解到用到了快排 插入等，但是没有想到其为了效率，做了如此多的工作。c++的道路，漫长且困难。