IEEE 754 双精度浮点数

2878次阅读  |  发布于3年以前

double-precision floating-point format 双精度浮点格式

双精度浮点格式，也称 FP64 或 float64，是计算机的一种数字格式。通常在内存中占 64 位，且使用浮动的小数点来表示较宽的数值范围。

在 IEEE 754-2008 标准中，64 位 base-2 格式被正式称为 binary64。它在 IEEE 754-1985 中被称为 double。

IEEE 754 也指定了其它浮点格式，包括 32 位 base-2 单精度和最近的 base-10 表示。

最早提供单/双精度浮点数据类型的编程语言之一是 Fortran。在广泛采用 IEEE 754-1985 之前，浮点数据类型的表示和属性取决于计算机制造商、计算机模型以及编程语言的实现者（比如 GW-BASIC 的双精度数据类型是 64 位 MBF 浮点格式）。

双精度二进制浮点数

IEEE 754 double-precision binary floating-point format: binary64 IEEE 754 双精度二进制浮点格式: binary64

双精度二进制浮点数，即 binary64，通常简称为 double。IEEE 754 标准规定 binary64 有：

“有效数”也称尾数或系数，它是浮点表示或科学记数法中的一部分，由有效数字组成。

64 bits = 1 + 11 + 52

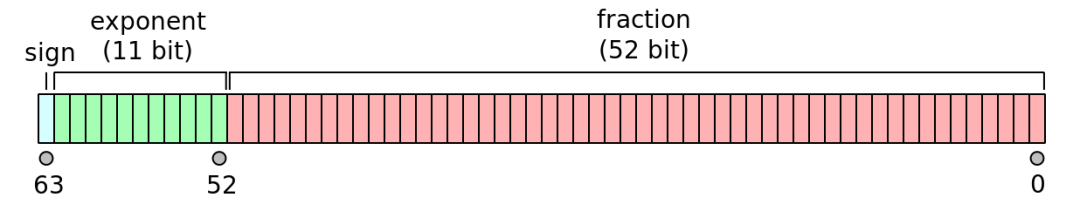
其中，符号位决定了数字本身的符号。指数是偏差指数，需要减去差值 1023（详见下一节“偏差指数”）。有效数精度是52位显式存储加1个隐藏位（值固定是1），所以能表示 53 位。

偏差指数

在 IEEE 754 浮点数中，指数在工程意义上是有偏差的，也称偏差指数。

之所以有偏差，是因为指数必须是“有符号”的值才能同时表示微小值和巨大值，但二进制补码（通常表示有符号值）会让比较变得更加困难。为了解决这个问题，指数被存储为适合比较的“无符号值”，然后在解释的时候“减去偏差”就转成有符号范围内的指数了。

偏差的值是 2k-1-1，其中 k 是指数的位数。比如：

双精度浮点数的指数字段是 11 位无符号整数，值从 0 到 2047。由于全 0 和全 1 的指数值是为特殊数字保留的，所以可用的指数值是从 1 到 2046。减去指数偏差值 1023，就能得到指数的实际范围，即从 -1022 到 +1023。

1 - 1023 = -1022 2046 - 1023 = +1023

科学记数法

科学记数法是一种记数方法。比如：

十进制表示法 科学记数法
0.00000000751 7.51*10-9
0.00001 1*10-5
0.2 2*10-1
2 2*100
4321.768 4.321768*103
−64000 -6.4*104
8100000000 8.1*109

在科学记数法里，基数可以是 2, 10, 16*

上表是基数为 10 的科学记数法

当数字过大或者过小的时候，用十进制表示通常要写一长串数字，此时用科学记数法就比较方便了。科学家、数学家和工程师们通常使用十进制的科学记数法，部分原因是它可以简化某些算术运算。

在十进制的科学记数法里，非零数字的写法是：a * 10n，其中 1≤|a|<10，n 是整数。

在计算机存储中，更常见的是二进制的科学记数法，即 a * 2n，其中 a 是由 0 和 1 组成的二进制表示，n 是整数。比如：

十进制数字 二进制表示 二进制科学记数法
1 1 1*20
2 10 1.0*21
3 11 1.1*21
4 100 1.00*22
5 101 1.01*22
6 110 1.10*22
8 1000 1.000*23
9 1001 1.001*23
11 1011 1.011*23
15 1111 1.111*23

binary64 的存储

综上，我们知道了给定的 64 位双精度数据在内存中的格式及其含义。

64 bits = 1 + 11 + 52

那么，它对应的真实数值就是：

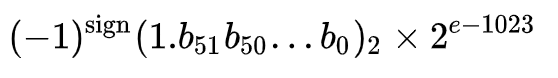
符号位，值为 0 或 1 有效数是小数，故是在后面补 0 指数是无符号数，故是在前面补 0

或者

因为有效数的首位一定是 1，所以在存储的时候就被省略了，只保存后面的数字部分，这样就可以节省一位有效数字位了。正因如此，52 位的有效数字位能表示 53 位。

接下来，和大家一起感受下，十进制数值是如何以“双精度二进制浮点数”的格式存储在内存中的。

举几个栗子

要想在计算机中存储十进制数字，需要：

1 . 将十进制转为二进制

2 . 将二进制写成科学记数法的形式

3 . 调整指数。根据前面“偏差指数”小节的介绍，真实存储的指数应该再加上 (211-1-1)(10) 即 1023(10)

4 . 标准化有效数，即省略最高位的 1

5 . 指数和有效数不足位的用 0 补齐，再依据符号(1位) + 指数(11位) + 有效数(52位)的格式，将值依次填充在 64-bit 中即可

以 168 为例

第一步，将十进制转为二进制。168(10) = 1010 1000(2)，逻辑如下：

除 2 取余数，直到商为 0 为止

第二步，将二进制写成科学记数法的形式。1010 1000(2) = 1.0101 000(2) * 27 = 1.0101(2) * 27。此时：

第三步，调整指数。7 + (211-1-1) = 7 + 1023 = 1030。转成二进制就是 1030(10) = 100 0000 0110(2)，逻辑如下：

除 2 取余数，直到商为 0 为止

第四步，标准化有效数。1.0101 省略首位的 1 之后就变成了 0101。

第五步，用 0 补齐指数（11位）和有效数（52位），最后再依次拼接即可。

168 的 64 bits IEEE 754 格式

以 0.125 为例

第一步，将十进制转为二进制。0.125(10) = 0.001(2)，逻辑如下：

乘 2 取整数，直到小数部分为 0

第二步，将二进制写成科学记数法的形式。0.001(2) = 1(2) * 2-3。此时：

第三步，调整指数。-3 + (211-1-1) = -3 + 1023 = 1020。转成二进制就是 1020(10) = 11 1111 1100(2)，逻辑如下：

除 2 取余数，直到商为 0 为止

第四步，标准化有效数。1 省略首位的 1 之后就变成了 0。

第五步，用 0 补齐指数（11 位）和有效数（52 位），最后再依次拼接即可。

0.125 的 64 bits IEEE 754 格式

以 0.1 为例

第一步，将十进制转为二进制。0.1(10) = 0.0 0011 0011 0011 ...(2)，逻辑如下：

乘 2 取整数，直到小数部分为 0

此时，我们发现出现了循环（0011），用小数部分乘以 2 以后永远也不可能得到小数部分是 0 的情况。这个时候，就要进行四舍五入了。由于二进制只有 0 和 1，所以就 0 舍 1 入。这个就是计算机在存储小数时会出现误差的原因所在了，但因为保留的位数很多，精度较高，所以在大部分情况下误差可以忽略不计。

第二步，将二进制写成科学记数法的形式。0.0 0011 0011 0011 ...(2) = 1.1001 1001 1001 ...(2) * 2-4。此时：

第三步，调整指数。-4 + (211-1-1) = -4 + 1023 = 1019。转成二进制就是 1019(10) = 11 1111 1011(2)，逻辑如下：

除 2 取余数，直到商为 0 为止

第四步，标准化有效数。1.1001 1001 1001 ... 省略首位的 1 之后就变成了 1001 1001 1001 ...。

第五步，用 0 补齐指数（11 位）和有效数（52 位），最后再依次拼接即可。

0.1 的 64 bits IEEE 754 格式

结束语

本文重点介绍了双精度二进制浮点数（即 binary64，也称 double）的格式及三个字段的含义。

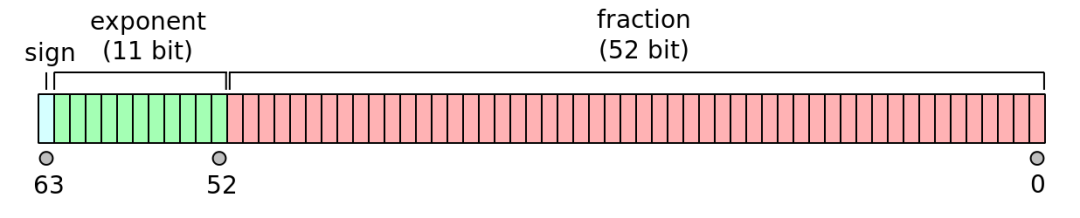
需要特别注意的是，当它在存储小数的时候，可能会有精度损失（比如上方 0.1 的例子）。

只要是符合 IEEE 754 标准的（如 Fortran 里的 real64 类型、Java / C# / C / C++ 里的 double 类型、JavaScript 里的 Number 类型等），在存储小数的时候都有可能出现误差。这个在对精度要求比较高的场景下，是不能忽略的。常规的替代方案就是先将小数转成整数（大数）进行存储和运算，最后显示的时候再恢复成小数形式。

主要参考

Copyright© 2013-2020

All Rights Reserved 京ICP备2023019179号-8