性能分析不一定得用 Profiler，复杂度分析也行

352次阅读  |  发布于3年以前

如果提到性能分析，你会想到什么呢？

可以做耗时分析、内存占用的的分析。可以用 chrome devtools 的 Profiler，包括 performance 和 memory，分别拿到耗时和内存占用的数据，而且还可以用火焰图做可视化分析。

比如 performance，你可以看到每个函数的耗时，通过简单的加减法，就能算出是哪个函数耗时多，然后去优化。

而且，你可以勾选 memory，显示堆内存的变化，可以知道是哪个函数导致的内存增多，然后去优化。

当然，你也可以单独分析 memory 的 timeline，录制一段时间的内存占用情况，然后看这时候的内存中有哪些对象，这样比只知道大小更精确一些。

总之，我们可以通过调试工具的 Profiler 来看到内存和耗时，然后关联到具体的函数，之后着手去优化。

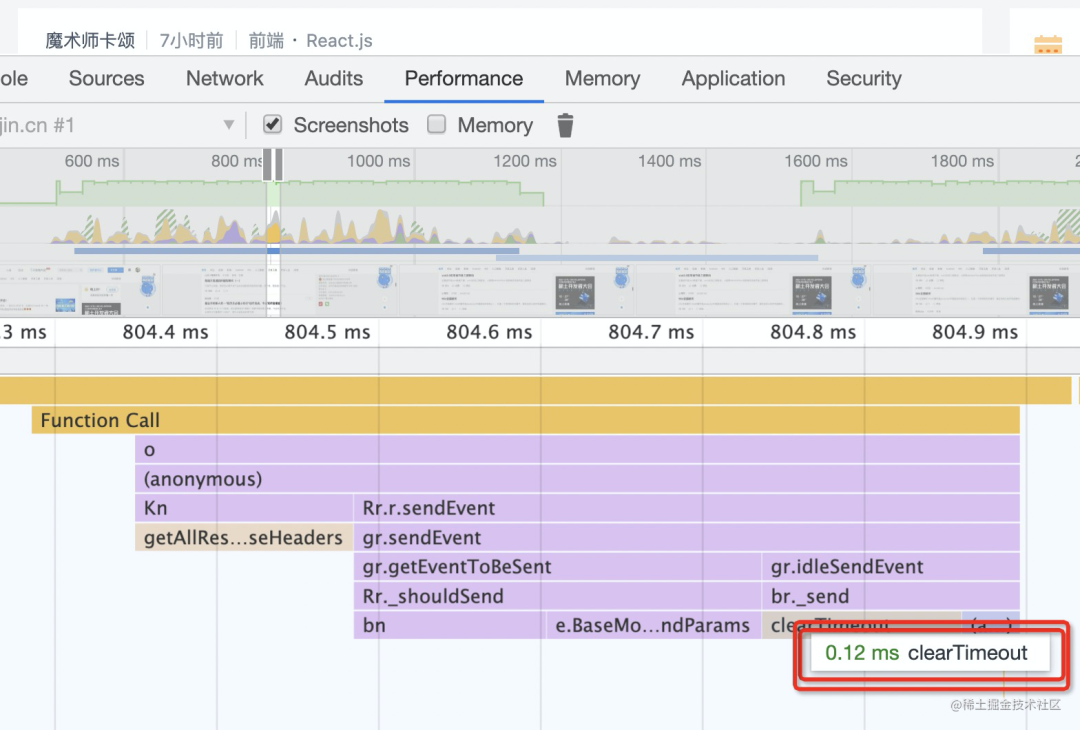
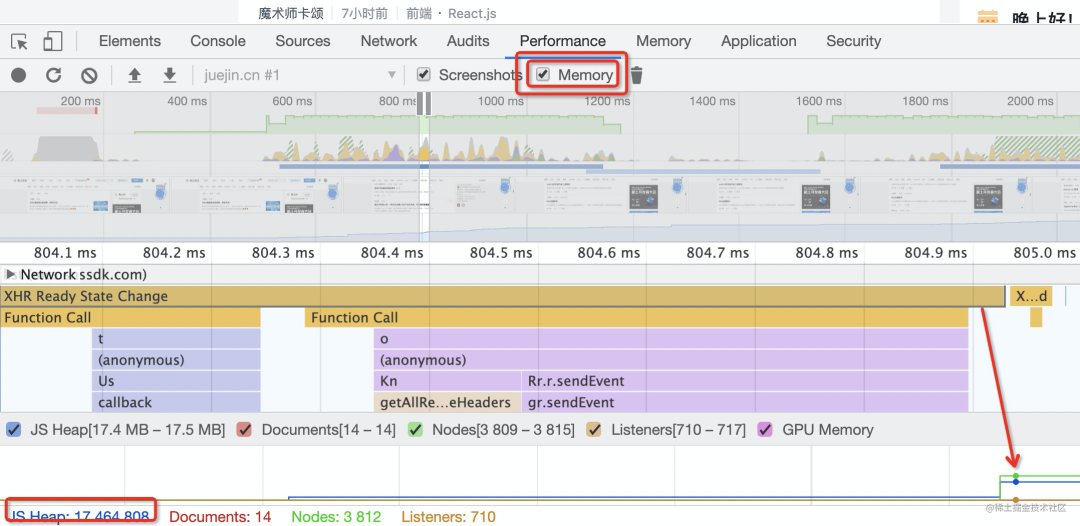
但是，这些都是代码跑起来才能统计的，而且与机器、不同的输入数据等强相关。

如果换一台机器，数据就是另一个样子了。这也是为啥测试的时候要用各种机器测一遍。

那如果想代码不运行就能估算出具体时间和内存占用大小，有什么思路么？

这就是复杂度分析技术做的事情了。

这篇文章我们来学下复杂度分析是如何估算时间的。

1. 复杂度分析的几个基础

1.1 什么是 1，什么是 n

如果有这样一行代码：

const name = 'guang';

耗时多少，内存多少？

你可能说得跑跑看，可能耗时 1ms，内存 4 bytes，也可能耗时 2ms，内存 8bytes 等等，不同的机器和运行环境都会有不同。

但我们都把它作为 1 ，这个 1 不是 ms，不是 byte，只是说是一个耗时/内存占用的基本单元，也就是复杂度是 1。

那这样的代码呢？

function calc(n) {
    for(let i = 0; i < n; i ++) {
        //...
    }
}

具体的数值随着 n 的增大而增大，复杂度是 n。

我们分析复杂度的时候，不会分析具体的耗时和内存占用，而是以语句作为复杂度的单元，也就是 1，随着输入的数据规模 n 而变化的复杂度作为 n。

1.2 渐进的时候，常数可省略

我们知道了 1 和 n，就可以计算这些复杂度了：


function func(n) {
    const a = 1;
    const b = 2;

    for (let i = 0; i < n; i ++) {
       //...
    }
}

这里面有两条语句，复杂度是 1 + 1，一个循环 n 次的语句，复杂度是 n，所以总复杂度是 2 + n。

复杂度(func) = 2 + n

当这个 n 逐渐变大的时候，比如 n 变成了 10000000，那这个 2 就可以忽略不计了。

也就是

复杂度(func) = O(n)

这个 O 是渐进复杂度的意思，也就是渐渐的增大的时候的复杂度。

有的同学说，这里是 2，所以可以省略，如果这里有 100000 条呢？是不是就不能省略了？

其实也会省略，因为不管多大，它的复杂度总是一个常数，是固定的，不会变化，所以不用分析进去，估算出的耗时或者内存占用加上它那固定的部分就可以了。而变化的部分才需要分析。

当我们计算渐进复杂度 O 的时候，常数会省略掉，因为它是固定的，不会变，而我们只分析变化的部分，也就是与 n 有关的部分。

1.3 多个变化的输入数据规模时，都要计算

上面只是有一个输入数据，规模是 n 的时候，复杂度与 n 有关。

如果有两个输入数据，规模分别为 m 和 n 的时候，那都要计算上，不能省略，因为都是变化的。

也就是 O(m + n)、 O(m * n) 这种。

2. 一些常见的时间复杂度

我们明白了什么是 1，什么是 n，什么时候要同时计算 m 和 n，什么是渐进复杂度，为什么常数可以省略之后，就可以看一些实际的复杂度的例子了。

其实复杂度也就这么几种：O(n)、O(n^2)、O(logn)、O(2^n)、O(n!)

O(n)

function func(n) {
    const a = 1;
    for(let i = 0; i < n; i ++) {
        //...
    }

}

这种就是 O(n)，我们上面分析过。常数复杂度省略掉。

O(n^2) O(n^3)

function func(n) {
    for(let i = 0; i < n; i ++) {
        for(let j = 0; j < n; j ++) {
            //...
        }
    }
}

这种就是 O(n^2)，同理，O(n^3)、O（n^4）等也一个意思，就是嵌套的时候，复杂度相乘。

O(logn)


let n = 100; 
let i = 1; 
while(i < n){ 
    i = i * 2 
}

这段代码要计算多少次，要看 i 乘以几次 2 才大于 100，也就是 log2n

那同理，也有 log3n，log4n 等复杂度，当渐进复杂度的时候，常数是不用计算的，所以都是 O(logn)

o(2^n) o(3^n)


const fibnacci = function (n) { 
    if (n <= 1) return n; 
    return fibnacci(n - 1) + fibnacci(n - 2);
};

斐波那契数列我们都知道，可以用上面的递归来算。

这样算的话，n 每加 1，就多递归调用了 2 次 fibnacci 函数，也就是复杂度乘以 2 了，所以复杂度是 O(2^n)。

同理，如果 n 每加一，多递归执行 3 次，那就是 O(3^n) 的复杂度。

也就是说，n 每加一，多递归 a 次，那复杂度就是 O(a^n)。

O(n!)

function func(n) { 
    for(let i=0; i<n; i++) { 
        func(n-1); 
    }
}

上一条我们知道了，n 每加 1，多递归常数次，是指数型，那如果如果当 n 每加 1，多递归 n 次，这种就是复杂度 o(n!) 了。

为什么不是 O(n^n) 呢？因为 n 是变化的啊，所以是 O(n!)。

这基本是全部的时间复杂度情况了。当然，这里只是讨论了 n 一个纬度，再多一个纬度 m 的话，也是一样。

下面我们来区分一下这些时间复杂度的优劣。

3. 时间复杂度的优劣对比

我们学习了大 O 的渐进时间复杂度表示法，就是为了估算 n 与具体执行时间的关系。

上面分析出的几种时间复杂度，它们与具体执行时间的关系是什么样的呢？可以画出变化函数来分析。

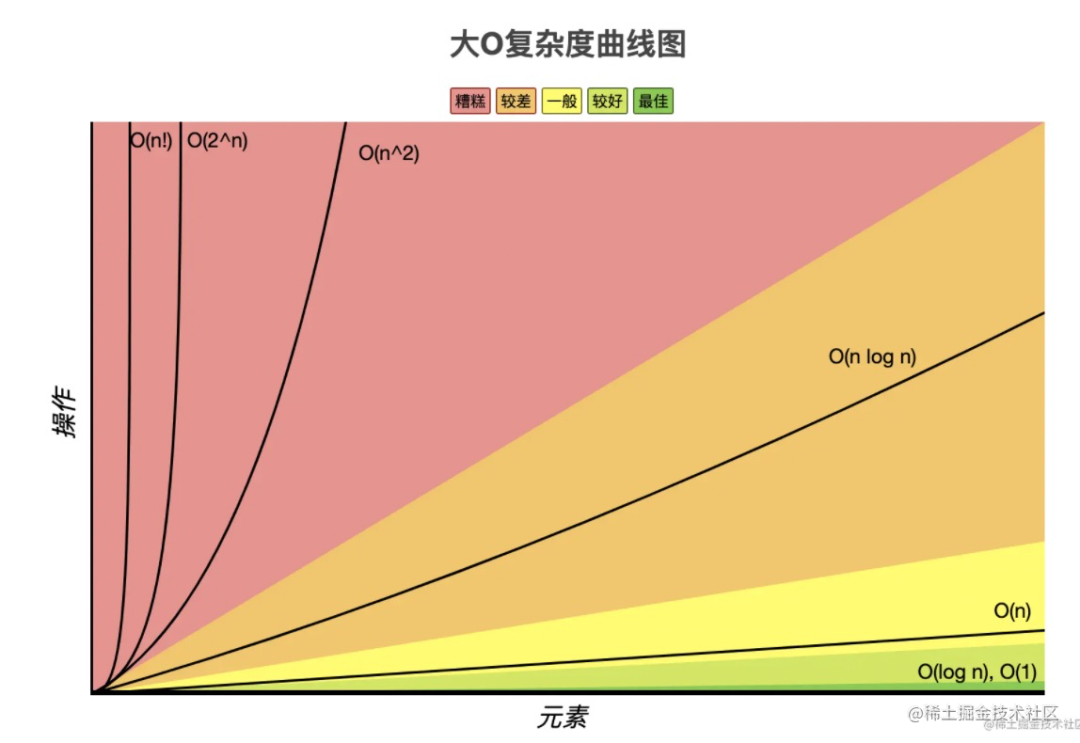
可以看到，随着 n 的增大， O(n!) 和 O(2^n) 是耗时增加最快的，也就是说，这样的代码，n一旦大了，立马会卡死，不用跑我们就能分析出来。

那什么样是的不容易卡死的呢？O(n)、O(nlogn)、o(logn)这种，随着数据规模的增大，耗时也不会增大很多。

所以我们说:

根据这个结论，我们就可以评判一些代码写法的好坏，也就是算法的优劣了。

需要真实去跑代码么？不需要。

4. 空间复杂度

空间复杂度也就是堆栈内存的分配与输入数据规模 n 的关系。

这里不包括全局变量，为什么呢？全局变量不会动态变啊，就相当于常数，可以省略，只分析变化的堆栈内存的复杂度就好了。

空间复杂度的分析方式和时间复杂度是类似的，只是不是把每一条语句作为 1，而是只把会分配内存的语句作为 1 来分析。

比如下面这段代码的空间复杂度就是 O(n)。


function func(n) {
    let arr = [];
    for (let i = 0; i < n; i++) {
        arr.push(i);
    }
}

总结

分析性能一般通过运行时的 Profiler 来收集数据，然后分析耗时和内存占用，比如 chrome devtoos 的 performance 和 memory 工具。

但是其实不用运行代码，我们也可以通过复杂度来估算出来：

我们把一条语句作为复杂度是 1，而随着输入数据规模 n 变化的为复杂度 n。

我们估算是为了分析出耗时/内存占用随着数据规模 n 的一个变化关系，所以会用 O(n) 来表达这种变化关系，叫做渐进时间复杂度。

求渐进时间复杂度时，常数可以省略，因为它们是固定不变的，而我们只需要分析变化的部分。

复杂度基本就 O(n) O(logn) O(n^2) O(2^n) O(n!) 这几种。

其中要注意的是 O(2^n) 就是当 n 每加一，多递归 2 次，而如果 n 每加 1，多递归 n 次，那么就是 O(n!) 的复杂度。

O(2^n) 和 O(n!) 的复杂度都是随着 n 增加，复杂度急剧增加的，也就是耗时/内存占用会急剧增加，这样的代码很容易卡死，所以是不好的。

而 O(logn) O(n) 都是随着 n 增加，复杂度增加很少的。也就意味了耗时更少，内存占用更少。这样的算法当然也就更好了。

所以我们就是通过复杂度来评价算法好坏的，它就代表了耗时/内存占用，但不是直接表示的，而是抽象的表示。

如果说想得到不同机器、环境下的具体耗时/内存占用，那么就用 Profiler 在运行时收集数据，然后做分析和可视化，否则，其实通过复杂度就能够抽象的估算出来大概的耗时和内存占用。

性能分析不一定得用 Profiler，复杂度分析也行，它能评价一个代码写法（算法）的好坏，进而估算出性能。

- EOF -

Copyright© 2013-2020

All Rights Reserved 京ICP备2023019179号-8