快速了解一条曲线是如何从 0 到 1 诞生的

引言

在图可视化领域有着大量和曲线相关的场景，然而想要得到一条合适的曲线却并不容易。笔者最近在使用 AntV G6 的时候，就遇到了这样的问题。形状扁平，箭头方向和连线趋势不一致，连线起点和终点被隐藏等等，好看的曲线总是相似的，而丑陋的曲线却各有各的问题。如何得到一条好看的曲线呢 ？来一探究竟吧。

问题

AntV G6 自带了 cubic-vertical 连线，即竖直方向上的三阶贝塞尔曲线，但是这种连线不支持传入控制点。连线自身较不美观，且无法处理一些极端情况，如下图所示。图 2 中曲线过于扁平，连线趋势和末端箭头的方向偏离角度太大；图 3 中，箭头和连线起始点完全被遮盖。

图1

图 1

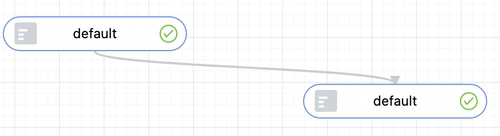
图 2

图 2

图 3

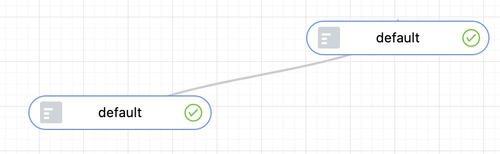
图 3

其他图编辑产品的连线

他山之石，可以攻玉。为了提升用户的连线体验，我们横向比较了其他图编辑产品的连线方案。共找到 4 个较为相似的知名产品。其中 Draw.io 和 Processon 是比较偏重于图编辑场景的，二者都支持贝塞尔曲线，都支持通过拖拽控制点的方式来让用户改变曲线形状。但这种交互方式相当于把优化曲线的任务交给了用户，和我们的目标不同。另外 DataV 的蓝图编辑器和 AntV X6 的示例都是轻量级的图编辑场景，二者都是通过优化调整三次贝塞尔曲线来获取更好的连接效果。下面详细阐述各种连线方案。

Draw.io

draw.io 十分偏重图编辑，支持三阶贝塞尔曲线，高阶贝塞尔曲线，用户可以通过拖拽控制点生成任意复杂，任意形状的曲线。如下图所示，draw.io 支持在拖拽曲线的时候，增加或减少控制点，可以调整锚点的连接位置，调整末端箭头的方向。

图 4

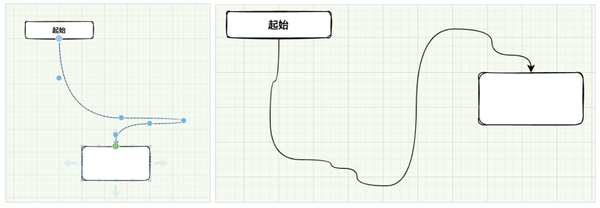
图 4

Draw.io 的优势在于：

1. 支持动态增删控制点，用户几乎可以绘制出任意形状的曲线。
2. 拖动曲线或控制点时，锚点连接位置和末端的箭头方向可以自适应调整，以获得更好的效果。如上图所示。

其缺点在于：

1. 交互较为复杂，上手难度高。
2. 实现复杂，动态增删控制点逻辑复杂。

ProcessOn

Processon 同样偏重图编辑，但仅支持三阶贝塞尔曲线，用户可以通过拖拽控制点调整曲线形状，拖拽控制点过程中箭头方向会自动调整。且 Processon 的控制点位于曲线外，符合贝塞尔曲线的原始定义。此外，控制点和曲线的首尾两点之间有辅助线，便于用户感知控制点对于曲线形状的作用方式。

图 5

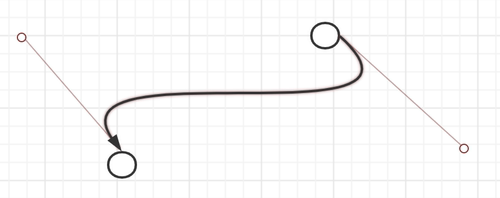
图 5

Processon 的优势在于：

1. 拖动控制点的过程中，末端箭头的方向会自动调整。
2. 控制点的交互较为简单，且有辅助线帮助用户理解。

其缺点在于：

1. 拖拽曲线后，再拖拽节点，曲线形状发生较大改变。
2. 与 Draw.io 一样，将曲线形状优化的任务交给了用户。

DataV 的蓝图编辑器

DataV 的蓝图编辑器仅支持三阶贝塞尔曲线，不支持拖拽控制点，但其连线效果很好，连线末尾的箭头在拖动节点的过程中也会自适应调整形状。

另外，蓝图编辑器限制了锚点是输出还是输入，如指定节点左侧的锚点仅支持输入，节点右侧的锚点仅支持输出。这样设置，能够减少连线所需要处理的特殊情况。

图 6

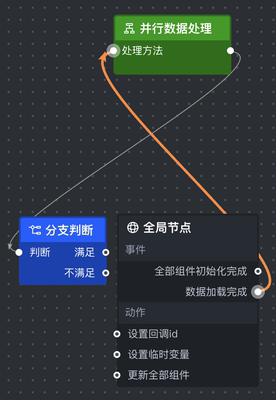
图 6

DataV 蓝图编辑器的优点在于：

1. 连线为简单的贝塞尔三阶曲线，仅通过调整控制点参数来适应节点拖动所形成的形状。
2. 节点拖动过程中，连线变化流畅。

其缺点在于：

1. 末端箭头的形状和曲线并不是完全贴合，如上图中橙色箭头所示。

AntV X6

AntV X6 与蓝图编辑器的效果相似，但实现方式不同。该示例同样根据锚点相对于节点的位置限制锚点是输入还是输出。X6 示例通过在贝塞尔曲线的两端添加两段直线来获取更好的连线效果，如下图所示。

图 7

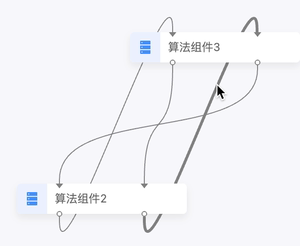
图 7

X6 的实现方式的优点在于：

1. 实现方式简单，仅在贝塞尔曲线两端添加直线，且贝塞尔曲线的参数为固定值。
2. 交互效果较为流畅。

其缺点在于：

1. 贝塞尔曲线参数固定，节点距离较近时，曲线过于 “弯曲”，如下图所示。

图 8

图 8

连线优化

本次曲线优化主要借鉴 AntV X6 的示例以及 DataV 蓝图编辑器的思路。

添加直线

设计思路

首先是借鉴 X6 的思路在连线两端添加直线，此方案的重点在于计算首尾两段直线的起点和终点。如下图所示，根据锚点相对于节点的方向，直线延伸的方向也有所不同。图中左侧开始节点的连接锚点位于节点的下方，所以开始端的直线要向下延伸，而终止端节点的连接锚点位于节点的上方，此时终止端的直线要向上延伸。而右图中开始节点的连接锚点位于节点的右侧，故开始端的连线要向右延伸。

图 9

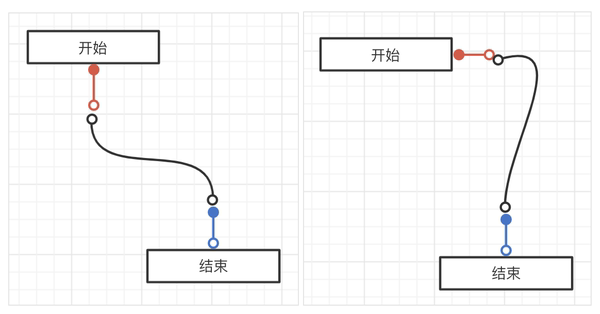
图 9

实现方案

为了验证我们思路的正确性，我们首先分析了 AntV X6 的曲线。

采集数据

连线形状	Path
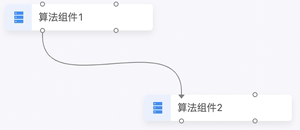	M -335 -185 L -335 -181 C -335 -101 -165 -194 -165 -114 L -165 -110
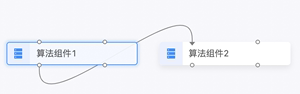	M -375 -75 L -375 -71 C -375 9 -165 -194 -165 -114 L -165 -110
	M -255 -95 L -255 -91 C -255 -11 -175 -324 -175 -244 L -175 -240

反推规律

根据上表中 path 这一列的数据，可以看出 AntV X6 在贝塞尔曲线两端添加直线的方式为：MoveTo 起点，LineTo 贝塞尔曲线的起点，然后 Curve，三阶贝塞尔曲线，最后 lineTo 终点。以第三行为例，M -255 -95 即移动到（-255， -95）这个点，然后 L -255 -91 即从（-255， -95）这个点画一条直线到（-255， -91）。接着，C -255 -11 -175 -324 -175 -244 即以（-255， -11）为第一个控制点，以（-175 ，-324）为第二个控制点，以（-175， -244）为贝塞尔曲线的终点绘制贝塞尔曲线。最后 L -175 -240 即从 （-175， -244）到（-175， -240）绘制直线。总结一下，第一条命令和最后一条命令中的坐标分别为连线的起点和终点。两段连线都是在 y 方向偏离起（终）点 4个单位，而贝塞尔曲线的两个控制点的 y 坐标分别为起 (终) 点的 y 坐标 +（-）80，而两个控制点的 x 坐标分别与起点和终点的 x 坐标相同。

用公式表达就是 ：

startPoint, endPoint
M startPoint.x  startPoint.y
L startPoint.x   startPoint.y+4
C startPoint.x  startPoint.y+4+80   endPoint.x endPoint.y-4-80  endPoint.x endPoint.y-4
L endPoint.x endPoint.y

实际效果

根据锚点相对于节点的位置来自适应两端直线的延伸方向能够让连线末尾的箭头保持正确的方向，同时连线起始和末尾的直线也保证了连线的方向能够被用户准确感知。如下图所示，图中左侧为默认的 cubic-vertical 曲线，图中红色圈中的连线部分，要么是起点端无法显示锚点相对于节点的方向，要么是终点的箭头被隐藏，这两种情况都会严重影响用户对于连线走向的感知。而右图中的连线完全避免了这两个问题，且连线走向更为清晰，流畅，更符合用户的心理感知。

图 10

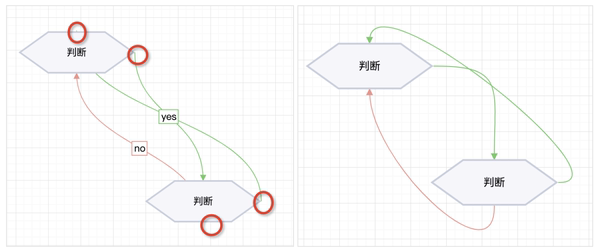
图 10

有待改进

然而，这种方案并非尽善尽美，单纯在贝塞尔曲线两端添加直线仍有两个问题需要解决。

1. 上述方案在计算 中段贝塞尔曲线的控制点时，使用了一个 Magic Numbe，常量 80, 导致当两个节点比较靠近时，曲线的形状有些奇怪，如下图中所示。

图 11

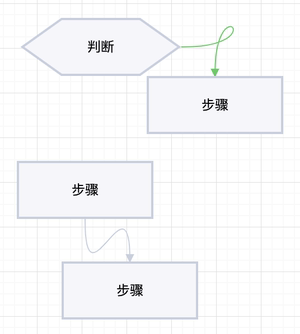
图 11

上述问题的核心在于，我们对于贝塞尔曲线的控制点和曲线形状之间的关系没有准确的理解，无法理解 Magic Number 背后的原理，对应的解法就是理解贝塞尔曲线的控制点，将 Magic Number 修改为 Func (startPoint, endPoint)。

2 . 上述方案在曲线连接的过程中没有感知用户的连接方向，导致箭头和曲线的形状在连线的过程和结果发生较大的变化。如下图所示，左侧为连接过程中曲线的形状和箭头方向，右侧为连接完成后的曲线形状和箭头方向。该问题的核心在于要在连线的过程中准确感知用户想要连接的方向，上述方案的做法是直接将连接方向等同于开始端连接锚点相对于节点的反方向。

图 12

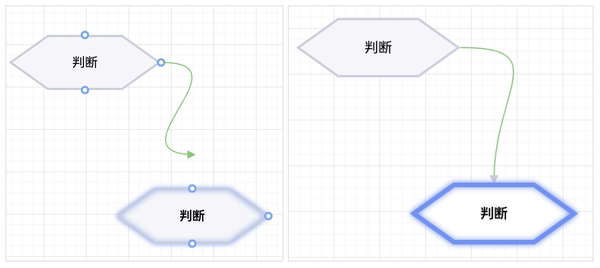
图 12

该问题的解决方案即：根据连接过程中连线末尾的坐标相对于 startPoint 的方位来确定连线的方向，改造效果如下图所示。

图 13

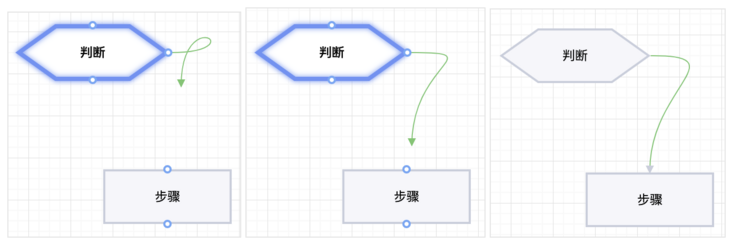
图 13

优化贝塞尔曲线的参数

除了借鉴 AntV X6 的连线方案，我们还希望借鉴 DataV 蓝图编辑器中的贝塞尔曲线。有了上述对 AntV X6 示例中连线的 “逆向工程” 之后，我们打算对 DataV 蓝图编辑器中的贝塞尔曲线也如法炮制。

实现方案

采集数据

曲线形状	Path	平移起点到坐标原点
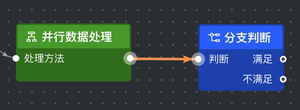	M 586.5 336 C 532.7496710549095 336 545.2503289450905 335.5 491.5 335.5	M 0 0 C -54 0 -41 0 -95 0
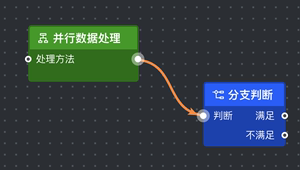	M 662.5 229 C 603.0729185103246 229 626.9270814896754 159.5 567.5 159.5	M 0 0 C -60 0 -36 -70 -96 -70
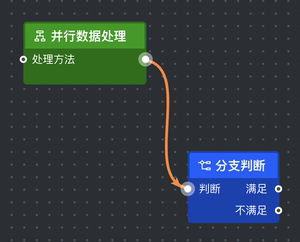	M 640.5 304 C 571.5182334289478 304 648.4817665710522 160.5 579.5 160.5	M 0 0 C -69 0 8 -144 -61 -144
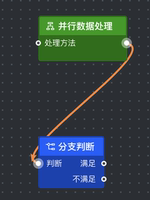	M 457.5 345 C 372.2029329439616 345 664.7970670560384 160.5 579.5 160.5	M 0 0 C - 85 0 207 -185 122 -185
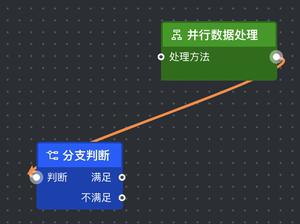	M 310.5 302 C 204.51346747613758 302 685.4865325238624 160.5 579.5 160.5	M 0 0 C -106 0 375 -142 269 -142
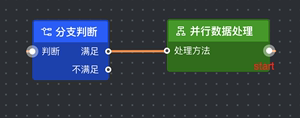	M 269.5 158 C 164.2498961794736 158 675.7501038205264 157.5 570.5 157.5	M 0 0 C -105 0 406 0 301 0
	M sx sy，C x1 y1 x2 y2 x3 y3，sy === y1，y2 === y3	M 0 0，C x1 y1 x2 y2 x3 y3，x1 + x2 === x3，y1 + y2 === y3

如上表所示， 我们采集了不同形状的贝塞尔曲线所对应的 Path，并试图直接找出其中的规律。第一列是曲线的形状，第二列是曲线对应的 Path，第三列是将曲线起点平移到坐标原点后的数据。

找出规律 ？

如上表最后一行所示，第二列仅仅找到了 y1 和 y2 坐标的规律，也就是控制点 1 和控制点 2 的 y 坐标的计算方式。而第三列所描述的等式中关于 x1 x2 的仅有一个 **二元一次方程 ，**此时是无法求出 x1 x2 的，我们至少还需要一个关于 x1 x2 的方程才能求出控制点的坐标。

摊手

但是如何找到另一个关于 x1、x2 的方程呢 ？先数形结合试一试，数无形则不直观。

图 14

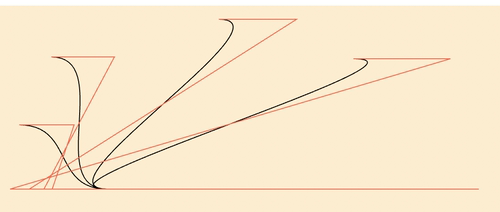
图 14

如上图所示，图中的黑色曲线对应上表中的四条数据，我们使用第三列的数据来绘制此图，希望通过将起点都集中到原点的方式来方便对比和发现规律。图中红色曲线的每个弯折点都是控制点。

我们可以从此图中得到以下几点知识：

1. 两个控制点相对于曲线的中点对称，也就是说，只要求出一个控制点就能得出另一个控制点。
2. 两个控制点在 x 方向上的距离要大于两个起点在 x 方向上的距离。
3. 不同形状曲线的控制点在 x 方向上到起点的距离不同，即控制点到起点在 x 方向上的距离不是常数。

得到这些结论之后，结合表中的规律，我们发现其实只要计算出单个控制点的坐标，就能得出另一个控制点的坐标了。而单个控制点的坐标中唯一要求的就是它的 x 坐标，也就是说，只要求出控制点在 x 方向上到起点的距离即可。

换个角度考虑，在绘制开始前，我们应该只知道一条曲线的起点和终点。也就是说控制点 x 坐标应该从是根据起点和终点计算出的，也就是 controlPoint.x = F (startPoint, endPoint)。但是，也有可能是controlPoint.x = F (startPoint.x, endPoint.x) 即控制点的 x 坐标仅仅由起点和终点的 x 坐标决定。

再拿点数据验证一下 ！

曲线形状	Path
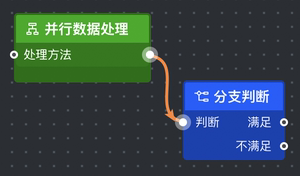	M 490.5 -146 C 439.9372150475671 -146 494.0627849524329 -213.5 443.5 -213.5
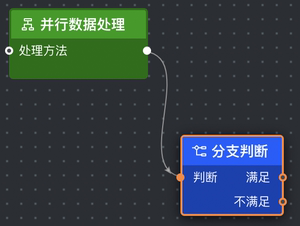	M 490.5 -89 C 427.23097348884403 -89 506.76902651115597 -213.5 443.5 -213.5

如上表所示，两条曲线形状的起点和终点的 x 坐标分别都相同，但是曲线的形状不同，控制点也不同 ！说明应当是 controlPoint.x = F (startPoint, endPoint)

但是如何求出 F 呢 ？

再次摊手

深挖一把

观察 controlPoint.x = F (startPoint, endPoint)，结合图 14，我们可以发现：坐标平移并不会改变曲线的形状，对计算控制点有意义的数据应该是起点和终点在 x 方向上和 y 方向上的距离。也就是说 controlPoint.x = F(startPoint, endPoint) 即是 ctrlDistanceX = F (distanceX, distanceY) 。

找 F 其实就是找规律。那可以用用概率统计里面的方法来拟合试试 ？也许规律足够简单，也可以先画图看看。但是第一步需要收集更多的数据。

1 . 更多的数据

为了更方便的采集更多的数据，我们直接在蓝图编辑器页面的控制台里来点代码。

const data = [];
const func = () => {
  const targetPath = document.querySelector('.butterflies-link');
  data.push(targetPath.getAttribute('d'));
}
const intervalId = setInterval(func, 1000);

然后去拖动节点，变化曲线的形状，最后先 clearInterval(intervalId), 然后在控制台里面输入 data，复制粘贴走获取的数据。

去重之后的数据如下所示 ：

 "M 524.5 72 C 402.67229108270203 72 527.327708917298 -275.5 405.5 -275.5",
        "M 587.5 -53 C 485.63630523692785 -53 507.36369476307215 -275.5 405.5 -275.5",
        "M 523.5 -85 C 437.4786592002655 -85 491.5213407997345 -275.5 405.5 -275.5",
        "M 407.5 173 C 265.3738851783404 173 547.6261148216596 -275.5 405.5 -275.5",
        "M 600.5 17 C 482.61468766056527 17 523.3853123394347 -275.5 405.5 -275.5",
        "M 600.5 17 C 481.18236106456914 17 939.8176389354309 -264.5 820.5 -264.5",
        "M 514.5 -1 C 383.54572507813253 -1 951.4542749218674 -264.5 820.5 -264.5",
        "M 355.5 -25 C 194.73655661844936 -25 981.2634433815506 -264.5 820.5 -264.5",
        "M 355.5 -25 C 203.2729443821868 -25 952.7270556178132 -227.5 800.5 -227.5",
        "M 355.5 -25 C 251.76642131972704 -25 751.2335786802729 -66.5 647.5 -66.5",
        "M 609.5 92 C 538.7521089502782 92 718.2478910497218 -66.5 647.5 -66.5",
        "M 609.5 92 C 538.5661738289713 92 717.4338261710287 -67.5 646.5 -67.5",
        "M 609.5 92 C 473.7472665837899 92 461.2527334162101 -221.5 325.5 -221.5",
        "M 309.5 124 C 193.03243021224662 124 441.9675697877534 -221.5 325.5 -221.5",
        "M 441.5 -199 C 381.95950872107915 -199 385.04049127892085 -221.5 325.5 -221.5",
        "M 441.5 -255 C 360.8441452051197 -255 428.1558547948803 -75.5 347.5 -75.5",
        "M 441.5 -255 C 301.5519298714161 -255 496.4480701285839 176.5 356.5 176.5",
        "M 242.5 -257 C 100.44023636915881 -257 498.5597636308412 176.5 356.5 176.5",
        "M 242.5 -257 C 93.61264522666846 -257 762.3873547733315 40.5 613.5 40.5",
        "M 649.5 -258 C 544.3342456633342 -258 718.6657543366658 40.5 613.5 40.5",
        "M 649.5 -258 C 560.515759520021 -258 712.484240479979 -23.5 623.5 -23.5",
        "M 649.5 -258 C 597.4897041137563 -258 614.5102958862437 -244.5 562.5 -244.5",
        "M 649.5 -258 C 597.4202440004424 -258 613.5797559995576 -250.5 561.5 -250.5",
        "M 641.5 -242 C 591.3874261965307 -242 611.6125738034693 -250.5 561.5 -250.5",
        "M 317.5 29 C 194.74486200215108 29 684.2551379978489 -250.5 561.5 -250.5",
        "M 600.5 -79 C 526.5303726988732 -79 635.4696273011268 -250.5 561.5 -250.5",
        "M 600.5 -79 C 525.5554160660041 -79 685.4445839339959 -258.5 610.5 -258.5",
        "M 600.5 -79 C 491.4951544207572 -79 1025.5048455792428 -75.5 916.5 -75.5",
        "M 570.5 140 C 438.59432977012517 140 1048.4056702298749 -75.5 916.5 -75.5",
        "M 568.5 176 C 465.1543925991474 176 800.8456074008526 -87.5 697.5 -87.5",
        "M 568.5 176 C 453.3999669506527 176 537.6000330493473 -131.5 422.5 -131.5",

2 . 处理数据

转换数据格式，计算出第一个控制点在 x 方向上到起点的距离，起点和终点在 x 方向上的距离，起点和终点在 y 方向上的距离。

 // 第一个控制点在 X 方向上到起点的距离
     [
        121.82770891729797, 101.86369476307215, 86.0213407997345,
        142.1261148216596, 117.88531233943473, 119.31763893543086,
        130.95427492186747, 160.76344338155064, 152.2270556178132,
        103.73357868027296, 70.74789104972183, 70.93382617102873,
        135.7527334162101, 116.46756978775338, 59.540491278920854,
        80.65585479488033, 139.94807012858388, 142.0597636308412,
        148.88735477333154, 105.16575433666583, 88.98424047997901,
        52.01029588624374, 52.07975599955762, 50.11257380346933,
        122.75513799784892, 73.96962730112682, 74.94458393399589,
        109.00484557924278, 131.90567022987483, 103.3456074008526,
        115.1000330493473,
      ]

            // 起点和终点在 X 方向上的距离
            [
        119, 182, 118, 2, 195, 220, 306, 465, 445, 292, 38, 37, 284, 16, 116,
        94, 85, 114, 371, 36, 26, 87, 88, 80, 244, 39, 10, 316, 346, 129, 146,
      ]

      // 起点和终点在 Y 方向上的距离
      [
        347.5, 222.5, 190.5, 448.5, 292.5, 281.5, 263.5, 239.5, 202.5, 41.5,
        158.5, 159.5, 313.5, 345.5, 22.5, 179.5, 431.5, 433.5, 297.5, 298.5,
        234.5, 13.5, 7.5, 8.5, 279.5, 171.5, 179.5, 3.5, 215.5, 263.5, 307.5,
      ]

3 . 尝试分析

直接看肯定看不出什么的，画个图试试。

图 15

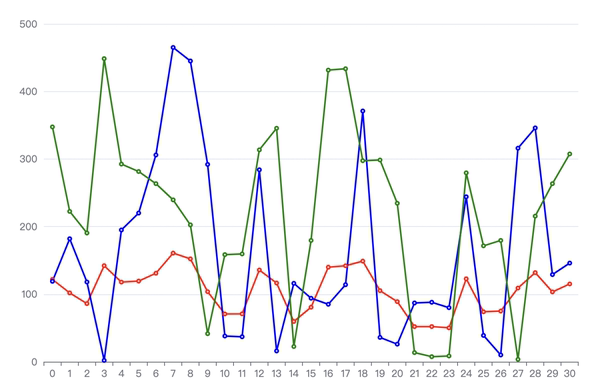
图 15

图中横坐标是不同的贝塞尔曲线的 id，纵坐标是距离，红色折线是第一个控制点在 x 方向上到起点的距离，蓝色折线是起点和终点在 x 方向上的距离，绿色折线则是起点和终点在 y 方向上的距离。

好像看不出什么趋势，排个序试一试。

图 16

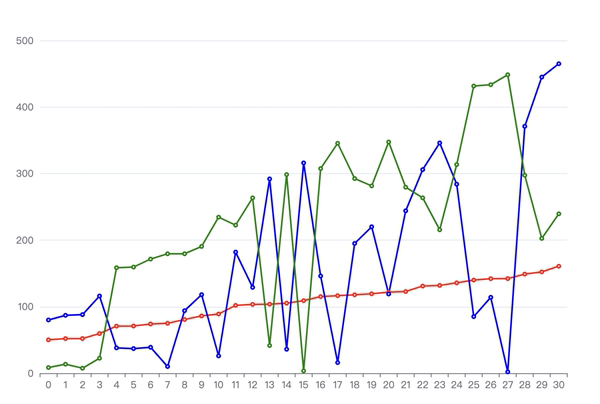
图 16

红色折线总是位于蓝色折线和绿色折线之间，类似于平均值的关系，应该是 z = ax + by 的形式。在这里，我尝试了 a = b = 0.5 | 0.4 ... 并观察不同的计算结果得出的折线与红色折线的贴合程度。如下图所示，图中黑色折现即 a = b = 0.5 时的计算结果，但是最优结果肯定不是试出来的 ...

图 17

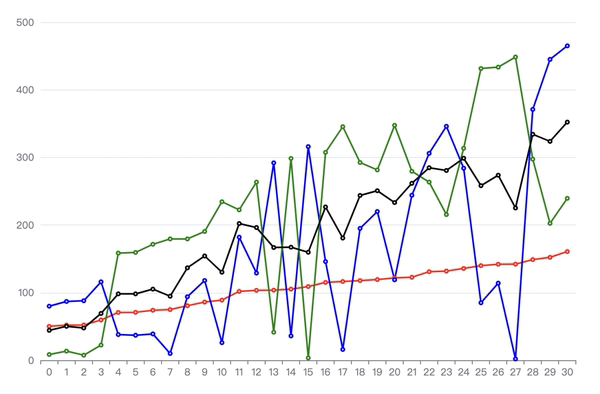
图 17

4 . 最小二乘法

拟合一条曲线的一种方法就是最小二乘法，原理这里就不介绍了。总之，假定红色折线可以通过 z = ax + by 的形式由蓝色折线和绿色折线拟合的话，最小二乘法可以帮我们求出最准确的 a 和 b。

import numpy as np
from scipy import optimize        # 最小二乘法拟合


def func(x, y, p):
    """ 数据拟合所用的函数：z=ax+by
    :param x: 自变量 x
    :param y: 自变量 y
    :param p: 拟合参数 a, b
    """
    a, b = p
    return a * x + b * y

def residuals(p, z, x, y):
    """ 得到数据 z 和拟合函数之间的差
    """
    return z - func(x, y, p)

xSource = [80, 87, 88, 116, 38, 37, 39, 10, 94, 118, 26, 182, 129, 292, 36, 316, 146, 16, 195, 220, 119, 244, 306, 346, 284, 85, 114, 2, 371, 445, 465]
ySource = [8.5, 13.5, 7.5, 22.5, 158.5, 159.5, 171.5, 179.5, 179.5, 190.5, 234.5, 222.5, 263.5, 41.5, 298.5, 3.5, 307.5, 345.5, 292.5, 281.5, 347.5, 279.5, 263.5, 215.5, 313.5, 431.5, 433.5, 448.5, 297.5, 202.5, 239.5]
cSource = [50.11, 52.01, 52.07, 59.54, 70.74, 70.93, 73.96, 74.94, 80.65, 86.02, 88.98, 101.86, 103.34, 103.73, 105.16, 109.0, 115.1, 116.46, 117.88, 119.31, 121.82, 122.75, 130.95, 131.9, 135.75, 139.94, 142.05, 142.12, 148.88, 152.22, 160.76]


def main():

  x = np.array(xSource)
  y = np.array(ySource)
  z = np.array(cSource)  # 数据随便取的

  plsq = optimize.leastsq(residuals, np.array([0, 0]), args=(z, x, y))  # 最小二乘法拟合
    # [0, 0] 为参数 a, b 初始值

  a, b = plsq[0]  # 获得拟合结果
  print("what >>>>>")
  print("拟合结果:\na = {}".format(a))
  print("b = {}".format(b))

main()

得出 a = 0.22320872185884902 , b = 0.28534578186377385，对应到图上是如下效果。红色折线为目标折线，黑色折线为拟合结果。

图 18

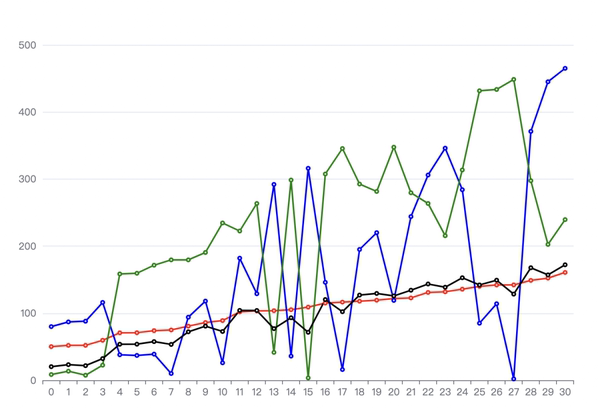
图 18

有了 a 和 b，也就有了贝塞尔曲线的控制点的计算方法。让我们再回到画布中看一看。

实际效果

对比上一节 “有待改进” 中的遗留问题，如下图所示。可以发现，通过修改贝塞尔曲线控制点的计算方式我们已经完美解决了上一节中的遗留问题。

图 19

展望未来

目前仍遗留的问题在于，我们仅知其然，还不知其所以然。我们能提供图编辑场景下的最好的贝塞尔曲线形状，但暂时还不明确控制点对于曲线形状影响的规律该如何描述，也就无法提供任意形状（风格）的贝塞尔曲线。将来可以考虑制作一个小工具，先让用户拖拽控制点，生成若干条某种风格的曲线，然后通过程序从中推断出控制点的计算方式，输出给用户。

总结

我们针对图编辑场景中的连线优化问题，参考了 AntV X6 示例 和 DataV 蓝图编辑器中的连线方案，通过在贝塞尔曲线两端添加直线以及优化贝塞尔曲线控制点的计算方法优化了曲线形状，与原有的连线方案 -- AntV G6 中的 cubic-vertical 曲线相比，大幅提升了的连线的用户体验。