Fly哥给粉丝肝了一晚上的地球飞星动画!!
前言
最近有粉丝在群里讨论,如何实现可视化大屏中的飞星动画,Fly哥最近也是抽空简单写了下小demo。读完这篇文章你可以学到
- 「球面坐标系」
- 「还有就是三阶贝塞尔曲线」
- 「二维图形转球面」
直接看效果:
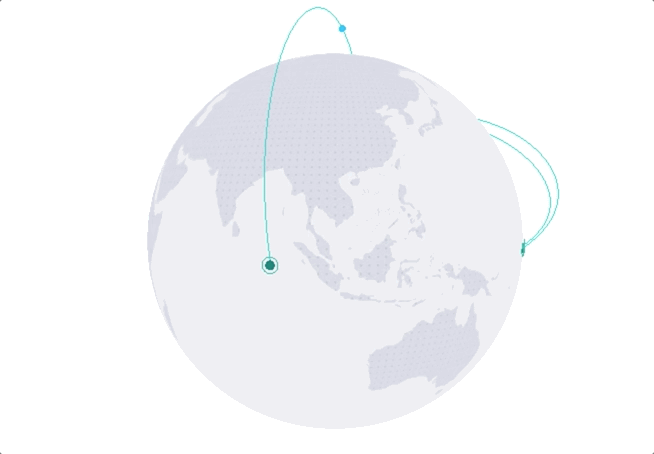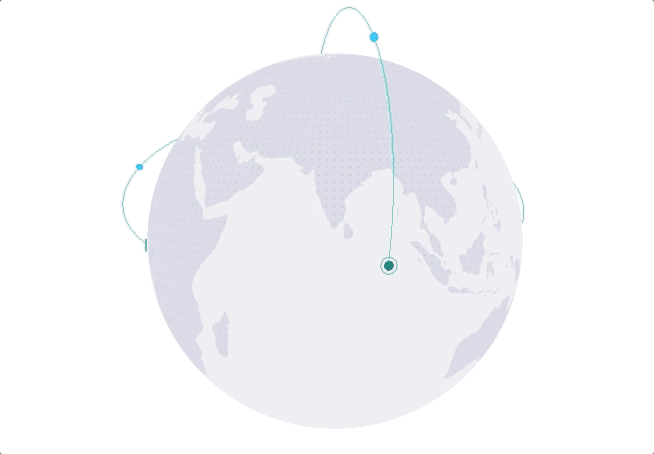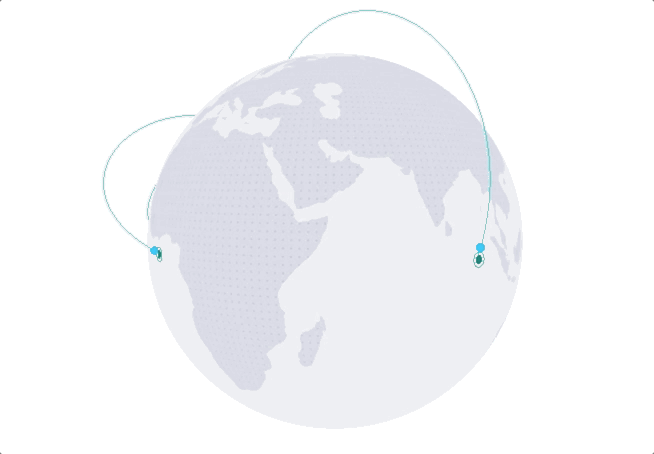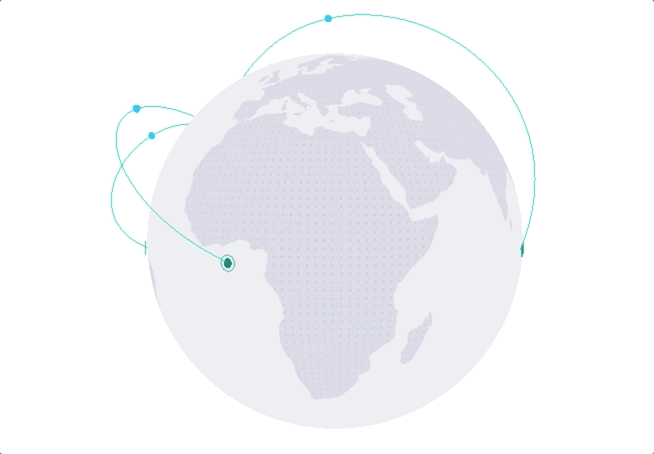
一、 3d绘制场景的构建
绘制一个3d程序首先需要添加 「渲染器」,「场景」,「照相机」 这些元素,这里补充一个灯光;
1、渲染器
首先创建一个渲染器,参数为页面中的canvas元素,
渲染器的作用就是把3d场景的内容结合照相机渲染到页面中,
最后将画布背景设为白色。
const renderer = new Three.WebGLRenderer({canvas: this.$refs.thr});
renderer.setClearColor(0x000000);2、场景
场景顾名思义,就是添加一个你发挥(绘制)的场地,后面所有绘制的元素都要添加到场景中;
cosnt scene = new Three.Scene();
3、照相机
照相机就像人的视觉或说从什么角度去看场景,看场景的位置和视线的方向决定了渲染到页面的内容。故一般需要设置两个参数相机位置position、视线方向lookAt,,在webgl其实是需要三组参数视点,观察点,和上方向。thresjs中好像是默认Y轴为上方向了,这里使用透视相机。
const camera = new THREE.PerspectiveCamera(45, 500 / 500, 1, 1500);
camera.position.set(100, 100, 1000);
camera.lookAt(new THREE.Vector3(0, 0, 0));
scene.add(this.camera);4、灯光
这里使用THREE.HemisphereLight光,可以更加贴近自然的户外光照效;
let light = new THREE.HemisphereLight(0xffffff);
light.position.set(0, 0, 200);
scene.add(light)以上我们基本的绘制要素已添加完成,下面开始绘制各个几何体内容;
「几何体的绘制有三部:创建几何体,创建材料,添加网格模型;」
二、地球的绘制
threejs中提供了球体的绘制,我们只需创建一个球体,材料使用纹理贴图方式添加地图;
贴图图片是我从官网上找的
const geometry = new THREE.SphereGeometry(this.radius, 100, 100); // 球体
const textureLoader = new THREE.TextureLoader(); // 创建纹理贴图
const texture = textureLoader.load(require("@/assets/map.jpg"),texture => {
let material = new THREE.MeshLambertMaterial({map: texture,transparent: true,});
let mesh = new THREE.Mesh(geometry, material);
scene.add(mesh);
});
由于图片加载是异步的 ,这里需等图片加载完成后才能创建材质;

这里我们就创建好了一个地球模型,接着还要让其转动起来;(中间为xyz坐标轴)
threejs提供了几何体的基本3d变换,直接使用rotateY(angleChange)根据时间设置其绕y轴(绿色轴)旋转角度即可;
三、球面坐标点的绘制
「1、在绘制球面位置点时,需先前先看下球坐标系,确定点的位置,webgl中坐标方向与下图不一致,但是对点的表示方法是一致的;」
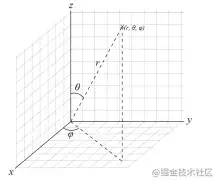
球面上任意点可以用r,θ,φ表示,也可通过以下公式转化到直角坐标系中
x=rsinθcosφ.
y=rsinθsinφ.
z=rcosθ
但实际中地球位置我们一般也会使用经纬度表示。。。下面写个经纬度转坐标的方法。
threejs提供了THREE.Math.degToRad方法可以将经纬度转化为θ,φ,转化方法如下,这里为了方便后面使用,我直接返回一个3维向量;
getPosition(longitude, latitude, radius = this.radius) {
// 经度,纬度转换为坐标
let lg = THREE.Math.degToRad(longitude);
let lt = THREE.Math.degToRad(latitude); // 获取x,y,z坐标
let temp = radius * Math.cos(lt);
let x = temp * Math.sin(lg);
let y = radius * Math.sin(lt);
let z = temp * Math.cos(lg);
return new THREE.Vector3(x, y, z);
},「2、知道了位置的表示方法后开始绘制表示位置的点」
根据示例位置点的由点和一个圆环组成,我们先绘制一个二维平面内的点和圆弧,在通过设置其位置和旋转方式移动到目标坐标位置点;
(这里也可以绘制几何小球体来模拟)
(1)点的绘制
THREE.Shape是用来绘制二维平面内的形状的,设置其形状为圆弧,即可实现一个原点;
let shapePoint = new THREE.Shape();
shapePoint.absarc(0, 0, r - 4, 0, 2 * Math.PI, false);
let arcGeometry = new THREE.ShapeGeometry(shapePoint);
let arcMaterial = new THREE.MeshBasicMaterial({ color: 0x008080 });
let point = new THREE.Mesh(arcGeometry, arcMaterial);
(2)圆弧的绘制
let geometryLine = new THREE.Geometry();
let arc = new THREE.ArcCurve(0, 0, r, 0, 2 * Math.PI);
let points = arc.getPoints(40);
geometryLine.setFromPoints(points);
let LineMateri = new THREE.LineBasicMaterial({ color: 0x20b2aa });
let line = new THREE.Line(geometryLine, LineMateri);
(3)位置的设置
position.set(pos.x, pos.y, pos.z);
(4)二维图形旋转至球面
THREE.Spherical()方法 ,可将坐标点转化为坐标点转化回球坐标系的偏移角度;
let spherical = new THREE.Spherical();
spherical.setFromCartesianCoords(pos.x, pos.y, pos.z);设置位置点旋转
Point.rotateX(spherical.phi - Math.PI / 2);
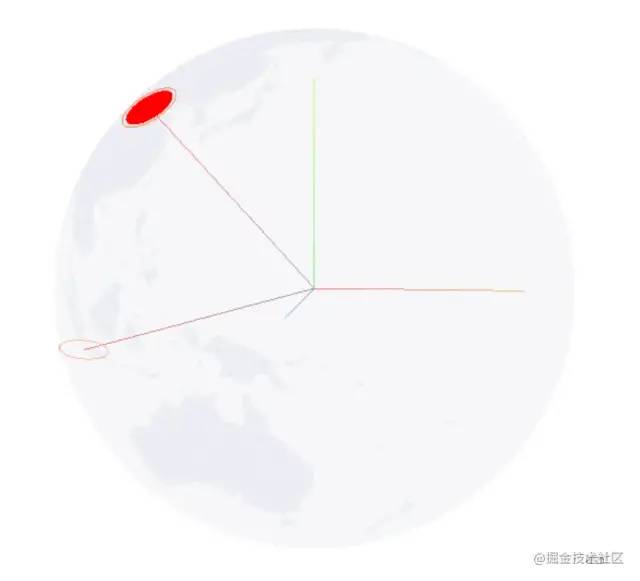
Point.rotateY(spherical.theta);这里为什么要 - Math.PI / 2 是因为开始我们绘制时,平面是垂直于y轴的平面,看下面这幅图吧;
四、接着绘制链接球面两点间的连线
连接两点的曲线需在球面上方,
两点间可以坐出无数条曲线,那么如何确定曲线,我们需自己再选择合适的参数来确定;
首先想的是二阶贝塞尔曲线,取两点的中点为控制点,但如果链接两点刚好位于球面的两个对称端点(两点间连线为直径)时,控制点需在无穷远处;
故考虑使用三阶贝塞尔曲线,连接球面两点和球心,三点确定的一个平面如下图,
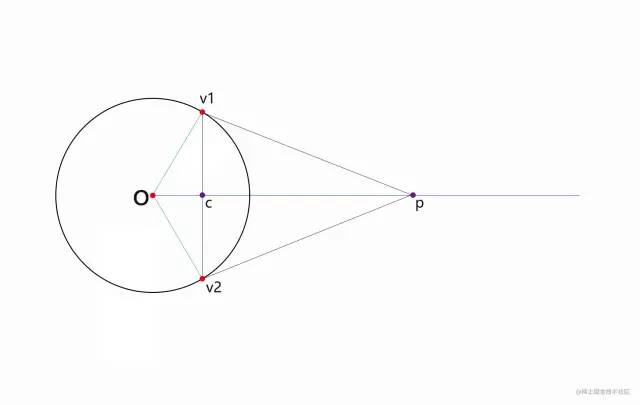
链接v1 v1,取中点c,链接oc,做一条射线,在射线取一点p,链接v1p,v2p,在v1,v2上取两点作为控制点;
求两点的中点
getVCenter(v1, v2) {
let v = v1.add(v2);
return v.divideScalar(2);
}获取两点间指定比例位置坐标
getLenVcetor(v1, v2, len) {
let v1v2Len = v1.distanceTo(v2);
return v1.lerp(v2, len / v1v2Len);
}获取贝塞尔控制点,(控制点位置大小需与夹角线性相关)
// 获取贝塞尔控制点
getBezierPoint(v0, v3) {
let angle = (v0.angleTo(v3) * 180) / Math.PI; // 0 ~ Math.PI // 计算向量夹角
let aLen = angle * 2.5,
hLen = angle * angle * 50;
let p0 = new THREE.Vector3(0, 0, 0); // 法线向量
let rayLine = new THREE.Ray(p0, this.getVCenter(v0.clone(), v3.clone())); // 顶点坐标
let vtop = rayLine.at(hLen / rayLine.at(1).distanceTo(p0), vtop); // 位置
// 控制点坐标
let v1 = this.getLenVcetor(v0.clone(), vtop, aLen);
let v2 = this.getLenVcetor(v3.clone(), vtop, aLen);
return {
v1: v1,
v2: v2
};
},绘制三次贝塞尔曲线
drawLine(longitude, latitude, longitude2, latitude2) {
let geometry = new THREE.Geometry(); //声明一个几何体对象Geometry
let v0 = this.getPosition(longitude, latitude, this.radius);
let v3 = this.getPosition(longitude2, latitude2, this.radius);
let { v1, v2 } = this.getBezierPoint(v0, v3); // 三维二次贝赛尔曲线
let curve = new THREE.CubicBezierCurve3(v0, v1, v2, v3);
let curvePoints = curve.getPoints(100);
geometry.setFromPoints(curvePoints);
let material = new THREE.LineBasicMaterial({ color: 0xff7e41 });
let line = new THREE.Line(geometry, material);
this.group.add(line);
this.sport(curvePoints);
},
五、小球的运动轨迹
小球的动画我们使用three的帧动画,路径可以直接使用上一步中的曲线;
1、绘制小球
drawSportPoint(position, name) {
let box = new THREE.SphereGeometry(6, 6, 6);
let material = new THREE.MeshLambertMaterial({ color: 0x00bfff }); //材质对象
let mesh = new THREE.Mesh(box, material);
mesh.name = name;
mesh.position.set(position.x, position.y, position.z);
this.groupBall.add(mesh);
this.group.add(this.groupBall);
return mesh;
},2、让小球动起来
sport(curvePoints, index) {
const Ball = this.drawSportPoint(curvePoints[0]);
let arr = Array.from(Array(101), (v, k) => k); // 生成一个时间序列
let times = new Float32Array(arr);
let posArr = [];
curvePoints.forEach(elem => {
posArr.push(elem.x, elem.y, elem.z);
}); // 创建一个和时间序列相对应的位置坐标系列
let values = new Float32Array(posArr); // 创建一个帧动画的关键帧数据,曲线上的位置序列对应一个时间序列
let posTrack = new THREE.KeyframeTrack("Ball.position", times, values);
let duration = 101;
let clip = new THREE.AnimationClip("default", duration, [posTrack]);
this.mixer = new THREE.AnimationMixer(Ball);
let AnimationAction = this.mixer.clipAction(clip);
AnimationAction.timeScale = 20;
AnimationAction.play();
},
3、在requestAnimationFrame中添加触发动画
this.mixer.update(this.clock.getDelta());