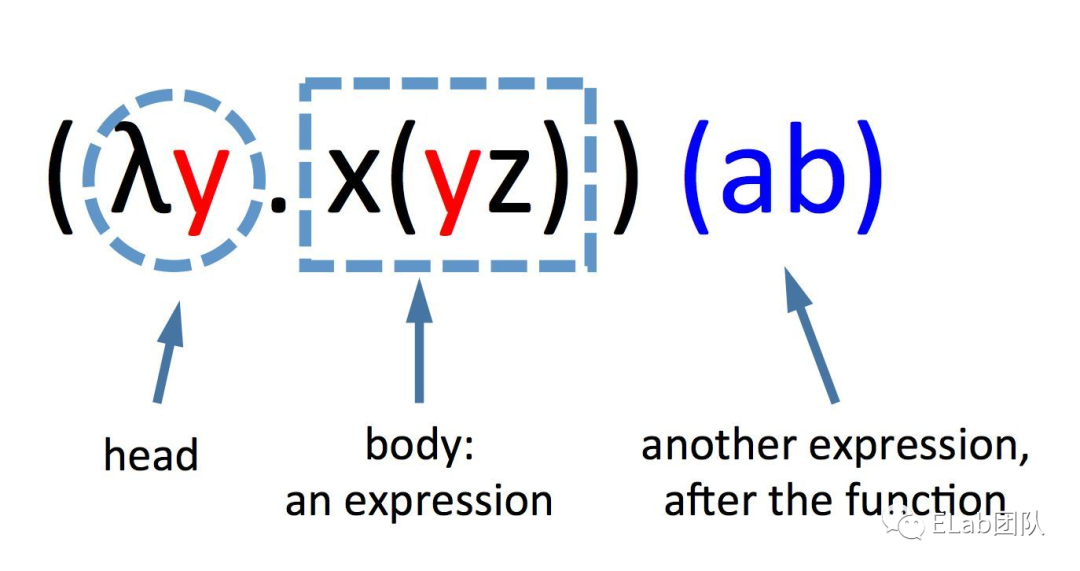
Lambda 演算基础
介绍
λ演算是一套从数学逻辑中发展,以变量绑定和替换的规则,来研究函数如何抽象化定义、函数如何被应用以及递归的形式系统。它由数学家阿隆佐·邱奇在20世纪30年代首次发表。lambda演算作为一种广泛用途的计算模型,可以清晰地定义什么是一个可计算函数,而任何可计算函数都能以这种形式表达和求值,它能模拟单一磁带图灵机的计算过程;尽管如此,lambda演算强调的是变换规则的运用,而非实现它们的具体机器。
语法规则
| 语法 | 名称 | 例子 | 说明 |
|---|---|---|---|
| 变量(variable) | x | 名称为 x 的变量 | |
| λ. | 函数(function) | λx.x | 一个完整的函数定义, 形参为x, 主体为 x. |
| 应用(application) | M N | 将函数 M 作用于参数 N |
自由变量和绑定变量
λx.xy, 其中 x 是绑定变量, y 是自由变量
规则
α 变换
alpha 变换, 即函数变量名可以随意替换, 主要是为了解决表达式中变量名冲突的问题。(注: ≡ 这个符号表示全等,完全等价)
λx.x ≡ λy.y
// js
(x => x) === (y => y)β 归约
用实参替换函数中的形参, 也就是将函数抽象应用于参数的过程, 也就是函数调用。
(λx.x)y ≡ y
(λx.x y)(a(b)) ≡ a b y
// js
(x => x)(y) === y
(x => x)(a(b)) === a(b)对于 (λx.x y)((λz.z)s) 这种表达式, 你可以先对 (λz.z)s 进行 β 规约, 然后再对λx.x y β 规约, 也可以先对λx.x y β 规约, 然后再对(λz.z)s做 β 规约。因为都是纯函数不产生副作用,所以他们顺序无关。
η 变换
有这样的一个函数 λx.M x 将它应用于参数 N, (λx.M x)N. β 规约后变成 M N, 这说明 M ≡ (λx.M x).
对于 λx.M x,其中表达式 M 不包含绑定变量 x 的函数抽象,那么它是冗余的, 这个化简的过程我们叫作 eta 变换。它一般用于清除 λ 表达式中存在的冗余函数抽象。
let fn = (a) => ((b) => 'foo'))(a)
let fn2 = () => 'foo'
fn(1) // 'foo'
fn2() // 'foo'避免歧义
例如对于 λx.x y, 根据语法, 它可以表示 (λx.x)y, 也可以表示 λx.(x y).
除了使用括号让表达式更加明确, 我们也可以定义两个消除歧义的约定:
- 一个函数抽象的函数体将尽最大可能向右扩展,就是说
λx.x y代表的是一个函数抽象λx.(x y)而非函数应用(λx.x)y - 函数应用是左结合的,
X Y Z意为(X Y) Z而非X (Y Z)
为了方便阅读, 我会用空格分割变量,对于 λx.M(N)这样的函数, 有些地方会写成这样 λx.M N.
下文出现let M = λx.x这样写的地方,表示 M 是这个 λx.x 函数的别名。
另外,如果 λ 表达式当中出现一个大写的变量,则表示它是一个函数别名。
柯里化
Lambda 演算中的函数,只能接收一个参数。那么对于一个加法函数, 它应该写成这样
λa.λb.PLUS a b
// js
const fn = a => b => PLUS(a, b)由于 Lambda 演算中只有函数, 没有运算符, 所以这里我们用 PLUS 这个函数表示将两数相加。
通过柯里化, 我们可以很容易的将一个多参函数转换成单参函数。
const curry = (f) => {
let args = [];
const g = (x) => {
args.push(x)
if (args.length === f.length) {
return f(...args)
} else {
return g
}
}
return g
}
const plus = (a, b) => a + b
const f = curry(plus)
f(1)(2) // 3在 λ 表达式中函数单参形式可读性不如多参形式,有了柯里化帮我们转化,因此为了可读性,下文的 λ 表达式中的函数会写成多参的形式。
条件分支
在 js 当中, 我们有三目运算符
(condition, a, b) => condition ? a : b
在上面这个函数当中, 我们发现, 如果返回值为 a, 则说明 condition 是 true。若返回值为 b,则 condition 为 false.
于是, 在 lambda 中, 我们可以这样定义 Bool。如果一个函数接收两个参数,它永远返回第一个参数的话就认为是 TRUE,永远返回第二个参数的话就我们认为是 FALSE
let TRUE = λx y.x
let FALSE = λx y.y
let TRUE = (x, y) => x
let FALSE = (x, y) => y现在我们可以写一个 IF 函数,它的第一个参数是一个条件表达式,第二个参数是如果条件为真时才进行运算的表达式,第三个参数则如果条件为假时要进行的运算。
let IF = λc t f.c t f
(IF)(TRUE a b)
≡ (λc t f.c t f)(TRUE a b)
≡ TRUE a b
≡ (λx y.x)(a b)
≡ a
// js
(a, b) => true ? a : b
(a, b) => ((x, y) => x)(a, b)我们可以继续定义与或非
let AND = λx y.x y FALSE
let OR = λx y.x TRUE y
let NOT = λx.x FALSE TRUE
// 例子
AND TRUE FALSE
≡ (λx y.x y FALSE)(TRUE FALSE)
≡ TRUE FALSE FALSE
≡ (λx y.x)(FALSE FALSE)
≡ FALSE
OR FALSE TRUE
≡(λx y.x TRUE y)(FALSE TRUE)
≡ FALSE TRUE TRUE
≡ (λx y.x)(TRUE FALSE)
≡ TRUE
NOT TRUE
≡ (λx.x FALSE TRUE)(TRUE)
≡ TRUE FALSE TRUE
≡ (λx y.x)(FALSE TRUE)
≡ FALSE
NOT FALSE
≡ (λx.x FALSE TRUE)(FALSE)
≡ FALSE FALSE TRUE
≡ (λx y.y)(FALSE TRUE)
≡ TRUE丘奇数
前面我们已经定义了布尔值和一些逻辑运算符, 接下来我们来定义下自然数。
自然数的定义可以参考皮亚诺公理[1]。
皮亚诺的这五条公理用非形式化的方法叙述如下:
- 0是自然数;
- 每一个确定的自然数a,都有一个确定的后继数a' ,a' 也是自然数;
- 对于每个自然数b、c,b=c当且仅当b的后继数=c的后继数;
- 0不是任何自然数的后继数;
- 任意关于自然数的命题,如果证明:它对自然数0是真的,且假定它对自然数a为真时,可以证明对a' 也真。那么,命题对所有自然数都真。
简单点说就是, 0 是一个自然数, 0 有一个确定的后继数 1, 1 有一个确定的后继数 2. 以此类推...
现在我们可以定义一个后继函数 S, 它接收一个自然数, 并且返回这个自然数的后继。那么自然数就能用下面的方法来表示
0
1 = S(0)
2 = S(1) = S(S(0))
3 = S(2) = S(S(1)) = S(S(S(0)))
// ...在 lambda 演算中, 我们可以这样表示上述代码
let ZERO = λs z.z
let ONE = λs z.s(z)
let TWO = λs z.s(s(z))
let THREE = λs z.s(s(s(z)))一个很好的理解办法是将 z 作为是对于零值的命名,而 s 作为后继函数的名称。
因此,0 是一个仅返回 “0” 值的函数;1是将后继函数运用到0上一次的函数;
2则是将后继函数应用到0的后继上的函数,以此类推。
用 js 我们这样表示
let ZERO = (s, z) => z
let ONE = (s, z) => s(z)
let TWO = (s, z) => s(s(z))
let THREE = (s, z) => s(s(s(z)))
let s = n => n + 1
let convert = f => f(s, 0)
convert(ZERO) // ZERO(s, 0) === 1
convert(ONE) // ONE(s, 0) === 1
convert(TWO) // TWO(s, 0) === 1
convert(THREE) // THREE(s, 0) === 1要得到自然数 N, 我们只要将后继函数 S 应用到 0 上 N 次即可。
上面的 ONE, TWO, THREE 都是我们手动列出来的。
我们的 ONE 应该要能通过 S(ZERO) 得到。
这里的后继函数 S 用 λ 表达式可以表示为
let S = λx y z.y(x y z)
S(ZERO)
≡ (λx y z.y(x y z)) (λ sz.z) // α 变换: (λ ab.b) = (λ sz.z)
≡ (λx y z.y(x y z)) (λ ab.b) // β 规约: x = (λ ab.b)
≡ λy z.y((λ ab.b) y z) // β 规约: a = y, b = z
≡ λy z.y(z) // // α 变换: λs z.s(z) = λy z.y(z)
≡ λs z.s(z) // ONE
// js
let s = n => n + 1
let convert = f => f(s)(0)
let S = n => (s, z) => s(n(s, z))
let ONE = S(ZERO)
convert(ONE) // 1加法
有了数以后,我们还要定义加减乘除。
加法的含义是, 对于 2 + 3 = 5, 我们只要对 2 使用 3 次 S 即可得到 5.
let PLUS = λx y s z.x s (y s z)
≡ λx y.λs z.x s (y s z)
let TWO = λs z.s(s(z))
let THREE = λs z.s(s(s(z)))
PLUS TWO THREE
≡ (λx y.λs z.x s (y s z))(TWO THREE) // β 规约: x = TWO, y = THREE
≡ λs z.TWO s (THREE s z) // 替换别名, 同时做 α 变换
≡ λs z.(λs2 z2.s2(s2(z2))) s ((λs3 z3.s3(s3(s3(z3)))) s z) // β 规约:s3 = s, z3 = z
≡ λs z.(λs2 z2.s2(s2(z2))) s (s(s(s(z)))) // β 规约:s2 = s, z2 = s(s(s(z)))
≡ λs z.s(s(s(s(s(z)))))
// js
let PLUS = (x, y) => (s, z) => x(s, y(s, z))
let TWO = (s, z) => s(s(z))
let THREE = (s, z) => s(s(s(z)))
let s = n => n + 1
let convert = f => f(s, 0)
let FIVE = PLUS(TWO, THREE)
convert(FIVE) // 5
// 柯里化版本
let PLUS = x => y => s => z => x(s)(y(s)(z))
let TWO = s => z => s(s(z))
let THREE = s => z => s(s(s(z)))
let s = n => n + 1
let convert = f => f(s)(0)
let FIVE = PLUS(TWO)(THREE)
convert(FIVE) // 5加法还有另外一种定义方法 let`` PLUS = λx y.x S y. 这两种方法是等价的
let PLUS = λx y.x S y
≡ λx y.x (λa s z.s(a s z)) y
≡ λx y.x (λs z.s(y s z))
≡ λx y.λs z.x s (y s z) // 这里和前面的定义加法函数一模一样
PLUS ONE TWO
≡ (λx y.x S y) (ONE TWO)
≡ ONE S TWO
≡ ONE (λx y z.y(x y z)) TWO
≡ ONE (λa b c.b(a b c)) TWO
≡ (λs1 z1.s1(z1)) (λa b c.b(a b c)) (λs2 z2.s2(s2(z2)))
≡ (λa b c.b(a b c)) (λs2 z2.s2(s2 z2)) // s1 = (λa b c.b(a b c)) , // z1 = (λs2 z2.s2(s2 z2))
≡ b((λs2 z2.s2(s2(z2))) b c) // a = (λs2 z2.s2(s2 z2))
≡ b(b(b(c))) // s2 = b, z2 = c
≡ s(s(s)(z)) // => THREE乘法
let MULTIPLY = λx y s.x(y s)
MULTIPLY ONE TWO
≡ (λx y s.x(y s)) (ONE TWO)
≡ λs.ONE(TWO s) // β: x = ONE, y = TWO
≡ λs.(λs1 z1.s1(z1)) (λs2 z2.s2(s2(z2)) s) // 别名替换,同时做 α 变换和 β: s2 = s
≡ λs.(λs1 z1.s1(z1)) (λz2.s(s(z2))) // β: s1 = (λz2.s(s(z2)))
≡ λs.λz1.(λz2.s(s(z2)))(z1) // β: z2 = z1
≡ λs.λz1.s(s(z1)) // α: λz.s(s(z)) = λz1.s(s(z1))
≡ λs.λz.s(s(z)) // TWO更多函数定义可以参考下图
循环
首先,所有的循环都可以用递归代替。是否所有的循环都能用递归代替? - 知乎[2]
递归的含义是「函数直接或间接的调用自身」,在编程语言中,函数要调用自身就要持有一个「自身的引用」,这个引用就是函数名。
而在 lambda 演算中,所有函数都是匿名函数,那么如何引用自身?
答案是 Y Combinator。
Y Combinator 用于计算(高阶)函数的不动点,这使得一个匿名函数可以通过 Y Combinator 得到自身,之后再调用自身,从而实现递归。
不动点
函数 f 的不动点是将函数应用在输入值 x 时,会传回与输入值相同的值,使得 f(x) = x。例如,0 和 1 是函数 f(x) = x^2 的不动点,因为 0^2 = 0 而 1^2 = 1。鉴于一阶函数(在简单值比如整数上的函数)的不动点是个一阶值,高阶函数 f 的不动点是另一个函数 g 使得 f(g) = g。Y 组合子可以计算出这个不动点 g,那么 g = y(f),将 g 代入我们可以得到 y(f) = f(y(f))。
Y Combinator 简介
Y Combinator 是由 Haskell B. Curry[3] 发现的。它用 λ 表达式表示的话长这样 λf.λx.(f(x x))(λx.(f(x x)))
// 写成 js 的话
(function (f) {
return (function (x) {
return f(x(x))
})(function (x) {
return f(x(x))
})
})
// 写成箭头函数
( f => (x => f(x(x)))(x => f(x(x))))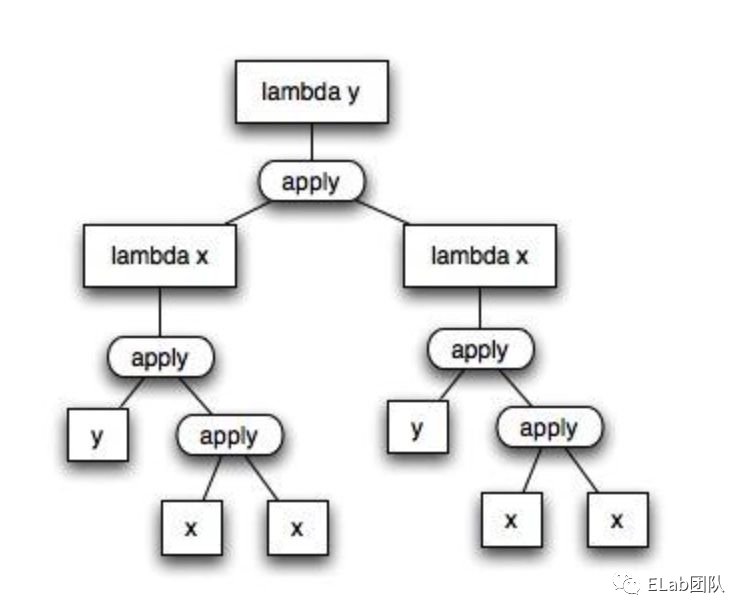
Y Combinator 推导过程
// 1. 一个朴素的计算阶乘的函数 f
// 如果它是一个匿名函数,没有名字,那么如何递归调用自身?
// 有个同学会说可以使用 arguments.callee, 但是对于箭头函数,是没有 arguments 对象的
function f(n) {
if (n === 1) {
return 1
}
return n * f(n - 1)
}
// 2. 我们将它改成匿名函数,现在我们无法通过函数名去拿到关于自身的引用
// 既然这样,不如把它变为一个参数,我们通过参数来持有它的引用
function (f, n) {
if (n === 1) {
return 1
}
return n * f(n - 1)
}
// 柯里化后变成这样
function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(n - 1)
}
}
// 你可能会好奇,这有什么用?别着急继续往下看
// 3. 柯里化后,这个匿名函数变成了一个高阶函数,它接受一个可以计算阶乘的函数 f。
// 这个用来计算阶乘的函数 f, 我们可以将最开始的那个朴素阶乘函数传进来,
// 并且为了便于区分,我们将函数名先改成 g
(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(n - 1)
}
})(function g(n) {
if (n === 1) {
return 1
}
return n * g(n - 1)
})
// 然后你会发现,这里的实参函数仍然有一个函数名 g,
// 因此和前面的做法一样,我们也将它变成一个匿名函数,使得 g 通过参数传进来
(function (f) {
return function (n) {
if (n === 1) {
return 1
}
// 由于传进来的函数现在接收两个参数,因此这里调用方式变了
// 从 n * f(n - 1) 变成 n * f(, n - 1)
// 那么,这里的 我们应该传什么?
return n * f(,n - 1)
}
})(function (g, n) {
if (n === 1) {
return 1
}
return n * g(n - 1)
})
// 我们回过头来看现在的实参函数,它是一个匿名函数且需要两个参数,
// 第一个参数 g 是个可以计算阶乘的函数,第二个参数是要计算阶乘的数
// 所以 这里填的是应该是个计算阶乘的函数
// 但是,我们现在的这个实参函数,不就可以用来计算阶乘吗?
// 实参传进来后变成形参 f,那么 这里应该是 f
(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f, n - 1)
}
})(function (g, n) {
if (n === 1) {
return 1
}
return n * g(n - 1)
})
// 然后我们在看下 n * f(f, n - 1),当我们执行到这里时,我们进入到实参函数内部的逻辑
function (g, n) {
if (n === 1) {
return 1
}
return n * g(n - 1)
}
// 此时接收到的形参 g 是它自身!它自身是需要两个参数的,所以 n * g(n - 1) 的调用方式也需要修改
// 从 n * g(n - 1) 变成 n * g(, n - 1)
// 这里的 也是一个计算阶乘的函数,那么逻辑同上,因此需要改成 n * g(g, n - 1)
// 于是我们得到了
(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f, n - 1)
}
})(function (g, n) {
if (n === 1) {
return 1
}
return n * g(g, n - 1)
})
// 4. 现在,我们再将实参函数进行柯里化,并且将函数名修改回原本的 f,即有:
(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})
// 现在我们可以先验证一下,将以下这段代码复制到浏览器 console 里运行,你会得到 120
(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})(5)
// 5. 我们继续,我们在上一步的结果外面包一层 IIFE, 显然,这对逻辑没有什么影响,看起来好像没什么作用
(function () {
(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})
})()
// 6. 这时候我们会发现有,有两个地方的代码一模一样,我们可以将这部分代码提取出来
// 通过参数传进来,于是就得到了
(function (g) {
// 原本这里的一大坨都提到外面去啦,变成了参数 g
return g(g)
})(function (f) {
return function (n) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})
// 7. 然后我们对在实参内部,在做两层 IIFE 包装
const r = (function (g) {
return g(g)
})(function (f) {
// 为了方便阅读和理解,这里标注了类型
return function (x: number) {
return (function () {
// 这外面包了两层 IIFE
return function (n: number) {
if (n === 1) {
return 1
}
return n * f(f)(n - 1)
}
})()(x)
}
})
// 8. f(f) 返回的是一个阶乘函数, 也就是我们前面高阶函数返回的函数啦,将它提取成参数
(function (g) {
return g(g)
})(function (f) {
return function (x: number) {
return (function (factorial: (n:number) => number) {
return function (n) {
if (n === 1) {
return 1
}
return n * factorial(n - 1)
}
})(f(f))(x)
}
})(5)
// 9. 我们发现 function (factorial) { ... } 这部分代码是写死的
// 我们要推导的 y 组合子是一个通用的高阶函数,因此把这部分代码再提取出来
// 提取方法是最外面在包装一个函数, 将 function (factorial) { ... } 作为参数 h 传进来
function (h) {
return (function (g) {
return g(g)
})(function (f) {
return function (n) {
return h(f(f))(n)
}
})
}(function (factorial) {
return function (n) {
if (n === 1) {
return 1
}
return n * factorial(n - 1)
}
})
// 10. 由于提取成实参后也是一个高阶函数,因此将 g(g) 这个地方需要修改成 h(g(g))
function (h) {
return (function (g) {
return h(g(g))
})(function (f) {
return function (n) {
return h(f(f))(n)
}
})
}(function (factorial) {
return function (n) {
if (n === 1) {
return 1
}
return n * factorial(n - 1)
}
})
// 修改下变量名, h -> f, g -> x, 得到的即为 y combinator
// 复制下面这段代码在 console 试试
const y = function (f) {
return (function (x) {
return f(x(x))
})(function (x) {
return function (n) {
return f(x(x))(n)
}
})
}
const fa = y(function (factorial) {
return function (n) {
if (n === 1) {
return 1
}
return n * factorial(n - 1)
}
})
fa(5)
// 11. 你可能会注意到,上一步得到的 y combintor 和我最开始用箭头函数翻译的有些不同
// 前面箭头函数的版本:(f => (x => f(x(x)))(x => f(x(x))))
// 实际上箭头函数的这段代码是不可用的,原因是 js 立即求值导致爆栈,需要将其包装成惰性的
(function (f) {
return (function (x) {
return f(x(x))
})(function (x) {
// 由于 js 是立即求值的, 所以这里会溢出。
// 所以在 js 中这里会被包装一下,
// 即上面 260 行的 function(n) { ... } 匿名函数包装
return f(x(x))
})
})参考资料
[1]皮亚诺公理: https://zh.wikipedia.org/wiki/%E7%9A%AE%E4%BA%9A%E8%AF%BA%E5%85%AC%E7%90%86
[2]是否所有的循环都能用递归代替? - 知乎: https://www.zhihu.com/question/29373492/answer/44137224
[3]Haskell B. Curry: https://en.wikipedia.org/wiki/Haskell_Curry
[4]λ演算(Lambda Calculus)入门基础(一):定义与归约: https://www.jianshu.com/p/ebae04e1e47c
[5]阿隆佐.丘奇的天才之作——lambda演算中的数字: https://cgnail.github.io/academic/lambda-2/
[6]Church encoding - Wikipidia: https://en.wikipedia.org/wiki/Church_encoding
[7]Lambda Calculus - Learn X in Y minutes: https://learnxinyminutes.com/docs/lambda-calculus/
[8]You Can Explain Functional Programming Using Emojis: https://ycombinator.chibicode.com/functional-programming-emojis/
[9]Y-Combinator推导的Golang描述: https://www.jianshu.com/p/d301e0008a2e
[10]Fixed Point Combintor - Wikipedia: https://en.wikipedia.org/wiki/Fixed-point_combinator