一、解决哪些问题

要实现可视化公式编辑器，一般需要解决以下几个问题：

1. 公式如何转化成计算机可以“理解”的数据？这里的“理解”主要针对可视化编辑而言。
2. 计算机“理解”之后，如何对公式进行排版渲染？
3. 解决了排版渲染，又如何进行交互编辑？
4. 解决了交互编辑，如何提升编辑效率？

二、公式的表达

在数学中，广义上的公式是指在特定的形式文法下，把数学符号组合而成之结果。在思考如何表达之前，我们先来看看公式的结构。

2.1 公式结构

总结我们所有学习过的公式，只有两种内容：符号 和 结构。

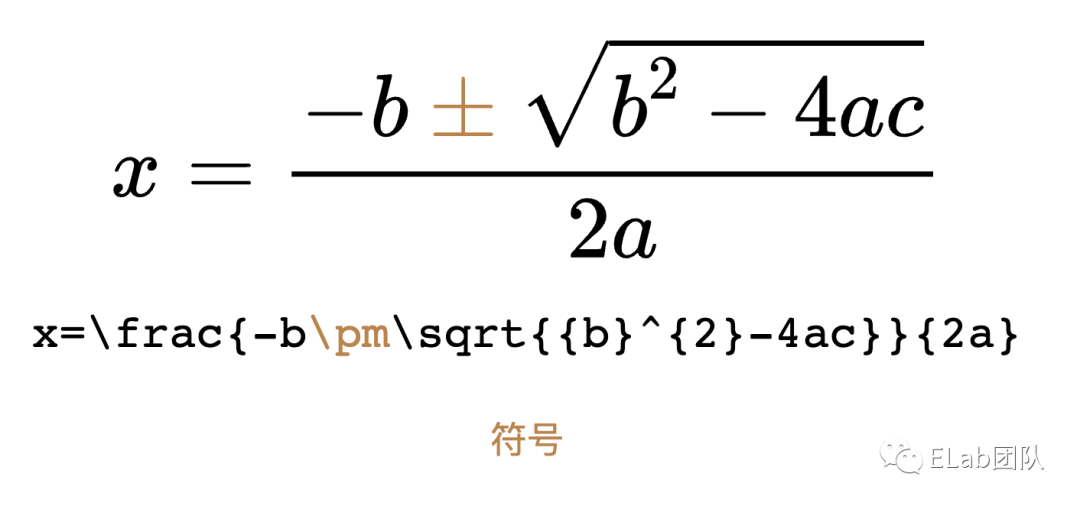
2.2 公式语言

将符号和结构进行定义，在设计上提供结构可嵌套的能力，即可解决公式的计算机程序表达，也就解决了计算机理解公式的问题。这种行为，宽泛来说是在设计一套公式语言。在设计自己的语言之前，我们看看市面上已有的公式语言。市面常用的公式语言有：LaTeX、MathML、OMML、AsciiMath，当然还有 UnicodeMath 等其他不常见的语言。

我们来看看下图公式在各种语言中的表达：

LaTeX

LaTeX （/ˈlɑːtɛx/，常被读作/ˈlɑːtɛk/或/ˈleɪtɛk/，写作“LATEX”）。LaTeX 系统是一种可以处理排版和渲染的标记语言。代码示例x=\frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a}LaTeX 是一套文档排版系统，LaTeX 公式（即 AMS-LaTeX），只是其中一部分，由美国数学会提供。LaTeX 公式为 符号 和 结构 分别定义了一套命令，如\pm代表符号；如 \frac{}{}表示分式结构等。

AsciiMath

AsciiMath 是一种客户端数学标记语言，用于在 Web 浏览器中显示数学表达式。

代码示例：x =（-b +- sqrt（b ^ 2 – 4ac））/（2a）AsciiMath 在 LaTeX 公式基础上有所简化，尽可能使用数学原本的表达。不能表达的符号和结构才使用命令，如sqrt表示根式结构。

MathML

MathML 是一个用于描述数学公式的一种 XML 标记语言，由万维网联盟的数学工作组提出。代码示例：

<math display="block">
  <mi>x</mi>
  <mo>=</mo>
  <mrow>
    <mfrac>
      <mrow>
        <mo>-</mo>
        <mi>b</mi>
        <mo>&#xB1;</mo>
        <msqrt>
          <msup>
            <mi>b</mi>
            <mn>2</mn>
          </msup>
          <mo>&#x2212;</mo>
          <mn>4</mn>
          <mi>a</mi>
          <mi>c</mi>
        </msqrt>
      </mrow>
      <mrow>
        <mn>2</mn>
        <mi>a</mi>
      </mrow>
    </mfrac>
  </mrow>
</math>

MathML 的定义里只涉及公式结构，公式符号由Unicode字符本身去表达。

2.3 为什么选 LaTeX

在以上常用语言中，选用了 LaTeX，原因有以下几点：

• 诞生较早，早于C语言，市场占有率较高、生态较完备，特别是在印刷领域；
• 稳定性好，几十年前的文档都能在现在很好的渲染；
• 开源免费；
• 两位设计者高德纳 ( Donald Knuth )、莱斯利·兰波特 ( Leslie Lamport ) 都是图灵奖得主；
• LaTeX是行业最通用的排版方案，Web 端有较优秀的渲染工具MathJax和KaTeX。

三、公式的渲染

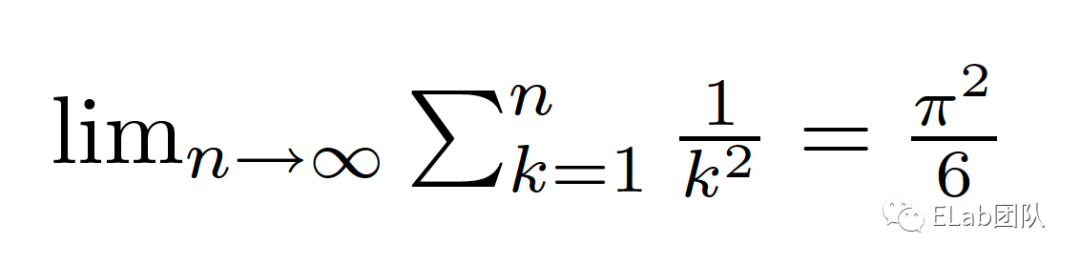
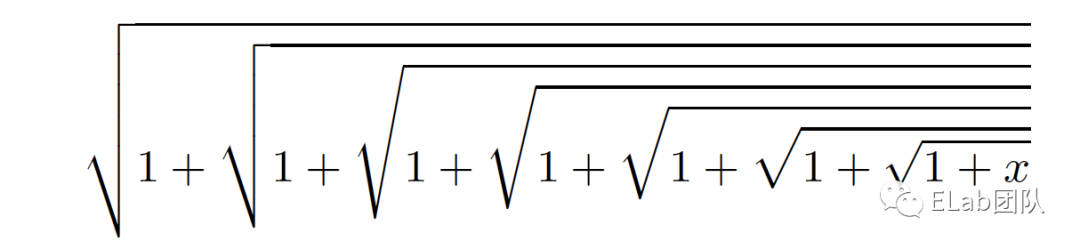
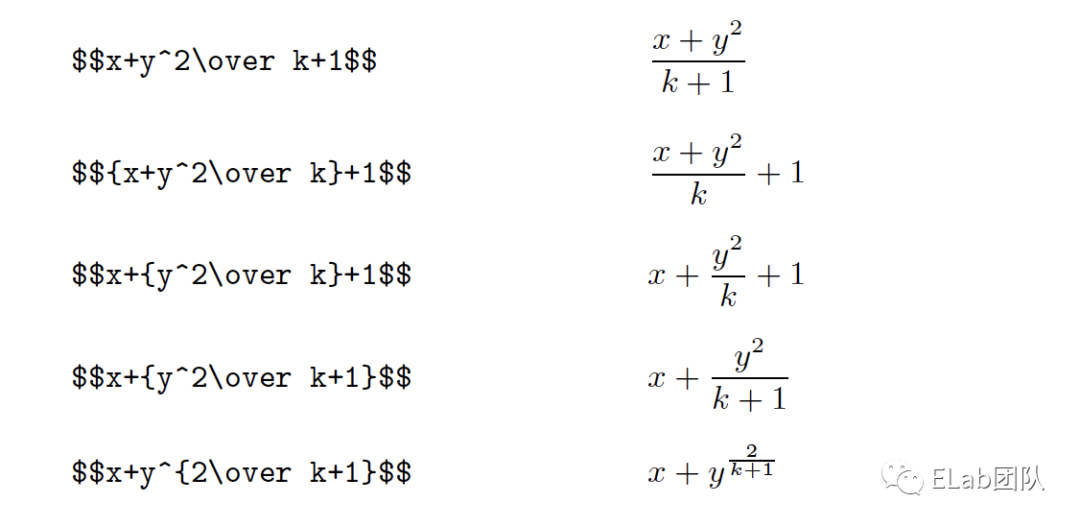
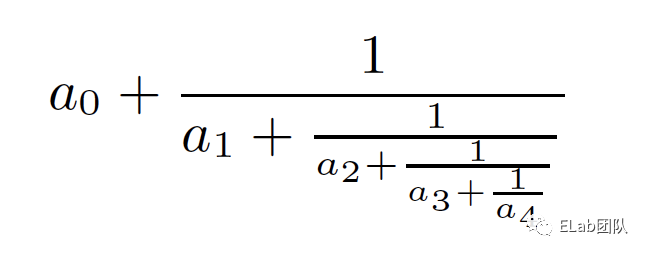
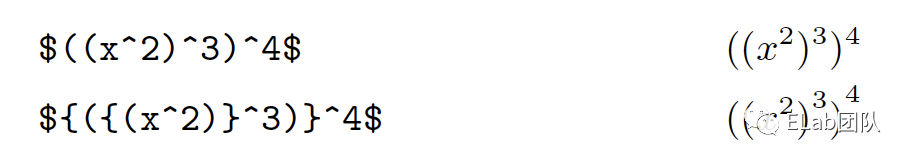
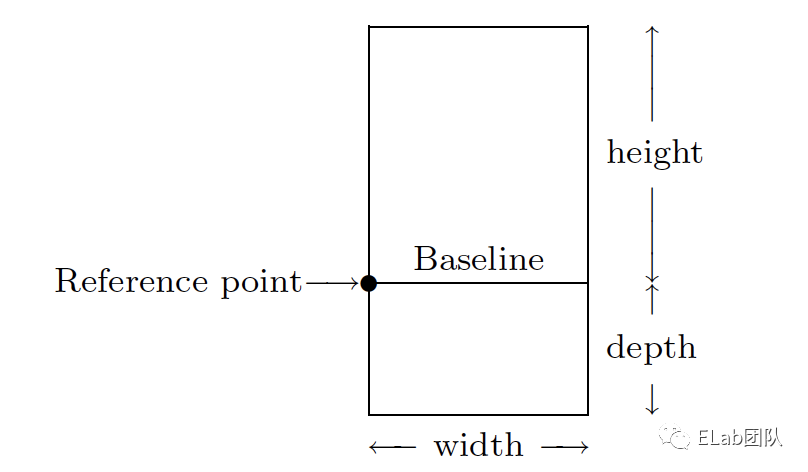
公式渲染解决的是公式在不同载体上的排版问题。先看看几张公式图，对公式排版的一些情况有个感性的认识。 在 LaTeX 中有一套公式渲染规范，为了让公式在各种组合和嵌套的情况下，依然尽可能的保持视觉上的美观，这里摘取两点：盒子模型、四级渲染，简单过一下。完整内容可以阅读 TeXBook 文档。

3.1 盒子模型

TEX 中的盒子是长方形的二维对象, 有三个相应的尺寸, 叫做高度, 宽度和深度。下面是一个标准盒子的样子，其中给出了它的所谓基准点和基线:

3.2 公式的四级渲染

四级渲染是为了解决各种嵌套层级下的公式美观问题，来看个例子：

我们会看到的字体大小要比大。试想一下，如果这个公式继续嵌套下去，该怎么渲染呢？是继续变小吗？四级渲染正式为了解决这类问题。

TeX 定义了渲染的四级：

D 列表字体 公式中最大的字体，主要使用在独占一行的公式中。D （display style），代表行间。

T 文本字体 行内公式的常规字体。T（text style），代表行内。

S 标号字体 一般用于上下角标。S（script style），代表角标。

SS 小标号字体 一般用于角标的角标，如公式中最上面的‘2’。SS（script script style），代表角标的角标。

以及四种其它的“近似”字体 D'、T'、S'、SS'，它们与上面四种几乎一样，只是角标相对主体内容升高没那么多。

也就是说公式中最多 4 中字体大小，这样就不会出现公式某些部分小到看不见的情况。

3.3渲染方案选择

公式渲染要完全遵循 TeXBook 规范，成本非常高。考虑到目前的现状，时间成本，投入产出比，公式渲染方案最终选择了比较成熟的 Web 端公式渲染工具 MathJax。有人会说为什么不选 KaTeX，有关于渲染的另一个因素在里面，接下来会提到。列一下 MathJax 的背景，再给自己点理由。

四、公式的编辑

既然自己实现渲染，成本相对高昂，考虑到效益就只能选择成熟的 MathJax 或 KaTeX 了。也就是说，只能在已有工具渲染的公式DOM上进行交互操作，以实现最终的编辑操作。

4.1 可视化编辑实现

LaTeX 公式，如x=\frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a}，输入渲染工具，渲染工具将其解析并完成渲染：

要在此基础上完成编辑，必须完成以下两个动作才能实现：

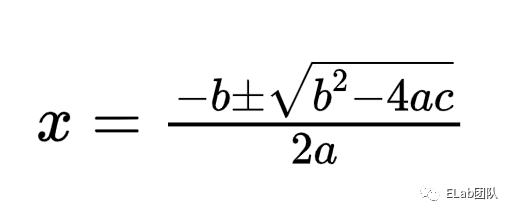
1. 根据用户的光标位置，定位编辑的 LaTeX 公式部位，即实现视觉结构和 LaTeX 代码的完全映射；
2. 用户编辑动作完成，立即更新视觉，同时更新 LaTeX 代码；

经过分析研究 MathJax 和 KaTeX 的渲染机制发现，MathJax 在 DOM 结构上与公式语言 MathML 有高度的相似性，为低成本实现视觉和公式代码的映射带来了可能性。因此设计了如下的公式编辑实现方案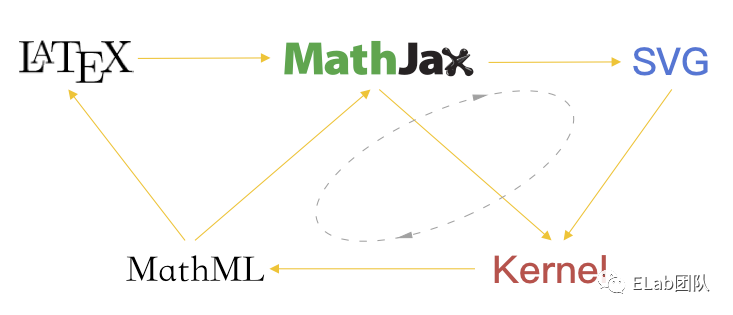： 具体过程如下：

1. LaTeX 或 MathML 公式输入 MathJax；
2. MathJax 解析公式生成 视觉 SVG DOM 的同时，生成基于 MathML 结构的 Kernel，并建立 SVG 和 Kernel 节点的一一映射；
3. 用户操作 SVG DOM 节点时，将其转化为对 Kernel 数据的操作；
4. 利用更新后的 Kernel，生成新的 MathML 公式；
5. 将新的 MathML 公式，再次输入 MathJax，回到第一步。

在此过程中，所有的公式的渲染都是由 MathJax 完成的，因此可以保证渲染的美观性。

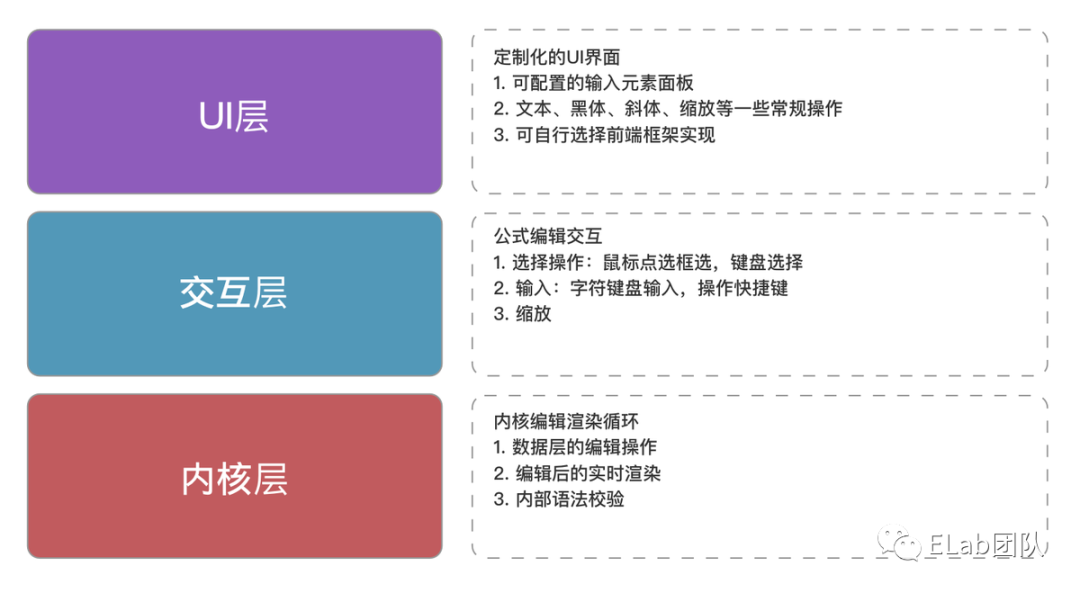
4.2 技术架构设计

在技术架构上，进行了如下设计，充分解耦 UI 层，确保业务上的灵活性，此处大家可以充分自由发挥，不是本文的重点，就不多提了。

五、公式编辑效率优化

5.1 公式编辑的本质

从公式编辑的角度来说，公式是符号和结构的组合。符号如 π、Ω 等；结构如分式（fraction）、根式（square root）等。因此公式编辑的本质，是解决符号和结构的输入问题。效率、便捷性和质量（如语法正确等）是衡量公式编辑能力的关键指标。

5.2 编辑路径分析

5.2.1 关于效率

公式编辑本质是，意识中的公式符号和结构 转换成实物上的表达和展示。如何缩短从意识到实物载体呈现的路径，是有效提高公式编辑效率的主要关注点。

公式元素分为两类符号元素和结构元素，是一个大的集合。一个公式编辑动作需要完成两个步骤，第一步：公式元素检索；第二步，检索结果输入。

编辑的形式主要分为两类，代码编辑和可视化编辑。以下分这两种场景来讨论效率优化。

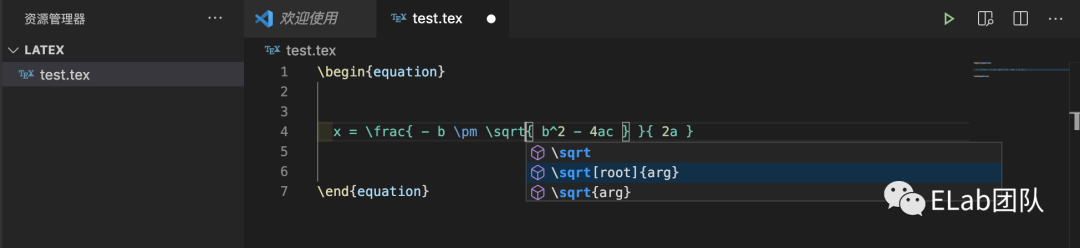
(1)代码编辑

代码编辑，即通过直接输入公式代码来输入公式，如图：

公式元素检索

代码检索更适合熟悉公式语言（如LaTeX）的人群，先要完成公式元素和代码对应关系的记忆，才能有效的完成代码检索。这种方式有一定的记忆成本，但检索快，也最灵活。

大量的记忆有较高的成本，降低记忆成本是此环节的效率优化点。

检索结果输入

代码编辑模式下，检索结果为公式语言代码。如分式（fraction），在LaTeX语言中对应的代码为:\frac{}{}，包含命令\frac，和两个参数{}。纯文本输入会消耗较多的时间。

公式元素在公式语言中，都有固定对应的代码表达，能够一次性输入公式元素对应代码，而非逐字符输入公式元素对应代码，是此环节的效率优化点。

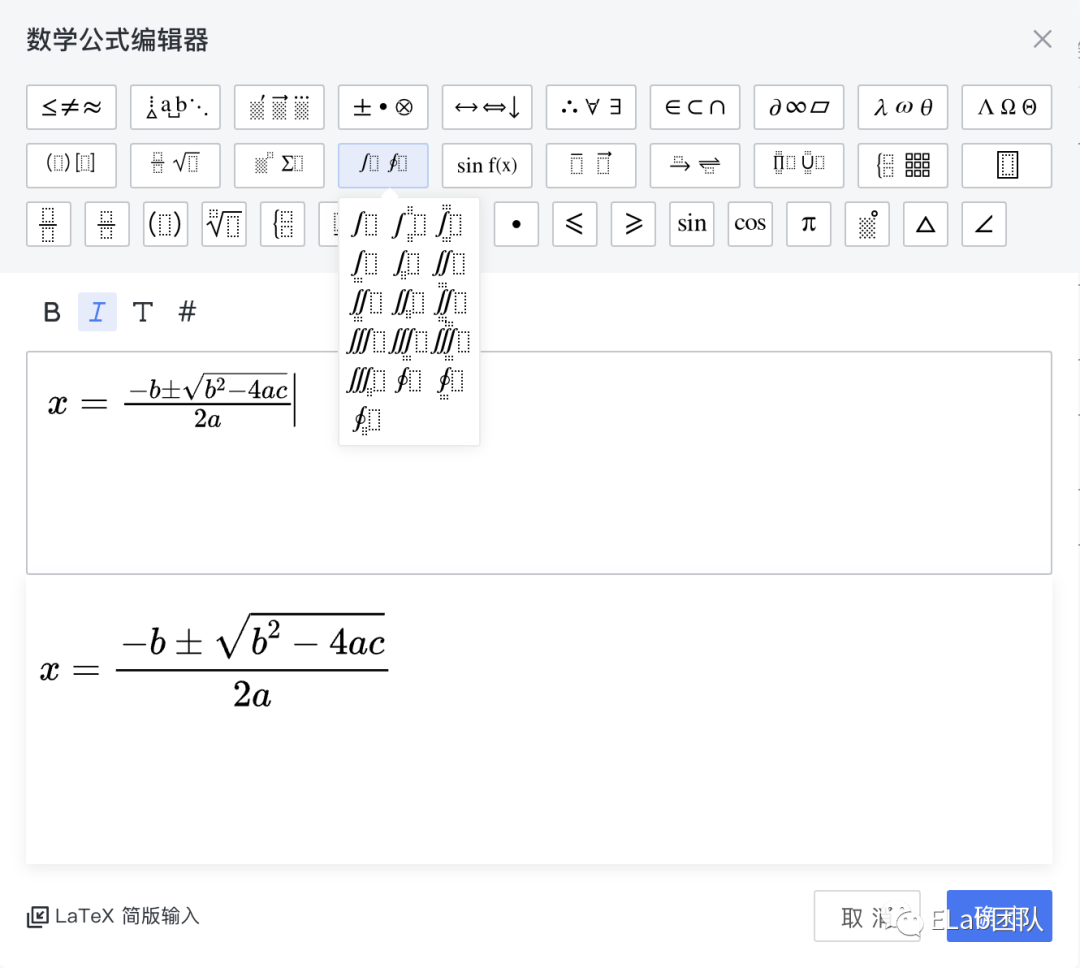
(2)可视化编辑

可视化编辑是将大部分常用元素以可视的形态分组排列展现在工具面板上，用户查找选择，进行公式输入的方式。

公式元素检索

可视检索对于对于不熟悉公式语言的人群来说非常友好，门槛低，开箱即用。但查找慢，且输入元素范围有一定的限制，仅包含工具面板上已提供的公式元素。

大量的可视元素查找目标元素，比较耗时，提高可视元素查找效率是此环节的优化点。

检索结果输入

可视编辑模式下，检索结果为对应的可视元素，点击或回车输入即可，可优化键盘和鼠标的使用比，提高键盘使用率。

5.2.2 关于质量

排除公式含义正确与否，以及对公式有特殊的要求之外，公式质量问题一般出现在产出内容语法不正确。

代码编辑模式下，非常自由，会出现拼写错误，语法错误，误删、误加字符等问题。定位精确、描述准确的错误校验与提示，以及智能的修复或修复建议是重要且友好的质量保障。

可视化编辑模式下，输入元素都需经过严格验证，输入内容需经过严格校验。在此前提下，用户很难生产出有质量问题的公式。

5.3 可能的实现方案

以下列举的解决方案，仅供参考。

5.3.1 代码编辑

公式元素检索

关于此阶段的记忆检索优化，除了用户自行学习之外，编辑器也能提供一定的帮助。编辑器可以将公式面板上的公式语言知识，实时的显示在面板上，增加用户对公式语言知识的了解、以及对编辑器的了解。此处有两个建议：

• 可以通过一张简单的公式拆解图，帮助用户了解公式基础组成要素：符号和结构。

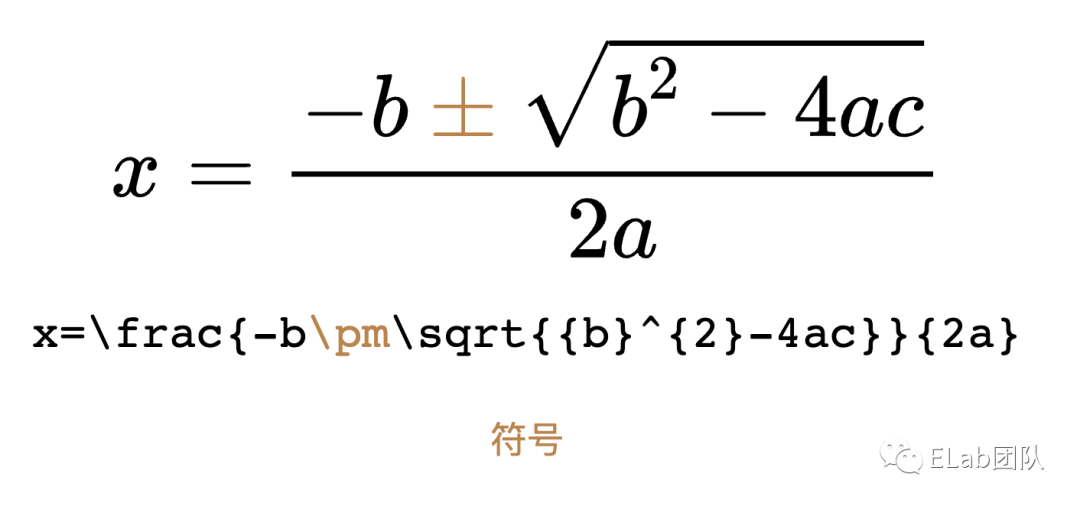
• 鼠标滑过所有的可视化公式元素时，展示对应的公式语言代码，以及简短的解释，增加用户与公式语言知识的接触率，降低用户的记忆成本。

检索结果输入

公式语言作为一门语言，输入元素代码具有相对的固定性，可以通过联想，自动补全，自动识别光标位置，语法高亮等，提升效率。此环节可以参考程序员的代码编辑器。

5.3.2 可视化编辑

公式元素检索

可视化输入元素检索，有以下几点建议：

• 增加可视元素快捷键，解决高频常用元素的检索输入；
• 提供快捷搜索功能，以语言代码、拼音内容，快速检索对应元素；

检索结果输入

键盘输入效率要优于鼠标输入，设计上可以尽可能提高键盘的覆盖率，提高键盘操作的连贯性。

5.3.3 弱化代码编辑和可视编辑的边界

在人群中，对公式语言的各种熟练程度都会有。公式语言相对不熟悉的人群可能更习惯使用可视化编辑，某些情况下也需要借助源码编辑，解决面板元素覆盖不全等问题；公式语言相对熟悉的人群可能更习惯使用源码编辑模式，但也免不了，有些代码记不住，需要通过可视面板输入的情况。

所以可视化模式提供公式语言代码输入能力，以及代码模式提供可视化元素输入能力，等弱化两者边界，会是一个较好的优化方向。

5.3.4 定向优化

在实际情况中，公式编辑器可能具备特定的条件，如化学学科公式录入，如小学公式录入。这种情况可以根据特定的场景，设计特定的优化策略。如化学学科，因为化学公式具备一定的特征，可以提供针对这些特征的快捷输入，比如H2O表达等；如小学学端公式录入，可以预先收集小学公式库，提供输入联想补全能力。