DOM diff 原理详解

DOM diff 作为工程问题，需要具有一定算法思维，因此经常出现在面试场景中，毕竟这是难得出现在工程领域的算法问题。

无论出于面试目的，还是深入学习目的，都有必要将这个问题搞懂，因此前端精读我们就专门用一个章节说清楚此问题。

精读

Dom diff 是所有现在框架必须做的事情，这背后的原因是，由 Jquery 时代的面向操作过程转变为数据驱动视图导致的。

为什么 Jquery 时代不需要 Dom diff？因为 Dom diff 交给业务处理了，我们调用 .append 或者 .move 之类 Dom 操作函数，就是显式申明了如何做 Dom diff，这种方案是最高效的，因为怎么移动 Dom 只有业务最清楚。

但这样的问题也很明显，就是业务心智负担太重，对于复杂系统，需要做 Dom diff 的地方太多，不仅写起来繁琐，当状态存在交错时，面向过程的手动 Dom diff 容易出现状态遗漏，导致边界错误，就算你没有写出 bug，代码的可维护性也绝对算不上好。

解决方案就是数据驱动，我们只需要关注数据如何映射到 UI，这样无论业务逻辑再复杂，我们永远只需要解决局部状态的映射，这极大降低了复杂系统的维护复杂度，以前需要一个老手写的逻辑，现在新手就能做了，这是非常了不起的变化。

但有利也有弊，这背后 Dom diff 就要交给框架来做了，所以是否能高效的做 Dom diff，是一个数据驱动框架能否应用于生产环境的重要指标，接下来，我们来看看 Dom diff 是如何做的吧。

理想的 Dom diff

如图所示，理想的 Dom diff 自然是滴水不漏的复用所有能复用的，实在遇到新增或删除时，才执行插入或删除。这样的操作最贴近 Jquery 时代我们手写的 Dom diff 性能。

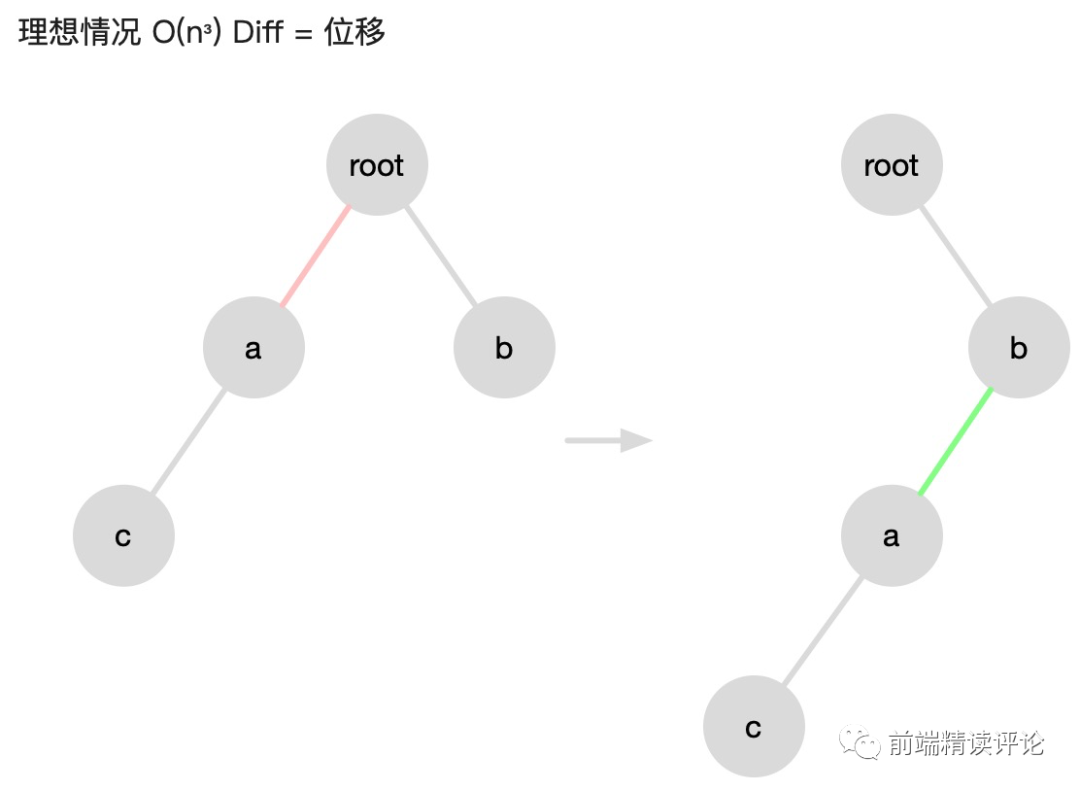
可惜程序无法猜到你的想法，想要精确复用就必须付出高昂的代价：时间复杂度 O(n³) 的 diff 算法，这显然是无法接受的，因此理想的 Dom diff 算法无法被使用。

关于 O(n³) 的由来。由于左树中任意节点都可能出现在右树，所以必须在对左树深度遍历的同时，对右树进行深度遍历，找到每个节点的对应关系，这里的时间复杂度是 O(n²)，之后需要对树的各节点进行增删移的操作，这个过程简单可以理解为加了一层遍历循环，因此再乘一个 n。

简化的 Dom diff

如图所示，只按层比较，就可以将时间复杂度降低为 O(n)。按层比较也不是广度遍历，其实就是判断某个节点的子元素间 diff，跨父节点的兄弟节点也不必比较。

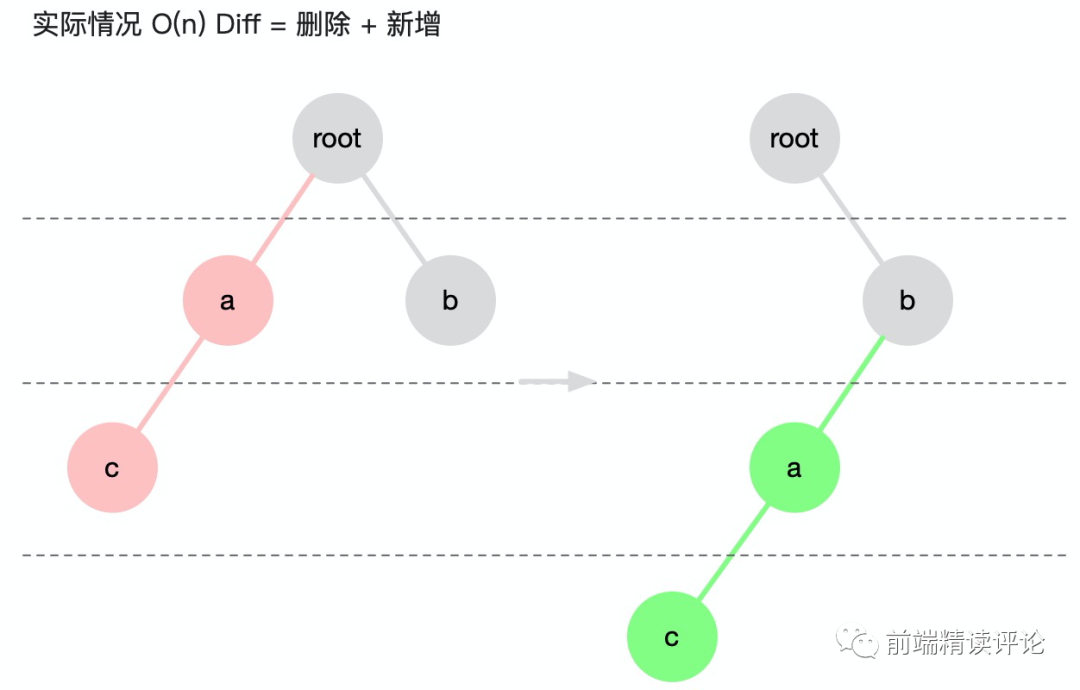
这样做确实非常高效，但代价就是，判断的有点傻，比如 ac 明明是一个移动操作，却被误识别为删除 + 新增。

好在跨 DOM 复用在实际业务场景中很少出现，因此这种笨拙出现的频率实际上非常低，这时候我们就不要太追求学术思维上的严谨了，毕竟框架是给实际项目用的，实际项目中很少出现的场景，算法是可以不考虑的。

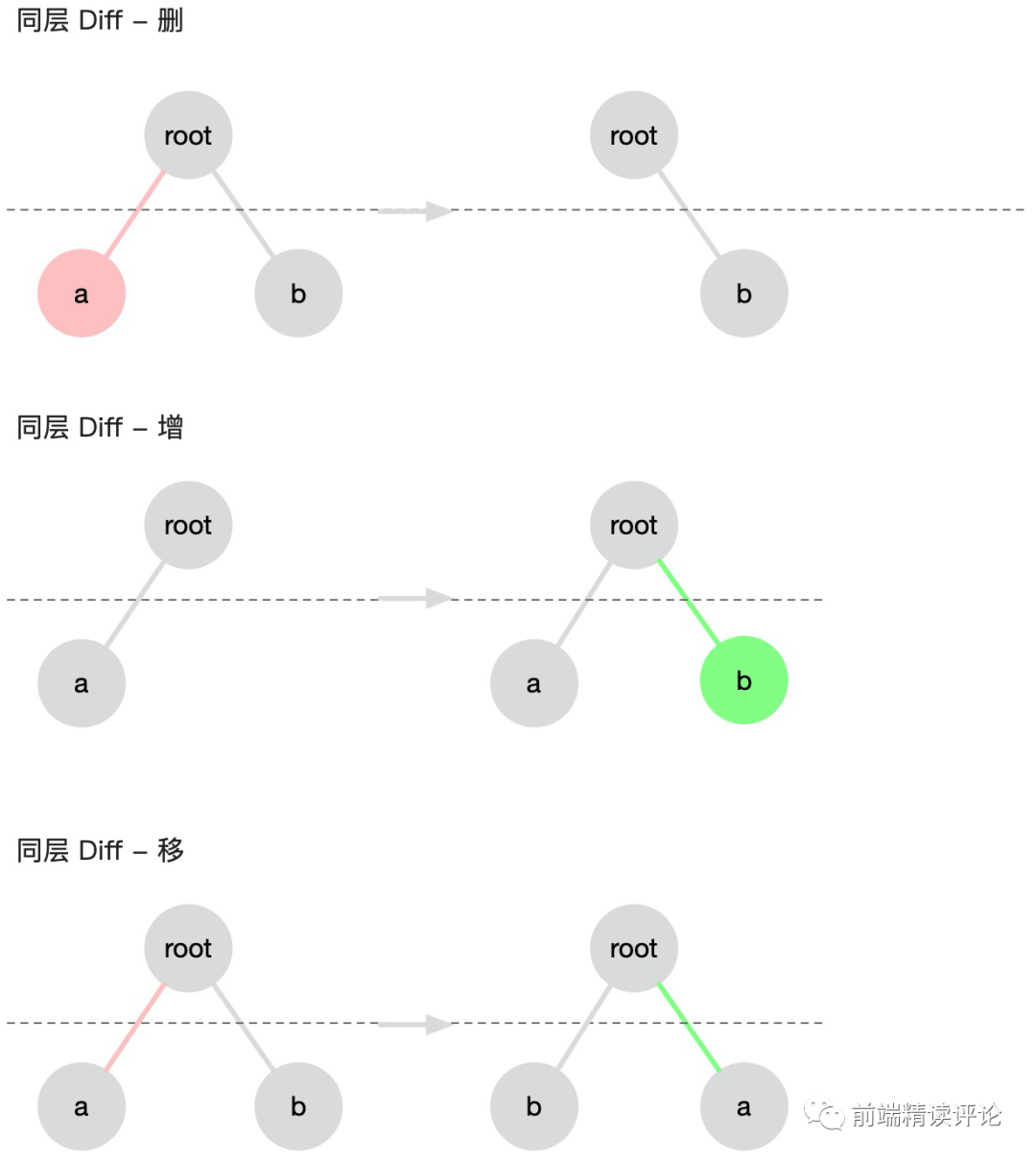
下面是同层 diff 可能出现的三种情况，非常简单，看图即可：

那么同层比较是怎么达到 O(n) 时间复杂度的呢？我们来看具体框架的思路。

Vue 的 Dom diff

Vue 的 Dom diff 一共 5 步，我们结合下图先看前三步：

如图所示，第一和第二步分别从首尾两头向中间逼近，尽可能跳过首位相同的元素，因为我们的目的是 尽量保证不要发生 dom 位移。

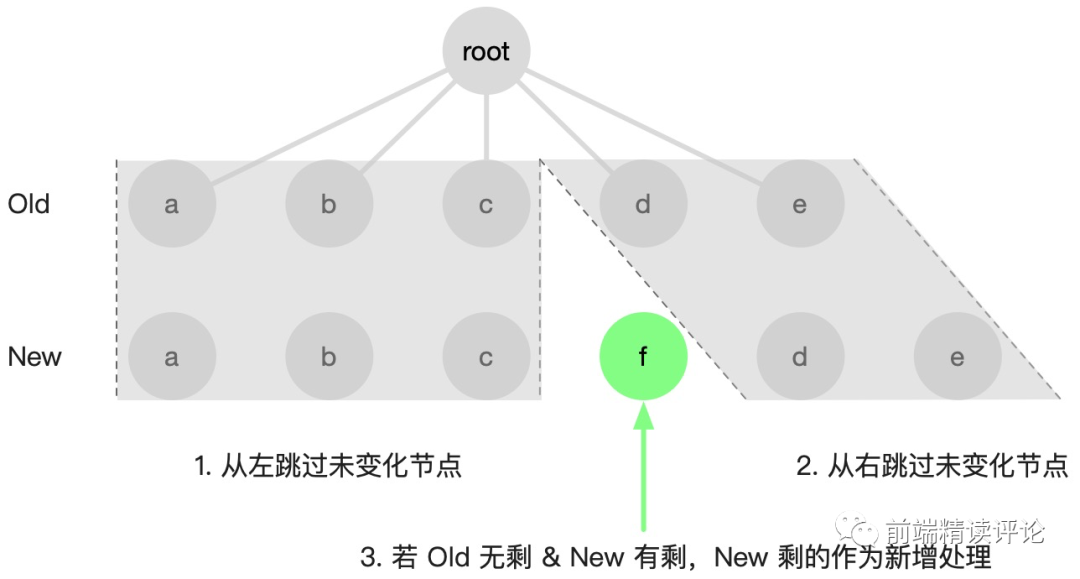
这种算法一般采用双指针。如果前两步做完后，发现旧树指针重合了，新树还未重合，说明什么？说明新树剩下来的都是要新增的节点，批量插入即可。很简单吧？那如果反过来呢？如下图所示：

第一和第二步完成后，发现新树指针重合了，但旧树还未重合，说明什么？说明旧树剩下来的在新树都不存在了，批量删除即可。

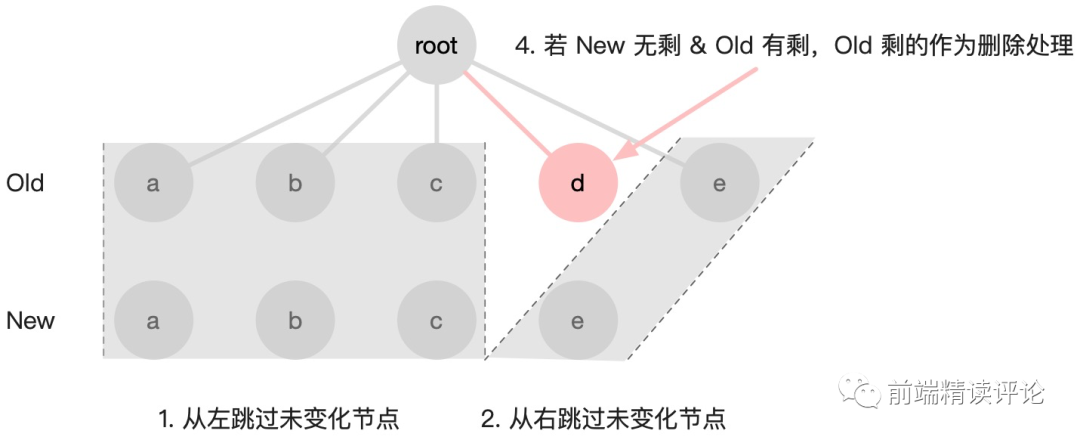
当然，如果 1、2、3、4 步走完之后，指针还未处理完，那么就进入一个小小算法时间了，我们需要在 O(n) 时间复杂度内把剩下节点处理完。熟悉算法的同学应该很快能反映出，一个数组做一些检测操作，还得把时间复杂度控制在 O(n)，得用一个 Map 空间换一下时间，实际上也是如此，我们看下图具体做法：

如图所示，1、2、3、4 步走完后，Old 和 New 都有剩余，因此走到第五步，第五步分为三小步：

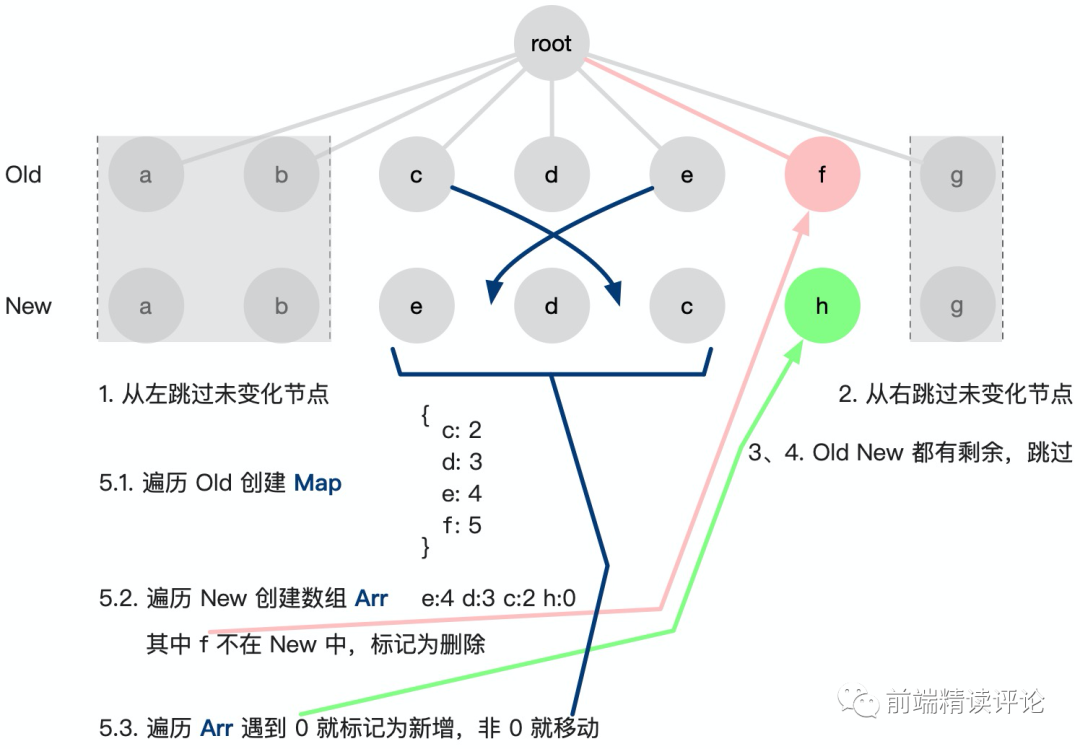
1. 遍历 Old 创建一个 Map，这个就是那个换时间的空间消耗，它记录了每个旧节点的 index 下标，一会好在 New 里查出来。
2. 遍历 New，顺便利用上面的 Map 记录下下标，同时 Old 里不存在的说明被删除了，直接删除。
3. 不存在的位置补 0，我们拿到 e:4 d:3 c:2 h:0 这样一个数组，下标 0 是新增，非 0 就是移过来的，批量转化为插入操作即可。

最后一步的优化也很关键，我们不要看见不同就随便移动，为了性能最优，要保证移动次数尽可能的少，那么怎么才能尽可能的少移动呢？假设我们随意移动，如下图所示：

但其实最优的移动方式是下面这样：

为什么呢？因为移动的时候，其他元素的位置也在相对变化，可能做了 A 效果同时，也把 B 效果给满足了，也就是说，找到那些相对位置有序的元素保持不变，让那些位置明显错误的元素挪动即是最优的。

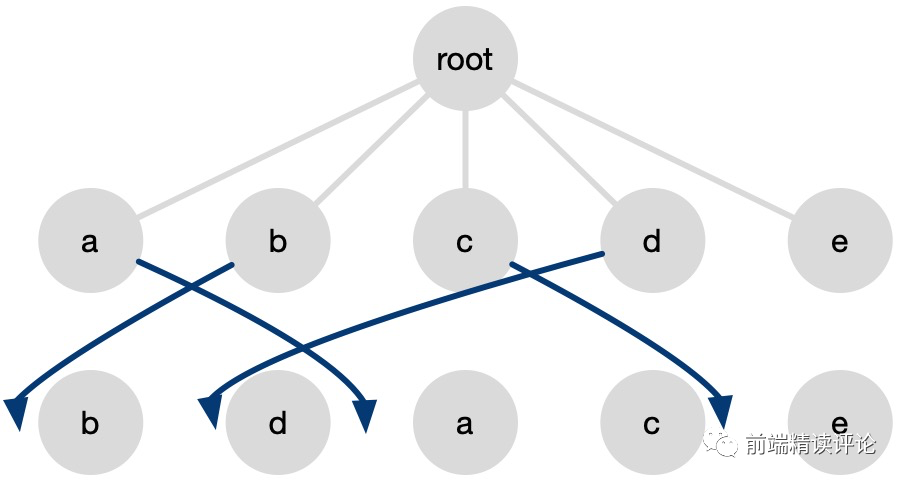
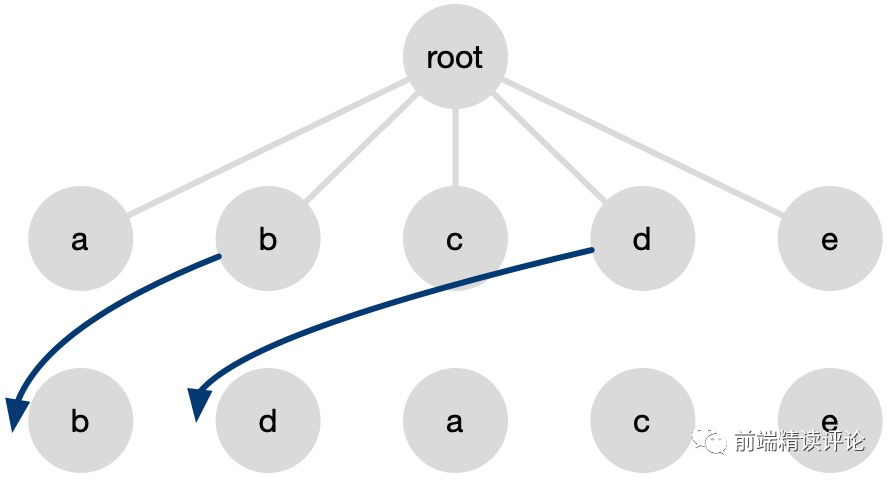
什么是相对有序？a c e 这三个字母在 Old 原始顺序 a b c d e 中是相对有序的，我们只要把 b d 移走，这三个字母的位置自然就正确了。因此我们只需要找到 New 数组中的 最长连续子串。具体的找法可以当作一个小算法题了，由于知道每个元素的实际下标，比如这个例子中，下标是这样的：

[b:1, d:3, a:0, c:2, e:4]

肉眼看上去，连续自增的子串有 b d 和 a c e，由于 a c e 更长，所以选择后者。

换成程序去做，可以采用动态规划，设 dp(i) 为以第 i 个字符串结尾的最长连续子串长度，一次 O(n) 循环即可。

// dp(i) = num[i] > num[i - 1] ? dp(i - 1) + 1 : 1

React 的 Dom diff

假设这么一种情况，我们将 a 移到了 c 后，那么框架从最终状态倒推，如何最快的找到这个动机呢？React 采用了 仅右移策略，即对元素发生的位置变化，只会将其移动到右边，那么右边移完了，其他位置也就有序了。

我们看图说明：

遍历 Old 存储 Map 和 Vue 是一样的，然后就到了第二步遍历 New，b 下标从原来的 1 变成了 0，需要左移才行，但我们不左移，我们只右移，因为所有右移做完后，左移就等于自动做掉了（前面的元素右移后，自己自然被顶到前面去了，实现了左移的效果）。

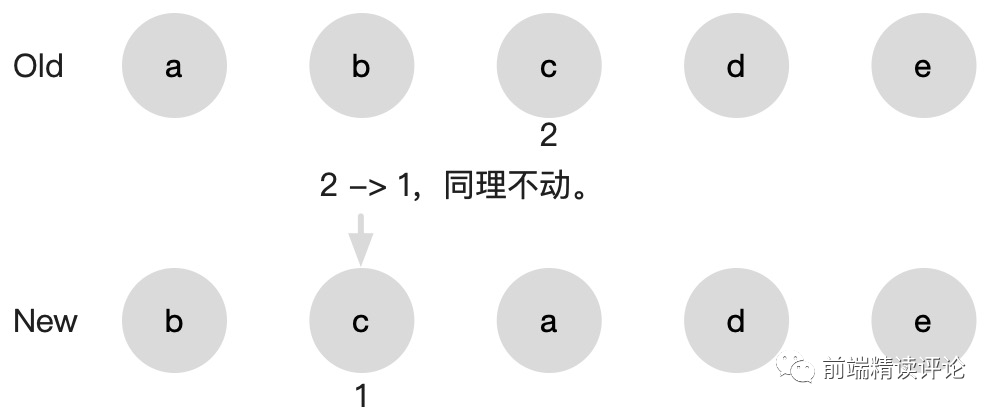
同理，c 下标从 2 变成了 1，需要左移才行，但我们继续不动。

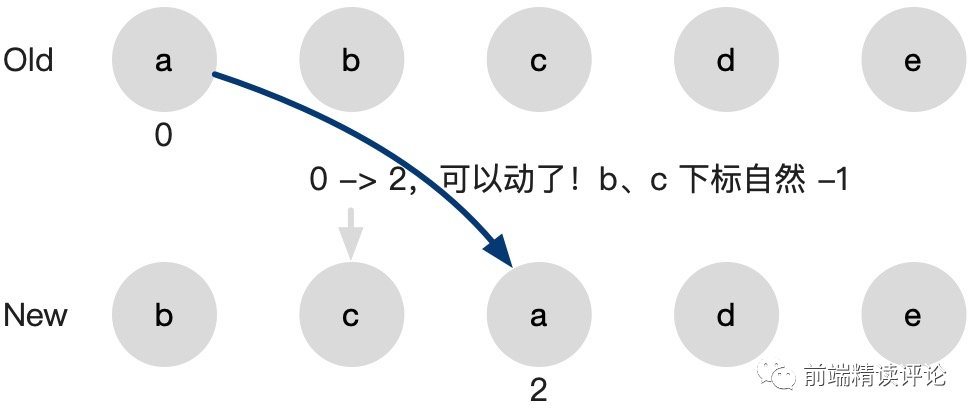
a 的下标从 0 变成 2，终于可以右移了！

后面的 d、e 下标没变，就不用动。我们纵观整体可以发现，b 和 c 因为前面的 a 被抽走了，自然发生了左移。这就是用一个右移代替两个左移的高效操作。

同时我们发现，这也确实找到了我们开始提到的最佳位移策略。

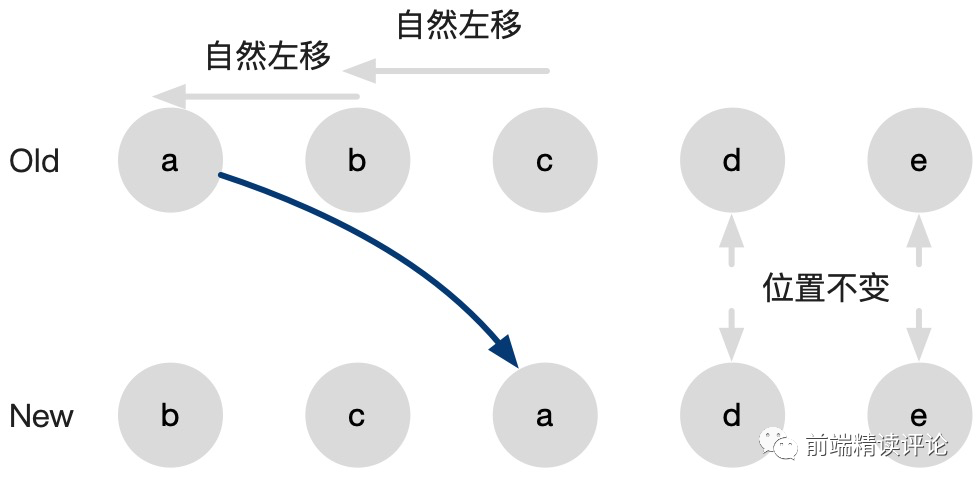
那这个算法真的有这么聪明吗？显然不是，这个算法只是歪打误撞碰对了而已，有用右移替代左移的算法，就有用左移替代右移的算法，既然选择了右移替代左移，那么一定丢失了左移代替右移的效率。

什么时候用左移代替右移效率最高？就是把数组最后一位移到第一位的场景：

显然左移只要一步，那么右移就是 n-1 步，在这个例子就是 4 步，我们看右移算法图解：

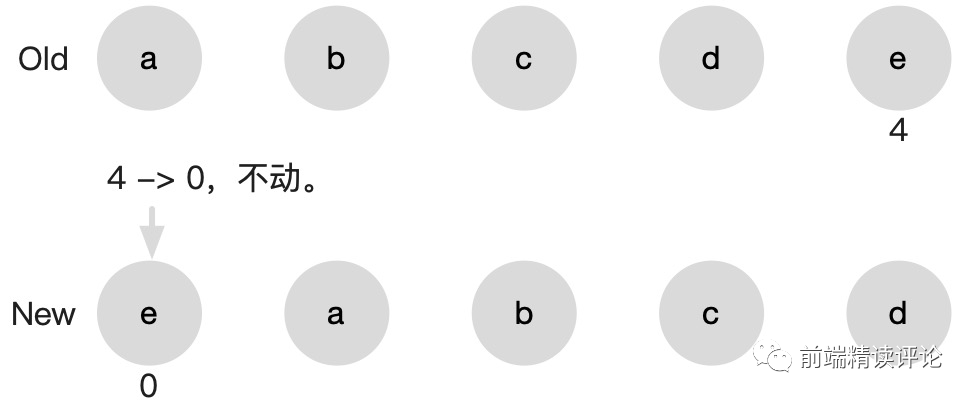
首先找到 e，位置从 4 变成了 0，但我们不能左移！所以只能保持不动，悲剧从此开始。

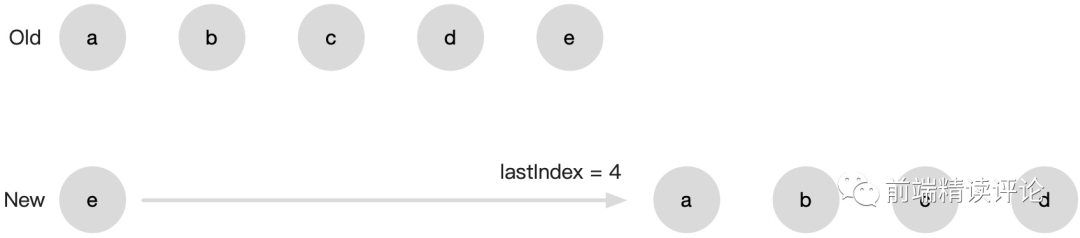
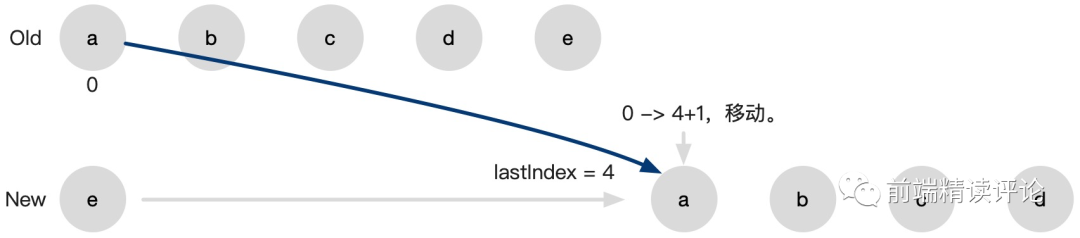
虽然算法已经不是最优了，但该做的还是要做，其实之前有一个 lastIndex 概念没有说，因为 e 已经在 4 的位置了，所以再把 a 从 0 挪到 1 已经不够了，此时 a 应该从 0 挪到 5。

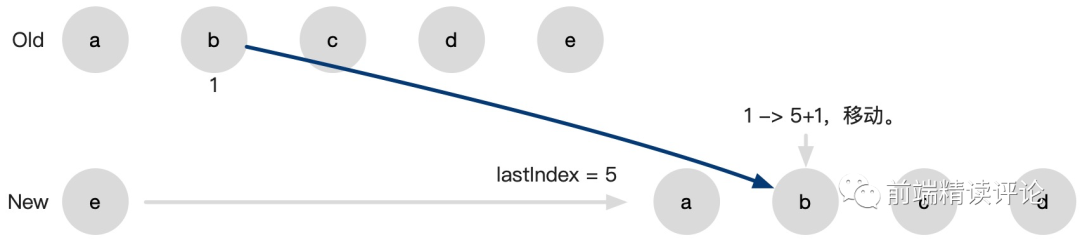
方法就是记录 lastIndex = max(oldIndex, newIndex) => lastIndex = max(4, 0)，下一次移动到 lastIndex + 1 也就是 5：

发现 a 从 0 变成了 5（注意，此时考虑到 lastIndex 因素），所以右移。

同理，b、c、d 也一样。我们最后发现，发生了 4 次右移，e 也因为自然左移了 4 次到达了首位，符合预期。

所以这是一个有利有弊的算法。新增和删除比较简单，和 Vue 差不多。

PS：最新版 React Dom diff 算法如有更新，欢迎在评论区指出，因为这种算法看来不如 Vue 的高效。

总结

Dom diff 总结有这么几点考虑：

1. 完全对比 O(n³) 无法接受，故降级为同层对比的 O(n) 方案。
2. 为什么降级可行？因为跨层级很少发生，可以忽略。
3. 同层级也不简单，难点是如何高效位移，即最小步数完成位移。
4. Vue 为了尽量不移动，先左右夹击跳过不变的，再找到最长连续子串保持不动，移动其他元素。
5. React 采用仅右移方案，在大部分从左往右移的业务场景中，得到了较好的性能。