数据结构与算法篇-队列实现栈

01

队列实现栈原理简述

栈是一种后进先出的数据结构，而队列是一种先进先出的数据结构，两者原理不难理解，使用也简单。但是我们不仅仅要掌握数据结构的基本原理，还要学会灵活运用，能否灵活运用是考察一个人对数据结构的理解程度，也是在面试的时候经常会考到的知识点。现在假设面试官要求你用队列实现栈，你的解决方案是什么？通过栈的基本原理我们知道，只要每次进行stack_pop操作时将队列里最后一个元素输出就能模拟栈的输出操作。

02

队列实现栈方案和实现

方案1：

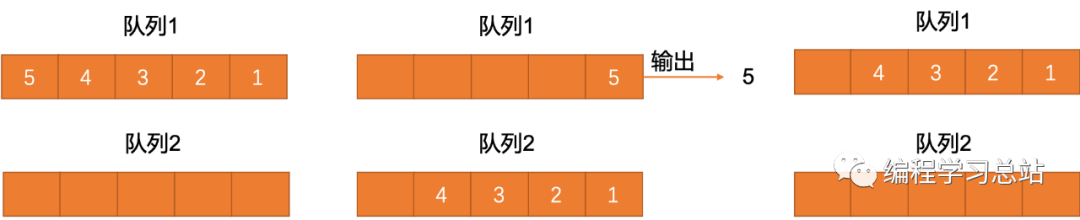
我们很容易想到一种解决方案，队列queue1保存原始输入数据，队列queue2作为临时队列缓存数据，只要进行stack_pop操作时，先将queue1里除最后一个元素外全部出队，且出队的数据保存在一个临时队列queue2里，保存queue1最后的元素，最后再将queue2里的全部元素出队，且出队的元素重新放进queue1里，返回保存的queue1最后的元素。

我们作了下图便于理解2个队列模拟栈的过程。

一个栈输出元素顺序

两个队列queue1和queue2模拟栈

在数据结构与算法篇-队列和数据结构与算法篇-栈文章里我们详细介绍了队列和栈的原理，并都用C实现了队列和栈。现在我们复用这两篇文章里队列的实现代码，用于实现栈。定义栈相关数据结构和操作函数代码如下：

typedef struct stack{
    queue_arr_t queue1;
    queue_arr_t queue2;
}_stack_t;
extern void stack_init(_stack_t *s, int cap);
extern void stack_destroy(_stack_t *s);
extern void stack_push(_stack_t *s, int data);
extern int stack_pop(_stack_t *);
extern int stack_pop2(_stack_t *s);
extern bool stack_is_empty(_stack_t *s);
extern bool stack_is_full(_stack_t *s);

栈初始化函数实现：

void stack_init(_stack_t *s, int cap){
    if(s == NULL || cap <= 0){
        return;
    }

    queue_arr_init(&s->queue1, cap);
    queue_arr_init(&s->queue2, cap);
}

栈销毁函数实现：

void stack_destroy(_stack_t *s){
    if(s == NULL){
        return;
    }
    queue_arr_destroy(&s->queue1);
    queue_arr_destroy(&s->queue2);
}

入栈函数实现：

void stack_push(_stack_t *s, int data){
    if(s == NULL){
        return;
    }
    enqueue_arr(&s->queue1, data);
}

出栈函数实现：

int stack_pop(_stack_t *s){
    if(s == NULL){
        return NAN;
    }
    if(queue_arr_is_empty(&s->queue1)){
        return NAN;
    }

    while(queue_arr_length(&s->queue1) > 1){
        enqueue_arr(&s->queue2, dequeue_arr(&s->queue1));
    }
    int data = dequeue_arr(&s->queue1);
    while(!queue_arr_is_empty(&s->queue2)){
        enqueue_arr(&s->queue1, dequeue_arr(&s->queue2));
    }
    return data;
}

判断栈是否空和是否满函数实现：

bool stack_is_empty(_stack_t *s){
    if(s == NULL){
        return true;
    }
    return queue_arr_is_empty(&s->queue1);
}

bool stack_is_full(_stack_t *s){
    if(s == NULL){
        return false;
    }
    return queue_arr_is_full(&s->queue1);
}

从方案1我们知道每次出队都需要将队列里除最后一个元素外的元素保存在另外一个临时队列里，增加了空间复杂度。那么能否只用一个队列能否模拟栈呢？通过仔细观察方案1发现queue1出对的数据是可以重新再入队的，只要让队列里最后一个元素在队列头即可，那么我们很容易想到方案2。

方案2： 将队列queue1里的数据依次出队，且出队的数据重新放在queue1的队尾，直到最后一个元素在队列头，最后输出队列头的元素即可。整个过程我们可以用下图表示。 单个队列模拟栈

单个队列模拟出栈函数实现如下：

int stack_pop2(_stack_t *s){
    if(s == NULL){
        return NAN;
    }
    if(queue_arr_is_empty(&s->queue1)){
        return NAN;
    }
    int length = queue_arr_length(&s->queue1) - 1;
    int data;
    while(length--){
        data = dequeue_arr(&s->queue1);
        enqueue_arr(&s->queue1, data);
    }
    return dequeue_arr(&s->queue1);
}

03

栈实现验证

下面我们写一个小程序验栈实现的正确性。

#include <stdio.h>
#include "stack.h"

int main() {
    int i = 0;
    _stack_t my_stack;

    stack_init(&my_stack, 5);
    printf("入栈顺序\n");
    for(i = 0; i < 5; i++){
        printf("%d ", i + 1);
        stack_push(&my_stack, i + 1);
    }
    printf("\n");
    printf("出栈顺序\n");
    for(i = 0; i < 5; i++){
        printf("%d ", stack_pop(&my_stack));
    }
    printf("\n\n");
    printf("优化出栈操作\n");
    printf("入栈顺序\n");
    for(i = 0; i < 5; i++){
        printf("%d ", i + 1);
        stack_push(&my_stack, i + 1);
    }
    printf("\n");
    printf("出栈顺序\n");
    for(i = 0; i < 5; i++){
        printf("%d ", stack_pop2(&my_stack));
    }
    printf("\n");

    stack_destroy(&my_stack);

    return 0;
}

编译运行输出如下：

入栈顺序
1 2 3 4 5 
出栈顺序
5 4 3 2 1 

优化出栈操作
入栈顺序
1 2 3 4 5 
出栈顺序
5 4 3 2 1

队列模拟栈完全正确。