01

—

认识堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，它的最好、最好、平均复杂度都为nlog(n)，它也是不稳定排序算法。

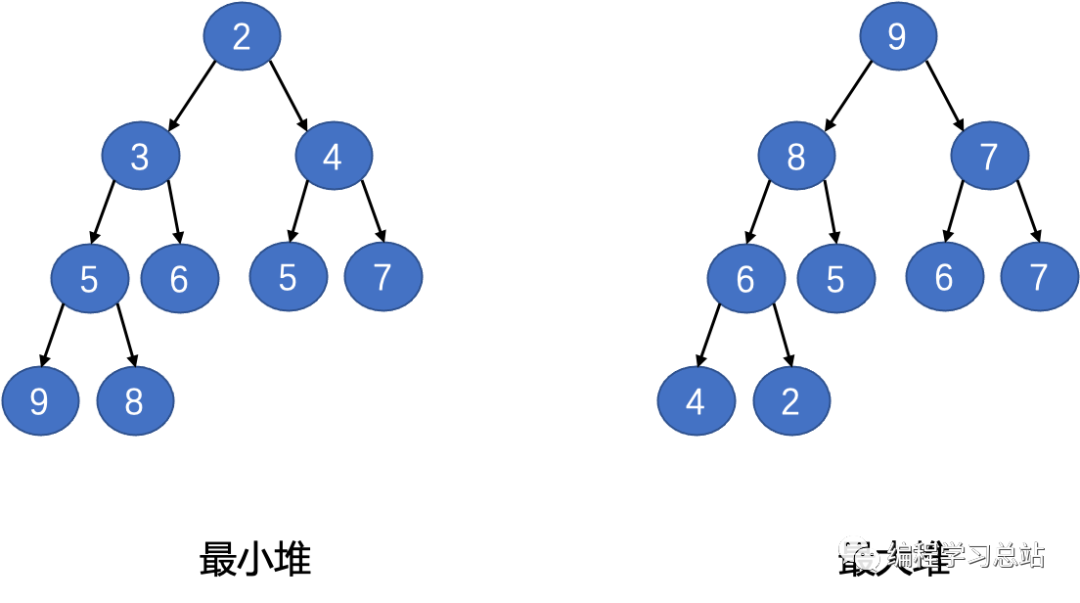
堆是具有以下性质的完全二叉树：每个结点的值都大于等于其左右孩子结点的值，称为最大堆。每个结点的值都小于等于其左右孩子结点的值，称为最小堆。如下图：

02

—

堆排序思想及其实现

无论网上还是书本上介绍堆排序的实现都是用数组实现，但是今天我们用二叉树的思想实现堆排序。

堆排序思想：将待排序列构造成一个最小堆，此时整个序列的最小值就是堆的根结点，新结点插入都将从左子树开始填充到右子树，新插入的结点先成为叶子结点，再从新插入的结点开始往上遍历，如果父结点的值比该结点的值大则交换数据，直到父结点的值比其结点的值小为止。重复对n个值进行操作，依次取出根结点，则整个序列是有序的。定义堆结点和声明操作函数：

#define INT_NAN (0xFFFFFFFF - 1)

typedef struct tree_node{
    struct tree_node *left;
    struct tree_node *right;
    int data;
    int height;
}tree_node_t;
extern tree_node_t *new_tree_node(int data);
extern int heap_sort_get_node(tree_node_t **root);
extern void heap_sort_insert_node(tree_node_t **root, int data);
extern void destroy_heap_tree(tree_node_t *root);
extern void tree_print(tree_node_t *root);

堆结点里的高度并不是二叉树的高度，由于二叉堆是完全二叉树，因此只要结点的左右子树不是满二叉树且高度不一致时，就可继续插入结点，直到左右子树都是满二叉树且高度一致，再往下一层插入结点。

新建堆结点函数实现：

tree_node_t *new_tree_node(int data){
    tree_node_t *node = malloc(sizeof(tree_node_t));
    if(node == NULL){
        return NULL;
    }
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    node->height = 1;

    return node;
}

释放堆结点函数实现：

if(node == NULL){
        return;
    }
    node->left = NULL;
    node->right = NULL;
    free(node);
}

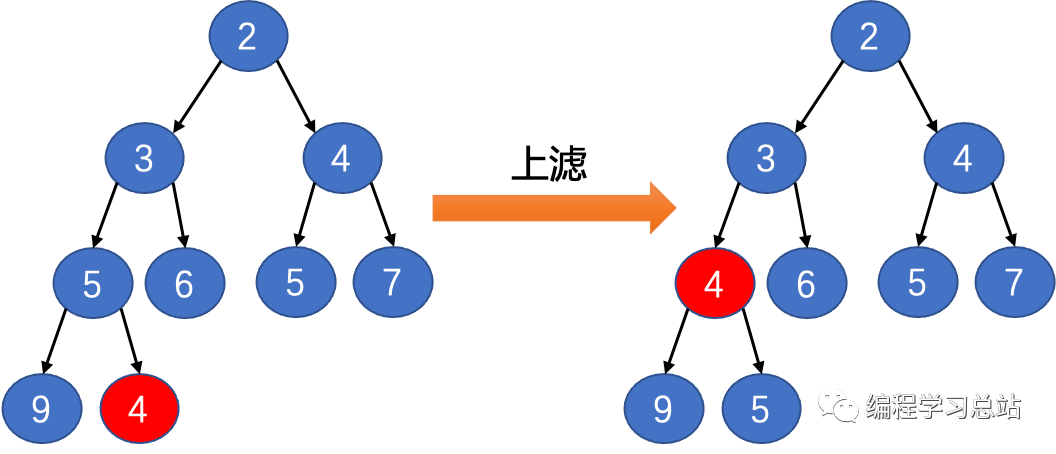
二叉堆插入结点步骤：将新插入的结点按照层级结构成为叶子结点，再从新结点往根结点遍历，如果其父结点的值比该结点的值小，则交换数据，这个过程称为上滤。新插入的结点不断上滤，直到父结点的值比其结点的值小则停止上滤。如图所示：

交换数据函数实现：

void swap(int *a, int *b){
    int c = *a;
    *a = *b;
    *b = c;
}

上滤操作函数实现：

tree_node_t *up_filter(tree_node_t *root){
    if(root == NULL){
        return NULL;
    }
    if(root->left != NULL && root->right != NULL){
        if(root->data > root->left->data){
            swap(&root->data, &root->left->data);
        }
        if(root->data > root->right->data){
            swap(&root->data, &root->right->data);
        }
    }else if(root->left != NULL){
        if(root->data > root->left->data){
            swap(&root->data, &root->left->data);
        }
    }else if(root->right != NULL){
        if(root->data > root->right->data){
            swap(&root->data, &root->right->data);
        }
    }
    return root;
}

插入堆结点函数实现：

int get_balance_factor(tree_node_t *root){
    if(root->left != NULL && root->right != NULL){
        return root->left->height - root->right->height;
    }else if(root->left != NULL && root->right == NULL){
        return root->left->height;
    }else if(root->left == NULL && root->right != NULL){
        return 0 - root->right->height;
    }
    return 0;
}

tree_node_t *sub_tree_insert_node(tree_node_t *root, int data){
    if(root == NULL){
        return new_tree_node(data);
    }
    int factor = get_balance_factor(root);
    if(factor <= 0){
        //插入左边
        //printf("to left\n");
        root->left = sub_tree_insert_node(root->left, data);
    }else{
        //插入右边
        //printf("to right\n");
        root->right = sub_tree_insert_node(root->right, data);
    }
    //printf("current node: %d\n", root->data);
    return up_filter(root);
}

void update_height(tree_node_t *root){
    if(root == NULL){
        return;
    }
    update_height(root->left);
    update_height(root->right);
    if(root->left != NULL && root->right != NULL){
        root->height = root->left->height < root->right->height ? root->left->height : root->right->height;
        root->height++;
    }else{
        root->height = 1;
    }
}

void heap_sort_insert_node(tree_node_t **root, int data){
    if(root == NULL){
        return;
    }
    *root = sub_tree_insert_node(*root, data);
    update_height(*root);
}

插入结点使用递归实现，每次插入结点后都要更新堆结点里面的height属性，每个非根结点的height属性由左右子树决定。二叉堆也是二叉树，根据二叉树的几种遍历方式我们知道，通过后续遍历便可调整每个结点的height属性。而update_height函数便可调整二叉堆所有结点的height属性。获取结点函数实现：

tree_node_t *add_sub_tree_to_tree(tree_node_t *root, tree_node_t *sub){
    if(sub == NULL || root == NULL){
        return root;
    }
    add_sub_tree_to_tree(root, sub->left);
    add_sub_tree_to_tree(root, sub->right);
    return sub_tree_insert_node(root, sub->data);
}

int heap_sort_get_node(tree_node_t **root){
    if(root == NULL || *root == NULL){
        return INT_NAN;
    }
    tree_node_t *tree_root = *root;
    int data = tree_root->data;
    //printf("first node: %d\n", tree_root->data);
    if(tree_root->left == NULL && tree_root->right == NULL){
        free_tree_node(tree_root);
        *root = NULL;
    }else if(tree_root->left == NULL && tree_root->right != NULL){
        //右孩子非空，右孩子代替原结点
        *root = tree_root->right;
        free_tree_node(tree_root);
    }else if(tree_root->right == NULL && tree_root->left != NULL){
        //左孩子非空，左孩子代替原结点
        *root = tree_root->left;
        free_tree_node(tree_root);
    }else{
        //左右孩子非空
        tree_node_t *temp = NULL;
        tree_node_t *free_node = tree_root;
        if(tree_root->left->data < tree_root->right->data){
            //左孩子小于右孩子，左孩子代替原结点
            temp = tree_root->left->right;
            tree_root->left->right = tree_root->right;
            *root = tree_root->left;
        }else{
            //右孩子小于左孩子，右孩子代替原结点
            temp = tree_root->right->left;
            tree_root->right->left = tree_root->left;
            *root = tree_root->right;
        }
        free_tree_node(free_node);
        *root = add_sub_tree_to_tree(*root, temp);
        destroy_heap_tree(temp);
    }
    return data;
}

void destroy_heap_tree(tree_node_t *root){
    if(root == NULL){
        return;
    }
    destroy_heap_tree(root->left);
    destroy_heap_tree(root->right);
    free_tree_node(root);
}

和二叉搜索树不同的是，每删除一个结点都要维护最小堆的性质。被删除的结点要从左右子树根结点里选择较小值的结点代替原结点。这里我们要考虑几种情况：

1、被删除结点没有左右子树：直接删除即可。

2、被删除结点只有左子树：用左子树根结点代替原结点。

3、被删除结点只有右子树：用右子树根结点代替原结点。

4、被删除结点有左右子树：左右子树根结点较小值的结点代替原结点，如图所示：

03

—

算法验证

我们写个小程序验证堆排序算法的正确性：

#include <stdio.h>
#include "heap_sort.h"

int main()
{
    int arr[8] = {8, 2, 9, 1, 6, 9, 0, 4};
    int i = 0;
    tree_node_t *root = NULL;

    printf("输入原始序列\n");
    for(i = 0; i < 8; i++){
        printf("%d, ", arr[i]);
        heap_sort_insert_node(&root, arr[i]);
    }
    printf("\n");
    printf("最小堆输出\n");
    for(i = 0; i < 8; i++){
        printf("%d, ", heap_sort_get_node(&root));
    }
    printf("\n");

    return 0;
}

编译输出如下：

输入原始序列
8, 2, 9, 1, 6, 9, 0, 4, 
最小堆输出
0, 1, 2, 4, 6, 8, 9, 9,

堆排序算法完全正确！