浅谈图的层次布局
简介
图是一种常见的数据结构和表示形式,可视化场景也经常会用到图来展现有关联关系的数据。进行图的可视化时,往往需要将其自动布局,而针对不同的问题和场景,需要不同的布局方法。本文主要介绍图的层次布局的思路。

图的层次布局
在数据有一定层级结构或先后顺序时,经常会用到层次布局来展现,一般对应的数据结构是DAG(Directed Acyclic Graph,即有向无环图)。常用的场景包括:流程图、组织架构图、状态转移图等。
层次布局[2]的方法是 Kozo Sugiyama 首先于1981年详细阐明的,因此也常被称为 Sugiyama 布局。这里我们讲一下Sugiyama布局的思路。
目的
根据图的数据,自动画出一个易于理解的有层次(hierarchy)的图。
-
节点的布局是有层次的 - Hierarchical
-
边的交叉尽可能的少 - Less Crossing
-
边的路径尽量可以是一条直线 - Straight
-
边的路径尽可能的短 - Close
-
布局尽可能平衡 - Balanced
画图的基本规则
- 如何放置节点 - 每一层的节点都放在同一水平线上,且不重叠
- 如何画边 - 每条边都通过直线画出
这样,给节点分层后,把每层的节点放到合理的水平位置,就可以把图画出来。
布局思路
根据以上原则,Sugiyama把图的布局问题分成了多个步骤,每个步骤解决不同的子问题。Sugiyama算法总共分为以下4步。
步骤1:节点分层
-
根据边的方向,把节点划分到不同层
-
如果有边跨越了多层,在穿过的每一层增加一个伪节点与其相连,保证每条边只连接相邻的两层
-
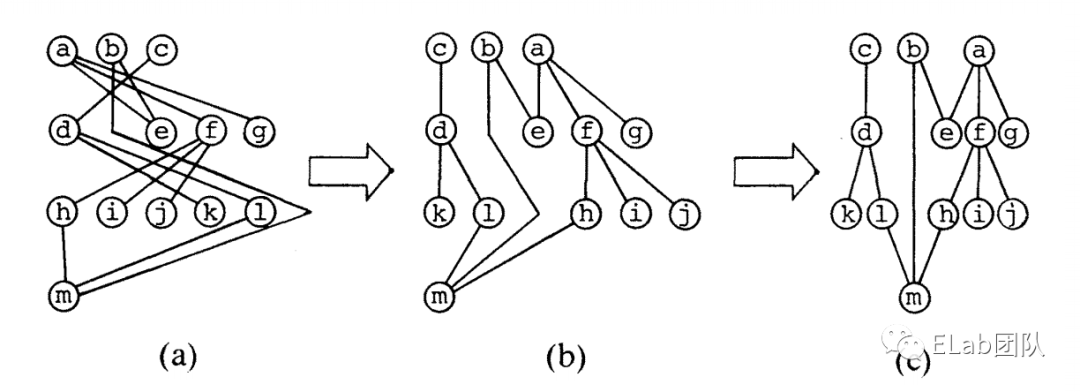
如图(a)
步骤2:减少交叉
- 改变每层的节点的顺序来减少边的交叉
- 如图 (a) -> (b)
步骤3:计算节点坐标
- 在保证上一步的节点顺序的基础上,调整节点的水平位置来满足上述Straight、Close、Balanced原则
- 如图 (b) -> (c)
步骤4:画图
- 根据之前步骤生成的节点位置把图画出来,并移除伪节点和边。
- 如图(c)
每一步的具体算法
看起来是很简单的4步,但每一步的实现都并不简单,也有很多种不同的算法。
节点分层
怎么把节点分到不同的层呢?这里介绍几种算法。
- 最长路径算法(Longest Path)
首先最容易想到的可能就是最长路径算法。即一个节点的层级等于要到达它需要走过的最长路径。最长路径算法的优点是速度很快,遍历图即可完成分层。然而它有比较明显的问题:节点被分到尽可能低的层级,给图的下方留出很多空白,并且可能会出现很多长边。不过,由于它速度快,经常被用于分层的预处理,粗分层后再交给其他算法来进行优化。
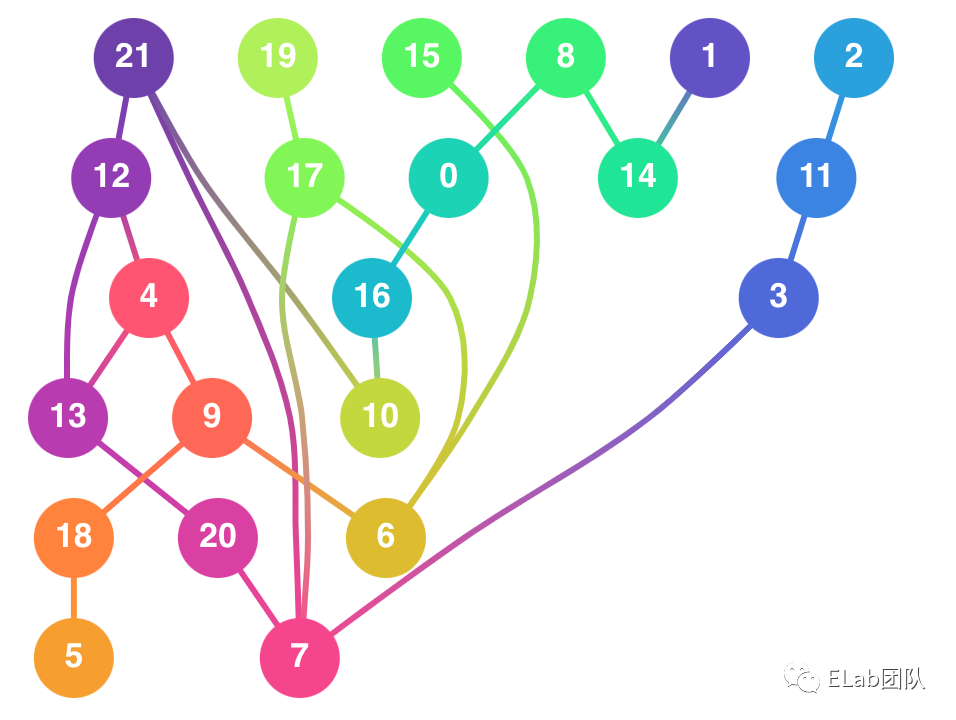
- 紧致树(Tight Tree)
紧致树算法就是一种优化方法,目的是减少长边的数量。从名称可以看出,「紧致」,即调整节点的分层,使更多边变成“紧致边”。
主要思路:
-
前提
-
每条边需要给定一个最小长度,比如1。
-
计算松弛度delta:边的长度 - 最小长度。如果松弛度为0,则为紧致边。
-
把所有紧致边和节点加入紧致生成树
-
每次取松弛度最小的边
-
如果source节点已在紧致树中,把target节点向上移delta层级
-
如果source节点不在紧致树中,把source节点向下移delta层级
-
循环,直到紧致树中已经包含了所有的节点
-
Network Simplex
-
目的:减少边的总长度(也就会减少伪节点的数量)
-
思路:
-
用紧致生成树来表示图并得到节点的层级。目的是找到一个最优的生成树。
-
边的切割值(cut value):在生成树中,如果移除某条边,图会被分成2部分,边的切割值为所有source部分指向target部分的边数减去target部分指向source部分的边数。
-
一般情况下,尽可能延长切割值为负的边可以减少边的总长度
-
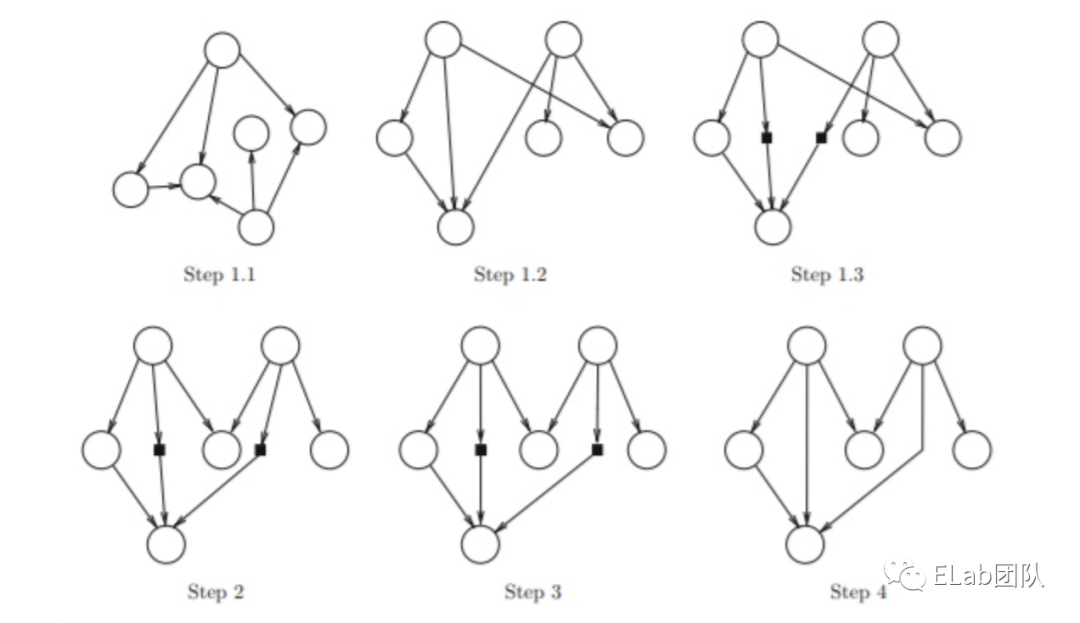
在紧致生成树的基础上,计算每条边的切割值,移除切割值为负的边,另找一条边来构建更优的生成树,直到所有的边的切割值都非负。如图(a),实线为当前的生成树,边上的数字为切割值,g->h的切割值为负,从生成树中移除后重新得到了图(b)的更优的生成树。
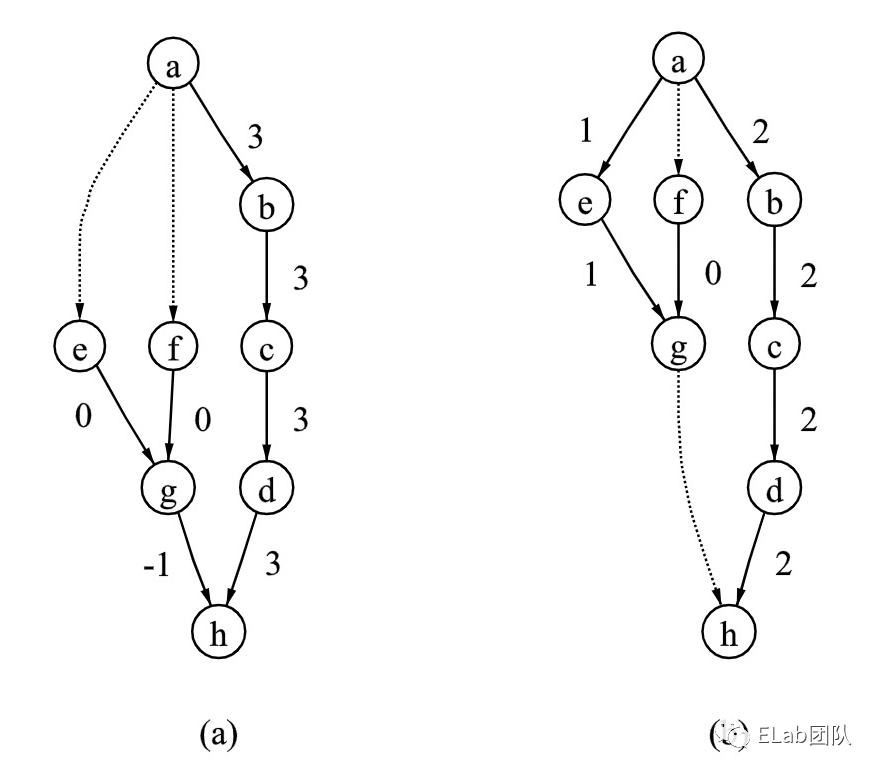
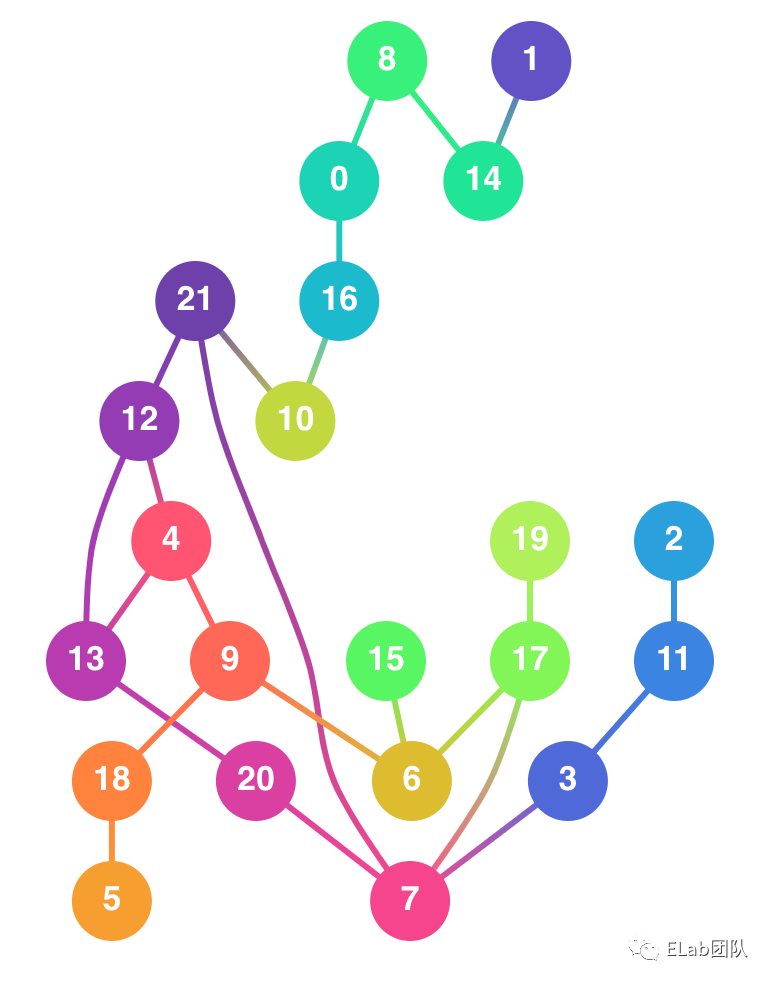
减少交叉
怎样画一个图才是美观、可理解的是比较主观的,但尽可能减少边的交叉这个标准得到了广泛的认可。
由于节点已经分层,纵坐标已确定,且对于每个长边也已经通过增加伪节点的方式被分成了相邻层之间的短边,减少边的交叉问题就变成了如何对层内节点排序的问题。
然而已经有研究证明,即使是最简单的情况,即只处理两层之间的交叉,这个问题仍是一个NP困难[5]问题。因此,很多启发式算法被提出来解决这个问题,比较经典的是重心算法和中心算法。
-
重心法(Barycenter)
-
基本原理是认为层次图中,垂直的边越多,边的交叉越少
-
一层一层从上往下&从下往上扫,每次假定层i-1中顺序固定,对层i排序来减少交叉
-
层i中每一个节点的位置由所有在层i-1上和其邻接的节点位置的平均值决定,这个值即为节点的重心值。每一层中按重心从小到大排序。
-
中心法(Median)
-
和重心定位类似,区别是它用中位的那个邻接节点的位置来计算排序值。
计算坐标
根据此前所述原则,计算每层节点的坐标主要的目的是:边尽量垂直、节点布局平衡、长边尽量直。
Sugiyama提出了一种二次规划算法(Quadratic Programming)和一种基于优先级的启发式算法(我都没看懂)。之后也有很多研究者提出了多种不同的算法。
这里介绍一下 dagre 中使用的 Brandes & Kopf 提出的一种简单快速的启发式算法,在线性时间内即可完成坐标计算。(不过这个算法似乎会导致一些异常情况,见issue[6])
- 思路:尽可能把节点和其中位的邻接节点对齐,来减少边的长度并平衡布局。
-
步骤
-
垂直对齐。
-
尝试将每个节点与其上层或下层的中位邻接节点对齐。
-
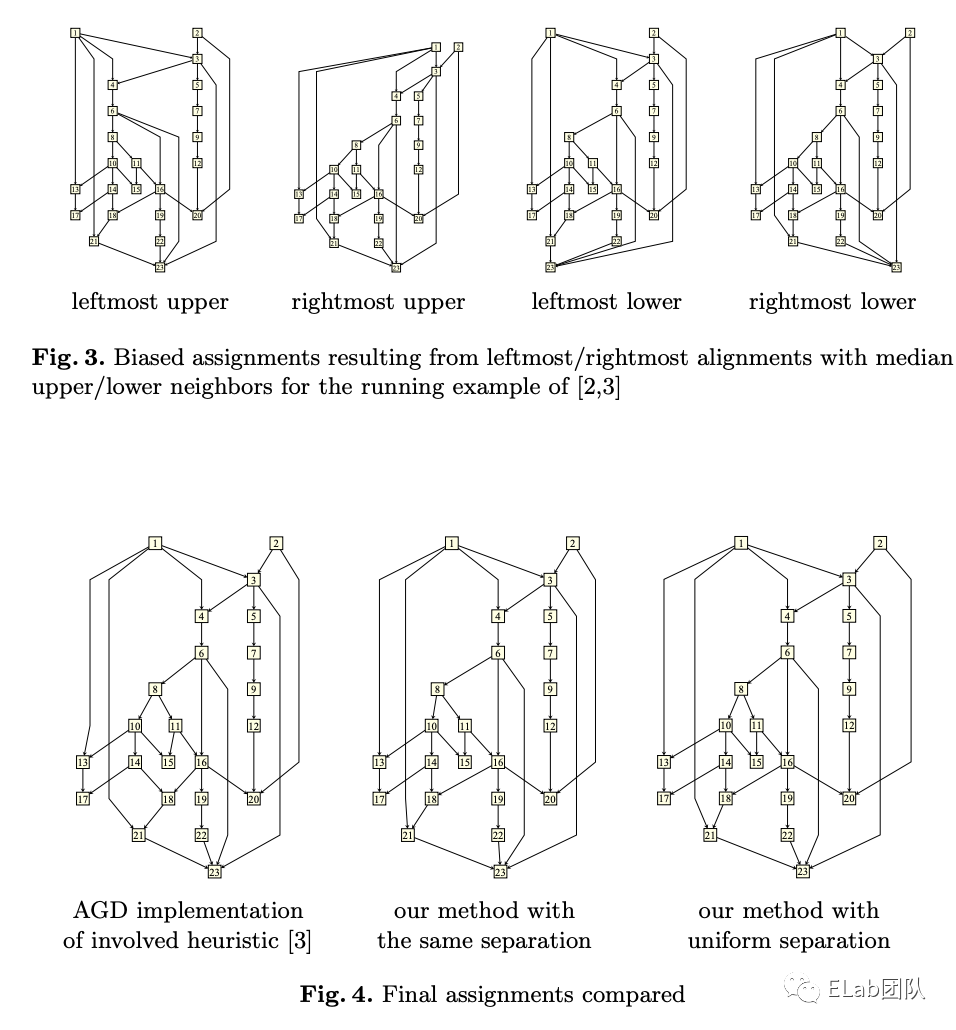
对齐的过程中可能会有冲突 - 即边交叉或连接到同一个节点时。采用左侧优先或右侧优先对齐,忽略后续冲突节点。如图(a) -> (b),是一个向上对齐、左侧优先的例子。
-
水平压缩。
-
将对齐的节点放在相同的水平坐标,如图(b) -> (c)
-
在水平方向进行压缩,使节点尽可能接近,如图(c) -> (d)
-
前两步在对齐时可以向上或向下对齐,解决冲突时可以左侧或右侧优先。因此在四个方向(左上、左下、右上、右下)上各执行一次前两步,最终结果由这四个结果平衡后得出。
其它考虑
实际布局的过程中,可能还会有更多需要考虑的点。这里列举一些供大家参考,就不详细展开了。
-
增量布局
-
在图新增节点和边时,尽量保持原有的布局不变。
-
图的嵌套
-
有时,图的节点有嵌套关系
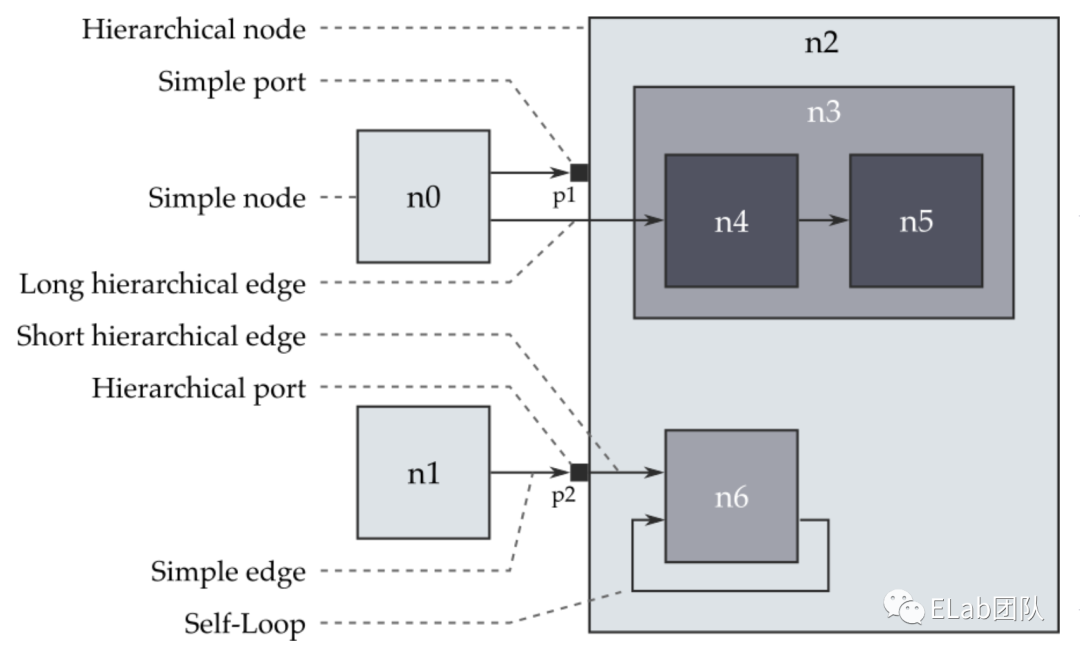
-
边的label
-
边上可能会有一些描述性的文字,计算位置时需要把label也考虑进来
-
边的画法
-
在上述的Sugiyama算法中,边是画成直线的(长边是折线)。而实际场景中,边可以展示成曲线、或水平/垂直走向的折线(Orthogonal)等等,不同的边的形式需要不同的算法来处理。
-
节点的端口
-
上述算法中,节点是被看成点,边是直接和节点相连的,而实际应用中,经常会给节点定义一些端口(ports),即指定边必须从某个端口连入或连出。
实现自己的布局
Sugiyama布局提供了图的层次布局的基本框架,而实际业务场景中的需求可能各有侧重,已有的布局方法可能无法满足要求,就需要实现自己的布局方式。
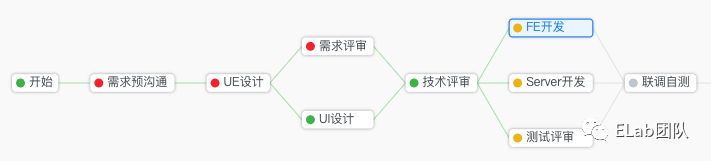
因为Sugiyama布局已经把布局分成了不同的步骤和子问题,所以比较灵活。可以对其进行调整,在不同的步骤使用不同的算法达到目的。举个例子,下图这种流程图,边的关系不复杂,没有长边,即使边有交叉也影响不大,展示的重点可能是整个图的居中的效果,那么在分层、去交叉之后,第三步计算坐标时,可以直接用简单的居中对齐的方式排布节点。
简单看一个js实现 - dagre
dagre[8]是一个实现了层次布局的 js 库,G6 就是直接引用的 dagre 来实现的层次布局。
布局流程很清晰地写在了这个runLayout方法里,虽然看起来有27步之多,整体思路还是我们上面说的:分层、减少交叉、计算坐标。而dagre也增加了一些比如去自环、去环等一些预处理,以及支持了我们上面提到一些其它能力比如:边的label、嵌套布局等。
function runLayout(g, time) { // 给边label留出空间
time("makeSpaceForEdgeLabels", function() { makeSpaceForEdgeLabels(g); }); // 去除自环
time("removeSelfEdges", function() { removeSelfEdges(g); }); // 如果有环,去环,方法是反转一些成环的边
time("acyclic", function() { acyclic.run(g); }); // 嵌套图的布局
time("nestingGraph.run", function() { nestingGraph.run(g); }); // Step 1. 分层
time("rank", function() { rank(util.asNonCompoundGraph(g)); }); // 在边的中间位置生成虚拟节点,代表label的位置
time("injectEdgeLabelProxies", function() { injectEdgeLabelProxies(g); }); // 移除空层
time("removeEmptyRanks", function() { removeEmptyRanks(g); }); // 移除虚拟根节点和虚拟边
time("nestingGraph.cleanup", function() { nestingGraph.cleanup(g); }); // 标准化rank的值
time("normalizeRanks", function() { normalizeRanks(g); }); // 找到节点组的最大和最小层级
time("assignRankMinMax", function() { assignRankMinMax(g); }); // 移除边的label虚拟节点
time("removeEdgeLabelProxies", function() { removeEdgeLabelProxies(g); }); // 把长边拆分为长度1的边,并插入虚拟节点
time("normalize.run", function() { normalize.run(g); });
time("parentDummyChains", function() { parentDummyChains(g); });
time("addBorderSegments", function() { addBorderSegments(g); }); // Step 2. 节点排序
time("order", function() { order(g); }); // 回填自环
time("insertSelfEdges", function() { insertSelfEdges(g); }); // 调整坐标系 上下/左右布局
time("adjustCoordinateSystem", function() { coordinateSystem.adjust(g); }); // Step 3. 节点定位
time("position", function() { position(g); });
time("positionSelfEdges", function() { positionSelfEdges(g); });
time("removeBorderNodes", function() { removeBorderNodes(g); }); // 移除长边插入的虚拟节点
time("normalize.undo", function() { normalize.undo(g); });
time("fixupEdgeLabelCoords", function() { fixupEdgeLabelCoords(g); });
time("undoCoordinateSystem", function() { coordinateSystem.undo(g); });
time("translateGraph", function() { translateGraph(g); }); // 计算边和节点的交点
time("assignNodeIntersects", function() { assignNodeIntersects(g); }); // 反转在去环阶段被反转的边
time("reversePoints", function() { reversePointsForReversedEdges(g); });
time("acyclic.undo", function() { acyclic.undo(g); }); }
总结
-
本文主要介绍了图的层次布局的基本思路、步骤和相关算法
-
层次布局主要分为4步:节点分层、减少交叉、计算坐标、画图。或者是5步(即包括首先通过去环算法把有环图转换成无环图)
-
每一步都是一个复杂的子问题,有很多启发式算法被提出来解决相关问题,在具体业务场景的基础上,也可以使用自己的算法解决问题。
参考资料
[1]G6: https://g6.antv.vision/
[2]层次布局: https://en.wikipedia.org/wiki/Layered_graph_drawing
[3]d3-dag: https://observablehq.com/@erikbrinkman/d3-dag-sugiyama
[4]d3-dag: https://observablehq.com/@erikbrinkman/d3-dag-sugiyama
[5]NP困难: https://en.wikipedia.org/wiki/NP-hardness
[6]issue: https://github.com/dagrejs/dagre/issues/239
[7]ELK: https://www.eclipse.org/elk/documentation/tooldevelopers/graphdatastructure.html
[8]dagre: https://github.com/dagrejs/dagre
[9]Github - dagre/dagre: https://github.com/dagrejs/dagre
[10]Github - d3-dag: https://github.com/erikbrinkman/d3-dag
[11]G6: https://g6.antv.vision/
[12]Eclipse Layout Kernel: https://www.eclipse.org/elk/
[13]Wiki - Layered Graph Drawing: https://en.wikipedia.org/wiki/Layered_graph_drawing
[14]图可视化之图布局: https://zhuanlan.zhihu.com/p/346059370
[15]深入解读Dagre布局算法: https://www.yuque.com/antv/g6-blog/xxp5nl
[16]Methods for Visual Understanding of Hierarchical System Structures: https://ieeexplore.ieee.org/document/4308636/
[17]A Technique for Drawing Directed Graphs: https://www.researchgate.net/profile/Emden-Gansner/publication/3187542_A_Technique_for_Drawing_Directed_Graphs/links/5c0abd024585157ac1b04523/A-Technique-for-Drawing-Directed-Graphs.pdf
[18]Fast and Simple Horizontal Coordinate Assignment: https://link.springer.com/content/pdf/10.1007%2F3-540-45848-4_3.pdf
[19]Layout of Compound Directed Graphs: https://publikationen.sulb.uni-saarland.de/bitstream/20.500.11880/25862/1/tr-A03-96.pdf
[20]An Efficient Implementation of Sugiyama’s Algorithm for Layered Graph Drawing: https://link.springer.com/content/pdf/10.1007%2F978-3-540-31843-9_17.pdf
[21]Port Constraints in Hierarchical Layout of Data Flow Diagrams: https://link.springer.com/content/pdf/10.1007%2F978-3-642-11805-0_14.pdf
[22]Improved Vertical Segment Routing for Sugiyama Layouts: https://rtsys.informatik.uni-kiel.de/~biblio/downloads/theses/thw-bt.pdf