HashMap连环18问

对于 JAVA 求职者来说，HashMap 可谓是重中之重，是面试必考点。然而 HashMap 的知识点非常多，复习起来花费精力很大，库森当年校招面试时就经历过这种痛苦。所以，结合自己的面试经验，斗胆写一篇关于 HashMap 的面试专题文章，希望对小伙伴有所帮助!

1 . 存储结构

HashMap 的底层数据结构是什么？

在 JDK1.7 和 JDK1.8 中有所差别：

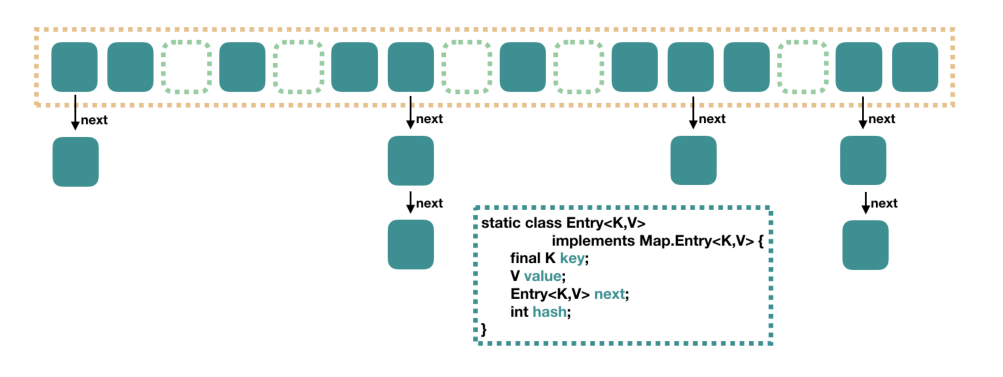
在 JDK1.7 中，由“数组+链表”组成，数组是 HashMap 的主体，链表则是主要为了解决哈希冲突而存在的。

在 JDK1.8 中，由“数组+链表+红黑树”组成。当链表过长，则会严重影响 HashMap 的性能，红黑树搜索时间复杂度是 O(logn)，而链表是糟糕的 O(n)。因此，JDK1.8 对数据结构做了进一步的优化，引入了红黑树，链表和红黑树在达到一定条件会进行转换：

• 当链表长度超过 8 且数据总量大于等于 64 才会转红黑树。
• 将链表转换成红黑树前会判断，如果当前数组的长度小于 64，那么会选择先进行数组扩容，而不是转换为红黑树，以减少搜索时间。

JDK1.7 HashMap结构 JDK1.8 HashMap结构

更深入的面试问题，

为什么在解决 hash 冲突的时候，不直接用红黑树？而选择先用链表，再转红黑树?

因为红黑树需要进行左旋，右旋，变色这些操作来保持平衡，而单链表不需要。当元素小于 8 个的时候，此时做查询操作，链表结构已经能保证查询性能。当元素大于 8 个的时候， 红黑树搜索时间复杂度是 O(logn)，而链表是 O(n)，此时需要红黑树来加快查询速度，但是新增节点的效率变慢了。

因此，如果一开始就用红黑树结构，元素太少，新增效率又比较慢，无疑这是浪费性能的。

不用红黑树，用二叉查找树可以么?

可以。但是二叉查找树在特殊情况下会变成一条线性结构（这就跟原来使用链表结构一样了，造成很深的问题），遍历查找会非常慢。

当链表转为红黑树后，什么时候退化为链表?

为6的时候退转为链表。中间有个差值7可以防止链表和树之间频繁的转换。假设一下，如果设计成链表个数超过8则链表转换成树结构，链表个数小于8则树结构转换成链表，如果一个HashMap不停的插入、删除元素，链表个数在8左右徘徊，就会频繁的发生树转链表、链表转树，效率会很低。

为什么链表改为红黑树的阈值是 8?

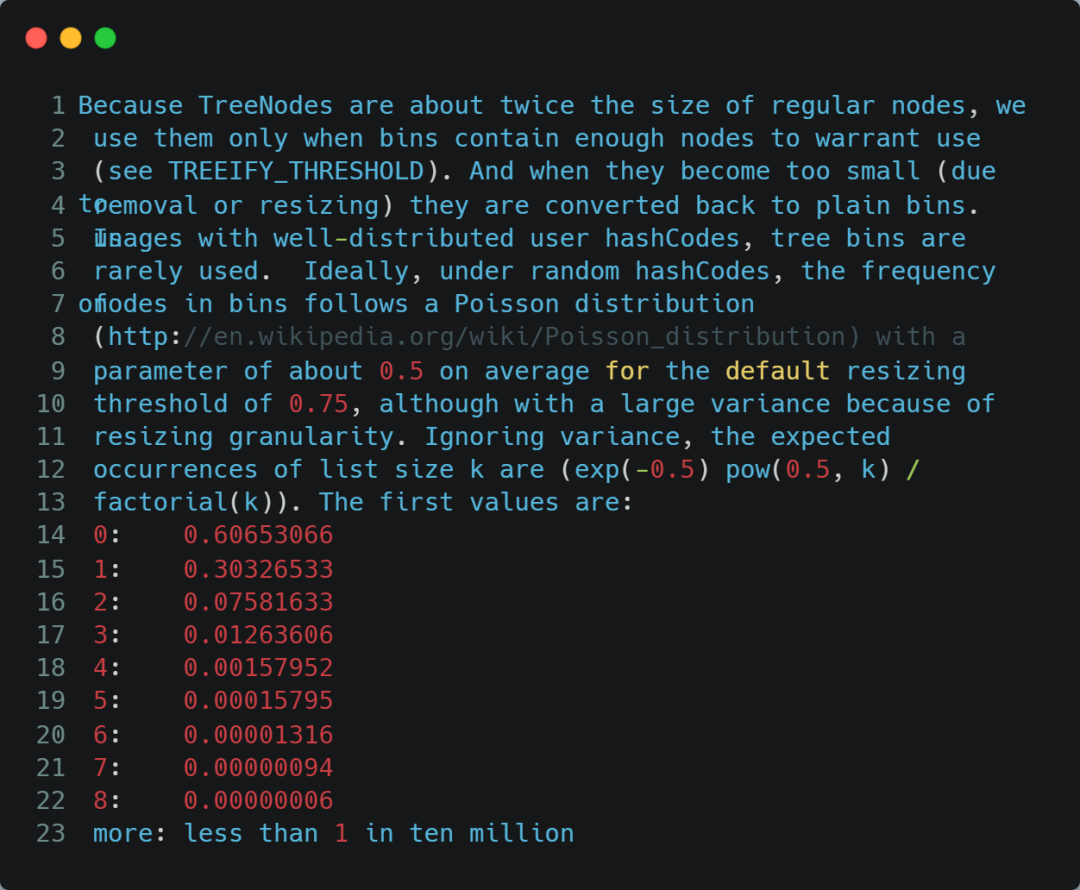
是因为泊松分布，我们来看作者在源码中的注释：

翻译过来大概的意思是：理想情况下使用随机的哈希码，容器中节点分布在 hash 桶中的频率遵循泊松分布，按照泊松分布的计算公式计算出了桶中元素个数和概率的对照表，可以看到链表中元素个数为 8 时的概率已经非常小，再多的就更少了，所以原作者在选择链表元素个数时选择了 8，是根据概率统计而选择的。

字段结构

默认加载因子是多少？为什么是 0.75，不是 0.6 或者 0.8 ？

回答这个问题前，我们来先看下HashMap的默认构造函数：

Node[] table的初始化长度length(默认值是16)，Load factor为负载因子(默认值是0.75)，threshold是HashMap所能容纳键值对的最大值。threshold = length * Load factor。也就是说，在数组定义好长度之后，负载因子越大，所能容纳的键值对个数越多。

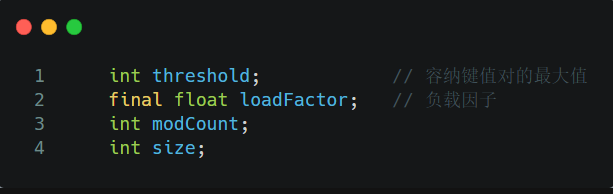
默认的loadFactor是0.75，0.75是对空间和时间效率的一个平衡选择，一般不要修改，除非在时间和空间比较特殊的情况下 ：

• 如果内存空间很多而又对时间效率要求很高，可以降低负载因子Load factor的值 。
• 相反，如果内存空间紧张而对时间效率要求不高，可以增加负载因子loadFactor的值，这个值可以大于1。

我们来追溯下作者在源码中的注释（JDK1.7）：

翻译过来大概的意思是：作为一般规则，默认负载因子（0.75）在时间和空间成本上提供了很好的折衷。较高的值会降低空间开销，但提高查找成本（体现在大多数的HashMap类的操作，包括get和put）。设置初始大小时，应该考虑预计的entry数在map及其负载系数，并且尽量减少rehash操作的次数。如果初始容量大于最大条目数除以负载因子，rehash操作将不会发生。

2 . 索引计算

HashMap 中 key 的存储索引是怎么计算的？

首先根据key的值计算出hashcode的值，然后根据hashcode计算出hash值，最后通过hash&（length-1）计算得到存储的位置。看看源码的实现：

jdk1.7 索引计算 jdk1.8 索引计算

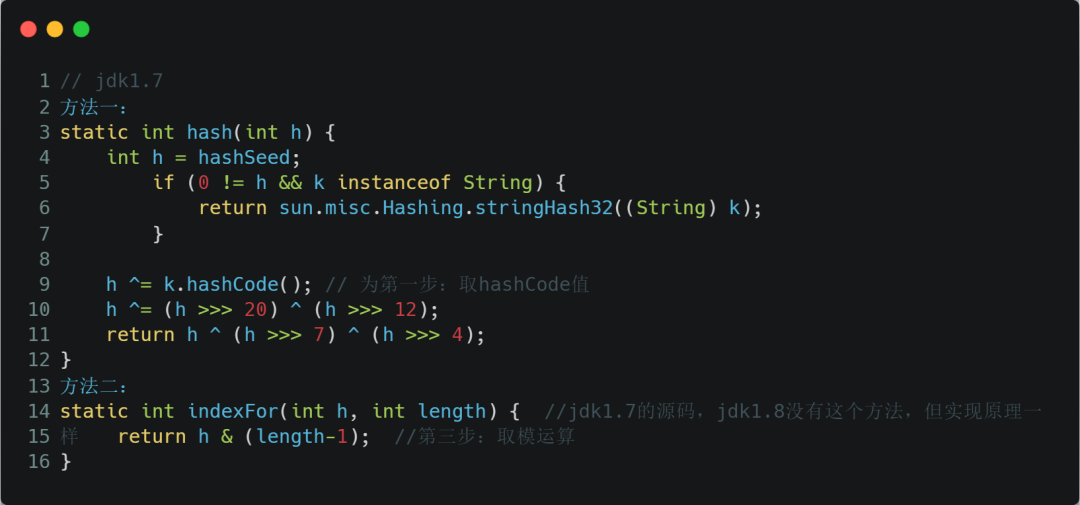
这里的 Hash 算法本质上就是三步：取key的 hashCode 值、根据 hashcode 计算出hash值、通过取模计算下标。其中，JDK1.7和1.8的不同之处，就在于第二步。我们来看下详细过程，以JDK1.8为例，n为table的长度：

扩展出以下几个问题，

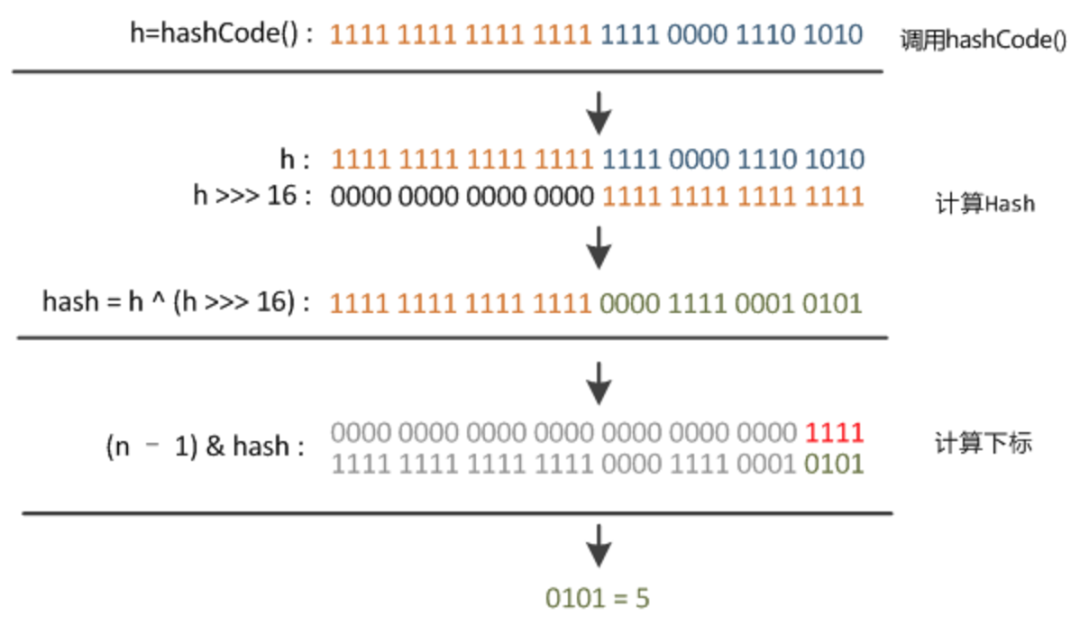
JDK1.8 为什么要 hashcode 异或其右移十六位的值？

因为在JDK 1.7 中扰动了 4 次，计算 hash 值的性能会稍差一点点。从速度、功效、质量来考虑，JDK1.8 优化了高位运算的算法，通过hashCode()的高16位异或低16位实现：(h = k.hashCode()) ^ (h >>> 16)。这么做可以在数组 table 的 length 比较小的时候，也能保证考虑到高低Bit都参与到Hash的计算中，同时不会有太大的开销。

为什么 hash 值要与length-1相与？

• 把 hash 值对数组长度取模运算，模运算的消耗很大，没有位运算快。
• 当 length 总是 2 的n次方时，h& (length-1) 运算等价于对length取模，也就是 h%length，但是 & 比 % 具有更高的效率。

HashMap数组的长度为什么是 2 的幂次方？

这样做效果上等同于取模，在速度、效率上比直接取模要快得多。除此之外，2 的 N 次幂有助于减少碰撞的几率。如果 length 为2的幂次方，则 length-1 转化为二进制必定是11111……的形式，在与h的二进制与操作效率会非常的快，而且空间不浪费。我们来举个例子，看下图：

当n=15时，6 和 7 的结果一样，这样表示他们在 table 存储的位置是相同的，也就是产生了碰撞，6、7就会在一个位置形成链表，4和5的结果也是一样，这样就会导致查询速度降低。

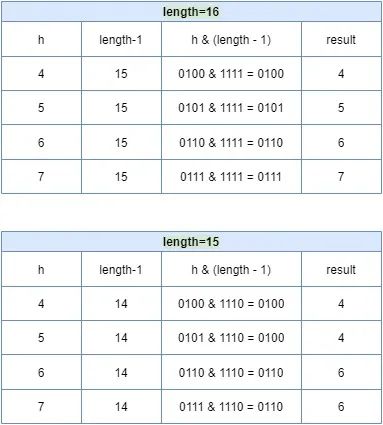
如果我们进一步分析，还会发现空间浪费非常大，以 length=15 为例，在 1、3、5、7、9、11、13、15 这八处没有存放数据。因为hash值在与14（即 1110）进行&运算时，得到的结果最后一位永远都是0，即 0001、0011、0101、0111、1001、1011、1101、1111位置处是不可能存储数据的。

补充数组容量计算的小奥秘

HashMap 构造函数允许用户传入的容量不是 2 的 n 次方，因为它可以自动地将传入的容量转换为 2 的 n 次方。会取大于或等于这个数的 且最近的2次幂作为 table 数组的初始容量，使用tableSizeFor(int)方法，如 tableSizeFor(10) = 16（2 的 4 次幂），tableSizeFor(20) = 32（2 的 5 次幂），也就是说 table 数组的长度总是 2 的次幂。JDK1.8 源码如下：

3 . put方法

HashMap 的put方法流程？

简要流程如下：

1. 首先根据 key 的值计算 hash 值，找到该元素在数组中存储的下标；
2. 如果数组是空的，则调用 resize 进行初始化；
3. 如果没有哈希冲突直接放在对应的数组下标里；
4. 如果冲突了，且 key 已经存在，就覆盖掉 value；
5. 如果冲突后，发现该节点是红黑树，就将这个节点挂在树上；
6. 如果冲突后是链表，判断该链表是否大于 8 ，如果大于 8 并且数组容量小于 64，就进行扩容；
7. 如果链表长度大于 8 并且数组的容量大于等于 64，则将这个结构转换为红黑树；
8. 否则，链表插入键值对，若 key 存在，就覆盖掉 value。

hashmap之put方法 (JDK1.8)

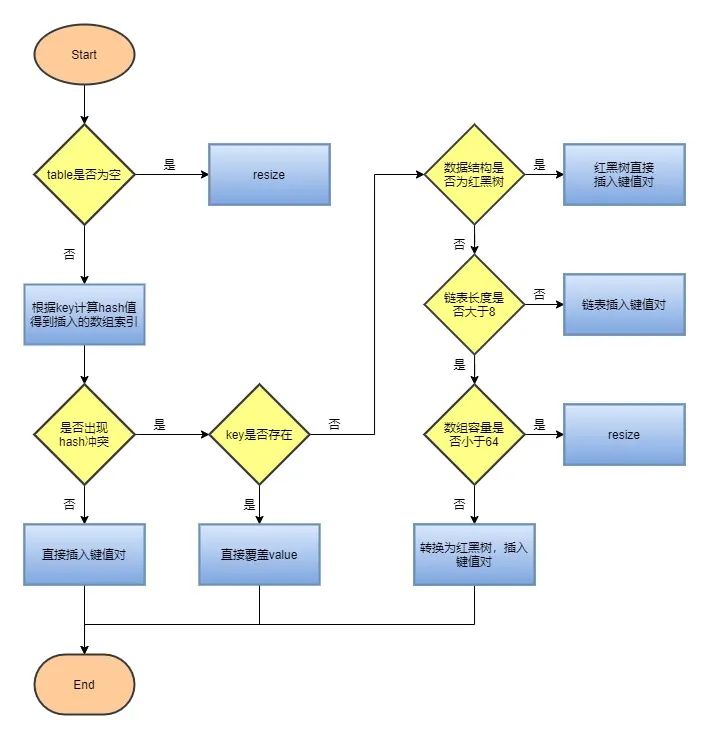
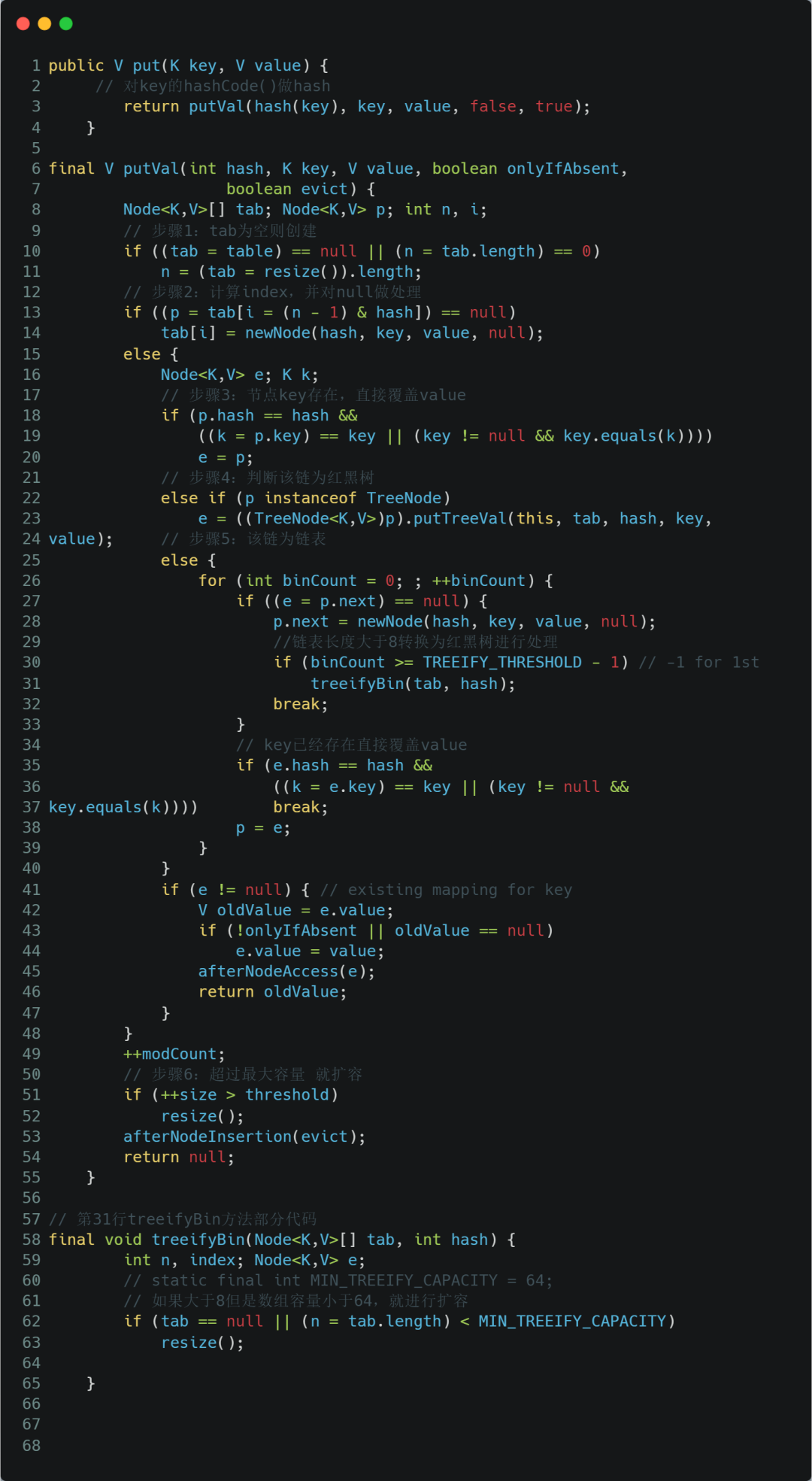
详细分析，见 JDK1.8 的 put 方法源码:

扩展的问题

JDK1.7 和1.8 的put方法区别是什么？

区别在两处：

解决哈希冲突时，JDK1.7 只使用链表，JDK1.8 使用链表+红黑树，当满足一定条件，链表会转换为红黑树。

链表插入元素时，JDK1.7 使用头插法插入元素，在多线程的环境下有可能导致环形链表的出现，扩容的时候会导致死循环。因此，JDK1.8使用尾插法插入元素，在扩容时会保持链表元素原本的顺序，就不会出现链表成环的问题了，但JDK1.8 的 HashMap 仍然是线程不安全的，具体原因会在另一篇文章分析。

4 . 扩容机制

HashMap 的扩容方式？

Hashmap 在容量超过负载因子所定义的容量之后，就会扩容。Java 里的数组是无法自动扩容的，方法是将 Hashmap 的大小扩大为原来数组的两倍，并将原来的对象放入新的数组中。

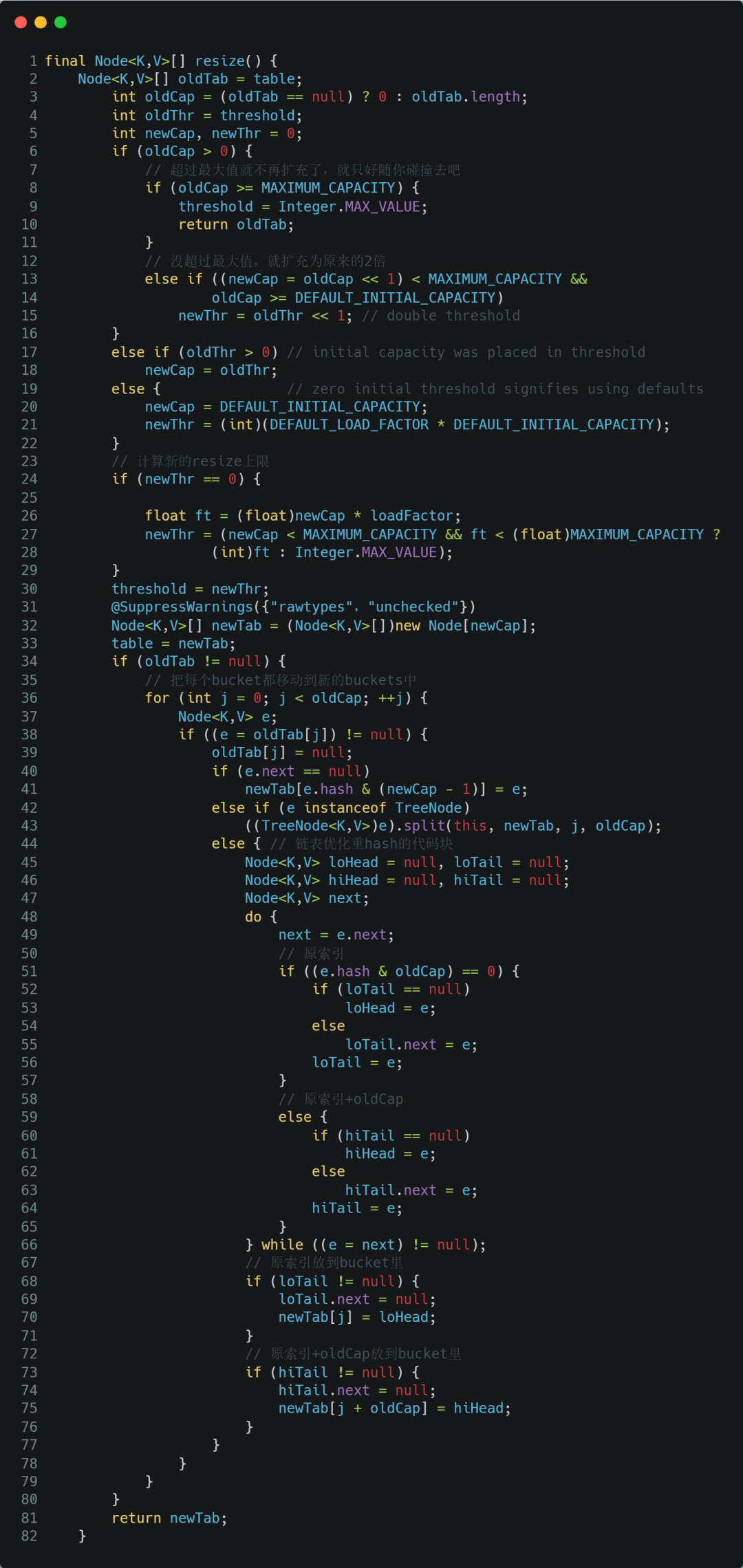
那扩容的具体步骤是什么？让我们看看源码。

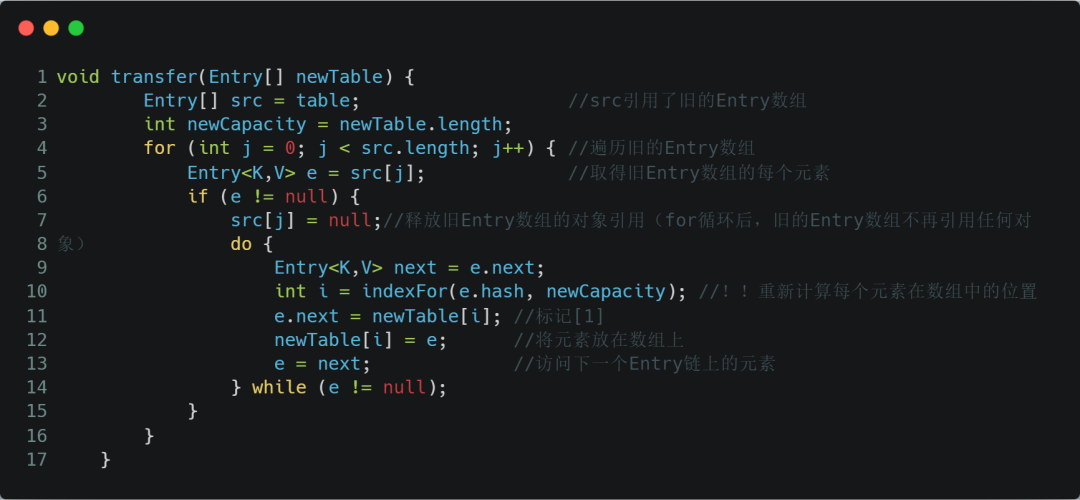
先来看下 JDK1.7 的代码：

这里就是使用一个容量更大的数组来代替已有的容量小的数组，transfer()方法将原有Entry数组的元素拷贝到新的Entry数组里。

newTable[i] 的引用赋给了 e.next ，也就是使用了单链表的头插入方式，同一位置上新元素总会被放在链表的头部位置；这样先放在一个索引上的元素终会被放到 Entry 链的尾部(如果发生了 hash 冲突的话）。

JDK1.8的优化

扩容在JDK1.8中有什么不一样？

JDK1.8做了两处优化：

1. resize 之后，元素的位置在原来的位置，或者原来的位置 +oldCap (原来哈希表的长度）。不需要像 JDK1.7 的实现那样重新计算hash ，只需要看看原来的 hash 值新增的那个bit是1还是0就好了，是0的话索引没变，是1的话索引变成“原索引 + oldCap ”。这个设计非常的巧妙，省去了重新计算 hash 值的时间。

如下图所示，n 为 table 的长度，图（a）表示扩容前的 key1 和 key2 两种 key 确定索引位置的示例，图（b）表示扩容后 key1 和key2 两种 key 确定索引位置的示例，其中 hash1 是 key1 对应的哈希与高位运算结果。

元素在重新计算 hash 之后，因为 n 变为 2倍，那么 n-1 的 mask 范围在高位多 1 bit(红色)，因此新的index就会发生这样的变化：

2 . JDK1.7 中 rehash 的时候，旧链表迁移新链表的时候，如果在新表的数组索引位置相同，则链表元素会倒置（头插法）。JDK1.8 不会倒置，使用尾插法。

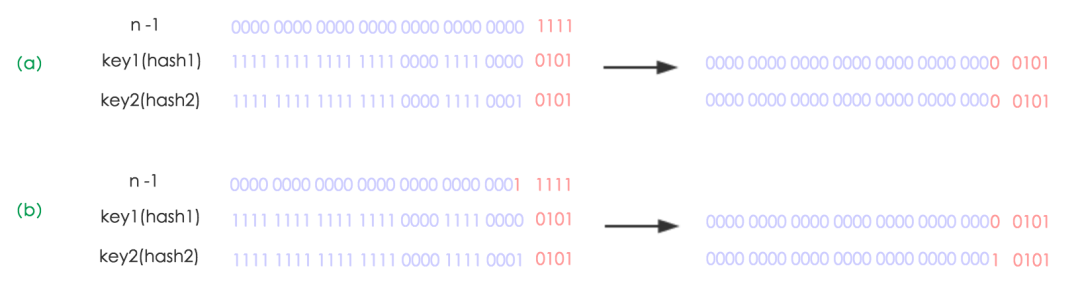
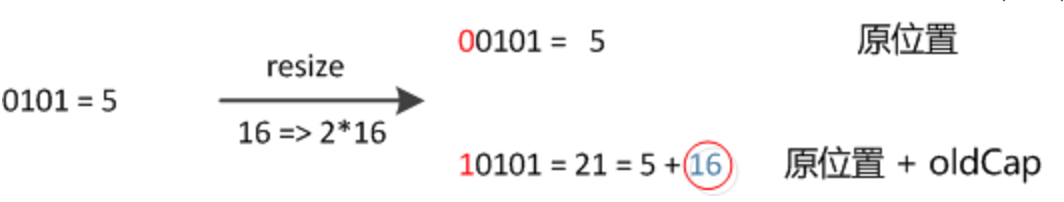
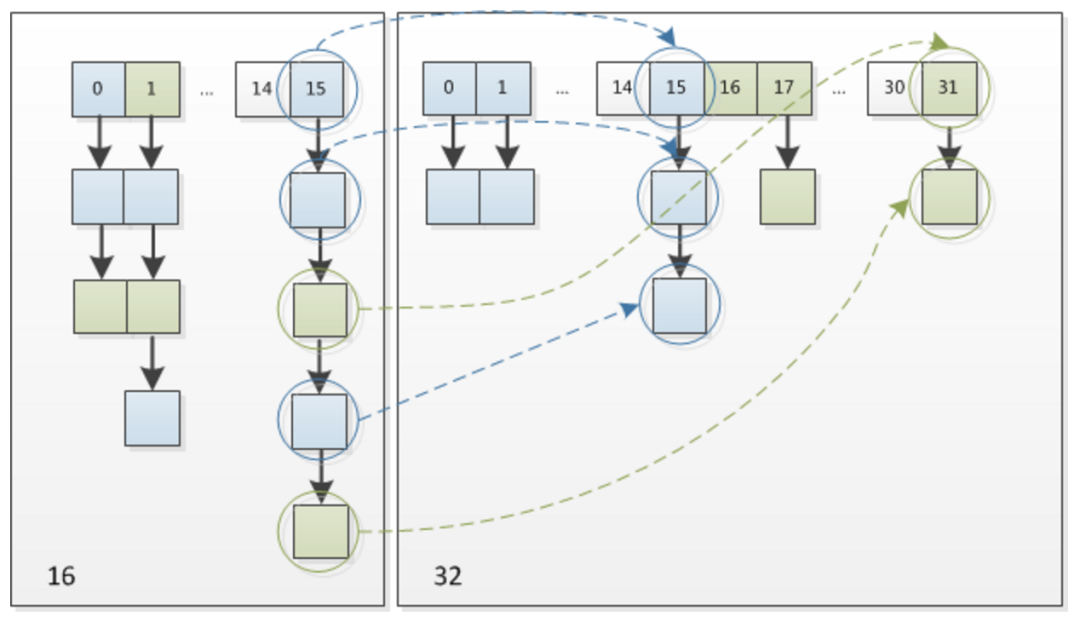
下图为 16扩充为 32 的 resize 示意图：

感兴趣的小伙伴可以看下 JDK1.8 的 resize 源码：

5 . 其他

还知道哪些hash算法？

Hash函数是指把一个大范围映射到一个小范围，目的往往是为了节省空间，使得数据容易保存。比较出名的有MurmurHash、MD4、MD5等等。

key 可以为 Null 吗?

可以，key 为 Null 的时候，hash算法最后的值以0来计算，也就是放在数组的第一个位置。

一般用什么作为HashMap的key?

一般用Integer、String 这种不可变类当 HashMap 当 key，而且 String 最为常用。

• 因为字符串是不可变的，所以在它创建的时候 hashcode 就被缓存了，不需要重新计算。这就是 HashMap 中的键往往都使用字符串的原因。
• 因为获取对象的时候要用到 equals() 和 hashCode() 方法，那么键对象正确的重写这两个方法是非常重要的,这些类已经很规范的重写了 hashCode() 以及 equals() 方法。

用可变类当 HashMap 的 key 有什么问题?

hashcode 可能发生改变，导致 put 进去的值，无法 get 出。如下所示：

hashcode

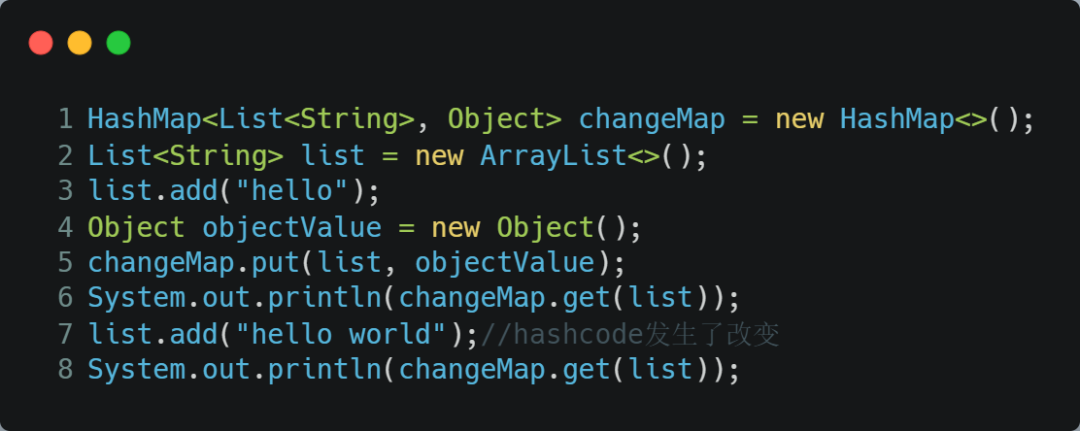
案例输出值如下

hashcode案例续

最后

以上便是 HashMap 的核心面试题了，限于篇幅原因，本文并没有讲到 HashMap 的线程不安全问题，后面会专门写一篇文章讲解，敬请期待呦！