面试官:堆排序是怎么排的?
今天我们来聊重要的堆排序。堆排序在面试中是常考的内容,而且,堆也常用于处理各种海量数据面试题。
我们先看看究竟什么是堆?以大顶堆为例:
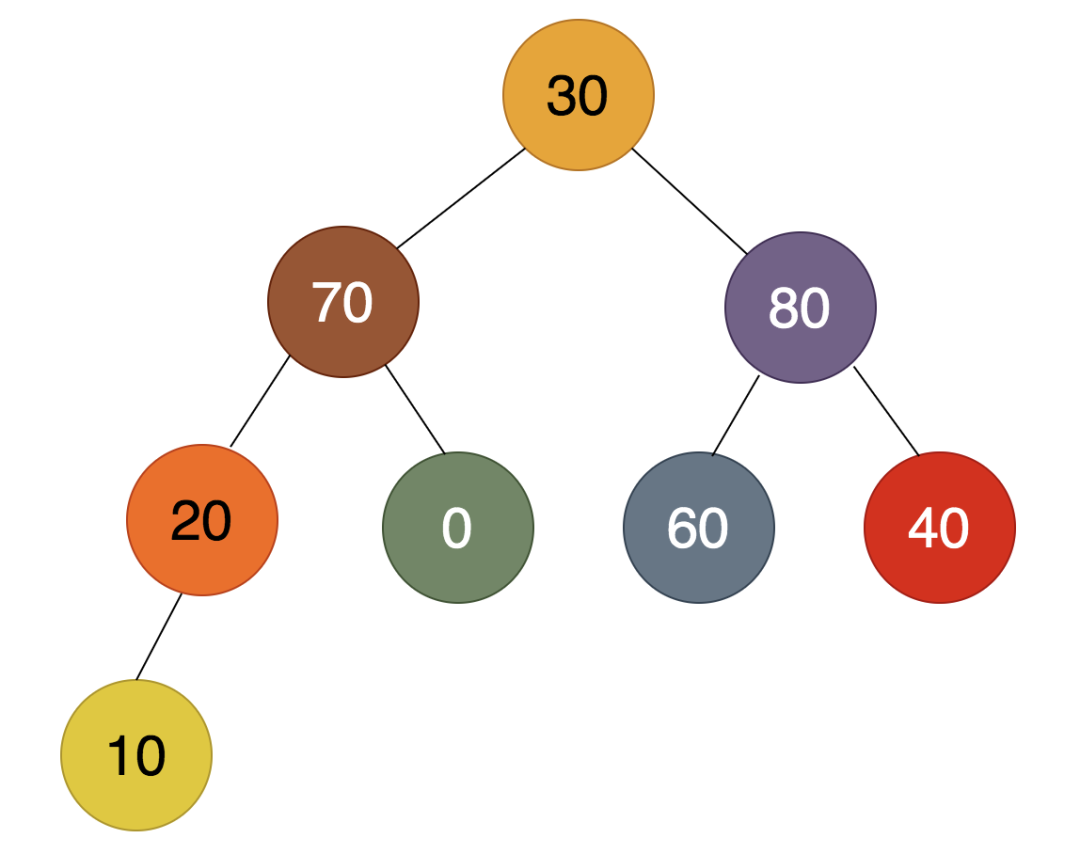
对于一棵完全二叉树而言,当每个结点不小于其子结点时,便可称之为堆(大顶堆),比如:
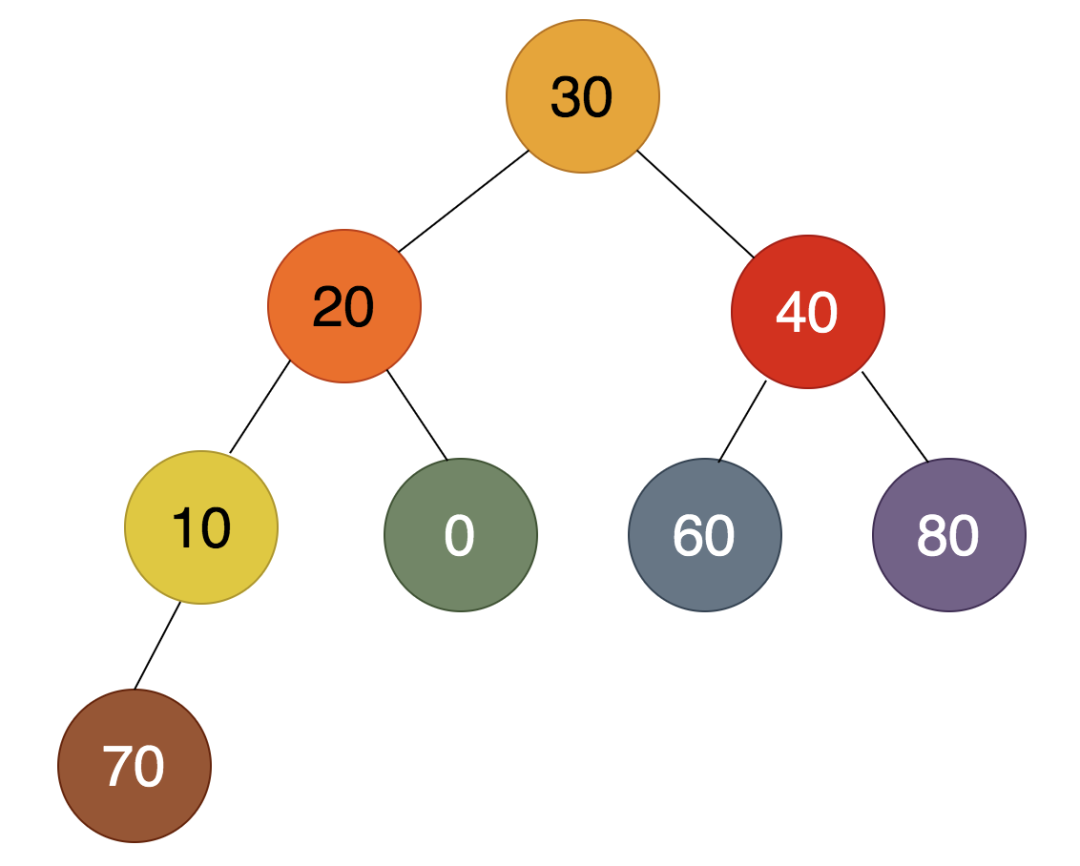
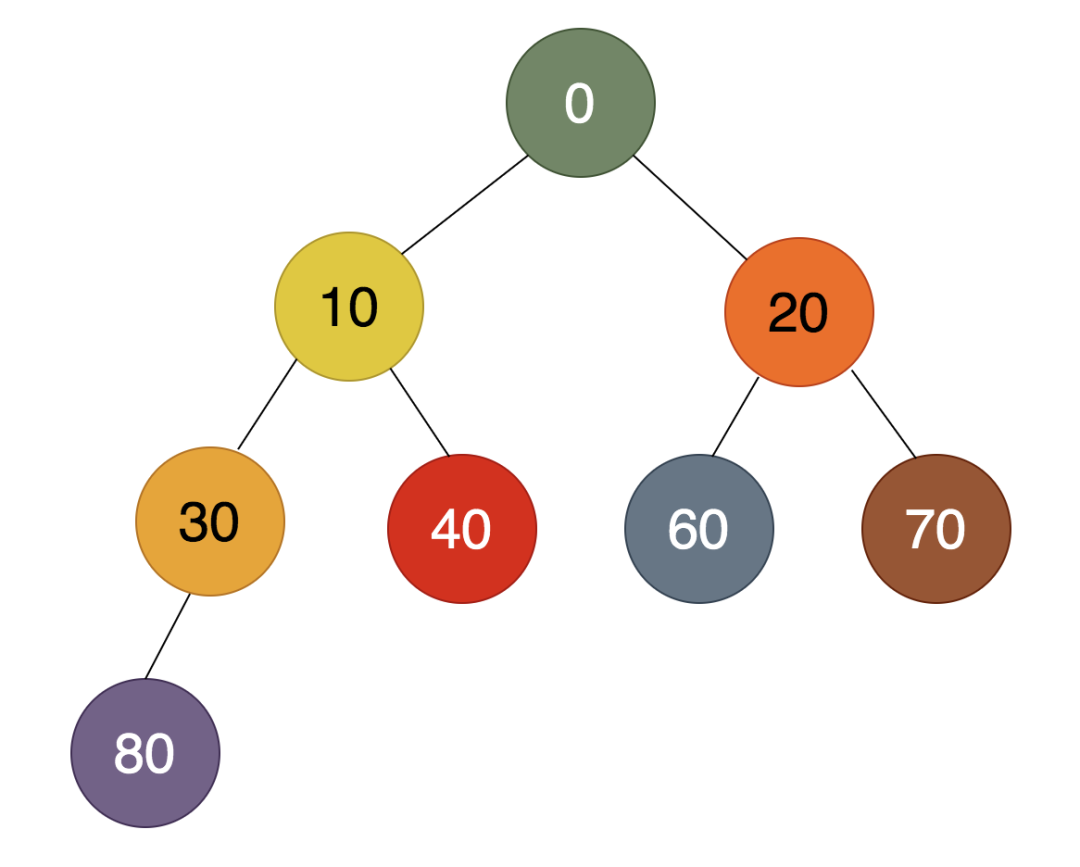
原始的待排序的数组为:30, 20, 40, 10, 0, 60, 80, 70其对应的完全二叉树为:
接下来,我们来图解堆排序,并用程序来实现堆排序。在这个过程中,希望大家感受到堆之美。
图解堆排序
一. 构建堆
第1步:
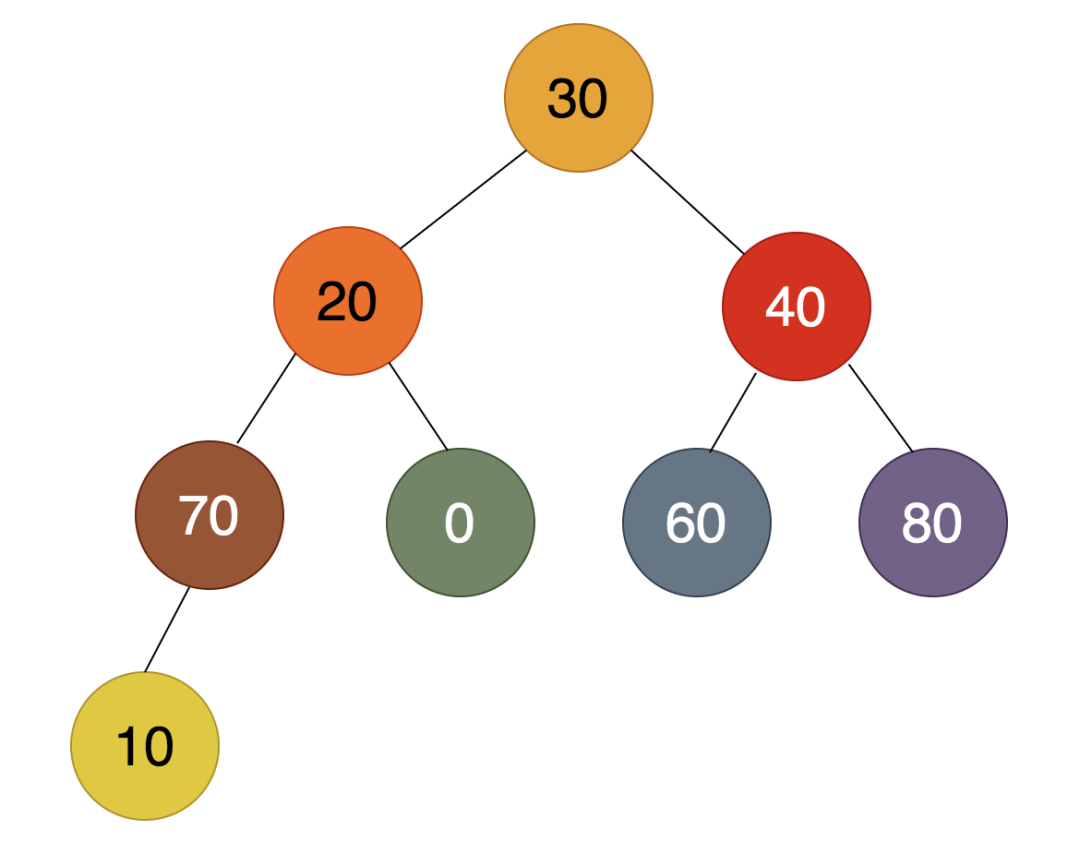
如上图,最后一个非叶子结点是10,发现10比70小,所以70必须上浮,得到的结果为:
第2步:
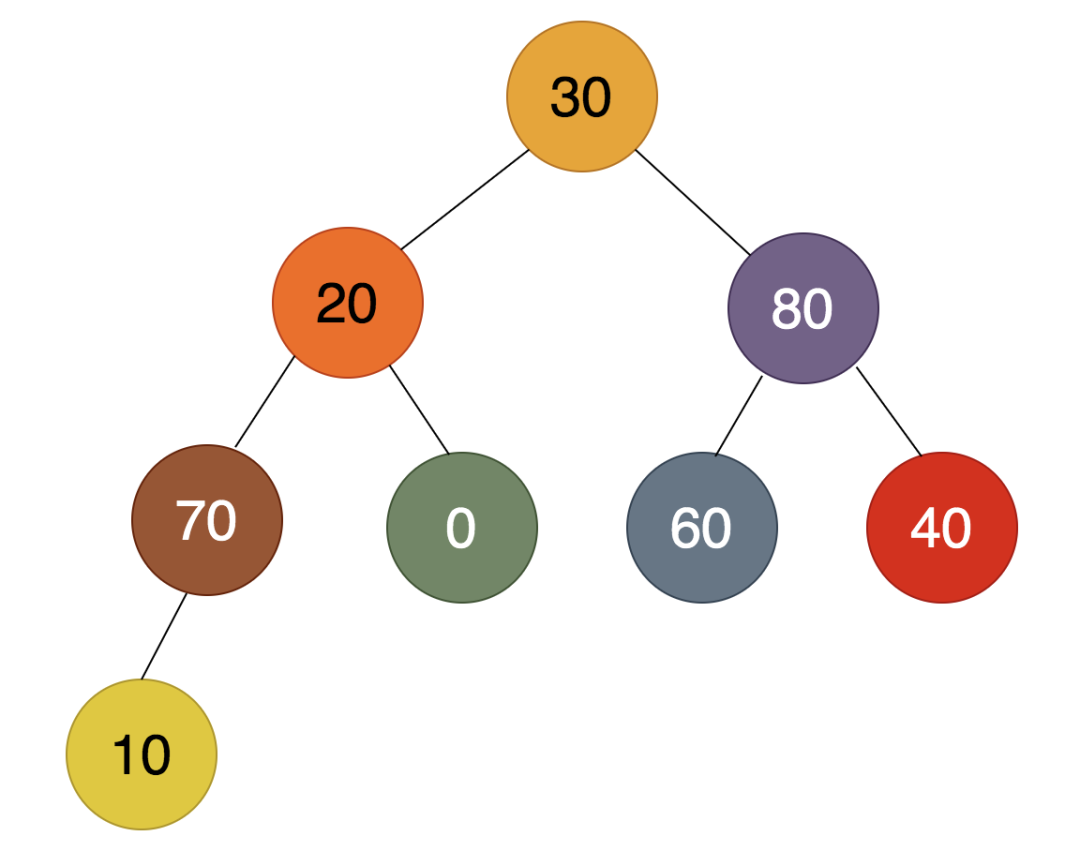
如上图,倒数第二个非叶子结点为40,在40,60,80这三个数中,80最大,所以80必须上浮,得到的结果如下:
第3步:
如上图,倒数第三个非叶子结点为20,而20比70小,所以70必须上浮,20下沉后,发现比下面的10还大,所以没有必要沉底,得到的结果为:
第4步:
如上图,倒数第四个非叶子结点为30,在30,70,80中,80最大,所以80要上浮,30下沉。然而,30比60和40都小,所以要继续下沉,得到的结果是:
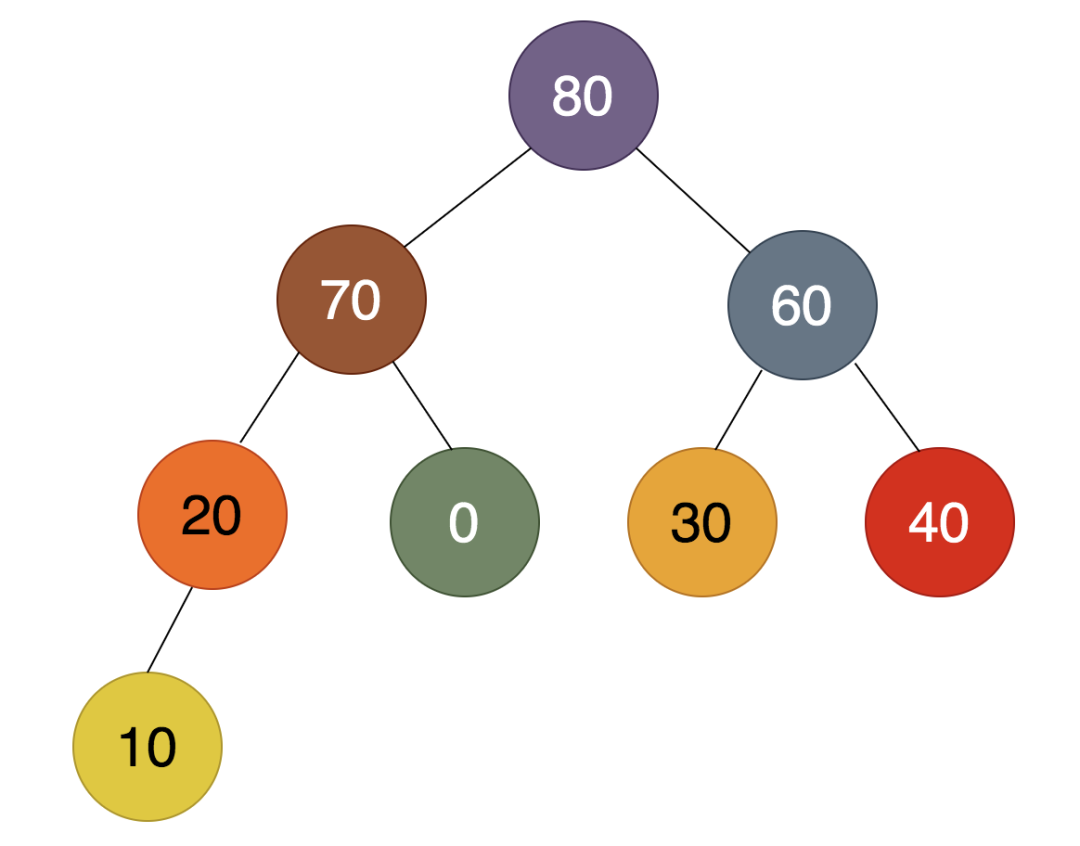
到此为止,可以看到,一个大顶堆已经形成,可以看到,最大的80已经被选择出来了。
二. 调整堆
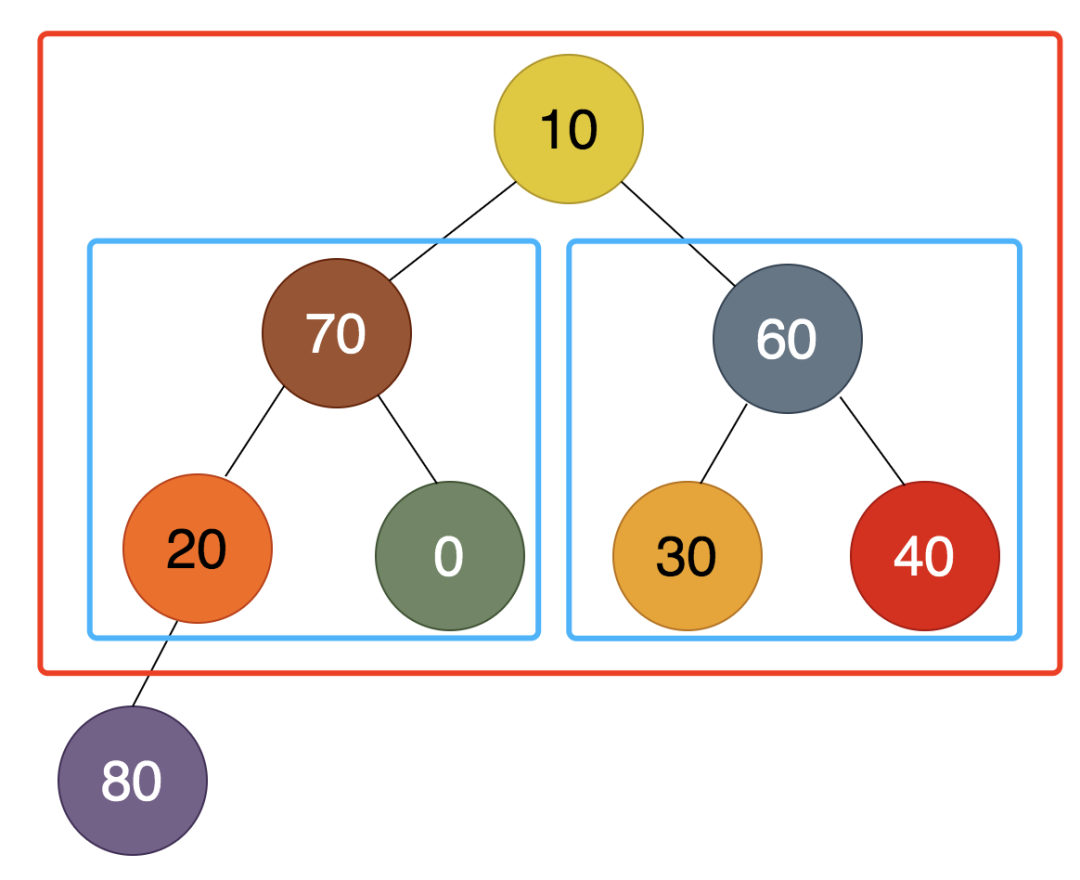
我们把堆顶的最大值80调整到最后,保存下来,得到的结果是:
接下来的工作就是对上面红框中的的7个结点进行调整,使之形成新的堆。
很显然,根据之前调整的过程可知,两个蓝色框中的结点,已经分别成堆了,所以这次的调整就简单多了,直接瞄准待调整的10即可。
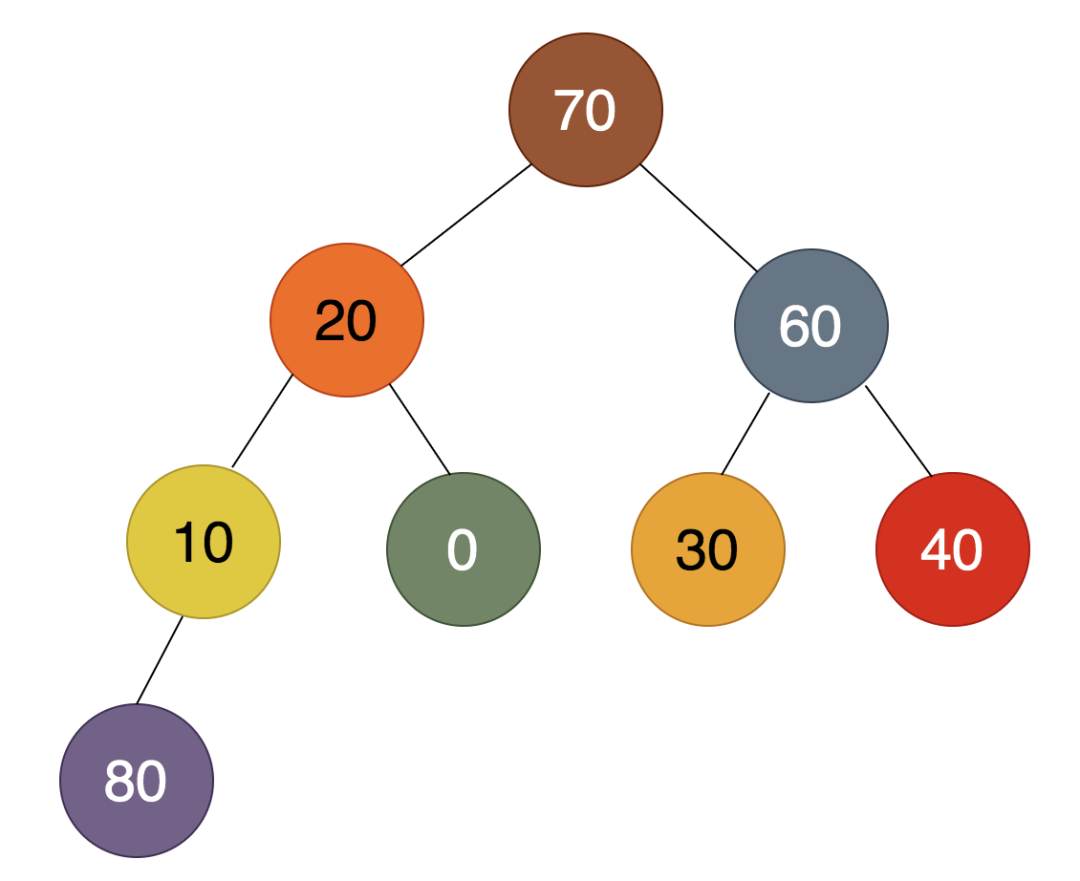
之前已经把8个结点调整成堆,那么调整上面红色框中的7个结点成堆便不在话下。于是,这7个结点中最大的70被调到了堆顶,如下:
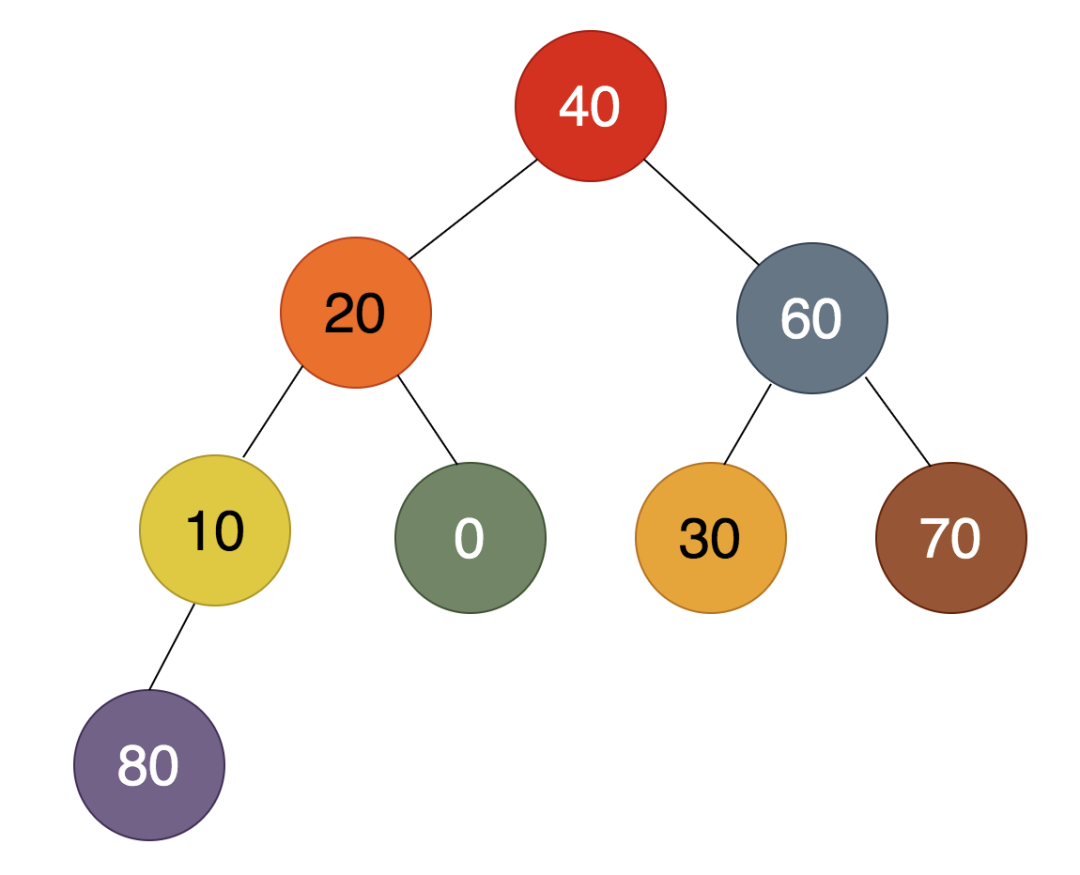
80是最大的值,放在最后。堆顶的70是第二大的值,放在倒数第二的位置,所以跟40进行交换,得到的结果为:
可见,通过2次从堆顶摘下最大元素,分别把80和70选出来了。接下来,用相同的方法,把60选出来,依此循环,最后得到的二叉树为:
终于,实现了排序,这就是所谓的堆排序,其平均时间复杂度为O(N*logN), 比冒泡排序好多啦。
堆排序实现
接下来,我们用代码来实现堆排序,如下:
#include<iostream>
using namespace std;
void print(int a[], int n)
{
int i;
for(i = 0; i < n; i++)
{
cout << a[i] << " ";
}
cout << endl;
}
void heapAdjust(int a[], int low, int high)
{
int pivotKey = a[low - 1];
int i;
for(i = 2 * low; i <= high; i *= 2)
{
if(i < high && a[i - 1] < a[i])
{
i++; //i指向较大值
}
if(pivotKey >= a[i - 1])
{
break;
}
a[low - 1] = a[i - 1];
low = i;
}
a[low - 1] = pivotKey;
}
void heapSort(int a[], int n)
{
int i, tmp;
for(i = n/2; i > 0; i--)
{
heapAdjust(a, i, n);
print(a, n);
}
for(i = n; i > 1; i--)
{
tmp = a[i -1];
a[i - 1] = a[0];
a[0] = tmp;
heapAdjust(a, 1, i - 1);
print(a, n);
}
}
int main()
{
int a[] = {30, 20, 40, 10, 0, 60, 80, 70};
int n = sizeof(a) / sizeof(a[0]);
heapSort(a, n);
print(a, n);
return 0;
}最终的排序结果如下:
0 10 20 30 40 60 70 80
堆是一种重要的数据结构,堆排序也是非常重要的算法。在笔试面试中,经常考到堆的相关应用。
我们也会一步一个脚印,争取每篇文章讲清讲透一件事,也希望大家阅读后有所收获,心情愉快。