一致性哈希

简单哈希 hash(object)%N 是最常用的算法，这种均衡性可能还行，但是稳定性比较差，不适用于分布式系统，因为分布式系统节点的增删是常见的需求，用这种简单的哈希算法来分布，在 N 变化的时候，会导致乾坤大挪移般的分布变化。

哈希算法本质是对一个固定输入产生固定输出的算法，最本质的可以先从两个方面衡量哈希算法的适用性：

平衡性：指哈希的结果能够尽可能分布到所有的节点的值域中，这样所有节点的值域都能得到利用（旁白：说白了，就是均衡喽，9个 key ，3个节点，最理想的就是每个节点处理3个）
单调性：指如果已经有一些内容通过哈希计算，分布到对应的节点中，当有新的节点加入系统时候，那么哈希的结果应能够保证原有已经分布的内容可以被映射到新的节点中去（或者在原地），而不会被映射到旧的节点；
这个是一个非常重要的考量，单机的简单哈希算法之所以不适用于分布式系统，就是因为这个单调性无法满足；

重点：单调性阐述的内容怎么理解呢？

增删节点都会导致新值域的产生，单调性说的就是：新值域要能从原有分布 key 里面分摊压力，原有值域却要尽量不落到原有已经分布的 key。

举个例子，假设有 key 集合：[ k1, k2, k3, k4, k5, k6, k7, k8, k9 ] ，有三个节点 [ A, B, C ] 。哈希分布之后 A [k1, k5, k8] ，B [ k2, k6, k9 ] ， C [ k3, k4, k7 ]。

场景：现在增加一个节点 D

单调性好的例子：增加节点后，导致分布变成：A [ k5, k8] ，B [ k2, k6, k9 ] ， C [ k3, k4 ] ，D [ k1, k7 ]。
我们看到 D 作为新加进来的节点，只是从 A，C 里面匀了一些 key 过来，原来 A，B，C 的内容全都不变，这就是一个单调性比较好的例子
单调性差的例子：如果说，因为加了一个 D 节点，变成：A [k2, k9，k8] ，B [ k4, k6 ] ， C [ k3, k5 ] ，D [ k1, k7 ]。这种结果看起来平衡性也不错，但是映射关系就有太多的变化，单调性太差了。这么大的映射变化，对应大分布式系统中，可能就是不能接受的数据迁移量；

一致性 hash —— 基础类型

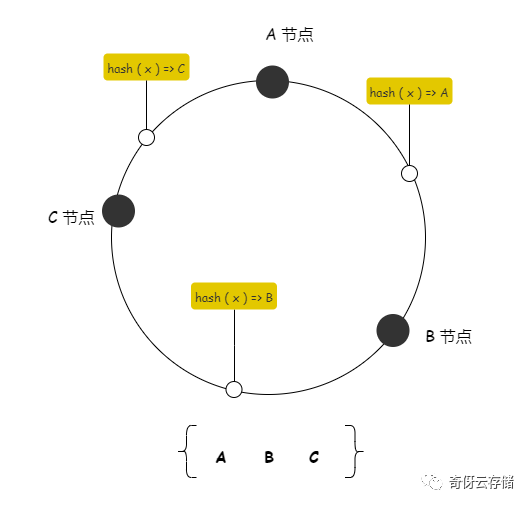
最基础的一致性 hash 算法就是把节点直接分布到环上，从而划分出值域， key 经过 hash( x ) 之后，落到不同的值域，则由对应的节点处理。类似下图，物理节点直接映射到环上：

最常见的值域空间大小是：2^32 - 1，节点落到这个空间，来划分不同节点所属的值域，现在我们举例就不搞这么大了，搞个简单的空间。

举一个例子，假设环的值域是 100（旁白：这个你自己随便定，反正就是一个边界值而已），A 的值域是 [ 0, 20 ) ，B 的值域是 [ 20, 70 ) ，C的值域是 [ 70, 100 )。（旁白：值域怎么来，A，B，C节点经过 hash 计算出一个 [0,100] 的值，落在环上，就会划分出两个区域）

上述基本的一致性哈希算法有明显的缺点：

1 . 随机分布节点的方式使得很难均匀的分布哈希值域（旁边：你看我黑圈圈在圆上的位置是不均衡的）；

2 . 在动态增加节点后，原先的分布就算均匀也很难再继续保证均匀；

3 . 增删节点带来的一个较为严重的缺点是：

a . 当一个节点异常时，该节点的压力全部转移到相邻的一个节点；

b . 当一个新节点加入时只能为一个相邻节点分摊压力；

一致性 hash —— 虚拟节点

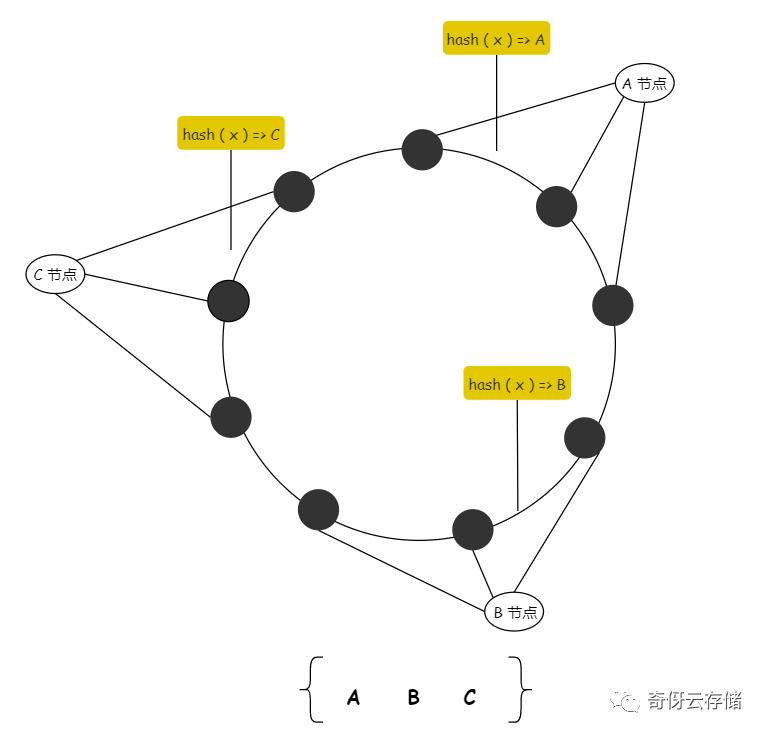
针对基础一致性 hash 的缺点一种改进算法是引入虚节点（virtual node）的概念。这个本质的改动：值域不再由物理节点划分，而是由固定的虚拟节点划分，这样值域的不均衡就不存在了。

步骤：

系统初始时就创建许多虚节点，虚节点的个数一般远大于未来集群中机器的个数，将虚节点均匀分布到一致性哈希值域环上，功能与基本一致性哈希算法中的节点相同；
为每个物理节点分配若干虚节点；
操作数据时，首先通过数据的哈希值在环上找到对应的虚节点，进而查找元数据找到对应的真实节点（旁白：所以这部分元数据是需要存下来的）；

使用虚节点改进有多个优点：

首先，一旦某个节点不可用，该节点将使得多个虚节点不可用，从而使得多个相邻的真实节点承载失效节点的压力；
同理，一旦加入一个新节点，可以分配多个虚节点，从而使得新节点可以负载多个原有节点的压力，从全局看，较容易实现扩容时的负载均衡；

那么我们最直观的想到这种样子：

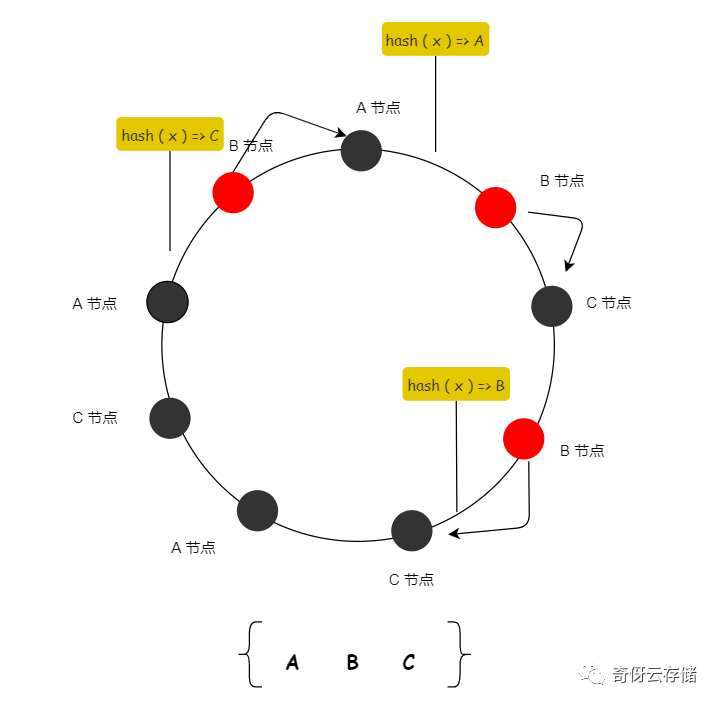
但其实这个还差点意思，就是虚拟节点和物理节点的绑定关系不能这样绑定，最好打散绑定。不然还是做不到上面说的两个优点，1）增节点的时候要能为多个节点分摊压力，2）删节点的时候要能让多个节点承担压力。

怎么打散？举一个简单交叉打散的例子：[A, B, C, B, C, A, C, A, B] （旁白：我这由于虚拟节点太少了，只能意思意思了，懂意思就行）

我标红的表示假设 B 节点故障，假设流量顺时针后移的话，那么就能用到 A，C 两个节点来分摊流量了，你看这样是不是就比之前要高级点。

由于有虚拟节点，所以可以保持值域不变，当出现增删节点只需要调整物理节点映射虚拟节点的关系即可，从而达到流量打散的目的。

Golang 实现

说了那么多，现在分析一个 golang 的一致性哈希的实现，非常有参考意义：

结构定义

首先，你需要一个抽象环（或者说序列的结构）。


type Hash func(data []byte) uint32
type Map struct {
    hash     Hash   // 计算 hash 的函数 
    replicas int    // 这个是副本数，这里影响到虚拟节点的个数
    keys     []int  // 有序的列表，从大到小排序的，这个很重要
    hashMap  map[int]string // 可以理解成用来记录虚拟节点和物理节点元数据关系的
}

举个例子，如果你有3个节点，replicas 设置成 3 ，那么就在环上有 9 个节点，9 个元素（后续就以此举例子）。

hash 环的初始化

然后你需要一个 New 的函数，把内存结构创建出来，初始化下，这个返回的你可以认为是一个空环：


func New(replicas int, fn Hash) *Map {
    m := &Map{
        replicas: replicas,
        hash:     fn,
        hashMap:  make(map[int]string),
    }
    if m.hash == nil {
        // 默认可以用 crc32 来计算hash值
        m.hash = crc32.ChecksumIEEE 
    }
    return m
}

hash 环添加节点

func (m *Map) Add(keys ...string) {
    // keys => [ A, B, C ]
    for _, key := range keys {
        for i := 0; i < m.replicas; i++ {
            // hash 值 = hash (i+key)
            hash := int(m.hash([]byte(strconv.Itoa(i) + key)))
            m.keys = append(m.keys, hash)
            // 虚拟节点 <-> 实际节点
            m.hashMap[hash] = key
        }
    }
    sort.Ints(m.keys)
}

比如，A，B，C 三个节点，replicas 为3，那么就：

节点输入：keys => [ A, B, C ]
用来计算 hash 值的输入是：i + key，也就是输入为：[ 0A, 1A, 2A, 0B, 1B, 2B, 0C, 1C, 2C] ；
计算出来的 hash 序列是：m.keys = [ hash(0A), hash(1A), hash(2A), hash(0B), hash(1B), hash(2B), hash(0C), hash(1C), hash(2C) ] ；
我们认为 hash 函数是有比较好的平衡性的，那么计算出的值，应该就是随机均衡打散的，我们认为是符合概率分布的；
最后会把这个 hash 值的序列做一个排序，做完排序之后，其实就完成了值域的打散划分；

一致性 hash 请求

func (m *Map) Get(key string) string {
    if m.IsEmpty() {
        return ""
    }
    // 根据用户输入key值，计算出一个hash值
    hash := int(m.hash([]byte(key)))
    // 查看值落到哪个值域范围？选择到虚节点
    idx := sort.Search(len(m.keys), func(i int) bool { return m.keys[i] >= hash })
    if idx == len(m.keys) {
        idx = 0
    }
    // 选择到对应物理节点
    return m.hashMap[m.keys[idx]]
}

以上就是一个完整的一致性hash的实现了，是不是特别简单，这个实现就能适用于我们常用的分布式缓存的。

分布式系统基石之一（一致性 hash 算法）