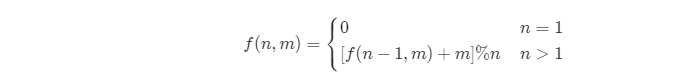吊打剑指offer,一道腾讯面试题,面试官直呼小夕NBPLUS
阅读须知
小夕:共2种解法,新解法在后文,为了进行连续,把之前的解法也重新发了一遍。
题目
0,1,···,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
输入: n = 5, m = 3 输出: 3 示例 2:
输入: n = 10, m = 17 输出: 2
限制:
1 <= n <= 10^5 1 <= m <= 10^6
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
假设数组为0,1,2,3,4,5,6, 也就是n = 7 每次我们要删除第 m 个数字 其中 m = 3。
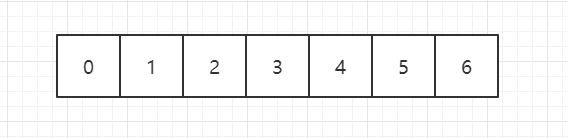
删除位置的下标 newIdx 和起始 idx的下标之间的关系newIdx = idx + m -1
删除完以后:
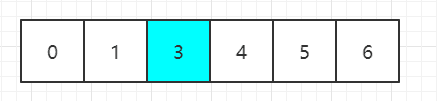
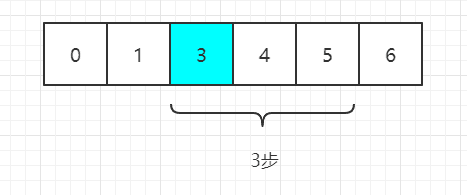
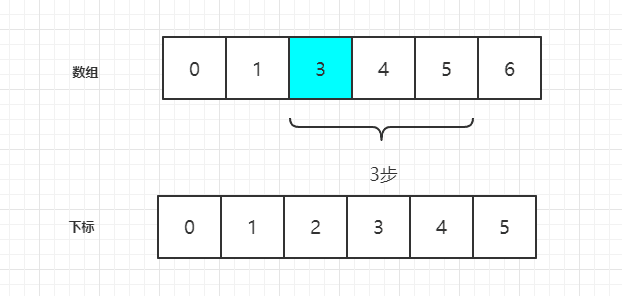
idx=3,那么数字 5 记录为 newIdx。
newIdx = idx + m -1
到这里,明显可以看出来,下一个要删除的数字的下标是 idx = idx + m -1 我们一直去删除就行。
上述5删除以后:
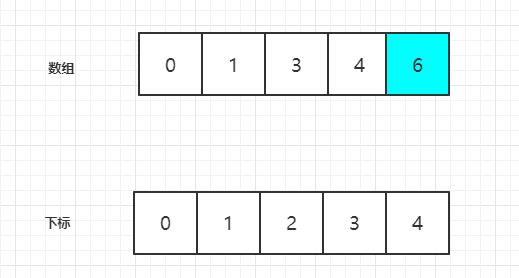



6 0 1 所以下次要删除的数字的下标是1.
按照我们之前的结论idx = idx + m -1
idx = 4 + 3 -1 = 6
而要删除的数字是 1,下标也是1.那么 6 不等于1啊,那这里该怎么进行转换呢?
当前数组的总数是 n = 5。由于数到末尾会从头继续数,所以最后取模一下 6%5 = 1.
因此得出最后的公式是:idx = (idx + m - 1) % n
idx 是要删除的数组中的数字的下标。
每次都删除这个下标,然后直到数组中只剩下一个数字,那么就结束循环。返回这个数字。
代码
Java
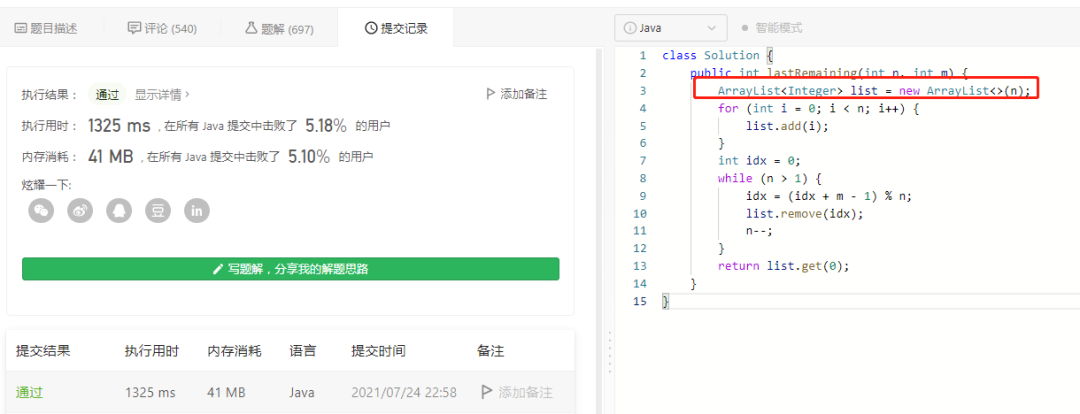
class Solution {
public int lastRemaining(int n, int m) {
ArrayList<Integer> list = new ArrayList<>(n);
for (int i = 0; i < n; i++) {
list.add(i);
}
int idx = 0;
while (n > 1) {
idx = (idx + m - 1) % n;
list.remove(idx);
n--;
}
return list.get(0);
}
}
ArrayList 中查找元素的时间复杂度是O(1),但是删除1个元素的话,时间复杂度是O(n);·LinkedList`中查找元素的时间复杂度是O(n),但是删除1个元素的,时间复杂度是O(1)。
按理说,这两个用哪个都可以,但是LinkedList超时了:
ArrayList 反而没有问题。
那么小夕去看了LinkedList源码:
源码分析,LinkedList是去遍历链表找到以后删除元素。
小夕去看了ArrayList源码:
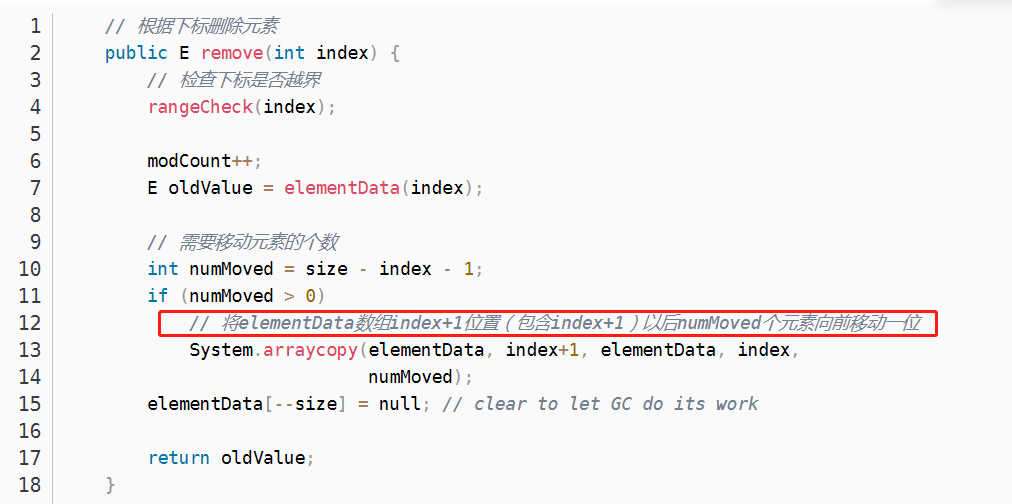
源码分析:将elementData数组index+1位置(包含index+1)以后numMoved个元素向前移动一位。
小夕分析:
数组中的删除,数组在内存中是连续的内存地址存储的。删除起来,是找下一个元素,把下一个元素复制到上一个被删除的位置,它们在内存中是紧密挨着的,这样在进行数组复制的时候,找下一个元素的位置的时间很短。
链表中的删除:
由于链表中元素在内存中不是连续的,所以从上一个元素0开始找下一个元素1,在内存中寻找元素1的位置的时间花销大。

而在LinkedList中从1去寻址找到2,链表是无序存放的,所以链表中的1和2在内存中的距离很远,寻址时间长。



图解例子
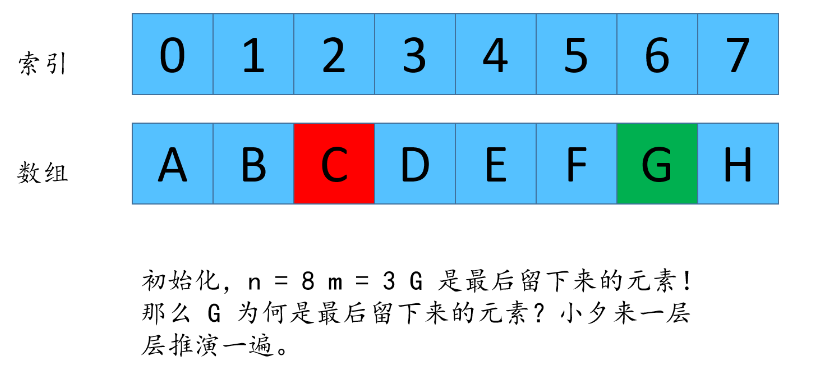
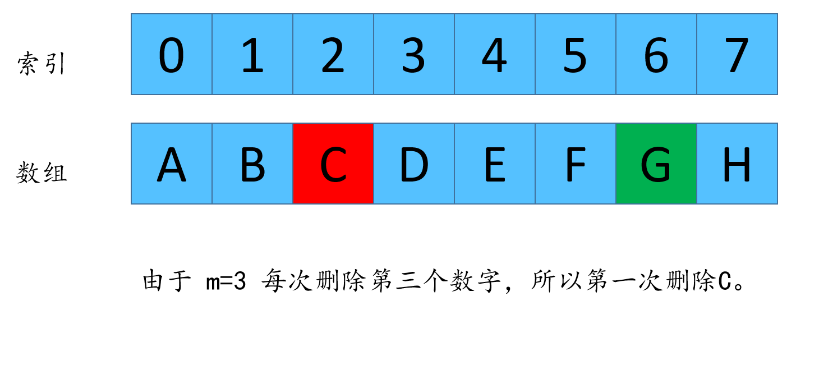

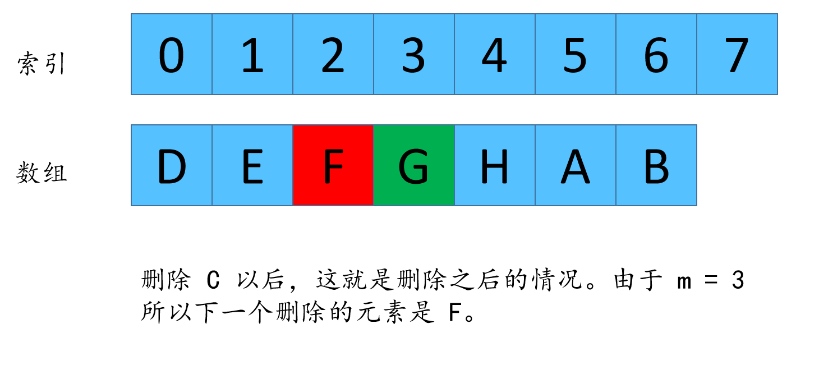
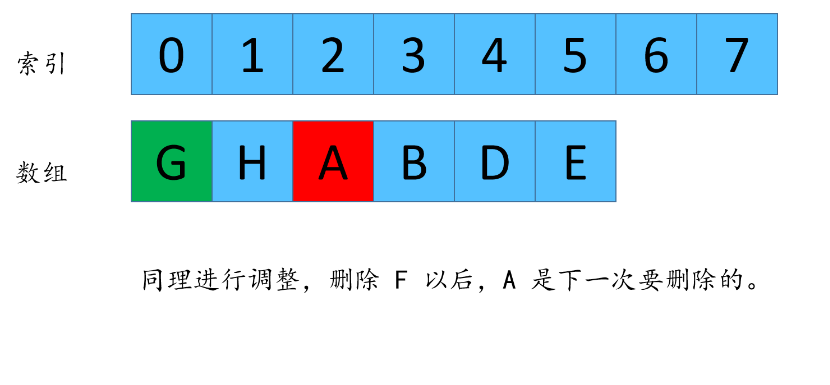
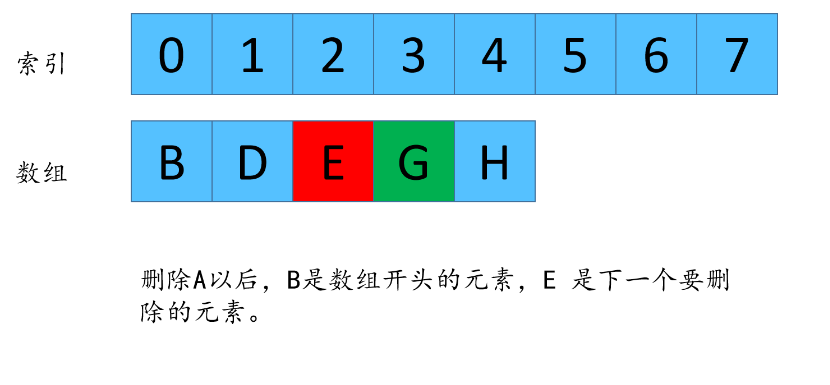
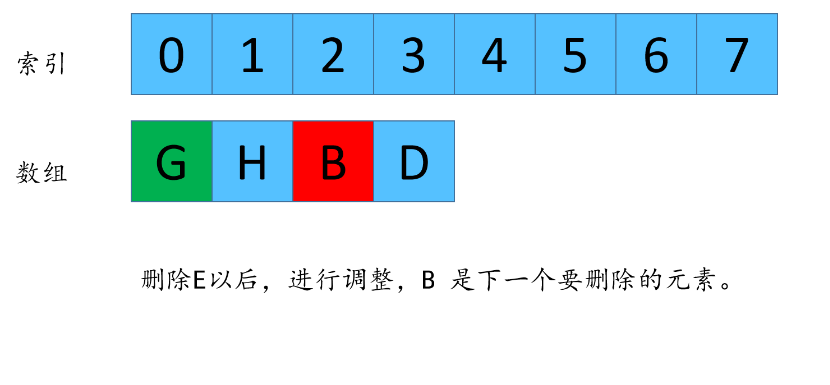
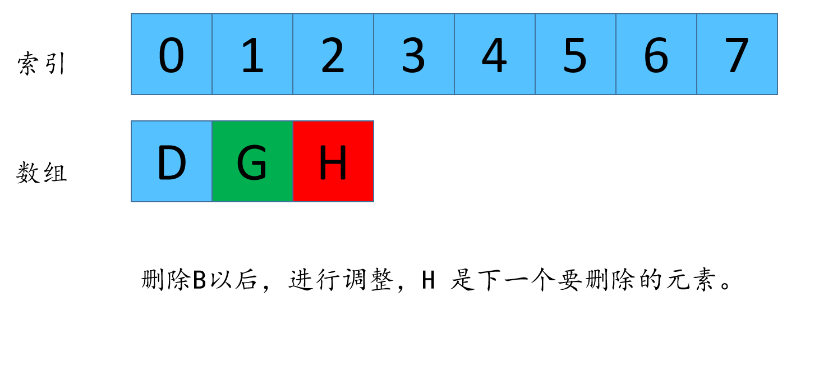
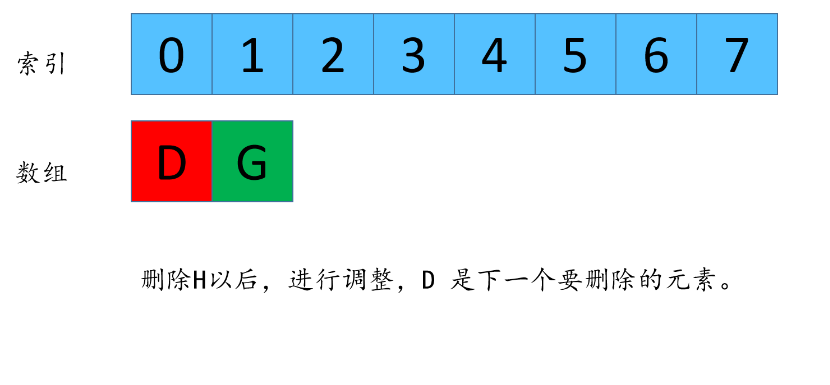
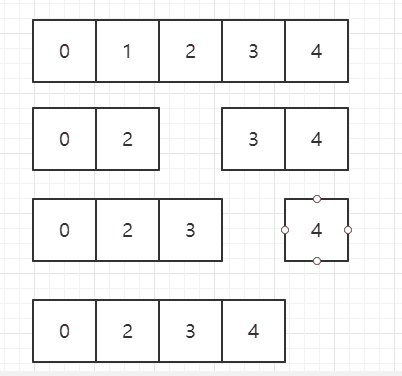
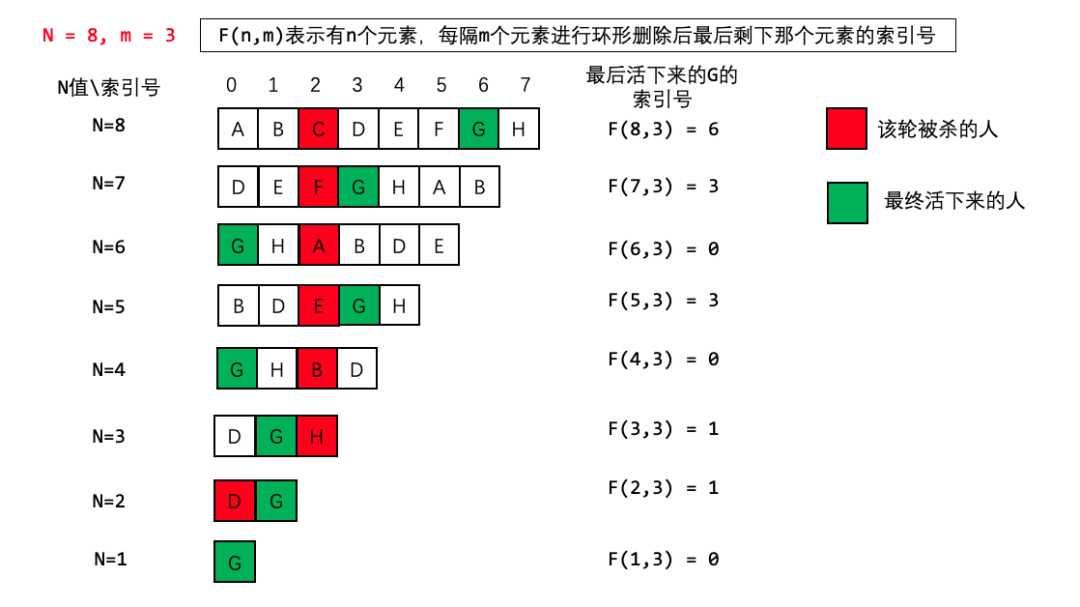
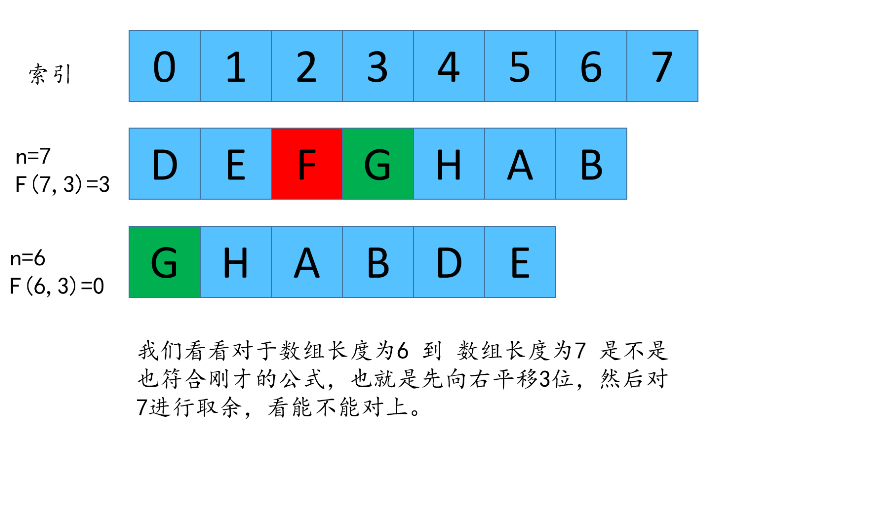
由于数组每次都删除元素,所以G的下标在n不同的时候,值也是不同的,我现在来找一下,n 和 n -1 剩下来的G的下标之间的关系。
在刚才举的那个例子中 n = 8 m = 3,
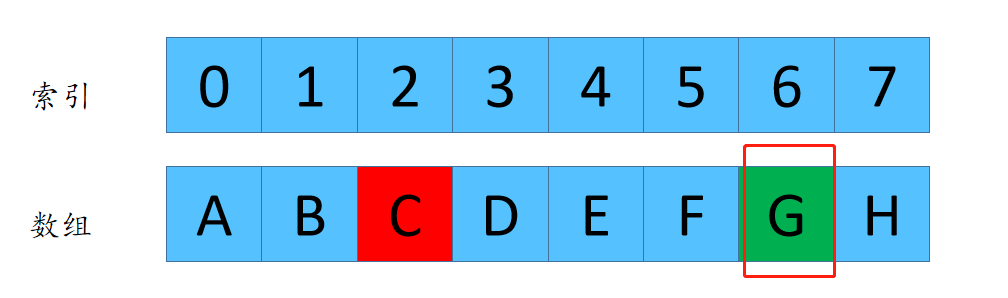
F(8,3) = 6 这个代表着数组长度为8,每次删除第3个数字,最后剩下来的是元素G的下标是6(为啥是G,因为小夕刚才演示了一遍,每次删除第三个元素,最后剩下的是 G,所以每次我们只需要关注G的元素的下标).
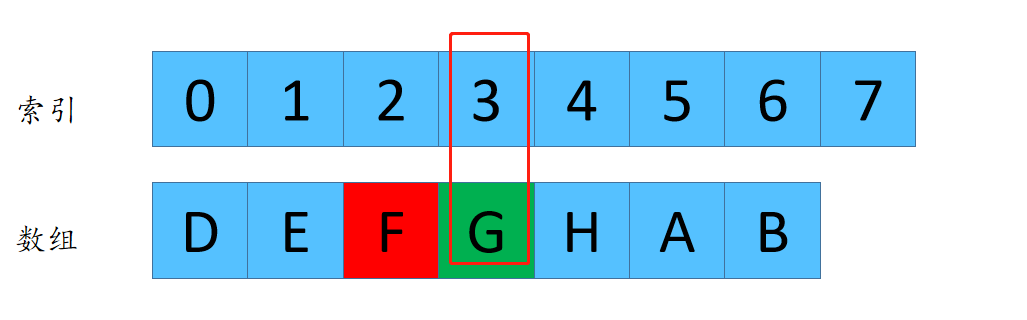
F(7,3) =3 这个代表着数组长度为7,每次删除第3个数字,最后剩下来的是元素G的下标是3(为啥是G,因为小夕刚才演示了一遍,每次删除第三个元素,最后剩下的是 G,所以每次我们只需要关注G的元素的下标).
F(6,3) =0 这个代表着数组长度为6,每次删除第3个数字,最后剩下来的是元素G的下标是0.
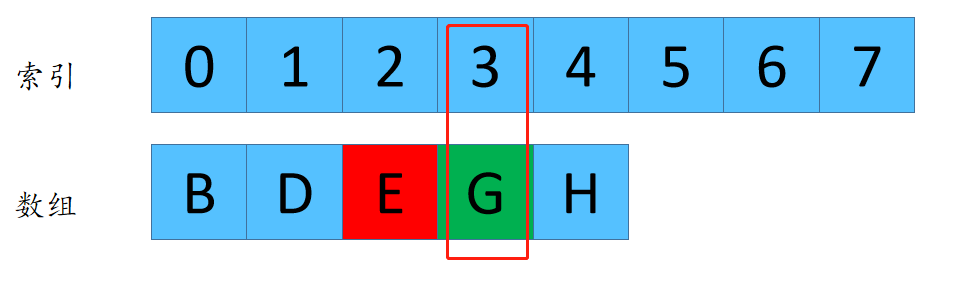
F(5,3) =3 这个代表着数组长度为5,每次删除第3个数字,最后剩下来的是元素G的下标是3.
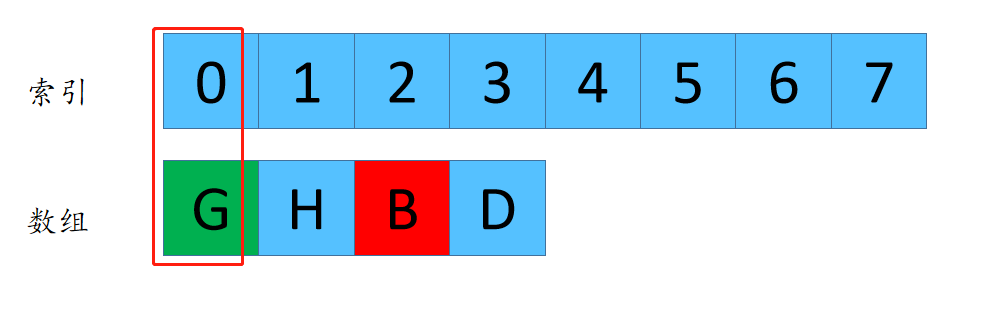
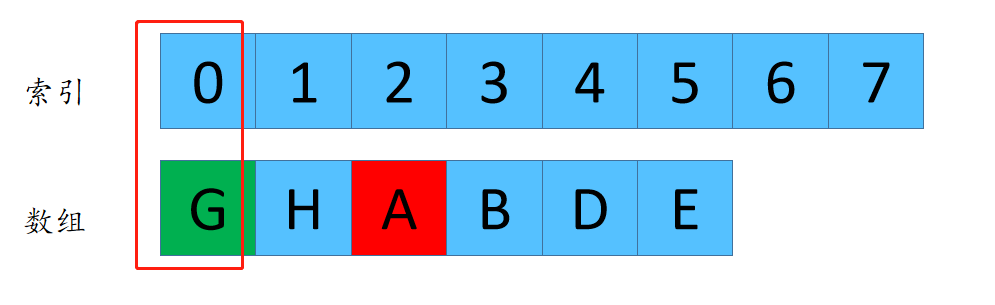
F(4,3) =0 这个代表着数组长度为4,每次删除第3个数字,最后剩下来的是元素G的下标是0.
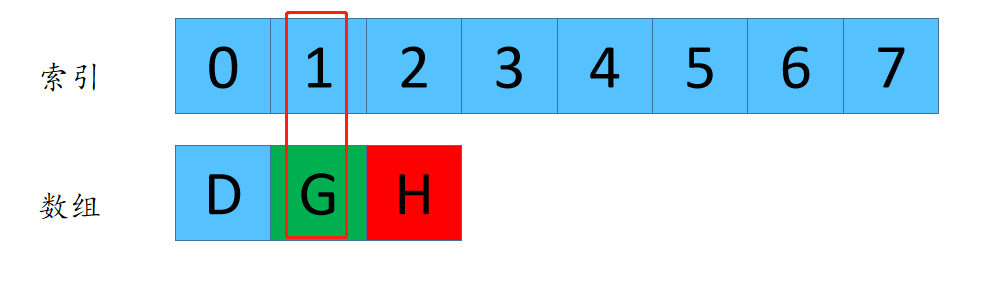
F(3,3) = 1 这个代表着数组长度为3,每次删除第3个数字,最后剩下来的是元素G的下标是1.
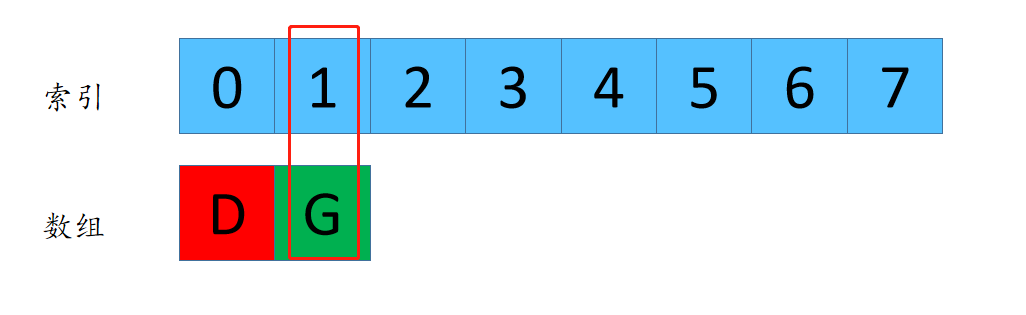
F(2,3) = 1 这个代表着数组长度为2,每次删除第3个数字,最后剩下来的是元素G的下标是1.
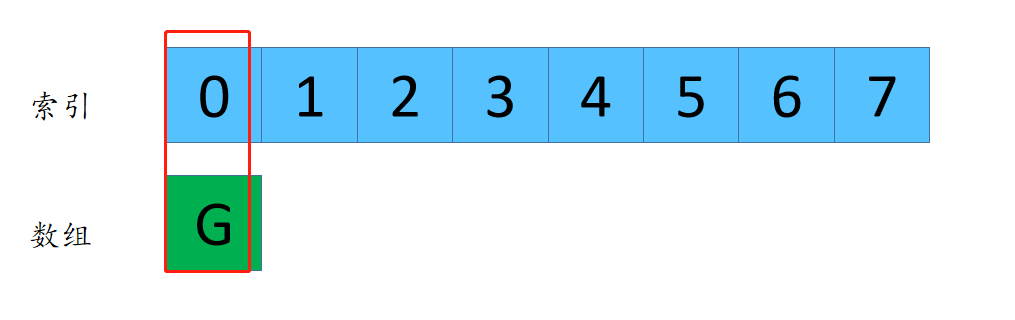
F(1,3) = 0 这个代表着数组长度为1,每次删除第3个数字,由于当数组长度为1的时候,题目说了圆圈里剩下的最后一个数字结束删除,所以当数组长度为1的时候,不进行删除,这个圆圈最后剩下的数字就是这个唯一的一个元素,这个元素的下标必然是0。
把上面的结果汇总一下。下图:https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/huan-ge-jiao-du-ju-li-jie-jue-yue-se-fu-huan-by-as/
进行反推。
- 现在是已知 F(1,3)= 0 如何反推出
F(2,3)、F(3,3),F(4,3),F(5,3),F(6,3),F(7,3)、F(8,3)
我们先看一下,如何从F(7,3)反推出F(8,3)


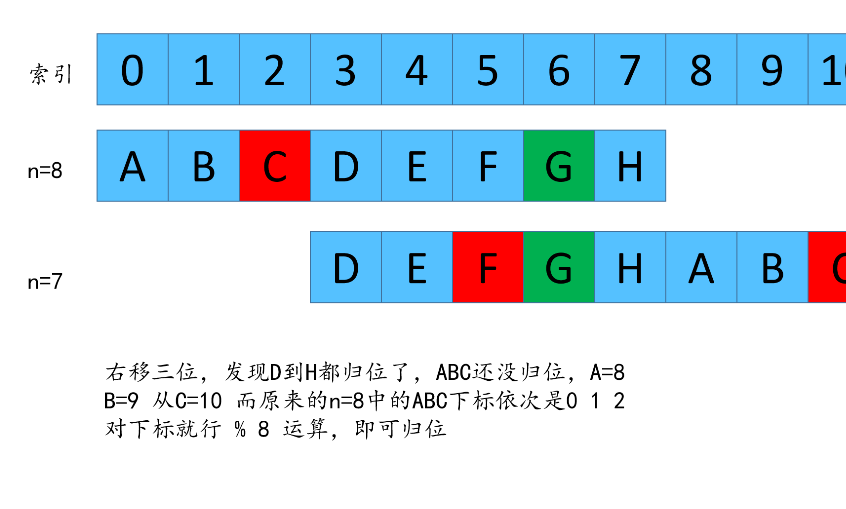
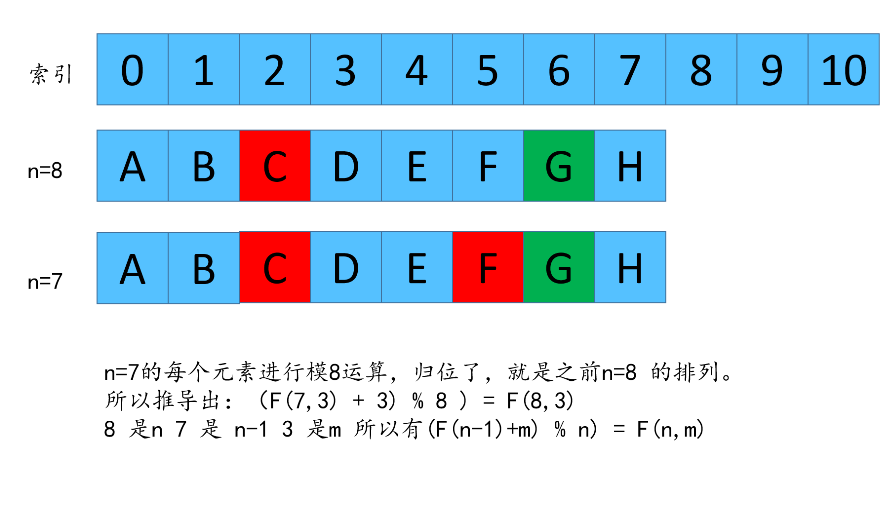
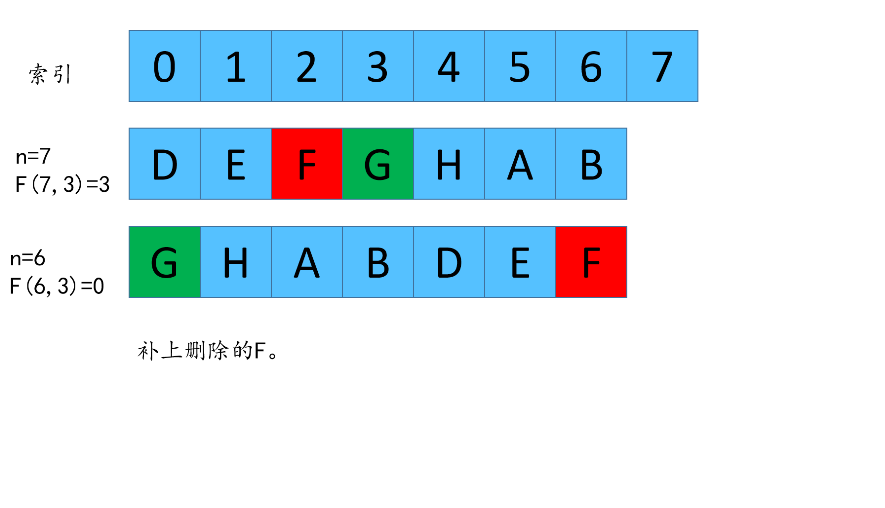
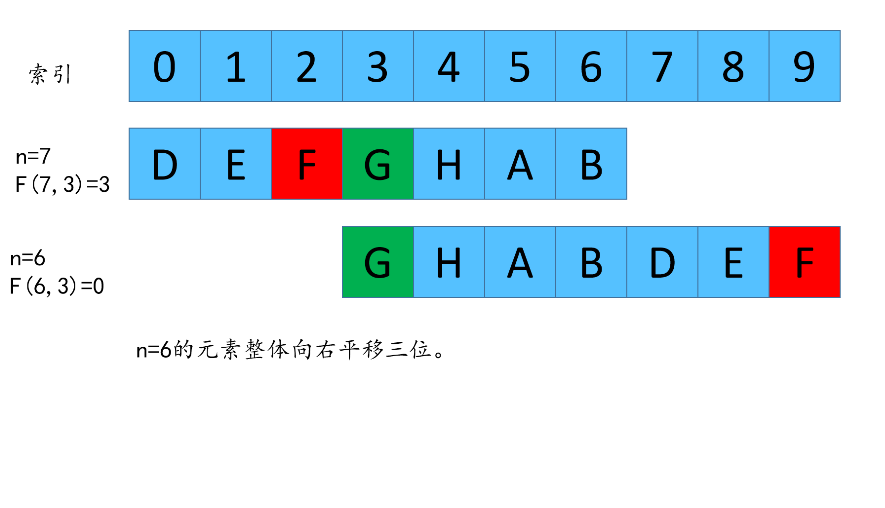
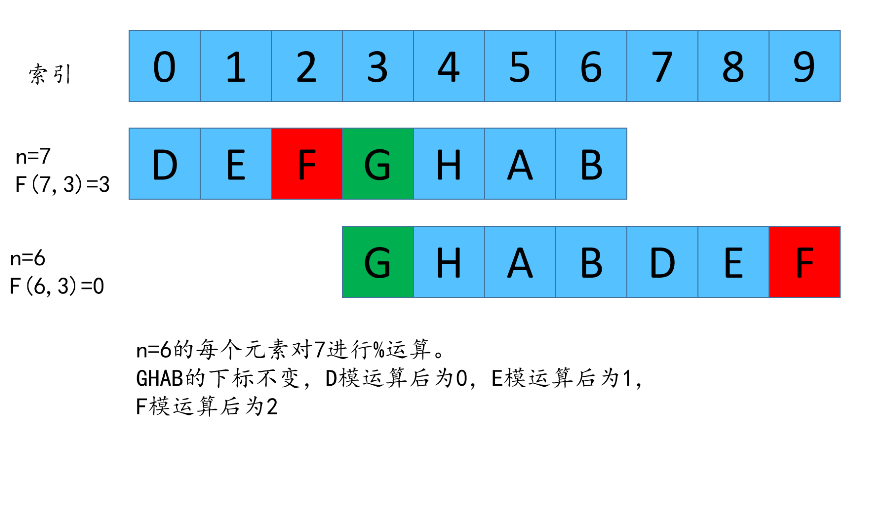
总结递推公式
我们这里反推出了公式,由于 f(1,m) = 0 代表数组中只有一个元素,那么这个剩下的数字的下标必然是 0.
因此有:
代码
Java
class Solution {
public int lastRemaining(int n, int m) {
int f = 0;
for (int i = 2; i != n + 1; ++i) {
f = (m + f) % i;
}
return f;
}
}
C++
class Solution {
public:
int lastRemaining(int n, int m) {
int pos = 0; // 最终活下来那个人的初始位置
for(int i = 2; i <= n; i++){
pos = (pos + m) % i; // 每次循环右移
}
return pos;
}
};JS
/**
* @param {number} n
* @param {number} m
* @return {number}
*/
var lastRemaining = function(n, m) {
/*
约瑟夫环 正向递归 |逆向迭代
因为是从数字0开始 故 索引和数组值是一直的 nums[i] = i
1. 逆向思维 遍历迭代 最后肯定是只剩下一个人 且 此时的索引为0 故从倒数第二轮反推
2. 正向递归 终止条件为 n = 1 即数组中只剩下一个人返回此时索引 0
(当前index + m) % 上一轮剩余数字的个数
关键代码:当前轮最后剩下的数字 = (上一轮剩下的数字索引 + 计数的距离m) %(模上)当前数组/圆圈长度l
推到公式
fn(n, m) = n === 1 ? 0 : (fn(n - 1, m) + m) % n
i为最终轮时 幸存数所在数组内的索引
*/
let i = 0
for (let l = 2; l <= n; l++) i = (i + m) % l
return i
// 2. 递归实现 当数组中长度大于等于2时 继续递归下去 直到n = 1
return n > 0 ? (lastRemaining(n - 1, m) + m) % n : 0
};
Python
class Solution:
def lastRemaining(self, n: int, m: int) -> int:
x = 0
for i in range(2 , n+1):
x = (x + m) % i
return x