动态规划解分割回文串
问题描述
来源:LeetCode第1278题
难度:困难
给你一个由小写字母组成的字符串s,和一个整数k。
请你按下面的要求分割字符串:
- 首先,你可以将s中的部分字符修改为其他的小写英文字母。
- 接着,你需要把s分割成k个非空且不相交的子串,并且每个子串都是回文串。
请返回以这种方式分割字符串所需修改的最少字符数。
示例 1:
输入:s = "abc", k = 2
输出:1
解释:你可以把字符串分割成 "ab" 和 "c",并修改 "ab" 中的 1 个字符,将它变成回文串。
示例 2:
输入:s = "aabbc", k = 3
输出:0
解释:你可以把字符串分割成 "aa"、"bb" 和 "c",它们都是回文串。
示例 3:
输入:s = "leetcode", k = 8
输出:0
提示:
- 1 <= k <= s.length <= 100
- s 中只含有小写英文字母。
动态规划解决
这题是让通过修改一些字符把字符串分割为k个子串,并且每个子串都是回文的,问最少修改的字符数。
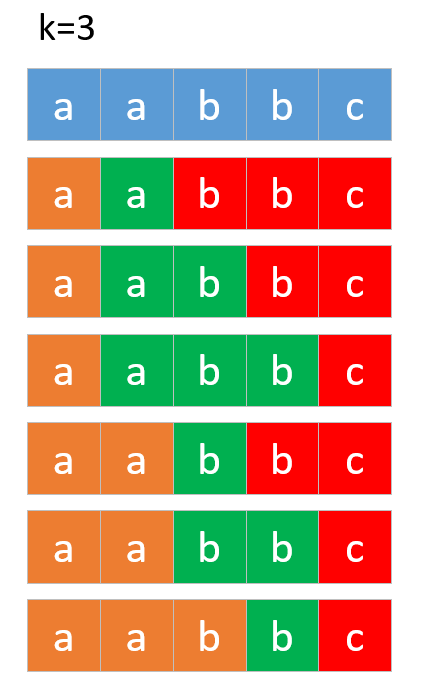
最容易想到的就是把字符串s分割k个子串的所有可能组合,然后计算每个组合中子串变成回文串修改字符的数量,最后返回最小的即可。比如示例二中我们可以分割为
但是当字符串s比较长的时候,运行效率是很差的。这里我们可以使用动态规划来解决,定义dp[i][j]表示表示字符串s的前i个字符分割为j个子串的修改的最小字符数。很明显i必须大于等于j,要不然不可能分割为j个子串。
动态规划最关键的是找出递推公式,当我们要求dp[i][j]的时候,只需要找出前m个字符分割成j-1个子串所修改的最小字符数+最后一个子串所需要修改字符数。(最后一个子串就是前i个字符-前m个字符),看到这里大家是不是很容易想到比较经典的基础背包问题,前面有讲过背包问题,其中还有多重背包和完全背包这些我们以后会再讲。
所以递推公式我们很容易想到
dp[i][j]=dp[m][j-1]+change(s,m,i-1);
这里我们需要枚举m的值,但要注意m必须大于等于j-1,如下图所示
这题要求的是返回最小的字符修改数,所以我们记录最小的即可
dp[i][j] = Math.min(dp[i][j], dp[m][j - 1] + change(s, m, i - 1));
其中change(s,m,i-1)表示字符串s[m,i-1]变成回文串所需要修改的字符数。他的代码比较简单,我们来看下
1//字符串的子串[left,right]变成回文串所需要修改的字符数
2private int change(String s, int left, int right) {
3 int count = 0;
4 while (left < right) {
5 //如果两个指针指向的字符相同,我们不需要修改。
6 //如果不相同,只需要修改其中的一个即可,所以
7 // 修改数要加1
8 if (s.charAt(left++) != s.charAt(right--))
9 count++;
10 }
11 return count;
12}分析到这里,这题的代码基本上就呼之欲出了,我们来看下完整代码
1public int palindromePartition(String s, int k) {
2 int length = s.length();
3 //dp[i][j]表示s的前i个字符分割成k个子串所修改的最少字符数。
4 int[][] dp = new int[length + 1][k + 1];
5 //因为这题要求的是所需要修改的最少字符数,初始值我们赋值尽可能大
6 for (int i = 0; i < dp.length; i++) {
7 Arrays.fill(dp[i], length);
8 }
9 //前i个字符,分割成j个回文子串
10 for (int i = 1; i <= length; i++) {
11 //前i个字符最大只能分割成i个子串,所以不能超过i,
12 //我们取i和k的最小值
13 int len = Math.min(i, k);
14 for (int j = 1; j <= len; j++) {
15 if (j == 1) {
16 //如果j等于1,则表示没有分割,我们直接计算
17 dp[i][j] = change(s, j - 1, i - 1);
18 } else {
19 //如果j不等于1,我们计算分割所需要修改的最小字符数,因为m的值要
20 //大于等于j-1,我们就从最小的开始枚举
21 for (int m = j - 1; m < i; m++) {
22 //递推公式
23 dp[i][j] = Math.min(dp[i][j], dp[m][j - 1] + change(s, m, i - 1));
24 }
25 }
26 }
27 }
28 //返回前length个字符分割成k个子串所需要修改的最少字符数
29 return dp[length][k];
30}
31
32//字符串的子串[left,right]变成回文串所需要修改的字符数
33private int change(String s, int left, int right) {
34 int count = 0;
35 while (left < right) {
36 //如果两个指针指向的字符相同,我们不需要修改。
37 //如果不相同,只需要修改其中的一个即可,所以
38 // 修改数要加1
39 if (s.charAt(left++) != s.charAt(right--))
40 count++;
41 }
42 return count;
43}动态规划代码优化
上面代码中都有注释,这里就不在过多介绍,我们来看一下change方法,因为这里会涉及到字符的重复计算,导致效率不高,我们可以先计算所有的子串变成回文串需要修改的字符数,然后再使用,来看下代码
1public int palindromePartition(String s, int k) {
2 int length = s.length();
3
4 //palindrome[i][j]表示子串[i,j]转化为回文串所需要的修改的字符数
5 int[][] palindrome = new int[length][length];
6 //2种实现方式
7 // //一列一列的从左往右(只遍历右上部分)
8 // for (int j = 1; j < length; j++) {
9 // for (int i = 0; i < j; i++) {
10 // palindrome[i][j] = palindrome[i + 1][j - 1] + (s.charAt(i) == s.charAt(j) ? 0 : 1);
11 // }
12 // }
13
14 //一行一行的从下往上(只遍历右上部分)
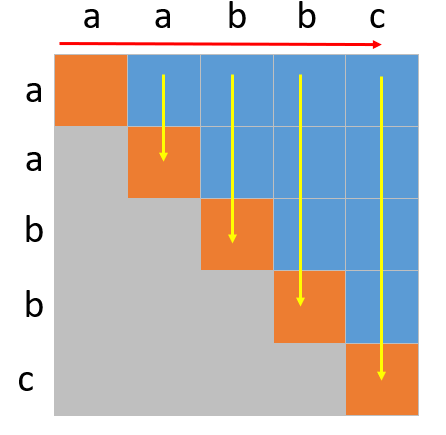
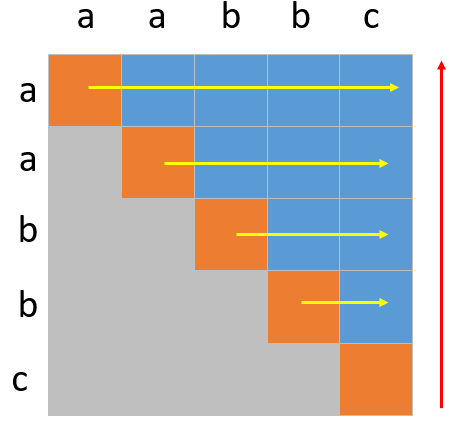
15 for (int i = length - 2; i >= 0; i--) {
16 for (int j = i + 1; j < length; j++) {
17 palindrome[i][j] = palindrome[i + 1][j - 1] + (s.charAt(i) == s.charAt(j) ? 0 : 1);
18 }
19 }
20
21 //dp[i][j]表示s的前i个字符分割成k个回文子串的最少次数,
22 //第一行和第一列应该都是0。
23 int[][] dp = new int[length + 1][k + 1];
24 for (int i = 1; i < dp.length; i++) {
25 Arrays.fill(dp[i], Integer.MAX_VALUE);
26 }
27 //前i个字符,分割成j个回文子串
28 for (int i = 1; i <= length; i++) {
29 int len = Math.min(i, k);
30 for (int j = 1; j <= len; j++) {
31 if (j == 1)//字符串的下标是从0开始的,所以这里要减1
32 dp[i][j] = palindrome[j - 1][i - 1];
33 else
34 for (int m = j - 1; m < i; m++) {
35 dp[i][j] = Math.min(dp[i][j], dp[m][j - 1] + palindrome[m][i - 1]);
36 }
37 }
38 }
39 return dp[length][k];
40}因为dp[i][j]中i必须大于等于j,所以这里遍历的时候可以有两种方式,如下图所示