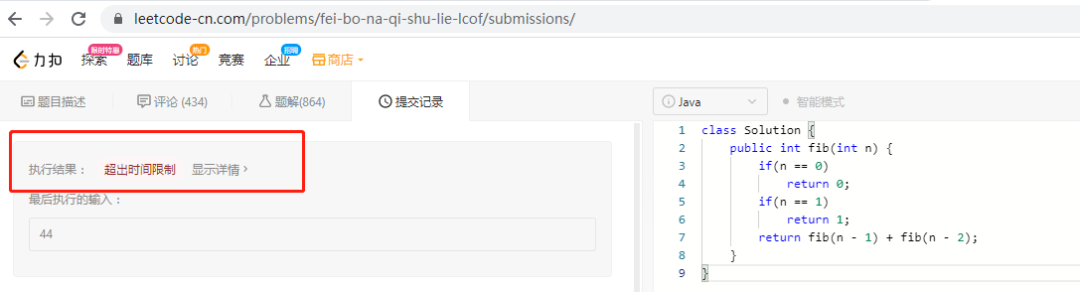
字节面试题太坑了，刚回答完，就被面试官diss了！

题目

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/fei-bo-na-qi-shu-lie-lcof

面试现场

class Solution {
    public int fib(int n) {
        if(n == 0)
            return 0;
        if(n == 1)
            return 1;
        return fib(n - 1) + fib(n - 2);
    }
}

回到学校

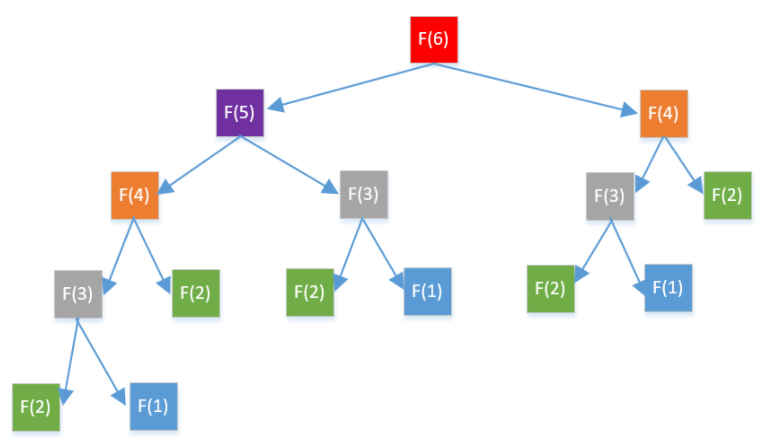
比如计算fib(6)，从图片中可以看到，f(3)重复计算了3次，f(4)重复计算了2次，可想而知，越往上，那么重复计算的次数会越多。

记忆法递归

class Solution {
    public int fib(int n) {
        int [] arr = new int[n + 1];
        for (int i = 0; i < arr.length;i++) {
            arr[i] = -1;
        }
        return fibWithArray(n, arr);
    }
    public int fibWithArray(int n,int [] arr) {
        if (n < 2) {
            return n;
        }
        if (arr[n] == -1) {
            arr[n] = (fibWithArray(n-1, arr) + fibWithArray(n-2, arr)) % 1000000007;
        }
        return  arr[n];
    }
}

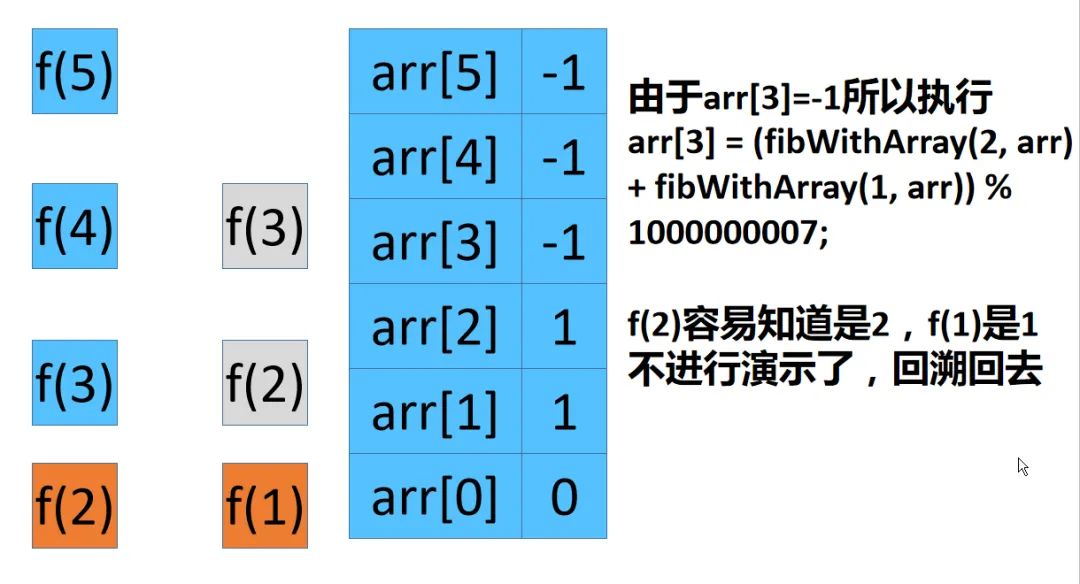
小夕：之前我的递归因为存在重复计算的问题，所以我就新开了一个数组，并初始化这个数组都为-1，当这个数组中的值对应是-1呢，那么就执行arr[n] = (fibWithArray(n-1, arr) + fibWithArray(n-2, arr)) % 1000000007;，执行完以后arr[n]就不是-1了，那么下次因为不是-1.所以这个if (arr[n] == -1)判断条件就不满足，所以就直接返回了arr[n]，不会存在重复计算的问题！

举个例子，比如计算f(5) 从之前的图中可以看出来，为了计算f(5) 那么f(3)需要计算两次。

这里小夕我举个例子就一目了然了。现在用了数组只需要一次。

记忆法递归例子

递归动画

斐波那契树之前的递归.gif

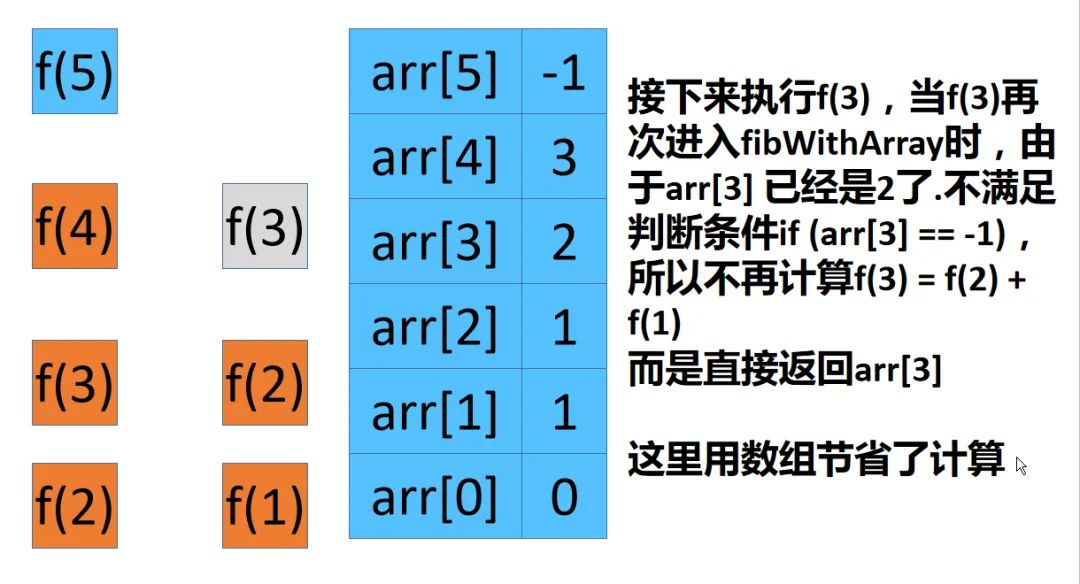
小夕：所以可以看到，因为有了数组，让计算f(5)的时候，f(4)f(3)f(2)只计算了一次，也就是说计算f(n)的时候，f(1)到f(n-1)只计算了一次，大大的减少了递归的时间。

动态规划解法

小管助教：小夕你的，"记忆化递归"的思考路径是"自顶向下"。而“动态规划”思考问题路径是"自下而上"。实际上，先“真正地”解决了数据规模较小的问题，然后一步一步地解决了数据规模较大的问题。

而斐波那契数列是通过"递归"定义的，通过这个递归关系式，我们可以知道斐波那契数列中任意一个位置的数值。

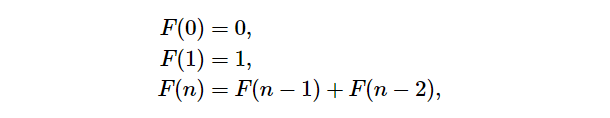
动态规划的关键是要找出来转移方程，什么是状态转移方程？你把 f(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态n - 2 相加转移而来，这就叫状态转移。

所以很容易从斐波那契数列中得到状态转移方程：dp[i+1] = dp[i] + dp[i−1]状态转移方程的初始状态很容易知道是:dp[0] = 1 dp[1] = 1,我们要求的第n个斐波那契数列就是dp[n]所以根据转移方程，可以得到如下代码：

class Solution {
    public int fib(int n) {
        if(n < 2)
            return n;
        int dp[] = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for(int i=2;i<=n;i++){
            dp[i] = (dp[i-1] + dp[i-2]) % 1000000007;
        }
        return dp[n];
    }
}

动态规划优化

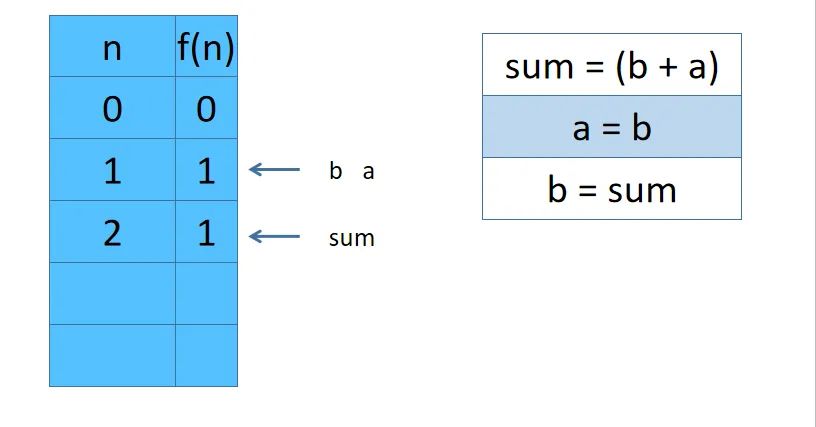
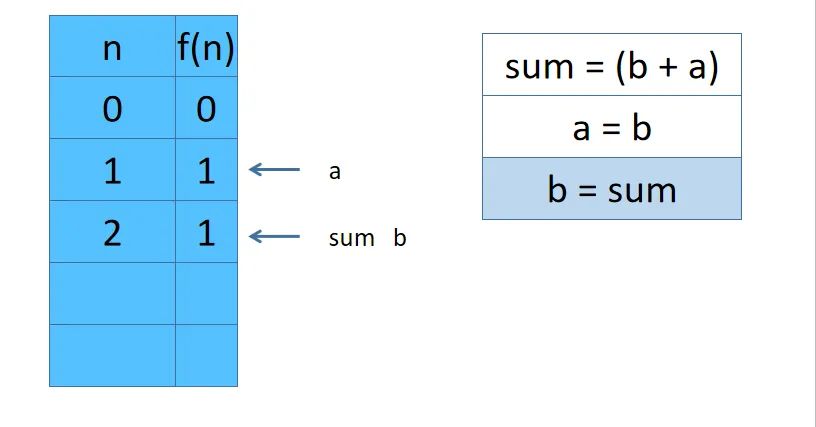
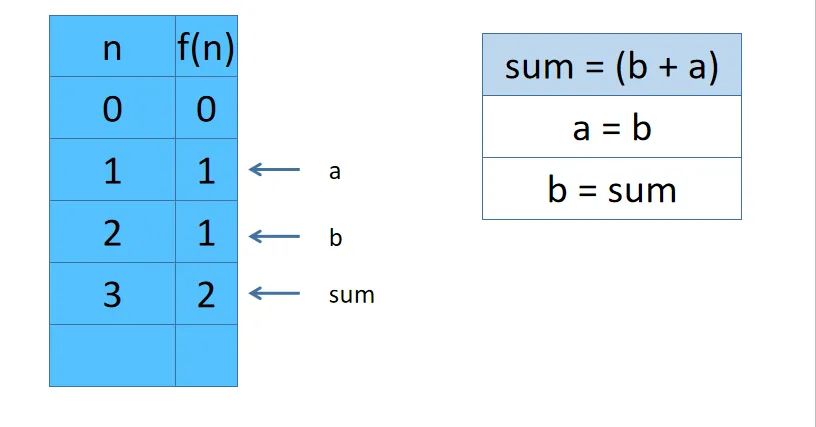
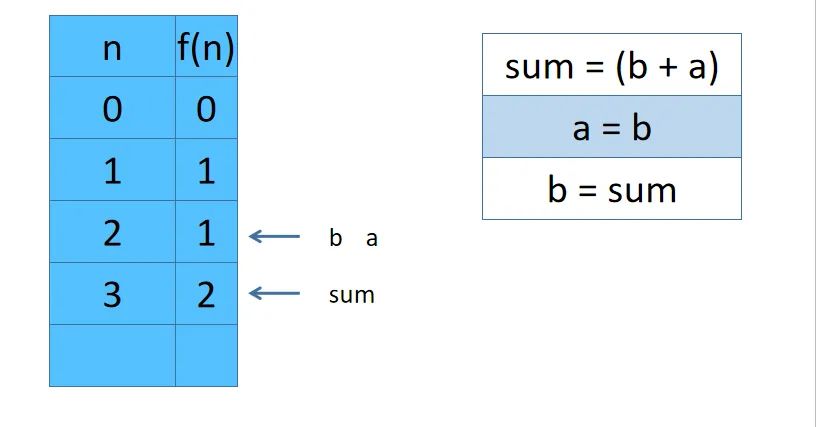
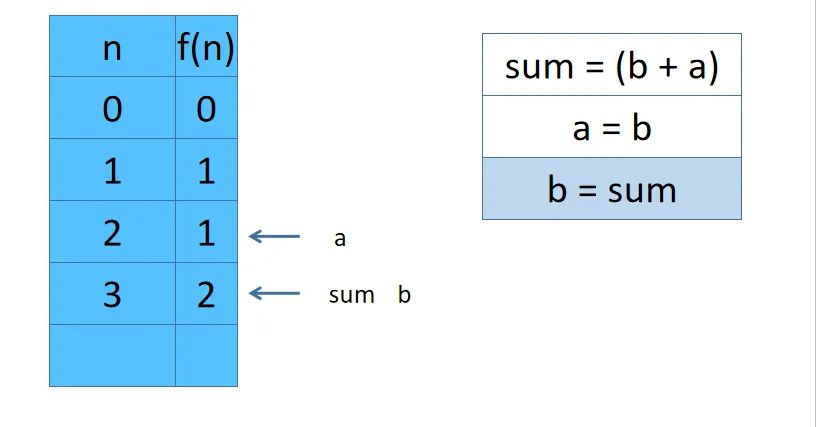
小管助教：由于dp数组中我们需要的数只和 dp[i] dp[i-1] dp[i-2]有关，所以可以用sum,b,a来分别代表dp[i] dp[i-1] dp[i-2]。

• 比如为了计算 dp[3], 需要先计算dp[2] = dp[1] + dp[0]。我们不使用数组，也就是sum = b + a。此时 sum =1 b = 1 a= 0
• 为了计算dp[3] 需要保留dp[2]也就是sum的计算结果。
• 于是我们让a = b = 1 也就是让a 保留 dp[1]的结果 让b = sum = 1也就是让b保留dp[2]的结果
• 所以dp[3] = b + a = 2

上几个图示例一下。

动画演示一下

斐波那契.gif

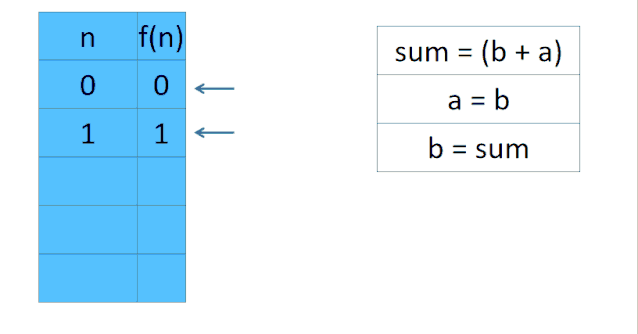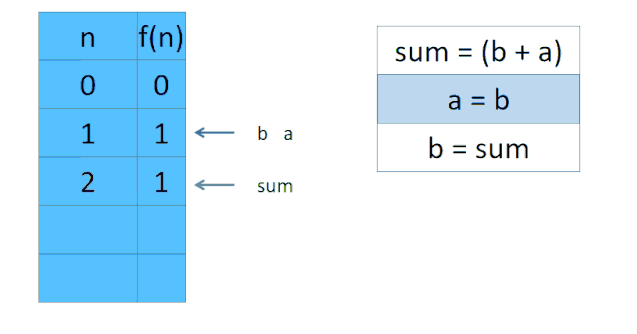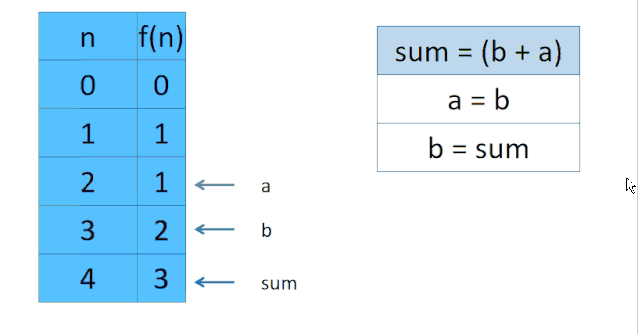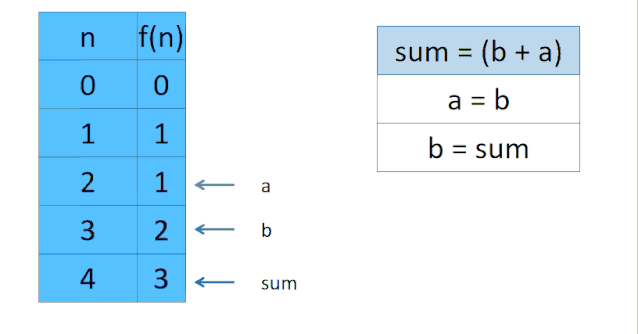
复杂度

由于没使用数组，空间复杂度是O(1)，时间复杂度是O(n)

Java解法

class Solution {
    public int fib(int n) {
        int a = 0;
        int b = 1;
        if(n == 0)
            return 0;
        if(n == 1)
            return 1;
        int i = 2;
        int sum=0;
        while(i <= n)
        {
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
            i++;
        }
        return sum;
    }
}

C++解法

class Solution {
public:
    int fib(int n) {
        int a = 0;
        int b = 1;
        if(n == 0)
            return 0;
        if(n == 1)
            return 1;
        int i = 2;
        int sum=0;
        while(i <= n)
        {
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
            i++;
        }
        return sum;

    }
};

JS解法

/**
 * @param {number} n
 * @return {number}
 */
var fib = function(n) {
    var a = 0;
    var b = 1;
    if(n == 0)
        return 0;
    if(n == 1)
        return 1;
    var i = 2;
    var sum=0;
    while(i <= n)
    {
        sum = (a + b) % 1000000007;
        a = b % 1000000007;
        b = sum;
        i++;
    }
    return sum;
};

PY解法

class Solution(object):
    def fib(self, n):
        a = 0;
        b = 1;
        if(n == 0):
            return 0;
        if(n == 1):
            return 1;
        i = 2;
        sum=0;
        while(i <= n):
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
            i += 1;
        return sum;

PHP解法

class Solution {

    /**
     * @param Integer $n
     * @return Integer
     */
    function fib($n) {
        $a = 0;
        $b = 1;
        if($n == 0)
            return 0;
        if($n == 1)
            return 1;
        $i = 2;
        $sum=0;
        while($i <= $n)
        {
            $sum = ($a + $b) % 1000000007;
            $a = $b;
            $b = $sum;
            $i++;
        }
        return $sum;
    }
}

GO解法

func fib(N int) int {
    a := 0;
    b := 1;
    if N == 0 {
        return 0;
    }
    if N == 1 {
        return 1;
    }
    sum := 0;
    for i := 2; i <= N; i++ {
        sum = (a + b) % 1000000007;
        a = b;
        b = sum;
    }
    return sum;
}

最后