每日算法:最长公共前缀(LCP)
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入: ["flower","flow","flight"]
输出: "fl"示例 2:
输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。解法一:逐个比较
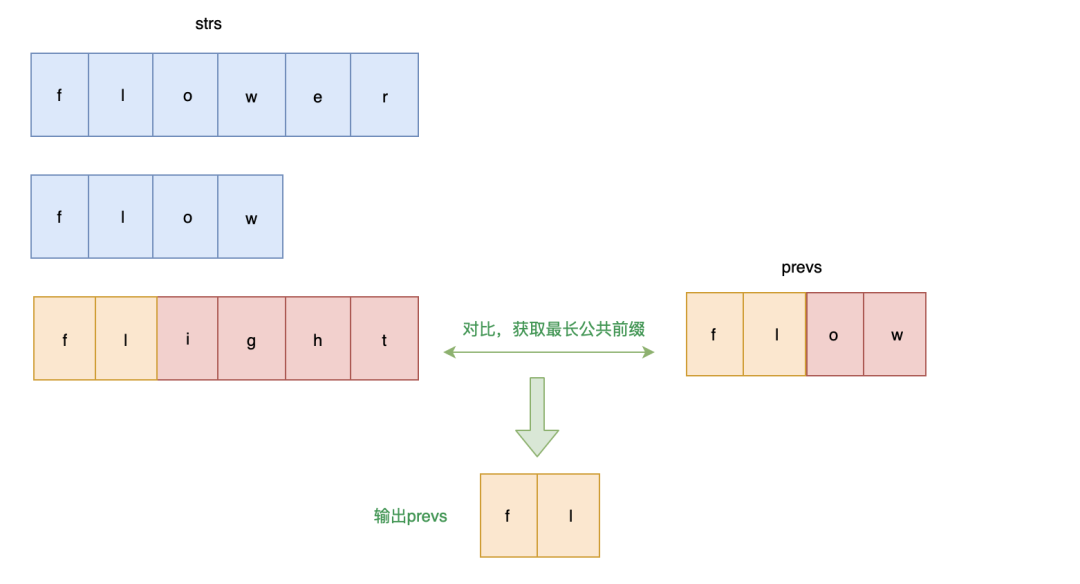
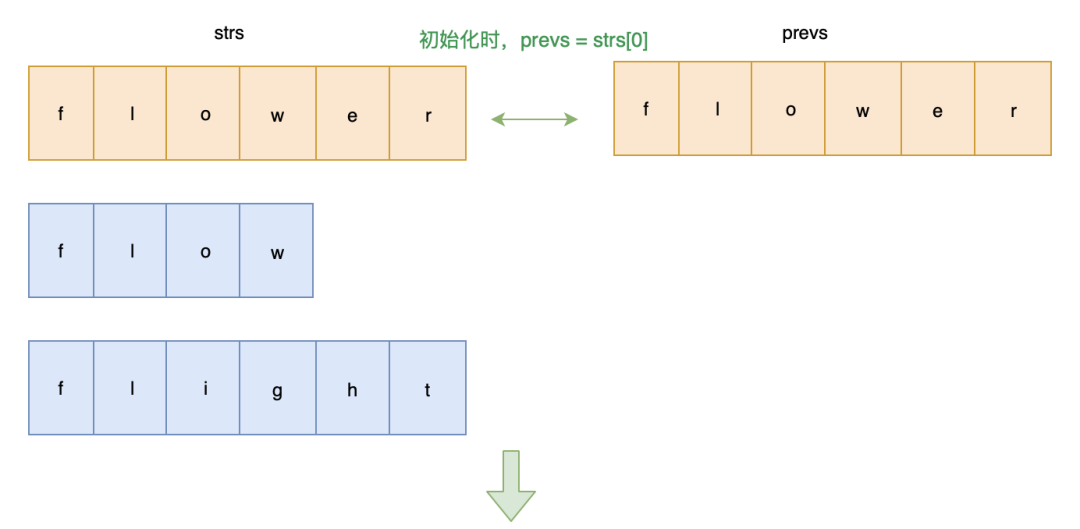
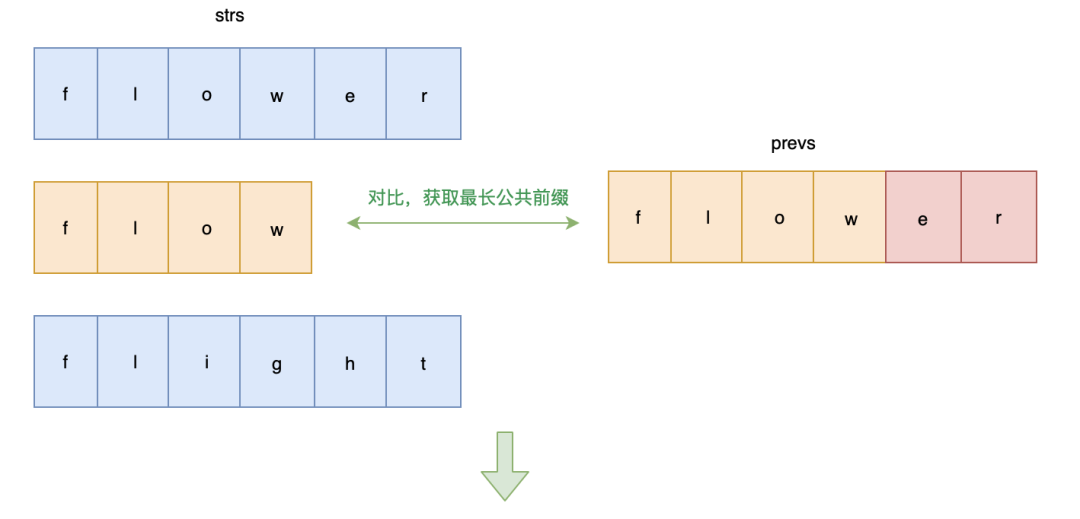
解题思路: 从前往后依次比较字符串,获取公共前缀
画图帮助理解一下:
代码实现:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
let prevs = strs[0]
for(let i = 1; i < strs.length; i++) {
let j = 0
for(; j < prevs.length && j < strs[i].length; j++) {
if(prevs.charAt(j) !== strs[i].charAt(j)) break
}
prevs = prevs.substring(0, j)
if(prevs === "") return ""
}
return prevs
};时间复杂度:O(s),s 是所有字符串中字符数量的总和
空间复杂度:O(1)
解法二:仅需最大、最小字符串的最长公共前缀
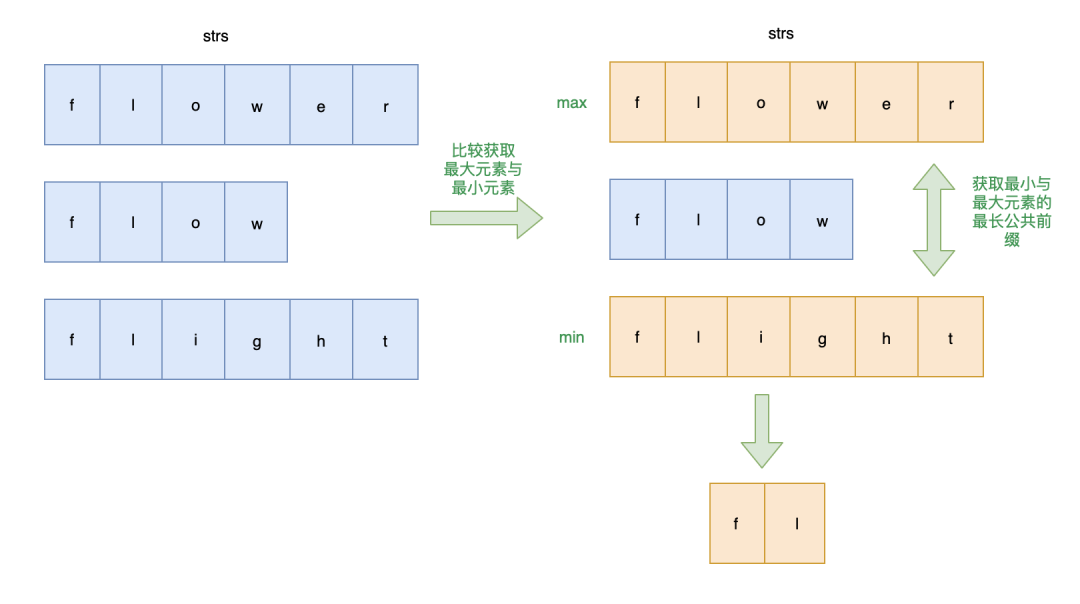
解题思路: 获取数组中的最大值及最小值字符串,最小字符串与最大字符串的最长公共前缀也为其他字符串的公共前缀,即为字符串数组的最长公共前缀
例如 abc 、 abcd 、ab 、ac ,最小 ab 与最大 ac 的最长公共前缀一定也是 abc 、 abcd 的公共前缀
画图帮助理解一下:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
if(strs.length === 1) return strs[0]
let min = 0, max = 0
for(let i = 1; i < strs.length; i++) {
if(strs[min] > strs[i]) min = i
if(strs[max] < strs[i]) max = i
}
for(let j = 0; j < strs[min].length; j++) {
if(strs[min].charAt(j) !== strs[max].charAt(j)) {
return strs[min].substring(0, j)
}
}
return strs[min]
};时间复杂度:O(n+m),n是数组的长度, m 是字符串数组中最短字符的长度
空间复杂度:O(1)
解法三:分治策略 归并思想
分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。
这道题就是一个典型的分治策略问题:
- 问题:求多个字符串的最长公共前缀
- 分解成多个相似的子问题:求两个字符串的最长公共前缀
- 子问题可以简单求解:两个字符串的最长公共前缀求解很简单
- 原问题的解为子问题解的合并:多个字符串的最长公共前缀为两两字符串的最长公共前缀的最长公共前缀,我们可以归并比较两最长公共前缀字符串的最长公共前缀,知道最后归并比较成一个,则为字符串数组的最长公共前缀:
LCP(S1, S2, ..., Sn) = LCP(LCP(S1, Sk), LCP(Sk+1, Sn))
画图帮助理解一下:
以 abc 、 abcd 、ab 、ac 为例:

var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
return lCPrefixRec(strs)
};
// 若分裂后的两个数组长度不为 1,则继续分裂
// 直到分裂后的数组长度都为 1,
// 然后比较获取最长公共前缀
function lCPrefixRec(arr) {
let length = arr.length
if(length === 1) {
return arr[0]
}
let mid = Math.floor(length / 2),
left = arr.slice(0, mid),
right = arr.slice(mid, length)
return lCPrefixTwo(lCPrefixRec(left), lCPrefixRec(right))
}
// 求 str1 与 str2 的最长公共前缀
function lCPrefixTwo(str1, str2) {
let j = 0
for(; j < str1.length && j < str2.length; j++) {
if(str1.charAt(j) !== str2.charAt(j)) {
break
}
}
return str1.substring(0, j)
}时间复杂度:O(s),s 是所有字符串中字符数量的总和
空间复杂度:O(m*logn),n是数组的长度,m为字符串数组中最长字符的长度
解法四:Trie 树(字典树)
Trie 树,也称为字典树或前缀树,顾名思义,它是用来处理字符串匹配问题的数据结构,以及用来解决集合中查找固定前缀字符串的数据结构。
解题思路: 构建一个 Trie 树,字符串数组的最长公共序列就为从根节点开始遍历树,直到:
- 遍历节点存在超过一个子节点的节点
- 或遍历节点为一个字符串的结束字符
为止,走过的字符为字符串数组的最长公共前缀
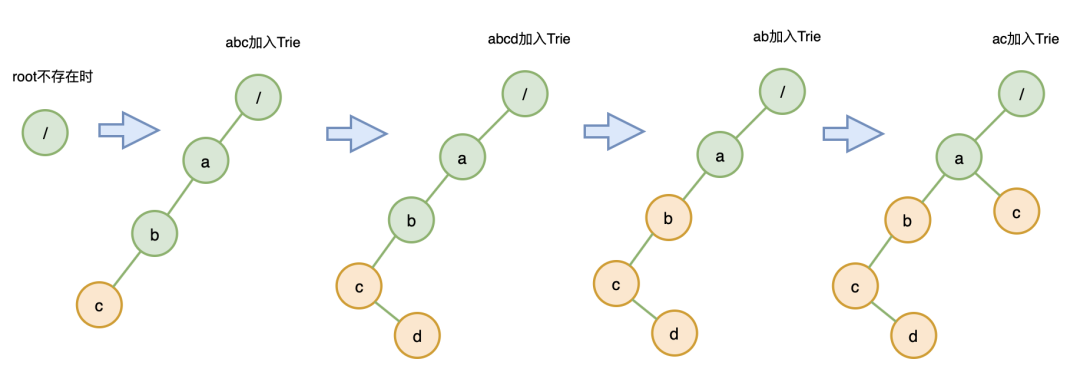
画图帮助理解一下:
构建一个 Trie 树,以 abc 、 abcd 、ab 、ac 为例:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
// 初始化 Trie 树
let trie = new Trie()
// 构建 Trie 树
for(let i = 0; i < strs.length; i++) {
if(!trie.insert(strs[i])) return ""
}
// 返回最长公共前缀
return trie.searchLongestPrefix()
};
// Trie 树
var Trie = function() {
this.root = new TrieNode()
};
var TrieNode = function() {
// next 放入当前节点的子节点
this.next = {};
// 当前是否是结束节点
this.isEnd = false;
};
Trie.prototype.insert = function(word) {
if (!word) return false
let node = this.root
for (let i = 0; i < word.length; i++) {
if (!node.next[word[i]]) {
node.next[word[i]] = new TrieNode()
}
node = node.next[word[i]]
}
node.isEnd = true
return true
};
Trie.prototype.searchLongestPrefix = function() {
let node = this.root
let prevs = ''
while(node.next) {
let keys = Object.keys(node.next)
if(keys.length !== 1) break
if(node.next[keys[0]].isEnd) {
prevs += keys[0]
break
}
prevs += keys[0]
node = node.next[keys[0]]
}
return prevs
}时间复杂度:O(s+m),s 是所有字符串中字符数量的总和,m为字符串数组中最长字符的长度,构建 Trie 树需要 O(s) ,最长公共前缀查询操作的复杂度为 O(m)
空间复杂度:O(s),用于构建 Trie 树