前端也要懂图形学：使用 TypeScript 实现光线追踪 - 哈喽比特

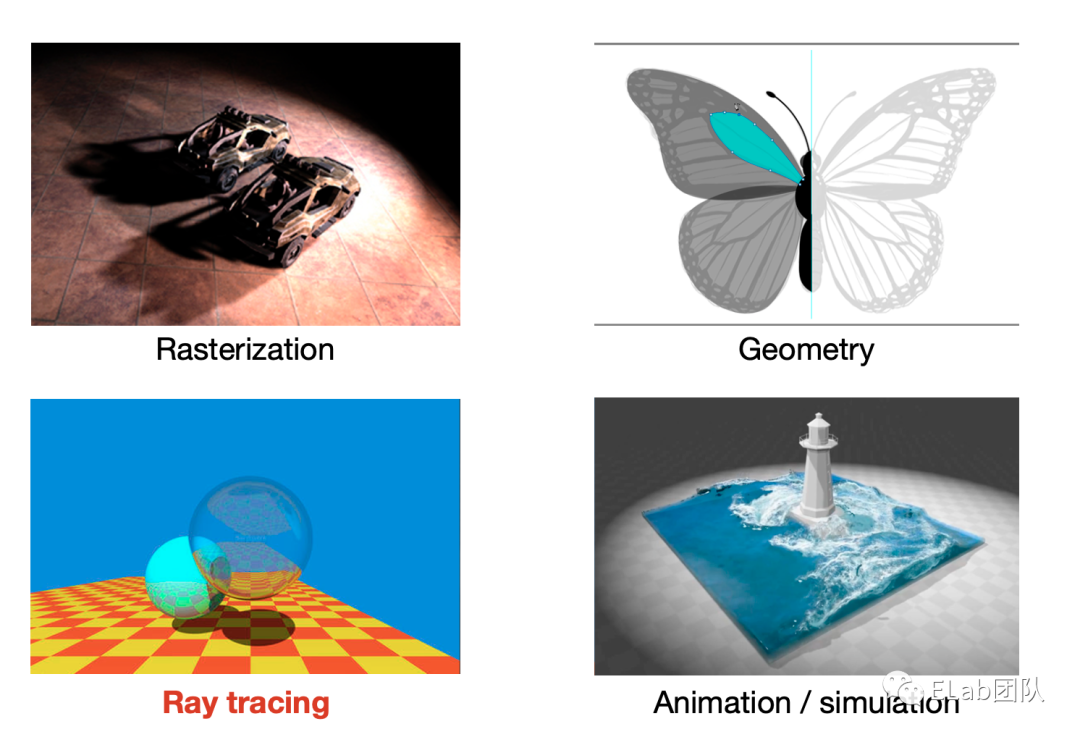
计算机图形学是什么

Rasterization （光栅化）

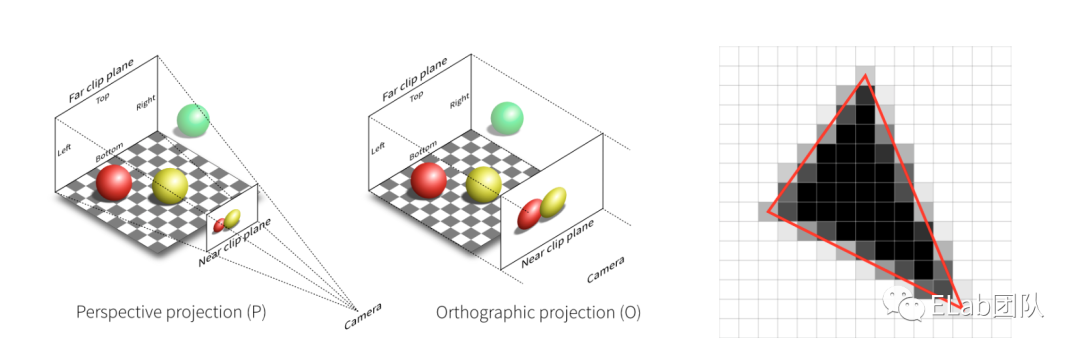
计算机图形学对于我们前端来说可能就是 WebGL，其实 WebGL 所代表的光栅化图形学只是计算机图形学中的一部分。从下图我们可以看到光栅化主要做的工作就将三维空间的球体显示到了一个平面上面，因为我们本次分享都是的工作都是在 CPU 上完成，所以这里就不介绍 GPU 的渲染管线的内容。

将三维空间中的几何形体显示在屏幕上
游戏的首选（实时渲染）

Geometry （几何学）

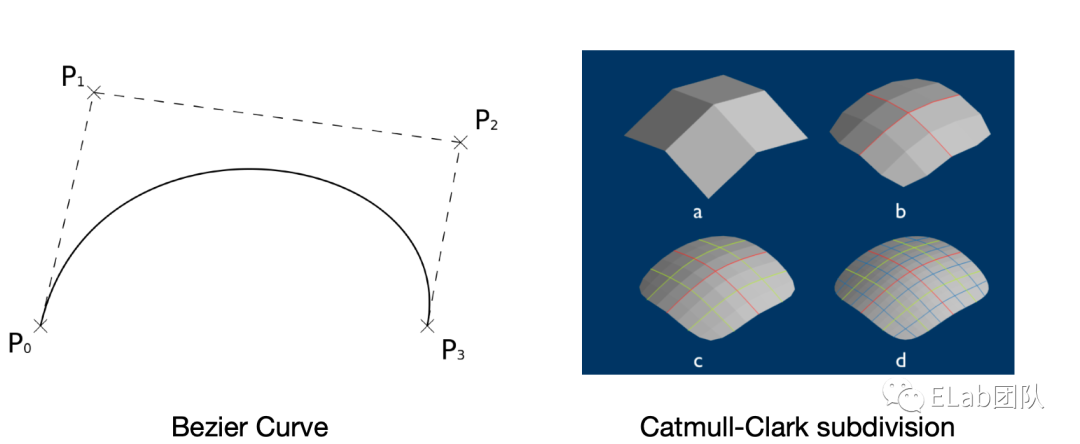
第二点几何学，也就是怎么在计算机中展现几何物体。左边这幅图对于前端来说比较熟悉，贝塞尔曲线，我们可以通过四个特征点确定一条光滑的曲线，所以这一部分干的就是通过一些简单的参数展现出复杂的图形。

Ray tracing （光线追踪）

接下来就的就是我们今天的主题，光线追踪。首先明确一个点，就是光线追踪和光栅化其实是两个平行的关系，他们都是通过输入三维世界中的物体然后通过一系列的计算，最终得到图像。只是光栅化是通过一些方法来达到现实世界中的效果。而光线追踪是模拟真实的物理现象，真实感比较强。右图是光线追踪的结果，可以看到已经和现实没什么区别了。

Animation / simulation （动画/模拟）

最后一点就是动画与模拟，前端对于这个来说比较熟悉，关键帧动画就是 css 中的 keyfarme，当然现在可以通过 lottie 比较方便的实现关键帧动画，然后想说的一点就是质量弹簧系统，就是有些时候我们做的动画并不那么生动，而了解 react-spring 这个库的同学应该知道，他们的演示 demo 是多么的丝滑和舒适，然后我们用代码去描绘动画也不用，使用关键帧和一些缓动函数，我们只需要输入弹性系数，就能得到比较好的效果。

关键帧动画（keyframes, AE, lottie）
质量弹簧系统（react-spring）

然后我们就可以将计算机图形学归纳为下面的的这四幅图，左边的两个做的都是将三维世界中的物体生成一张图片。几何做的是通过一些简单的参数展现出复杂的图形，比如这只蝴蝶。而动画和模拟，就是把场景中的物体动起来。

Why 光线追踪

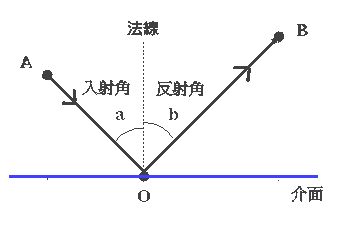
光栅化不能很好的处理全局光照

刚才我们提到了光线追踪和光栅化是一个平行的关系，使用了不同的方法达到相同的目的，为什么要重复发明方法？

光栅化的一个主要问题就是不能很好的处理全局光照，这里提到了一个新的概念全局光照，其实就是真实的光线，因为光线会进行反射和折射，而光栅化只能处理直接光线和弹射一次的光线。从下图可以看到在直接光照下的 p 点附近是黑的。而通过我们经验知道真实世界中不是这样的，可以看到具体的细节的。而再下一张图光线弹射了16次，可以看见 p 点附近亮了起来，是比较符合真实环境的。

光栅化很快但是质量低

当然光栅化对比光线追踪来说优点和缺点都很突出，它很快但是质量真实感比较差，主要用作实时渲染，比如游戏，而光线追踪就和下面这幅图一样，效果很好，但是速度特别慢，主要用在离线渲染，比如动画电影。

光线追踪特别真实，但是比较慢

光线追踪：离线
光栅化：实时
大约需要 10k 的 CPU 时间去渲染一帧

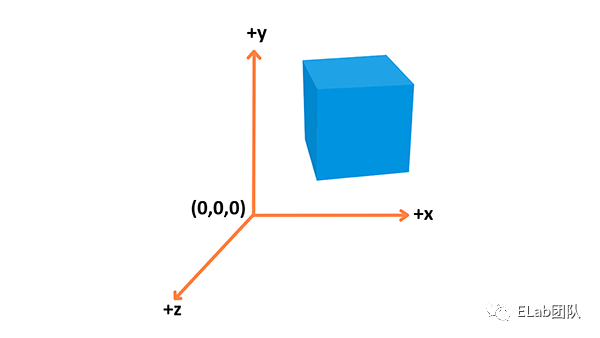
坐标空间

对光线追踪有了一个大致的了解之后，我们来看具体的实现，我们都知道程序是

算法 + 数据结构

我们先来创建我们的特殊的数据结构也就是向量来描述: 坐标，法线和颜色

位置: 在 3D 空间用来确定位置 (x, y, z)
法线: 描述顶点朝向（比如一个平面，在背对法线方向就看不到该平面）
颜色: rgb 值

下面的代码就是我们实现的三维向量的类。主要就实现了向量的四则运算和点乘。因为我们会在整个过程中实例化很多的这个类，所以实际的算法是放在类的静态方法中应该能节省一点内存空间。(因为 TS 没有运算符重载的计划，所以就写成类中的方法)

export default class Vec3 {

  /**

   * 三维向量类 Vec3 ，用它可以在三维空间中表述一个点的

   * 坐标/一个方向

   * 或者表述一个颜色 ( rgb 值 )

   * @param e0

   * @param e1

   * @param e2

   */

  constructor(public e0 = 0, public e1 = 0, public e2 = 0) {}

  // ---------- 静态方法 开始 -----------

        // 加法

  static add(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.add(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.add(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 + v2.e0, v1.e1 + v2.e1, v1.e2 + v2.e2)

  }

        // 减法

  static sub(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.sub(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.sub(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 - v2.e0, v1.e1 - v2.e1, v1.e2 - v2.e2)

  }

        // 乘法

  static mul(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.mul(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.mul(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 * v2.e0, v1.e1 * v2.e1, v1.e2 * v2.e2)

  }

        // 除法

  static div(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.div(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.div(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 / v2.e0, v1.e1 / v2.e1, v1.e2 / v2.e2)

  }

        // 点乘

  static dot(v1: Vec3, v2: Vec3) {

    return v1.e0 * v2.e0 + v1.e1 * v2.e1 + v1.e2 * v2.e2

  }

  // ---------- 静态方法 结束 -----------



  // ----------会挂载到实例上面的方法 开始-----------

  add(v: Vec3 | number) {

    return Vec3.add(this, v)

  }



  sub(v: Vec3 | number) {

    return Vec3.sub(this, v)

  }



  mul(v: Vec3 | number) {

    return Vec3.mul(this, v)

  }



  div(v: Vec3 | number) {

    return Vec3.div(this, v)

  }

  // ----------会挂载到实例上面的方法 结束-----------



  // 单位向量(向量方向)

  unitVec() {

    return this.div(this.length())

  }



  // 向量长度

  squaredLength() {

    return this.e0 ** 2 + this.e1 ** 2 + this.e2 ** 2

  }



  length() {

    return this.squaredLength() ** (1 / 2)

  }

}

光线

关于光线的三个观点

光以直线传播 (虽然这是错的，波粒二象性)
如果光线交叉，它们不会相互“碰撞” (尽管这仍然是错误的)
光线从光源照射到眼睛 (但是逆转之后的结果是正确的, 光路可逆转)

光线类

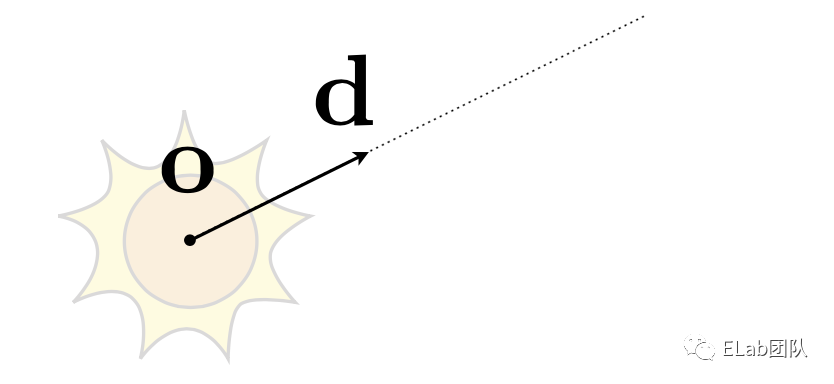
从上图可以看到我们描述一个光线只需要一个原点，以及光线的方向。然后光线是有速度的，它对时间有积累，这样我们就可以将光线抽象成下面的这个方程式，我们可以确定某一条光线在任意时刻他所处的位置。

o: 原点（Vec3）
d: 光线的方向（向量）
t: 光线传播的时间
r(t): 光线在某个时间的位置

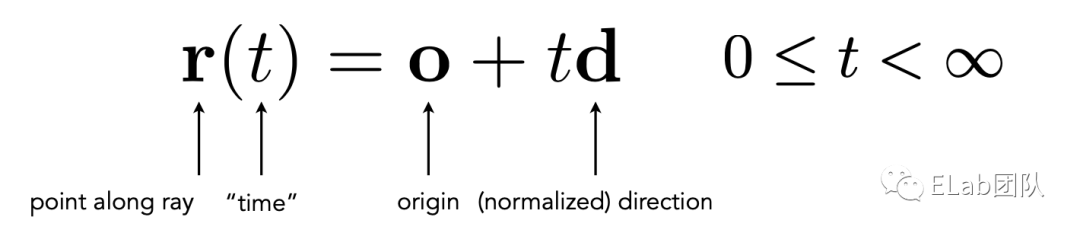
下面的代码就是实现了上面的方程，类的构造函数传入了原点和方向这两个三维向量，然后 getPoint 方法实现了上面方程的算法。

export default class Ray {

  /**

   * 表示光线

   * @param origin 表示光线起始位置的坐标

   * @param direction 方向

   */

  constructor(public origin: Vec3, public direction: Vec3) {}



  /**

   * 计算在时间参数 t 的时候光线的位置

   * @param t 时间参数

   */

  getPoint(t: number) {

    // 相当于：光线原始坐标加上这段时间里面光走的路程

    return this.origin.add(this.direction.mul(t))

  }

}

球

只有光线没有物体我们也没法在场景中看到东西，这里我们选择了在现实世界中不可能出现的东西完美的球体。但是在代码中很好描述。

怎样确定一个球

中心点
半径

export default class Sphere {

  /**

   * 球 (必要信息，球心和半径)

   * @param center 球心坐标

   * @param radius 半径

   */

  constructor(public center: Vec3, public radius: number) {}

}

球和光线怎样产生联系 (碰撞)

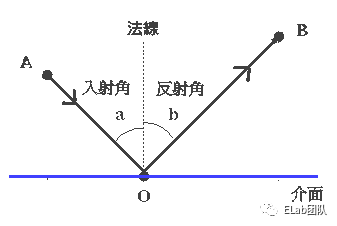
我们都知道现实中的大多数物体是不会发光的比如月球，它是反射太阳的光线才让我们能够看见。而反射光线也就意味着我们会有一条入射光线，打到物体上面的某一点，然后再反射出一条出射光线。

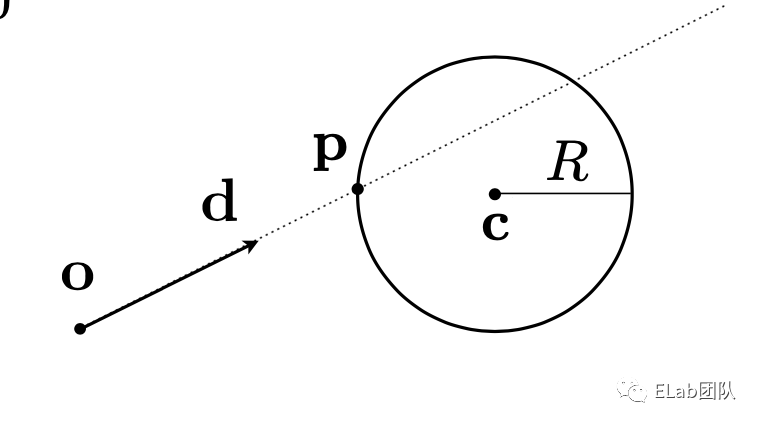
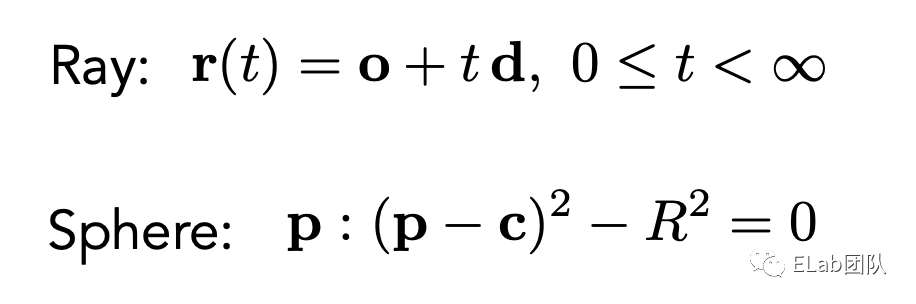
通过我们之前的工作，光线和球体被我们抽象成了两个公式，现在我们只需要将两个方程组联立起来就能得出解了。我们将 r(t) 也就是光在某一点的位置，替换成球公式中的 p 点。可以看到这里构成了一个一元二次方程组，通过求根公式他的解为：

在我们实际写算法之前，我们需要先解决一个问题，怎么将碰撞记录下来，这里我们构建了一个类，里面有三个参数，碰撞时间和位置比较好理解，这个法线我们来讲一下，就是在理想的平面上面入射角和出射角相同，然后他们之间用法线进行分割，所以我们需要记录下法线才让在后面计算出出射光线。

export default class HitRecord {

  /**

   * 碰撞记录

   * @param t 时间参数t

   * @param p 发生碰撞的坐标 p

   * @param normal 发生碰撞时的法线方向 normal

   */

  constructor(

    public t: number = 0,

    public p: Vec3 = new Vec3(0, 0, 0),

    public normal: Vec3 = new Vec3(0, 0, 0)

  ) {}

}

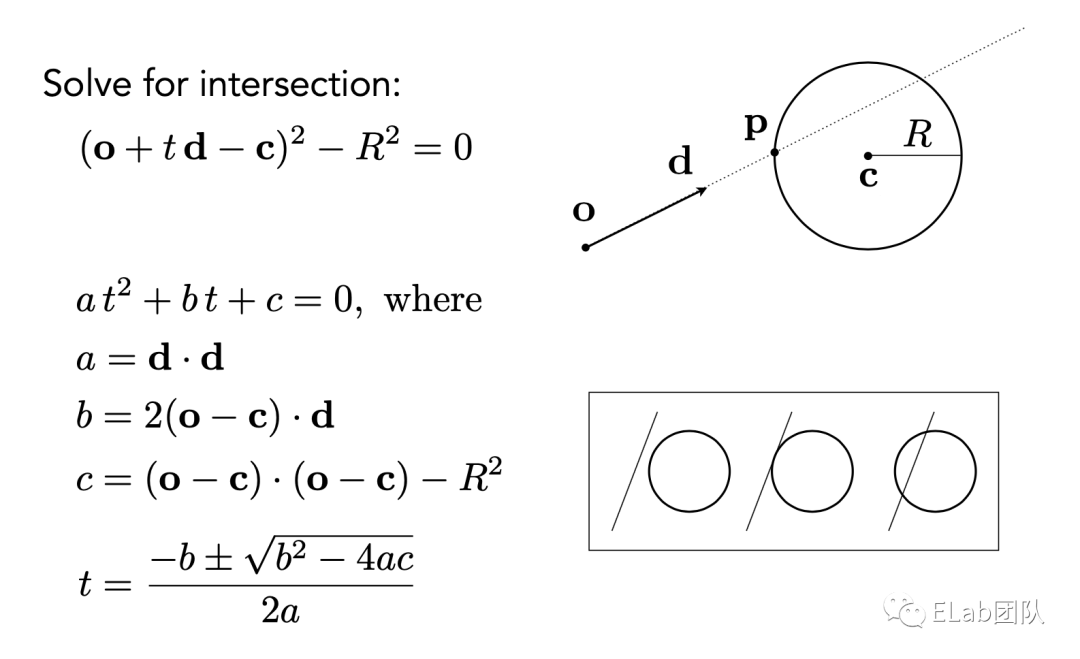
下面就是碰撞实现的具体算法，主要是实现了一个求根公式，求出了碰撞时间 t，然后再依次求出碰撞位置，以及法线，然后再通过后面会实现的光线类中一个方法求出反射光线。

export default class Sphere implements HitableInterface {

        // ...



  hit(ray: Ray, t_min: number, t_max: number): [HitRecord, Ray] | undefined {

    let hit = new HitRecord()



    // 球心和光线原点的连线

    const oc = Vec3.sub(ray.origin, this.center)

    const a = Vec3.dot(ray.direction, ray.direction)

    const b = Vec3.dot(oc, ray.direction) * 2

    const c = Vec3.dot(oc, oc) - this.radius ** 2



    const discriminate = b ** 2 - 4 * a * c



    if (discriminate > 0) {

      let t

      t = (-b - Math.sqrt(discriminate)) / (2 * a)

      if (t > t_min && t < t_max) {

        hit.t = t

        hit.p = ray.getPoint(t)

        // 法线方向

        hit.normal = hit.p.sub(this.center).div(this.radius)



        return [hit, ray.reflect(hit)]

      }

      t = (-b + Math.sqrt(discriminate)) / (2 * a)

      if (t > t_min && t < t_max) {

        hit.t = t

        hit.p = ray.getPoint(t)

        hit.normal = hit.p.sub(this.center).div(this.radius)



        return [hit, ray.reflect(hit)]

      }

    }

  }

}

相机

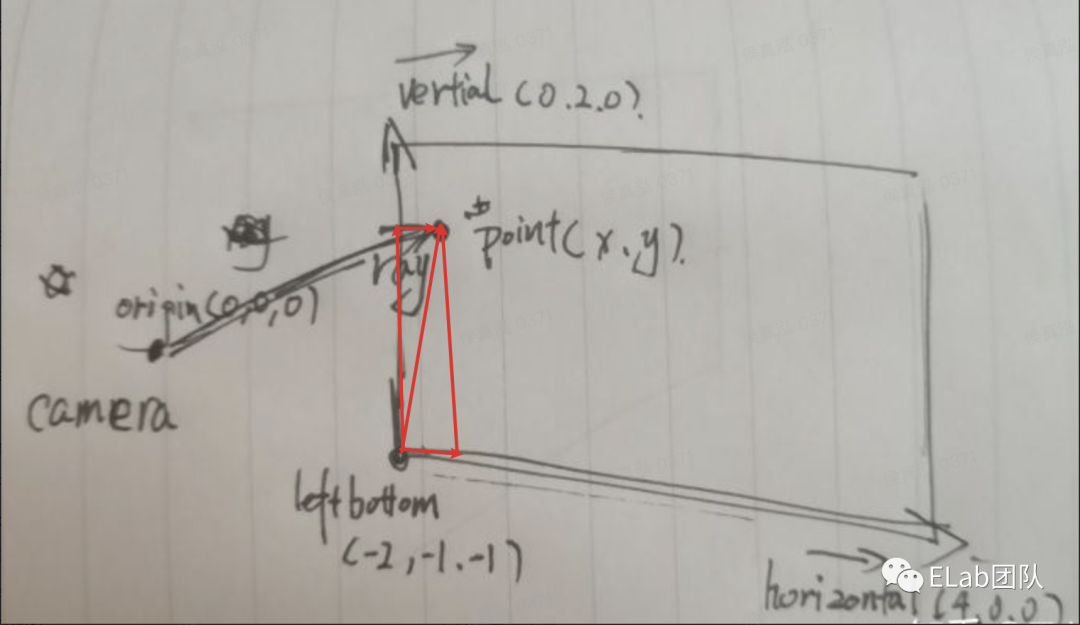
我们现在已经有了空间，光线，球，我们还需要一个相机来观察我们创建的物体。我们之前假设的光线是可逆的，现在把相机假设成一个原点，然后和画布上面的一个像素构成一个连线。这样我们就构成光线的原点和方向。其中原点是我们自己设置的，而得到光线的方向就要复杂一些，我们知道两个坐标相减就得到方向向量，但是这里只有相机的三维坐标我们是知道的，但是画布上面的像素点是一个二维的坐标，我们需要和画布的一些参数通过一些运算得到三维坐标，我们只需要从画布的左下角加上这个像素点在画布水平和垂直的分量，然后我们就得到了像素在三维空间中的位置，然后再减去相机的位置就是光的方向了。

建立一个 Camera 类，假设光线从相机出发。（其中，origin/leftbottom 是坐标，horizontal/vertical 是向量）

export default class Camera {

  /**

   * 

   * @param origin 坐标：相机的位置

   * @param leftBottom 坐标：画面坐下脚的位置

   * @param horizontal 向量：水平向量

   * @param vertical 向量：垂直向量

   */

  constructor(

    public origin: Vec3,

    public leftBottom: Vec3,

    public horizontal: Vec3,

    public vertical: Vec3

  ) {}



  /**

   * 得到光线信息

   * @param x x 坐标

   * @param y y 坐标

   */

  getRay(x: number, y: number): Ray {

    return new Ray(

      this.origin,

      this.leftBottom

        .add(this.horizontal.mul(x))

        .add(this.vertical.mul(y))

        .sub(this.origin)

    )

  }

}

核心算法

现在我们有了全部的铺垫，我们只需要让我们的光跑起来，通过一系列的碰撞最后到达光源，然后得出最终的颜色值。这样我们就得到画布上面一个像素的颜色了，这就是最基础的路径追踪的过程。因为碰撞是一个重复的过程，所以我们实现函数的主体就是一个递归函数。

路径追踪

只有一条光路，不会在场景中分出多个路径。

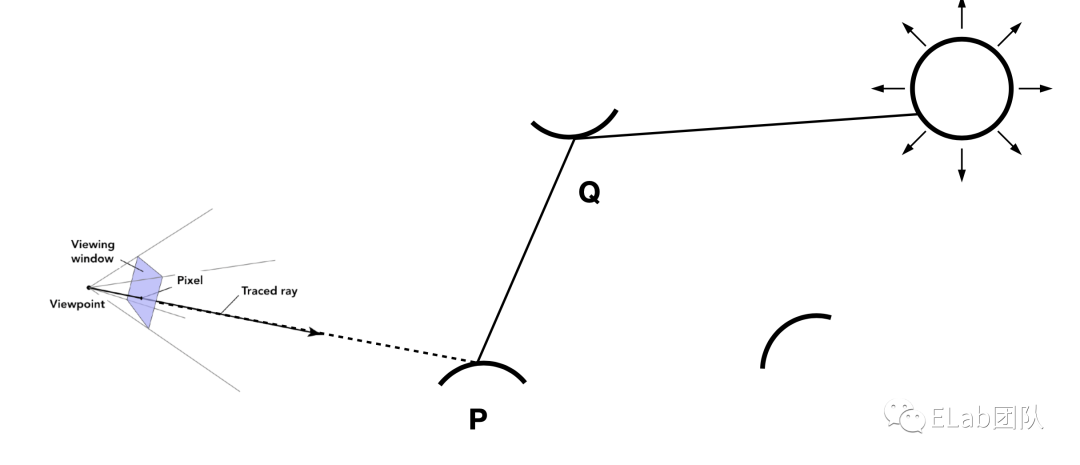
递归函数第一件事情，就是退出条件，不是的话会无限的执行下去。我们这里很粗暴认为如果光线碰撞50次了都没有到达光源的话，我们就认为他的颜色是黑色，现实世界中也是类似的，因为光在弹跳的过程中会损失能量，在50次之后几乎就不剩下多少能量了。

现在我们来看主体逻辑，首先我们会遍历场景中的所有物体，计算出光线和最近的物体相交的点的记录，如果发生碰撞我们将其出射光线作为下一次递归的参数传进去，并在这里简单的认为，这些神奇的物体会对每个波长的光吸收一半的能量。（我们知道物体呈现不同颜色是因为物体对不同波长的光反应不一样）。如果这个光线足够的幸运，没有碰到任何一个物体，我们认为它就到达了我们的光源，我们这里的光源也特别的理想是一个关于坐标轴渐变的颜色。

/**

 * 

 * @param sence 场景中的物体

 * @param r 光线

 * @param step 光线弹射的步数

 */

function trace(sence: HitList, r: Ray, step = 0): Vec3 {

  // 只计算 50 步

  if (step > 50) return new Vec3(0, 0, 0)



  // 遍历场景中的物体，计算出光线和最近的物体相交的点的记录

  // 并返回反射光线

  const hit = sence.hit(r, 0.0000001, Infinity)

        // 返回的结果

  let res: Vec3



  if (hit) {

    // -----命中物体-----

    // 递归

    res = trace(sence, hit[1], ++step).mul(0.5)

  } else {

    // -----命中背景(光源)-----

    // unitDirection 单位向量

    const unitDirection = r.direction.unitVec(),

      // 计算出一个关于 y 坐标的相关数

      t = (unitDirection.e1 + 1.0) * 0.5



    // 计算出一个渐变的颜色值

    res = Vec3.add(new Vec3(1, 1, 1).mul(1 - t), new Vec3(0.3, 0.5, 1).mul(t))

  }

  return res

}

从头开始

我们搞定了基础知识，接下来我们从零开始创建一个简单的路径追踪的场景。(这里选择 snowpack 而不是 vite 唯一的原因是它提供了一个纯的 typescript 模板)

Snowpack

npx create-snowpack-app rey --template @snowpack/app-template-blank-typescript --use-yarn

创建一个 canvas 场景

<div id="app">

      <div class="processbar">

        <div class="processline" id="processline"></div>

      </div>

      <canvas id="cv"></canvas>

</div>

html, body {

    width: 100%;

    height: 100%;

    margin: 0;

    padding: 0;

}



* {

    box-sizing: border-box;

}



#app {

    width: 100%;

    height: 100%;

    position: relative;

    background-color: aquamarine;

}



#app canvas {

    width: 800px;

    height: 400px;

    position: absolute;

    left: 50%;

    top: 50%;

    transform: translate(-50%, -50%);

    box-shadow: 0 4px 12px rgba(0, 0, 0, 0.3)

}





.processbar {

    width: 100%;

    height: 2px;

    position: absolute;

    top: 0;

    background: #fff;

}



.processline {

    width: 0%;

    height: 100%;

    background-color: #90aeff

}

渲染的时候，我们希望尽可能利用电脑的资源，所以可能开多个线程以加速。其中 initTasks 的最后一个参数就是 worker 的数量，有了 worker 就没有阻塞 ui 线程的问题了。

const height = 400

const width = 800



const canvas = document.getElementsByTagName('canvas')[0]

canvas.height = height

canvas.width = width



const ctx = canvas.getContext('2d')

const image = ctx?.createImageData(width, height) as ImageData

const bar = document.getElementById('processline') as HTMLElement

const amount = navigator.hardwareConcurrency - 1



// ...



// 在开发过程中如果不看见就不执行

requestAnimationFrame(() => {

  initTasks(ctx, width, height, amount)

})

在 initTask 中，首先需要获取 canvas 像素总数 n，和每个 task 需要处理的像素数量 len 。然后两层循环每个像素点，外层为纵坐标 y，内层为横坐标 x 。每次循环将新生成 px 实例 push 到 task 里，每当 task 内部的像素数量等于 len 时候或者处理到最后一个像素的时候，执行这个task（ performTask ）。

function initTasks(

  ctx: CanvasRenderingContext2D | null,

  width: number,

  height: number,

  amount: number

) {

  // 获取 canvas 像素总数 n

  const n = width * height

  // 每个 task 需要处理的像素数量 len

  const len = Math.ceil(n / amount)



  // 包装一下，像素点集和宽高

  let task = new RenderTask([], width, height)



  for (let y = 0; y < height; y++) {

    for (let x = 0; x < width; x++) {

      // 然后两层循环每个像素点，外层为纵坐标 y，内层为横坐标 x 。

      // 每次循环将新生成 px 实例 push 到 task 里

      task.pixels.push(new Px(x, y))



      // 每当task 内部的像素数量等于 len 时候或者处理到最后一个像素的时候，

      // 执行这个task（performTask）

      if (task.pixels.length >= len || y * width + x === n - 1) {

        performTask(task, n)

        task = new RenderTask([], width, height)

      }

    }

  }

}

RenderTask 实例记录了图片大小（ width，height ），所有的像素 pixels。

export default class RenderTask {

  constructor(public pixels: Px[], public width: number, public height: number) {

  }

}

其中 Px 实例纪录了一个点的坐标信息和 rgba 值。

export default class Px {

  r: number

  g: number

  b: number

  a: number



  constructor(public x: number, public y: number) {

    this.r = this.g = this.b = this.a = 0

  }

}

在 performTask 这个函数中，我们需要新建一个 Web Worker 执行我们的函数，并将 task 发送到 work 中执行。其中 taskMsg 这个对象是我们用来接收 worker 传回来的结果用的，主要是两个方法，一个是获取结果渲染图片，一个是待所有结果完成后关闭 worker

let complete = 0

function performTask(task: RenderTask, mount: number) {

  const worker = new Worker('./_dist_/task.worker.js', {

    type: 'module',

  })



  worker.postMessage({

    method: 'render',

    args: [task],

  })



  const taskMsg: { [key: string]: Function } = {

    partComplete(worker: Worker, task: RenderTask) {

      task.pixels.forEach((v) => {

        const position = (v.x + v.y * task.width) * 4

        image.data[position] = v.r

        image.data[position + 1] = v.g

        image.data[position + 2] = v.b

        image.data[position + 3] = v.a

      })



      complete += task.pixels.length

      bar.style.width = (complete / mount) * 100 + '%'



      ctx?.putImageData(image, 0, 0)

    },



    allComplete(worker: Worker, task: RenderTask | null) {

      if (task) {

        task.pixels.forEach((v) => {

          const position = (v.x + v.y * task.width) * 4

          image.data[position] = v.r

          image.data[position + 1] = v.g

          image.data[position + 2] = v.b

          image.data[position + 3] = v.a

        })



        complete += task.pixels.length

        bar.style.width =

          (complete / mount > 1 ? 1 : complete / mount) * 100 + '%'



        ctx?.putImageData(image, 0, 0)

      }



      worker.terminate()

    },

  }



  worker.onmessage = function (res: { data: { method: string; args: any[] } }) {

    const { method, args } = res.data

    if (taskMsg[method]) {

      taskMsg[method](worker, ...args)

    } else {

      alert(`app : can't find method (${method})`)

    }

  }

}

接着 task.worker.ts 中我们需要接收到这个消息，并进行计算。

const appMsg: { [key: string]: Function } = {

  render,

}



onmessage = function (e) {

  const { method, args = [] } = e.data



  if (appMsg[method]) {

    appMsg[method](...args)

  } else {

    console.log(`taskWorker: can't find method (${method})`)

  }

}

其中 render 这个函数中将每个像素拆分分别计算，最后将所有计算结果发送回去。

function render(task: RenderTask) {

  const { pixels, width, height } = task



  pixels.forEach((v, i) => {

    RenderPixel(v, width, height)

  })

  ;(<any>postMessage)({

    method: 'allComplete',

    args: [task],

  })

}

renderPixel 这个函数就是下面研究的重点，现在我们用一个简单的函数占个位置先。

export default function RenderPixel(v: Px, width: number, height: number) {

    v.r = v.g = v.b = v.a = 255

}

现在我们已经看到效果了，但是现在一次传递的数据量太大，如果我们场景特别复杂的话，需要很长的时间才能得到结果。所以我们不能一次将结果传回去，而是将结果分批传回去。于是 render 函数应该长这样。

function render(task: RenderTask) {

  const { pixels, width, height } = task

  // -----------

  const len = 400



  let res = new RenderTask([], width, height)



  pixels.forEach((v, i) => {

    RenderPixel(v, width, height)

    res.pixels.push(v)



    // 只算 400 个像素就传回去了

    if (res.pixels.length >= len) {

      ;(<any>postMessage)({

        method: 'partComplete',

        args: [res],

      })



      res = new RenderTask([], width, height)

    }

  })

  ;(<any>postMessage)({

    method: 'allComplete',

    args: [res],

  })

  // -----------

}

在实际渲染过程中，一部分区域的像素计算量比较小，部分比较大。经常会造成 worker 间的工作时间差距比较大。所以我们需要给 worker 随机分配像素。于是将 initTask 修改如下：

function initTasks(

  ctx: CanvasRenderingContext2D | null,

  width: number,

  height: number,

  amount: number,

) {

  const n = width * height

  const len = Math.ceil(n / amount)



  // 用了一个二维数组来存 pixel

  const pixels: Px[][] = []

  // 构建二维数组

  for (let y = 0; y < height; y++) {

    pixels.push([])

    for (let x = 0; x < width; x++) {

      pixels[y].push(new Px(x, y))

    }

  }



  let task = new RenderTask([], width, height)

  while (pixels.length) {

    // 随机取一个 y

    const y = Math.floor(Math.random() * (pixels.length - 0.0001))

    // 选取一行

    const pxs = pixels[y]

    // 随机取一个 x, 且不会取到最后一个

    const x = Math.floor(Math.random() * (pxs.length - 0.0001))

    // 选取一个像素点

    const px = pxs.splice(x, 1)[0]



    task.pixels.push(px)

    // 删除一行

    if (pxs.length == 0) pixels.splice(y, 1)



    if (task.pixels.length >= len || pixels.length == 0) {

      performTask(task, n)

      task = new RenderTask([], width, height)

    }

  }

}

终于终于，我们把框架搭建好了。。。之后的东西，基本上都是之前讲原理的时候讲过

将坐标转换为颜色

之前我们已经有了一个用来占位置的 renderPixel 函数

export default function RenderPixel(v: Px, width: number, height: number) {

  v.r = v.g = v.b = v.a = 255

}

可以看出我们的主要任务就是根据像素坐标位置计算当前坐标的颜色值，所以单独抽象一个 color 函数进行计算颜色，顺便为了方便将坐标范围转换至 [0,1] 。（这里之所以将 y 转换为 1-y ，是应为从 canvas 直接得到的坐标 y 轴的正方向是向下的，而我们更为熟悉的是 y 轴正方向向上的坐标系）

function color( _x: number,  _y: number) {

  const [x, y] = [ _x, 1 -  _y];

  return [x, y, 0.2];

}



export default function RenderPixel(v: Px, width: number, height: number) {

  [v.r, v.g, v.b, v.a] = [...color(v.x / width, v.y / height), 1].map((v) =>

    Math.floor(v * 255),

  );

}

建立坐标系 Vec3

之前我们在讲原理的时候已经讲过了

export default class Vec3 {

  /**

   * 三维向量类 Vec3 ，用它可以在三维空间中表述一个点的

   * 坐标/一个方向

   * 或者表述一个颜色 ( rgb 值 )

   * @param e0

   * @param e1

   * @param e2

   */

  constructor(public e0 = 0, public e1 = 0, public e2 = 0) {}

  // ---------- 静态方法 开始 -----------

        // 加法

  static add(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.add(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.add(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 + v2.e0, v1.e1 + v2.e1, v1.e2 + v2.e2)

  }

        // 减法

  static sub(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.sub(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.sub(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 - v2.e0, v1.e1 - v2.e1, v1.e2 - v2.e2)

  }

        // 乘法

  static mul(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.mul(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.mul(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 * v2.e0, v1.e1 * v2.e1, v1.e2 * v2.e2)

  }

        // 除法

  static div(v1: number | Vec3, v2: number | Vec3): Vec3 {

    return typeof v1 === 'number'

      ? Vec3.div(new Vec3(v1, v1, v1), v2)

      : typeof v2 === 'number'

      ? Vec3.div(v1, new Vec3(v2, v2, v2))

      : new Vec3(v1.e0 / v2.e0, v1.e1 / v2.e1, v1.e2 / v2.e2)

  }

        // 点乘

  static dot(v1: Vec3, v2: Vec3) {

    return v1.e0 * v2.e0 + v1.e1 * v2.e1 + v1.e2 * v2.e2

  }

  // ---------- 静态方法 结束 -----------



  // ----------会挂载到实例上面的方法 开始-----------

  add(v: Vec3 | number) {

    return Vec3.add(this, v)

  }



  sub(v: Vec3 | number) {

    return Vec3.sub(this, v)

  }



  mul(v: Vec3 | number) {

    return Vec3.mul(this, v)

  }



  div(v: Vec3 | number) {

    return Vec3.div(this, v)

  }

   // ----------会挂载到实例上面的方法 结束-----------



  // 单位向量(向量方向)

  unitVec() {

    return this.div(this.length())

  }



  // 向量长度

  squaredLength() {

    return this.e0 ** 2 + this.e1 ** 2 + this.e2 ** 2

  }



  length() {

    return this.squaredLength() ** (1 / 2)

  }

}

建立光线

export default class Ray {

  /**

   * 表示光线

   * @param origin 表示光线起始位置的坐标

   * @param direction 方向

   */

  constructor(public origin: Vec3, public direction: Vec3) {}



  /**

   * 计算在时间参数 t 的时候光线的位置

   * @param t 时间参数

   */

  getPoint(t: number) {

    // 相当于光线原始坐标加上这段时间里面光走的路程

    return this.origin.add(this.direction.mul(t))

  }

}

建立相机

export default class Camera {

  /**

   *

   * @param origin 坐标：相机的位置

   * @param leftBottom 坐标：画面坐下脚的位置

   * @param horizontal 向量：水平向量

   * @param vertical 向量：垂直向量

   */

  constructor(

    public origin: Vec3,

    public leftBottom: Vec3,

    public horizontal: Vec3,

    public vertical: Vec3,

  ) {}



  /**

   * 得到光线信息

   * @param x x 坐标

   * @param y y 坐标

   */

  getRay(x: number, y: number): Ray {

    return new Ray(

      this.origin,

      this.leftBottom

        .add(this.horizontal.mul(x))

        .add(this.vertical.mul(y))

        .sub(this.origin),

    )

  }

}

生成背景

修改 color 函数，已经有了相机和光，现在可以根据光的方向生成一个背景。

const camera = new Camera(

  new Vec3(0, 0, 1), //origin

  new Vec3(-2, -1, -1), //leftBottom

  new Vec3(4, 0, 0), //horizontal

  new Vec3(0, 2, 0), //vertical

)



function color(_x: number, _y: number) {

  const [x, y] = [_x, 1 - _y]



  // 从相机发出一道光线

  const r = camera.getRay(x, y)



  // 设置背景色

  // unitDirection 单位向量

  const unitDirection = r.direction.unitVec(),

    // 计算出一个关于 y 坐标的相关数

    t = (unitDirection.e1 + 1.0) * 0.5



  // 计算出一个渐变的颜色值

  // 两个加起来

  const res = Vec3.add(

    // (1, 1, 1) * (1 - t)

    new Vec3(1, 1, 1).mul(1 - t),

    // (0.3, 0.5, 1) * t

    new Vec3(0.3, 0.5, 1).mul(t),

  )



  return [res.e0, res.e1, res.e2]

}

添加一个球

在添加一个球之前，我们需要先写一个 interface，因为在我们这个世界中假设，球和一组球（场景中的所有物体）都是能够被光线击中的。

所以我们需要抽象出一个 HitableInterface 接口，包含一个hit 方法，根据光线 r ，和时间参数范围 tmin/t_max ，返回一个记录 HitRecord。

一个 HitRecord 中包含着，时间参数t，和发生碰撞的坐标 p ，和发生碰撞时的法线方向 normal 。

// hitRecord.ts



export default class HitRecord {

  /**

   * 碰撞记录

   * @param t 时间参数t

   * @param p 发生碰撞的坐标 p

   * @param normal 发生碰撞时的法线方向 normal

   */

  constructor(

    public t: number = 0,

    public p: Vec3 = new Vec3(0, 0, 0),

    public normal: Vec3 = new Vec3(0, 0, 0)

  ) {}

}



// hitable.interface.ts

export default interface HitableInterface {

  /**

   * 和光线发生作用

   * @param ray 光线

   * @param t_min 时间范围

   * @param t_max 时间范围

   */

  hit: (

    ray: Ray,

    t_min: number,

    t_max: number,

  ) => HitRecord | undefined

}



type HitResult = ReturnType<HitableInterface['hit']>



export type { HitResult }

然后我们再来实现一个球，其中算法已经在原理部分讲了

export default class Sphere implements HitableInterface {

  /**

   * 球 (必要信息，球心和半径)

   * @param center 球心坐标

   * @param radius 半径

   */

  constructor(public center: Vec3, public radius: number) {}



  hit(ray: Ray, t_min: number, t_max: number) {

    let hit = new HitRecord()



    const oc = Vec3.sub(ray.origin, this.center)

    const a = Vec3.dot(ray.direction, ray.direction)

    const b = Vec3.dot(oc, ray.direction) * 2

    const c = Vec3.dot(oc, oc) - this.radius ** 2



    const discriminate = b ** 2 - 4 * a * c



    if (discriminate > 0) {

      let temp

      temp = (-b - Math.sqrt(discriminate)) / (2 * a)

      if (temp > t_min && temp < t_max) {

        hit.t = temp

        hit.p = ray.getPoint(temp)

        hit.normal = hit.p.sub(this.center).div(this.radius)



        return hit

      }

      temp = (-b + Math.sqrt(discriminate)) / (2 * a)

      if (temp > t_min && temp < t_max) {

        hit.t = temp

        hit.p = ray.getPoint(temp)

        hit.normal = hit.p.sub(this.center).div(this.radius)



        return hit

      }

    }

  }

}

将球添加到场景中

新建一个球 new Sphere(new Vec3(0, 0, -1), 0.5) 。修改 color 函数，如果光线与球碰撞返回（0，1，0），否则返回背景色。

// ...

const ball = new Sphere(new Vec3(0, 0, -1), 0.5)



function color(_x: number, _y: number) {

  const [x, y] = [ _x, 1 -  _y];



   // 从相机发出一道光线

  const r = camera.getRay(x, y);

  const hit = ball.hit(r, 0, Infinity)

  let res: Vec3

  if (hit) {

    res = new Vec3(0, 1, 0)

  } else {

    // 设置背景色

    const unitDirection = r.direction.unitVec(),

      t = (unitDirection.e1 + 1.0) * 0.5



    res = Vec3.add(new Vec3(1, 1, 1).mul(1 - t), new Vec3(0.3, 0.5, 1).mul(t))

  }

  return [res.e0, res.e1, res.e2]

}

创建一个场景的组

还记得之前的我们创建的 HitableInterface 接口吗？当时说因为球和一组球（场景中的所有物体）都是能够被光线击中的，所以才创建了这个接口，我们已经实现了球，然后我们就需要实现这一个组了。也就是 HitList 类，同样要实现 HitableInterface 接口。它实例化的时候需要传入这个场景中能被击中的物体 HitableInterface[] ,它的 hit 方法，就是分别调用内部所有 HitableInterface 的 hit 方法，选最小的结果传出。

export default class HitList implements HitableInterface {

  // 这个组中的物体

  list: HitableInterface[]



  constructor(...arg: HitableInterface[]) {

    this.list = arg

  }



         // 分别调用内部所有 HitableInterface 的 hit 方法 ，选最小的结果传出

  hit(ray: Ray, t_min: number, t_max: number) {

    let closest_t = t_max,

      hit: HitResult = undefined



    this.list.forEach((v) => {

      let _hit = v.hit(ray, t_min, t_max)

      if (_hit && _hit.t < closest_t) {

        hit = _hit

        closest_t = _hit.t

      }

    })

    return hit

  }

}

添加多个球


// renderPixel.ts

// ....

// const ball = new Sphere(new Vec3(0, 0, -1), 0.5)

const ball1 = new Sphere(new Vec3(0, 0, -1), 0.5)

const ball2 = new Sphere(new Vec3(1, 0, -1), 0.5)

const ball3 = new Sphere(new Vec3(-1, 0, -1), 0.5)

const earth = new Sphere(new Vec3(0, -100.5, -1), 100)



const world = new HitList(ball1, ball2, ball3, earth)



// ...





function color(_x: number, _y: number) {

        // ...



  // const hit = ball.hit(r, 0, Infinity)

  const hit = world.hit(r, 0, Infinity)

        // ...

}

光的反射

因为我们在 hitrecord 中已经保存了这次碰撞的法线方向，反射光的方向根据入射光和法线的方向就可以算出。先求出入射光线延法线方向的分向量，然后入射光线减去两倍这个分向量的值就是反射光方向

export default class Ray {

  // ....



  reflect(hit: HitRecord) {

    return new Ray(hit.p, reflect(this.direction.unitVec(), hit.normal))

  }

}



// 计算出反射光线

// 先求出入射光线延法线方向的分向量，然后入射光线减去两倍这个分向量的值就是反射光方向

function reflect(v: Vec3, n: Vec3) {

  return v.sub(n.mul(Vec3.dot(v, n) * 2))

}

这样只要出现碰撞记录（HitRecord）的地方我们都需要进行修改，添加反射光线，这里不把反射光线放到碰撞记录中，可以从上 Ray 中的 reflect 方法的参数中可以发现，反射光线是通过碰撞记录（HitRecord）计算出来的。那我们开始修改吧。

首先是 HitableInterface 接口，因为这里定义了 hit 方法的实现

// hit: (ray: Ray, t_min: number, t_max: number) => HitRecord | undefined

hit: (ray: Ray, t_min: number, t_max: number) => readonly [HitRecord, Ray] | undefined

然后就是两个实现的地方
球(sphere.ts)

// return hit

return [hit, ray.reflect(hit)] as const

场景组(hitList.ts)

// _hit.t

_hit[0].t

光线追踪

终于的终于，现在，我们有了光线在每一点的入射，出射信息，那么只要有一个起点，我就能知道整条光线的路径，然后我们就可以路径追踪了。

先将 color 函数中由根据光获取颜色这一部分抽离出来

function color(_x: number, _y: number) {

    const [x, y] = [_x, 1 - _y]



    const r = camera.getRay(x, y)



    const res = trace(world, r)



    return [res.e0, res.e1, res.e2]

}

在 trace 函数里我们获取了 hit 结果中反射光线，再带入 trace 递归。为了防止无限递归下去，trace 中加入了 step 参数，反射数量超过了50次，就直接返回黑色。

function trace(sence: HitableInterface, r: Ray, step = 0): Vec3 {

  if (step > 50) return new Vec3(0, 0, 0)



  const hit = sence.hit(r, 0.0000001, Infinity)



  let res: Vec3



  if (hit) {

    res = trace(sence, hit[1], ++step).mul(0.5)

  } else {

    // 设置背景色

    const unitDirection = r.direction.unitVec(),

      t = (unitDirection.e1 + 1.0) * 0.5



    res = Vec3.add(new Vec3(1, 1, 1).mul(1 - t), new Vec3(0.3, 0.5, 1).mul(t))

  }

  return res

}

我们就实现了一个简单的路径追踪的东西了，但是就上面这 18 行的代码中也有许多可以优化的地方

遍历场景中的物体的时候是将所有的物体都计算了一遍他们是否相交，如果有一个物体在你的身后是不可能看见的，但是我们都将他们进行了计算，有一种优化方法就是将空间分成多个包围盒，只有光线进入某个包围盒才计算其中的物体。
我们在处理光线反射衰减的时候是对所有波长的光都以同样方式进行处理，也就不会有颜色，贴图之类的东西了。
对循环的结束条件的处理我们也很粗暴，我们假设光线弹射50次就直接认为其是黑色了，其实可以用更随机的方式，但是这个时候就引出另外的问题，因为我们每个像素弹跳的次数不同，就会有很多的噪声，我们需要通过一些方法去除噪声。

虽然有许多的不足，但是上面内容还是将一个光线追踪的框架搭建了起来。

我之前在写的时候就感觉到了这个内容似乎和前端没有什么关系，虽然说使用了前端的一些技术比如 canvas，web worker，但是在其他环境语音下也有其他的方式实现。这和我们平时的前端的 2D 渲染，甚至 WebGL 都相差比较远。但是给我感受就是，无论编写怎么样的程序都是算法加数据结构，优化方法也有不计算看不见的东西，怎么用类的方式来描述现实中的物体之类的。所以给我并不只有光线追踪的方法，还有一些编程的思想。

参考

https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html

https://raytracing.github.io/books/RayTracingInOneWeekend.html

https://zhuanlan.zhihu.com/p/42218384