草系前端手摸手带你实现正则引擎，点燃秋日最热情的烟火

297次阅读  |  发布于3年以前

序章

对读者的话

前一阵，我发了一篇文章前端学编译原理（一）：编译引论，粗略的介绍了一下编译原理这门学科，我也想到一个问题：

“单纯枯燥的讲解编译原理这门课程大家可能并不会很接受这系列文章，并且单纯的讲解编译原理肯定有很多人比我讲的要好要细致。

”

所以我做了这样一个决定：我是一个前端，读我文章的大多数人可能也是前端，所以我不妨接下来将前端的一些应用或者实践和编译原理结合起来。所以这篇文章是本系列的全新实践，如果大家喜欢可以留下你们的点赞 或者关注➕，你们的支持是我更文的最大动力。

本篇文章，我将从自动机出发，扩展到我们常用的正则匹配，最后我也会带着大家亲手实现一个简单的正则匹配。干货满满，也会有一己之言，如果大家有疑问或者指正请留在评论区，我会仔细阅读。

“仓库地址：js-regular，照例放出仓库的地址，请各位大佬忽视我没写gitignore不小心把node_modules上传上来了，失误，纯属失误

”

文章大纲

那么我们咸盐少许（闲言少叙），开始我们的正篇吧～

有限自动机基础

章节引论—有限自动机（FA）

“tip: 如果看不懂特点和形式定义中的话，请大家移步后面我来总结一下部分，帮助大家对有限自动机的定义有一个粗略的理解。

”

首先在开始下面的话题之前，我们有必要去了解一下，什么是有限自动机， 有限自动机也被称为：时序机。

有限自动机有以下特点：

有限自动机的形式定义：

有限状态自动机是一个五元组 M=(Q, Σ, δ, q0, F)，其中：

我来总结一下：

大家不要被上面列出的一大堆定义和特点绕晕，其实总结起来非常简单：

image.png

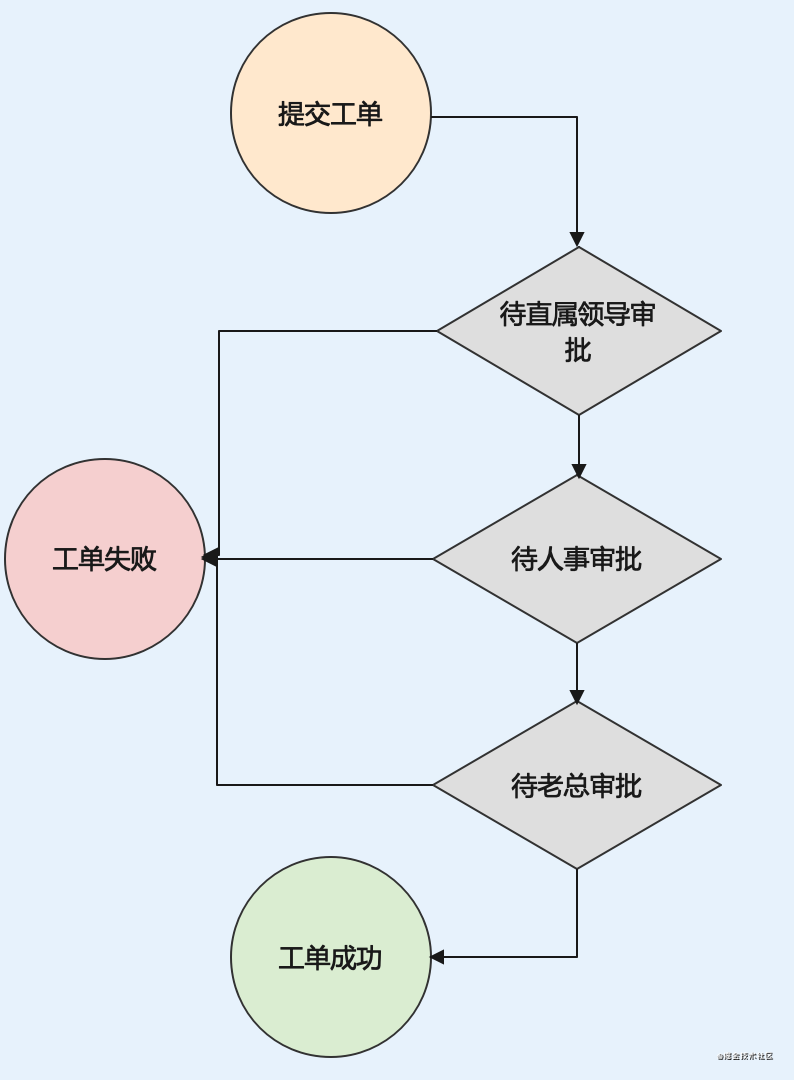
不知道经过我的举例之后，大家有没有对定义有了一定的理解，其实总结起来很简单，其实：

“有限自动机 = 有限的内部状态集合 + 一组控制规则

”

DFA — 确定有限自动机

定义

前文我们已经了解了有限自动机，那么确定有限自动机有哪些特别的点呢，下面我们来看一下确定有限自动机的定义：

我来总结一下：

“我们其实可以和上面的形式定义做一个比较，我们会发现一些很重要的点：

  • 初始状态唯一
  • 状态转换函数是单值函数
  • 终止状态集Z可以为空

”

举个例子

M=({S,U,V,Q}, {a, b}, f, S, {Q}), 其中f定义为：

f(S, a)=U f(S, b)=V

f(U, a)=Q f(U, b)=V

f(V, a)=U f(V, b)=Q

f(Q, a)=Q f(Q, b)=Q

那么我们就可以画出它对应的自动状态机

image.png

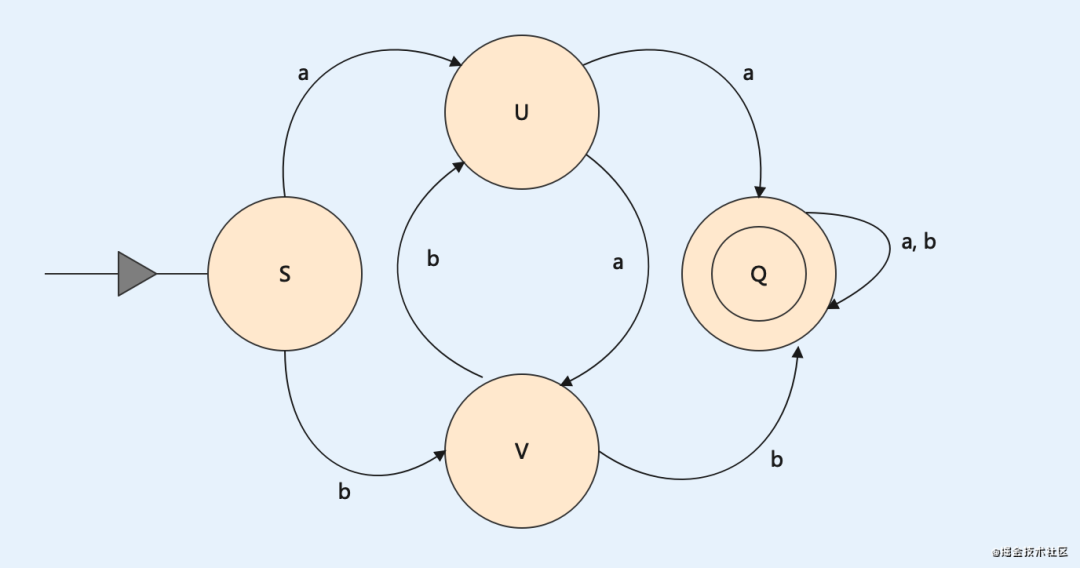
DFA接受的字符串

再次举个例子说明，如果一个自动机是这样的：

image.png

那么：L(M1) = { aba, abaa, abab, abaab,...} 大家有没有发现，正则匹配的雏形已经有了

DFA的确定性

那么我们为什么说 DFA 是确定有限自动机呢，确定这两个字体现在哪里呢？

DFA如何代码实现

比如自动机如图所示：

image.png

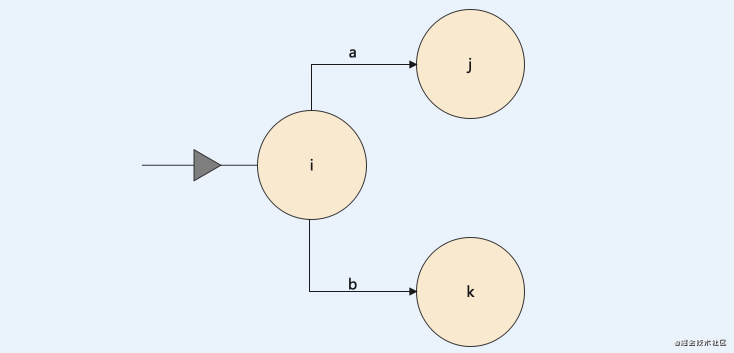
其实我们想要实现简易的 DFA 自动机可以借助 swicth case 实现


// 简单写个switch
switch (currentChar) {
    case 'a':
        goto Lj;
        break;
    case 'b':
        goto Lk;
        break;
    default:
        throw err;
}

NFA — 非确定有限自动机

定义

非确定有限自动机M为一个五元组 M = ( S, ∑, S0, f, Z)

“注意，这里的后继状态不是单一状态，而是状态集S的子集, 即转换函数不是单值.

”

我这里总结一下，大家看区别就是状态转换函数的结果不再是单值了, 起始状态也这是一个集合而不是一个确定的值，以及转换函数的的输入是∑∪{ε}就表示有向弧上面的标记可以是空。

举个例子

NFA M = ({0, 1, 2}, {a, b}, f, {0}, {2})
状态转换函数如下：
f(0,a)={0,1} f(1,a)=∅ f(2,a)={2}
f(0,b)={0} f(1,ε)={2} f(2,b)={2}

那么我们就可以画出它对应的有限自动机

image.png

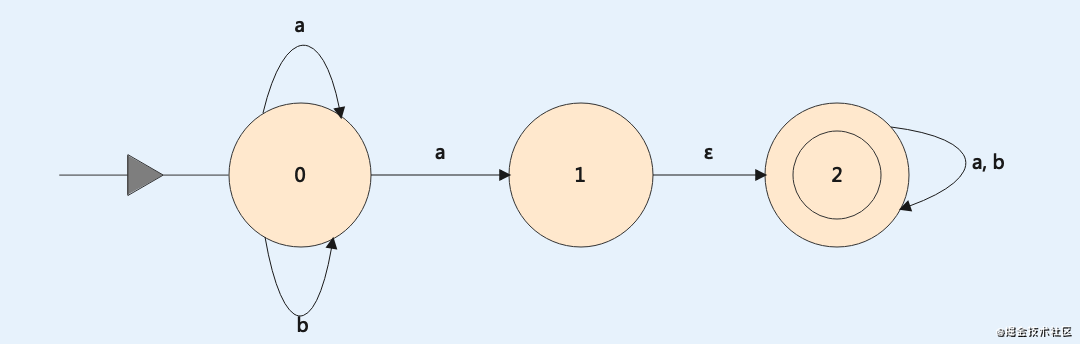
NFA接受的字符串

设M是一个NFA，M=(S, ∑, f, S0, Z)，则定义L(M)为从任意初始 状态到任意终止状态所接受的字符串的集合，我们拿上面的自动机举例。上面自动机接受的字符串集合是：L(M) =ββ是形如...a...的由a, b构成的字符串

比如：aaa, bab, abaa...

DFA 与 NFA 对照

那在本章结束之前，我们回顾一下～

DFA：

NFA：

更多扩展内容

“tip: 此处还会很多值得讲的内容，比如 NFA 到 DFA 的转换, DFA的化简等，但是因为文章内容有限，而且与本文主题关系不大，感兴趣的人可以留言，我们继续开坑。当然我也更加鼓励大家自我学习。

”

正则原理浅析

“本章节部分内容参考：正则表达式引擎执行原理——从未如此清晰！，这篇文章也有很多可以了解的内容大家也可以去围观一下，我从这篇文章学到很多，总结整理的很好。

”

前文我们已经讲解过了 DFA 和 NFA，即确定有限自动机和非确定有限自动机，根据前面的铺垫想必各位大佬已经可以将正则引擎与自动机关联起来了，而正则引擎大体也可以分成这样的两大类，即：DFA 正则引擎和 NFA 正则引擎。

DFA引擎

举个例子

我们直接举一个比较简单的例子：

正则表达式是 a[db]c 待匹配的字符串是 abc

“此处我们使用‘[]’的原因是第三章手摸手，带你实现简易版正则引擎我们将会去实现‘[]’

”

下面我们开始匹配：

image.png

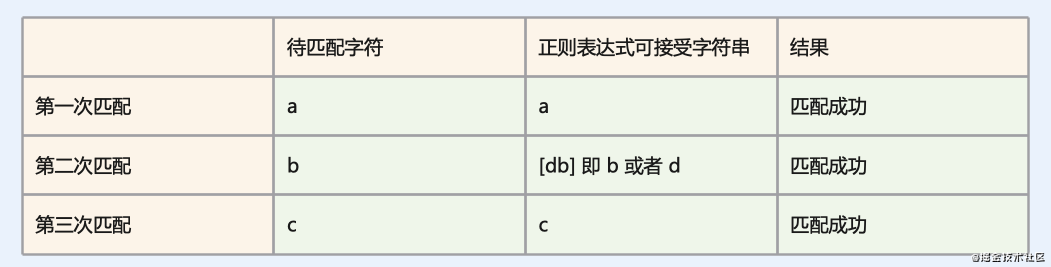
不知道大家有没有理解，我描述一下对比的过程：

  1. 第一次是字符 a 和正则表达式 a 比较
  2. 匹配成功后，是字符 b 同时比较表达式中的 b 和 d
  3. 再次匹配成功，字符 c 和正则表达式 c 比较
  4. 匹配成功

这里面我们值得注意的点是，第二次匹配是 b 同时和 b， d 进行比较，所以可能会消耗更多的内存。

特点

我们从上面的例子可以看出一些DFA正则引擎的特点：

NFA引擎

举个例子

例子还是刚才的例子，方便大家对照：

正则表达式是 a[db]c 待匹配的字符串是 abc

下面我们开始匹配：

image.png

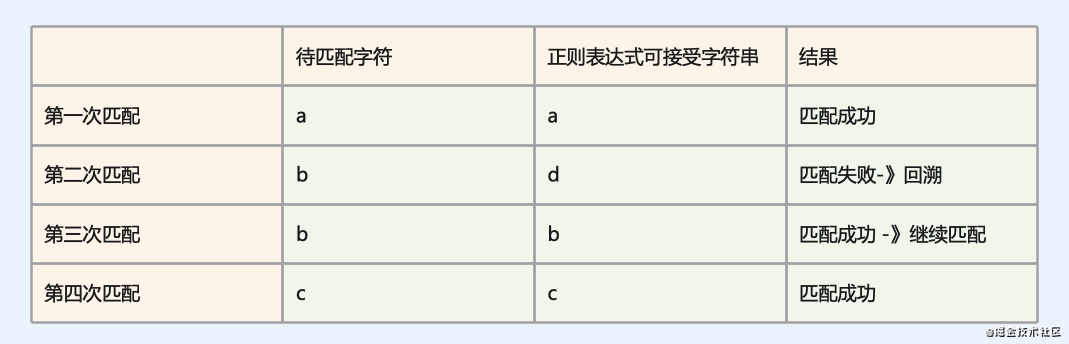
这里和前面的DFA模式做一下对比，我们会发现区别，NFA引擎在匹配之前会记录字符的位置，然后选择其中一个可能状态进行匹配，如果匹配失败，会进行回溯，进入其他分支进行匹配。

特点

我们从上面的例子可以看出一些NFA正则引擎的特点：

对比

image.png

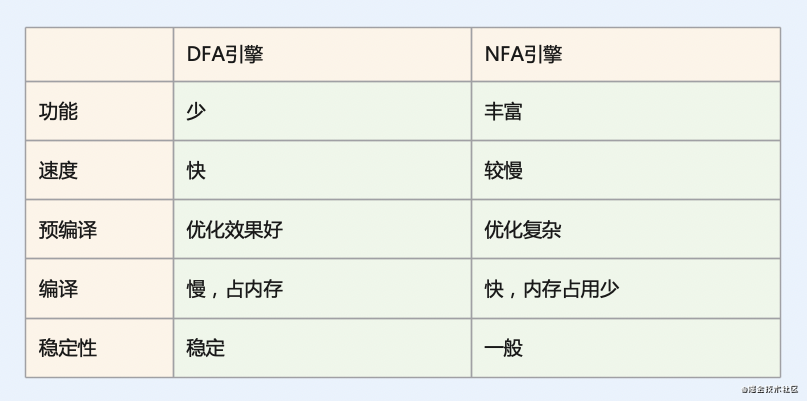
章节小结

本章结束大家已经获得了所有前置知识，下面我们会利用这些知识去亲手实现一个简单的正则，也是本文的重点，下面我们一起进入下一章的内容吧

手摸手，带你实现简易版正则引擎

章节序言

功能介绍：

“入口方法介绍：我们要提供一个方法，testReg，参数有两个，一个是待验证的字符串str，另一个是正则表达式reg，返回一个布尔值，即是否匹配

正则表达式规则介绍：

  • 这个正则表达式要以 ^ 开头，以 $ 结尾
  • [] 表示匹配字符集合中的一个字符，[] 后可以接 * 或者 +
  • * 表示匹配 0 个或者 0 个以上多个
  • + 表示匹配 1 个或者 1 个以上的多个

”

// 正则表达式举例
^[123]*mn[ab]+cd$
^a[ab]+$
...

仓库地址：js-regular

思路解析

我们遇到一个问题，需要先思考，有了思路之后再进行编码，避免重复修改导致代码的混乱以及时间的浪费。

那么，我们首先要思考我们的目标是啥，既然我们本篇文章的主题是自动机，也没必要卖关子， 我们第一步想到的肯定是， 把正则表达式转换成自动机， 之后借助这个正则匹配的自动机去匹配我们的字符串。

那么我们如何把一个正则表达式转换成一个自动机呢？ 我的思路是这样的：

graph TD
正则表达式 --> 具有匹配含义的独立单元序列 
具有匹配含义的独立单元序列 --> 正则匹配自动机

我来简单解读一下，我会把这个问题分成两部分，首先我需要解析字符串，之后转换成具有匹配含义的独立单元序列，即 TOKEN 序列。什么叫做具有匹配含义的独立单元序列呢？

我举个例子：

正则表达式是 ^[123]+[a]*3$， 那么其它可以分成三个独立单元即：

之后我们要把 具有匹配含义的独立单元序列（我真的是起名鬼才）转换成自动机，既然我们都说了我会用对象表示每个独立单元， 那最简单的方法就是在这个对象中加入 next 属性， 当然 next 可能是一个数组， 存储着所有可能的分支。

之后我们再写一个方法， 让自动机跑起来就好了。

ok，说干就干，下面我们将进入代码分步骤展示与解读环节，请大家跟着我一起思考。

入口方法 - testReg

// the entry function
const testReg = (str, reg) => {
    if (!reg.startsWith('^') || !reg.endsWith('$')){
        // it's not a right reg string
        throw Error('format mismatch！');
    }
    const generator = getGeneratorStart(reg);
    return isMatch(str, generator);
    //console.log(matchStructure)
}

入口方法很直白， 大家看我这里接受两个参数， 第一个 str 是待匹配的字符串， 第二个 reg 是正则表达式。

首先我对正则表达式做了验证，如果正则表达式不以 ^ 开头，以 $ 结尾， 表示这个表达式是无效的，是不合法的。之后我们调用了 getGeneratorStart 方法获取了自动机的开始状态， 之后调用 isMatch 方法对字符串进行一个匹配。

获取自动机方法 - getGeneratorStart

// use reg to get generator and return start Pattern Object
const getGeneratorStart = (reg) => {
    const regStr = reg.slice(1, reg.length - 1);
    const patternObjList = getPatternObjList(regStr);
    const generator = getGenerator(patternObjList);
    return generator;
}

又是一个很短很直白的方法， 第一步我们对正则表达式做了一个截取，掐头去尾（去掉开头的 ^ 和结尾的 $ ），留下真正有效的部分。之后我们又调用了两个方法 getPatternObjList 和 getGenerator 。这两个方法和之前我在思路解析中表达的一致:

获取单元序列方法 - getPatternObjList

// change reg String to Pattern Ojects and return list
const getPatternObjList = (regStr) => {
    const len = regStr.length;
    let patternObjlist = [];
    let isInCollection = false;
    let collection = []; // used to store current collection
    for (let i = 0; i < len; i++) {
        const char = regStr[i];
        if (!isInCollection) {
            // 
            if (char != '[') {
                // single char object
                patternObjlist.push({
                    isCollection: false,
                    pattern: [char],
                    next: []
                })
            } else {
                // char === [ we need to change isInCollection to true
                isInCollection = true;
            }
        } else {
            if (char != ']') {
                collection.push(char);
            } else {
                // ] is the sign end of collection
                isInCollection = false;
                // collectionSign maybe * or + 
                let collectionSign = regStr[i + 1];
                let collectionType = 'COMMON';
                if( collectionSign && collectionTypes.includes(collectionSign) ){
                    collectionType = collectionSign
                    i++;
                }
                patternObjlist.push({
                    isCollection: true,
                    pattern: collection,
                    collectionType,
                    next: []
                })
                collection = [];
            }
        }
    }
    return patternObjlist;
}

这个方法比较长，但其实就是字符串的一遍遍历， 其实看上去比较简单， 但是值得注意的是我把具有匹配含义的独立单元序列转换成的数据结构：

{
    isCollection: Boolean,
    pattern: Array,
    collectionType: emun,
    next: Array
}
{
    isCollection: Boolean,
    pattern: Array,
    next: Array
}

其中

我给大家演示一下方法的输入输出：

输入：
^[123]+[a]*3$
输出：
[
  {
    isCollection: true,
    pattern: [ '1', '2', '3' ],
    collectionType: '+',
    next: []
  },
  {
    isCollection: true,
    pattern: [ 'a' ],
    collectionType: '*',
    next: []
  },
  { 
    isCollection: false, 
    pattern: [ '3' ], 
    next: [] 
   }
]

单元序列转换为自动机方法 - getGenerator

// change pattern list to regular generator
const getGenerator = (patternObjList) => {
    patternObjList.push({
        isEnd: true,
    }) // the end signal of generator
    let start = {
        isStart: true,
        next:[]
    }; // generator need a 'start' to start valid
    const len = patternObjList.length;
    start.next = getNext(patternObjList, -1);
    for(let i = 0; i < len; i++ ){
        const curPattern = patternObjList[i];
        curPattern.next = getNext(patternObjList, i)
        if(collectionTypes.includes(curPattern.collectionType)){
            curPattern.next.push(curPattern);
        }
    }
    return start;
}

我们先给 getPatternObjList 方法返回值数组加入起始状态和结束状态。之后我们给起始状态的 next 初始化，之后循环遍历数组，为数组的每一项的 next 初始化，这样就通过 next 中存储的指针将自动机的各个状态串联起来了。

“注意：这里 next 数组的每一项都是 patternObjList 数组中对象的引用。以及最后如果 collectionType 是 * 或者 + 还要把自己追加进去，这类的节点可以自循环

”

之后我们看一下其中的子方法 getNext ，我就不单独开一个章节了，因为这两个方法关联性很强。

// get PatternObj's next
const getNext = (patternObjList, index) => {
    let next = [];
    const len = patternObjList.length;
    for(let i = index + 1; i < len; i++){
        const nextPattern = patternObjList[i]
        next.push(nextPattern)
        if(nextPattern.collectionType != '*'){
            // * need to handle, * is possible no
            break;
        }
    }  
    return next;
}

其实最关键就是处理 * ，因为 * 表示 0 个或者 0 个以上的多个，就要继续往后遍历。

“比如 a[b]*c 这样的正则表达式，a 后面跟的可能是 b 也可能是 b 后面的 c

”

最后我们可以看一下这个自动机的输出

输入：
^[123]+[a]*3$
输出：
// 这里因为可能有循环引用的关系，所以输出会有问题，但是大家也可以通过这个结构一窥究竟
{
  isStart: true,
  next: [
    {
      isCollection: true,
      pattern: [Array],
      collectionType: '+',
      next: [Array]
    }
  ]
}

自动机图例展示

输入：^[123]+[a]*3$ 图例：

image.png

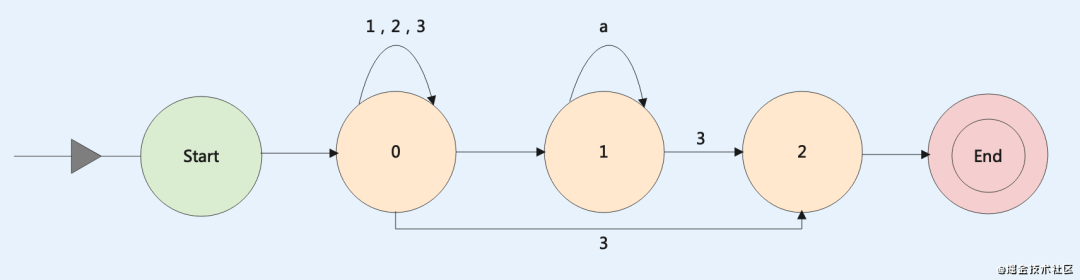
验证匹配方法 - isMatch

// use generator to test string
const isMatch = (str, generator) => {
    if(generator.isStart){
        // the start of recursive
        for(const nextGen of generator.next){
            if(isMatch(str, nextGen)) return true;
        }
        return false;
    } else if(generator.isEnd){
        // if generator is end but str is not end return false
        return str.length ? false : true;
    } else {
        if(!str.length){
            return false;
        }
        if(!generator.pattern.includes(str[0])) {
            return false;
        } else {
            const restStr = str.slice(1);
            for(const nextGen of generator.next){
                if(isMatch(restStr, nextGen)) return true;
            }
            return false;
        }
    }
}

这里其实就是一个递归程序：

输出演示

image.png

结果正确

完整代码

方便大家复制粘贴或者完整回顾，是不是很贴心❤️

const collectionTypes = ['*', '+'];

// change reg String to Pattern Ojects and return list
const getPatternObjList = (regStr) => {
    const len = regStr.length;
    let patternObjlist = [];
    let isInCollection = false;
    let collection = []; // used to store current collection
    for (let i = 0; i < len; i++) {
        const char = regStr[i];
        if (!isInCollection) {
            // 
            if (char != '[') {
                // single char object
                patternObjlist.push({
                    isCollection: false,
                    pattern: [char],
                    next: []
                })
            } else {
                // char === [ we need to change isInCollection to true
                isInCollection = true;
            }
        } else {
            if (char != ']') {
                collection.push(char);
            } else {
                // ] is the sign end of collection
                isInCollection = false;
                // collectionSign maybe * or + 
                let collectionSign = regStr[i + 1];
                let collectionType = 'COMMON';
                if( collectionSign && collectionTypes.includes(collectionSign) ){
                    collectionType = collectionSign
                    i++;
                }
                patternObjlist.push({
                    isCollection: true,
                    pattern: collection,
                    collectionType,
                    next: []
                })
                collection = [];
            }
        }
    }
    return patternObjlist;
}

// get PatternObj's next
const getNext = (patternObjList, index) => {
    let next = [];
    const len = patternObjList.length;
    for(let i = index + 1; i < len; i++){
        const nextPattern = patternObjList[i]
        next.push(nextPattern)
        if(nextPattern.collectionType != '*'){
            // * need to handle, * is possible no
            break;
        }
    }  
    return next;
}

// change pattern list to regular generator
const getGenerator = (patternObjList) => {
    patternObjList.push({
        isEnd: true,
    }) // the end signal of generator
    let start = {
        isStart: true,
        next:[]
    }; // generator need a 'start' to start valid
    const len = patternObjList.length;
    start.next = getNext(patternObjList, -1);
    for(let i = 0; i < len; i++ ){
        const curPattern = patternObjList[i];
        curPattern.next = getNext(patternObjList, i)
        if(collectionTypes.includes(curPattern.collectionType)){
            curPattern.next.push(curPattern);
        }
    }
    return start;
}

// use reg to get generator and return start Pattern Object
const getGeneratorStart = (reg) => {
    const regStr = reg.slice(1, reg.length - 1);
    const patternObjList = getPatternObjList(regStr);
    const generator = getGenerator(patternObjList);
    return generator;
}

// use generator to test string
const isMatch = (str, generator) => {
    if(generator.isStart){
        // the start of recursive
        for(const nextGen of generator.next){
            if(isMatch(str, nextGen)) return true;
        }
        return false;
    } else if(generator.isEnd){
        // if generator is end but str is not end return false
        return str.length ? false : true;
    } else {
        if(!str.length){
            return false;
        }
        if(!generator.pattern.includes(str[0])) {
            return false;
        } else {
            const restStr = str.slice(1);
            for(const nextGen of generator.next){
                if(isMatch(restStr, nextGen)) return true;
            }
            return false;
        }
    }
}

// the entry function
const testReg = (str, reg) => {
    if (!reg.startsWith('^') || !reg.endsWith('$')){
        // it's not a right reg string
        throw Error('format mismatch！');
    }
    const generator = getGeneratorStart(reg);
    return isMatch(str, generator);
    //console.log(matchStructure)
}
console.log(testReg('2131aa3', '^[123]+[a]*3$'));

章节小结

本章我们用前面几章所学的知识实现了一个简易的正则，当热真正的正则引擎要复杂的多的多，也会有预编译等我还没有接触过的流程。但是文章领进门，修行还是在个人的，相信大家与我一同完成这个简易的正则匹配之后也会获得一些解决问题的思路，或者多了一些思考，感谢大家与我一起体验这个过程 ，与你们一起学习成长。

Copyright© 2013-2020

All Rights Reserved 京ICP备2023019179号-8