深度剖析UIScrollView与阻尼动画

309次阅读  |  发布于3年以前

摘要

UIScrollView是iOS开发中不可或缺也是使用最多的基础组件；常用的Feed流、Pager、轮播图等等都与其存在密不可分的联系。日常开发中，我们通常局限于必要的几个调用接口和代理，而不曾探究隐藏在几个简单接口背后的故事，比如：滚动视图如何在有限的区域内展示无限的内容？每一次在滚动区域触控屏幕会产生哪些反应？它在现实世界中又是怎样的物理形态？本文从基本的参数观测开始，以数学、物理学和优化方法中的一些基本方法和概念为工具，探索UIScrollView流畅交互背后隐藏的规律，共同领略苹果工程师的精妙设计。

UIScrollView的局部显示原理

为了印证这部分观点，我们从苹果的官方文档上摘抄了一段描述：

Documents：UIScrollView is the superclass of several UIKit classes, including UITableView and UITextView.

A scroll view is a view with an origin that’s adjustable over the content view. A scroll view tracks the movements of fingers, and adjusts the origin accordingly[1]. The view that shows its content through the scroll view draws that portion of itself according to the new origin, which is pinned to an offset[2] in the content view. By default, it bounces[3] back when scrolling exceeds the bounds of the content.

这段文字的大意有以下几点：

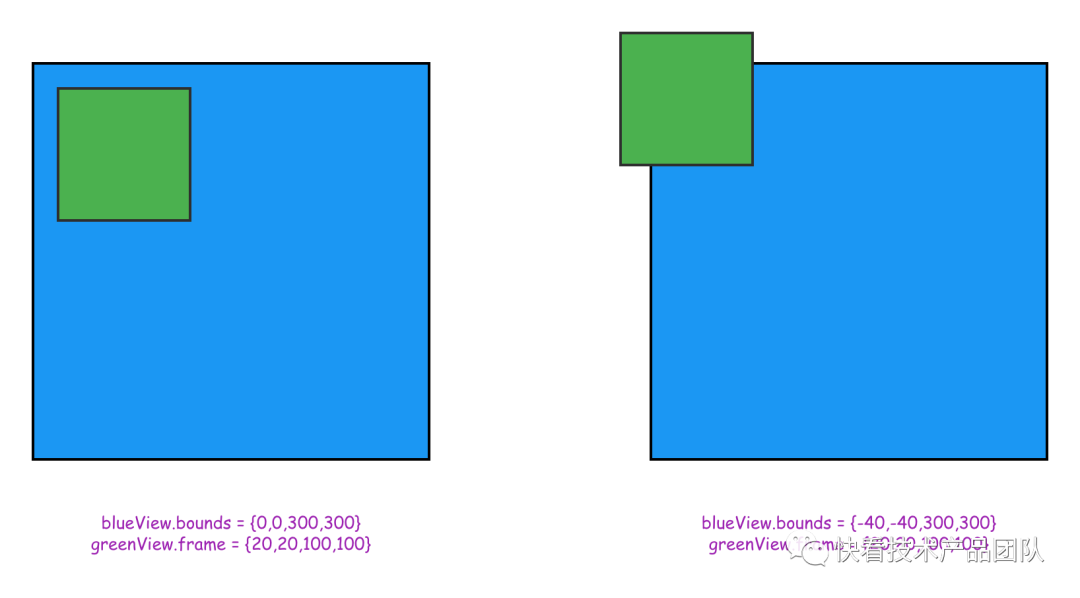
从UIScrollView的父类UIView的角度出发，UIView的属性：bounds.origin(x,y) 标记了一个UIView的所有子元素依赖的参考系原点，被添加在这个UIView上的所有子视图在绘制时均会参考这个原点，这意味着：如果这个原点被标记为{-40, -40.f}，那么这个视图的所有子视图都会基于(-40, -40)这个点绘制。例如，这种情况下，一个frame = {20.f,20.f,100.f,100.f} 的子视图 会从点(-20.f, -20.f) 开始绘制,-20的来源是子视图的原点(20,20)加偏移量(-40,-40)，所以，在此种情况下你只能看到这个子元素右下角大小为20*20的一小部分,其余超出边界的部分无法看到。

图片1.png

在UIScrollView中，为了将这个特性与常规的UIView区分开来，bounds.origin 被独立出来叫做：contentOffset,两者都包含两个数值x、y的二维向量(CGPoint)，只要根据用户手势、动画规律不断变更contentOffset，就能做出滚动的效果。

UIScrollView交互细节

我们汇总了在setContentOffset的之前需要考虑的所有情况：

  1. 当panGesture在容器的规定范围(contentSize)内生效时，UIScrollView通常要移动相同的位置和方向，contentOffset与panGesture位移距离保持1:1数值关系。
  2. 在panGesture结束后，如果Gesture有剩余速度依然生效，需要持续进行减速。
  3. 在panGesture结束后，如果当前的contentOffset超出了contentSize，需要反弹并恢复到边界。
  4. (2)和(3)结合，panGesture结束后，有速度依然生效，在之后的一段时间内减速，减速未结束触及边界，回弹到非拉伸状态。
  5. 根据正交向量互不影响，弹性和减速需要在x、y两个方向上独立生效。
  6. 在超过边界进行panGesture时，panGesture转化为contentOffset距离的有效比例逐渐减小，呈现出一种拉扯到极限的效果。

这些交互特性共同作用成就了UIScrollView的绝佳交互体验。

Decelerate运动探究

1.数值观测

由简入繁，首先从比较容易的Decelerate动画开始，观察这部分动画的运行规律，我们不妨创建一个常规的UIScrollView，在以下代理中打印出统计信息 ：

- (void)scrollViewWillEndDragging:(UIScrollView *)scrollView withVelocity:(CGPoint)velocity targetContentOffset:(inout CGPoint *)targetContentOffset
{
    NSLog(@"DecelerateVelocity:%lf", velocity.y);
    NSLog(@"DecelerateDistance:%lf", targetContentOffset->y - scrollView.contentOffset.y);
}

我们截取了几次panGesture手势结束瞬间捕获到的数据，为了保证不受到bounces和边界的影响，应当尽量保证这些减速过程中不会触及边界，数据如下：

序号 减速初速度 截止到停止的移动距离
1 5.0270956 2506.5
2 1.802126 895.0
3 1.412374 700.5
4 1.687861 838.0

关于这个1000倍：我们从这个代理的注释中可以看出：

Called on finger up if the user dragged. velocity is in points/millisecond. targetContentOffset may be changed to adjust where the scroll view comes to rest

那么这个速度的单位是points/millisecond，而通常的速度应以points/second为单位；因此，我们默认为这个速度乘1000以方便之后的计算，同时我们将1point的宽/高视为单位长度1米，这样速度单位也被我们统一为标准速度单位：m/s。

2.结果分析

根据上面的观察结果，我们试图寻找一种常用的函数，这个函数的特点是：他对时间(t)的导数(v)似乎总他自身(y)的两倍。

显然这个函数和其导数分别是：

这两个函数是指数加速，而由于Decelerate是减速，所以我们需要根据实际情况增加一个负号来保证速度总是随着时间逐渐减小的，所以有：

（细心的同学可以发现除了指数增加了负号外，常数前面也加了一个负号，这是因为我们在上述观测数值的时候velocity直接使用了初速度，而位移却是用了末位移减初位移；而正确的做法是使用速度改变量，也就是,因为末状态是停止状态；因此真正的结论应该是：速度的改变量应当总是位移改变量的-2倍，但此前为了数值观测方便，没有强调正负关系。）

那么根据已知条件：当减速刚开始时，，因此，右侧的常系数可以被固定为；而则是一个跟初始位置相关的常数，此处我们不关心。

那么最终我们得到的速度衰减公式为：

3.相关解释

以下是正常的推导来解释那个突兀的指数函数。

以不同的速度、开始的减速效果满足相同的运动规律，不妨令>，那么是减为0的必经状态，那么根据之前的观察结果：

，两式相减：

当v1与v2无限接近时：

两边同时除以时间间隔dy:

两边积分：

显然;

4.结论

UIScrollView的减速运动就是阻尼系数为2的阻尼运动，这种阻尼运动对应于现实中的低速流体阻力。

5.其他

Bounces运动探索

1.数值观测

我们如法炮制Decelerate观测过程，主要从时间空间两个维度观察Bounces运动规律，那么观测数值包括：

具体的统计方法在此只做简要介绍，读者可自行编写Demo进行实践：

经过这些记录后，我们成功捕获了几组数据：

序号 接触边界时初速度(p/s) Bounces最远距离(p) Bounces持续时间(s)
1 986.497 -32.5 0.6668
2 2404.116 -80.5 0.7509
3 1793.594 -60 0.7337
4 1251.628 -41.5 0.6836

观察到的现象：

那么显然Bounces中存才的两种力：弹力和阻力；弹力用来保证接触到边界发生反弹，阻力用来限制弹力的简谐振动。

2.结果分析

我们列出经过以上两种合力的数学模型：

另外一个我们熟知的结论是：瞬时速度是位移对时间的导数；瞬时加速度是速度对时间的导数，也就是位移间导数。那么上述方程可写成如下形式：

等式两侧同除质量m:

这是个二阶线性齐次微分方程，根据其特征根返程解个数有三种不同形式通解，为了方便讨论特征根，我们对其系数做一些代换，令：

δω注意，由于等式中已经考虑了符号，所以阻尼系数和进度系数在此处均为正数；关于质量, 我们不考虑质量小于等于0的情况；因此，这些参数均为正数，代换后也为正数。

那么这个式子化简为：

δω其特征根方程为：

λδλω讨论其解形式

情况1：δω

特征根方程两相异实根,，其通解形式为：

情况2：δω

特征根方程一对相同实根，同为，其通解形式为:

情况3：δω

特征根方程实数域无根，复数域一对共轭复根：，，其通解形式为：

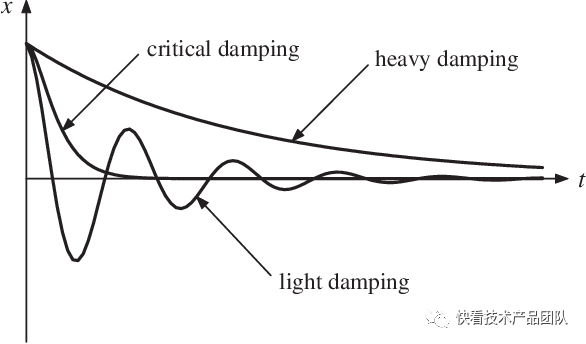
这三种分别对应阻尼震动的三种形式：过阻尼、临界阻尼和欠阻尼

过阻尼欠阻尼临界阻尼.png从用户体验角度讲，在不发生震荡的前提下反弹后以最快速度恢复到边界通常会获得最佳手感。因此在这里，苹果必然会选择临界阻尼为自己通用组件边界减震，因此我们选择临界阻尼条件δω下的通解形式：

此时δω，我们取δ，那么解特征根方程：λδλδ ，得到：λδω

将λ解带入替换通解的，得到:

δ根据初始条件：Bounces开始时,，得到，因此化简为：

δ、δ是两个待定系数，后面介绍测量方法，这里直接给出：是首次接触边界时的速度，δ是常数10.9，故Bounces公式为：

3.相关解释

特征根方程与微分方程的关系：

对于二阶齐次方程： ，考虑一个函数最容易凑出二阶导、一阶导、自身最容易提取出包含变量的公因式，并能够将剩余常数通过加减法抵消。

那么这个函数理应是指数函数，因为指数函数的导数总是能提取出自身：

如果确认了这种解形式，那么此方程可写为：

指数不可能为0，所以左侧多项式λλ的解λ即是微分方程的解，所以这个简化后的方程就是特征根方程。

4.结论

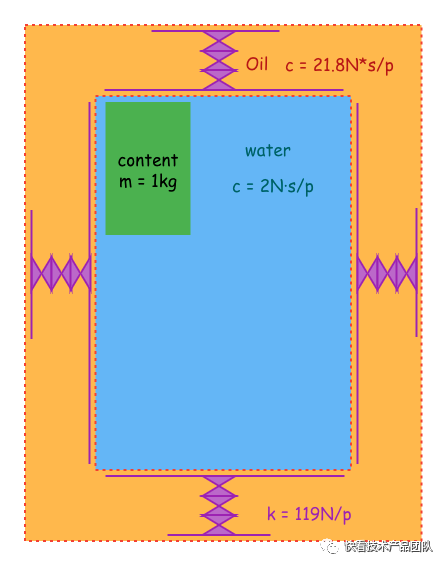
Bounces运动是一种阻尼震动，这种震动依赖的弹性k和阻尼满足了一种特殊的数量关系，使得Bounces遵循临界阻尼震动，从而呈现出一种“回弹永远不会弹过边界或发生反复震动”现象。经过以上讨论，我们尝试构建了一下UIScrollView的内容展示区的复原图如下：

Bounces俯视图.png

参数测量方法

由于存在、δ两个待定系数，而我们能观测到的数值主要是contentOffset，也就是位移，、δ 的影响因素是速度、加速度这种更高级别的参数，通过观察位移确定、δ难度较高，所以在这里我们使用一种简单的优化方法来让这我们预测的运动趋势与实际趋势逐渐吻合。

1.梯度下降思路

  1. 给定一组UIScrollView冲击边界触发Bounces的真实数据集合，内包含Bounces动画期间内所有的contentOffset取值：。
  2. 给定一组待定系数的解、δ、φ，通过公式φδφ 计算出所有的理论值。
  3. 计算出理论值与实际值的方差： ，函数越小，理论曲线与实际曲线的越接近。
  4. 如果我让、δ、φ中任意一个值，单独进行变化，能够让目标函数的值变小，那么就对这个变化予以肯定，将原值修改为变化后的值。对于三个待定系数，我们有六个方向进行变化，、、δδ、δδ、φφ、φφ，当这六中变化中有多种变化都可以让目标函数结果变小，那么我们取变得最小的那个变化，因此这个方法也叫最速下降法。
  5. 当目标函数被优化到0时，说明我们的目标曲线与实际观测出的曲线已经完全重合了；而我们机器上观测到的数值总是离散的，所以实际上，这个数值被优化到个位数时就已经非常接近了。

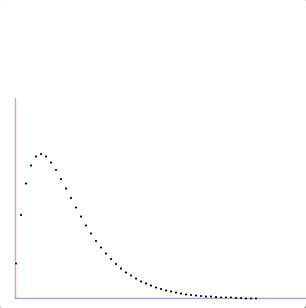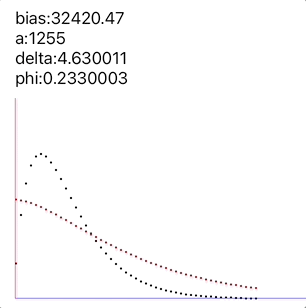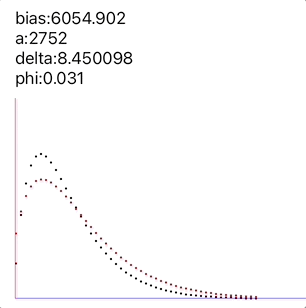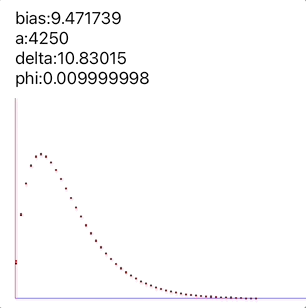
以下是一组Bounces数据的优化过程：

cMfdpt.gif

最终我们对多组类似上面的数据进行测量，δ 值总是接近于10.9的一个数；而 则根据每次Bounces的力度不同发生变化。

2.参数C的确定

由于我们发现了的大小受到每次Bounces的力度影响，因此找到了一个包含两种参数的关系探究具体的算法，利用这个公式：

是合力，是持续时间，由于合力中的弹力、阻力两部分随时间变化，因此这两部都被写成积分形式（小是阻尼系数，大是待固定的常数）

然后把上面那里拿到的、的公式：

δδδδ代入到左边那个积分里：

发现左边的积分里面总是能提取出来一个 ，里面就没有 了，只剩一堆已知的量，这个时候恰好右面有个，所以 和初速度 是呈正比的，比例系数就是m除以剩余的那一堆积分。不用算这个积分，我们只需要找到一组Bounces的数据，通过减速的规律得到，通过上面那个优化方法优化出此次Bounces与实际值最接近的，（上面动图里的第二个变量：），求出此次Bounces中与的比例就是所有情况下的固定比值，非常凑巧这个比值就是1。所以整体的算式就成为：

3.其他相关数值

劲度比：

阻尼比：

4.Bounces最远距离

根据 ，满足 的点即是最远处，得到：

δδδ得到:

δ，δ两个结论：

5.Bounces递推形式

考虑到我们自己实现一个CustomScrollView,在使用CADisplayLink执行Bounces动画时，已知的条件只有某个瞬间的瞬时速度和当前所在位置；而这个不一定0，也不一定是；所以在这里我们提供任意瞬时状态{}转的方法：

两式相除：

右侧等式化简的到t表达式：

δ带入y得到表达式：

δ这样，我们可以根据任意时刻的状态计算出完整的Bounces表达式和当前的时间t，然后,使用和的算式计算出下次刷新时候的，不断更新这个状态，就实现了UIScrollView一样Bounces变化。

实际开发中的用途

1.使用Decelerate在两个UIScrollView减传递能量

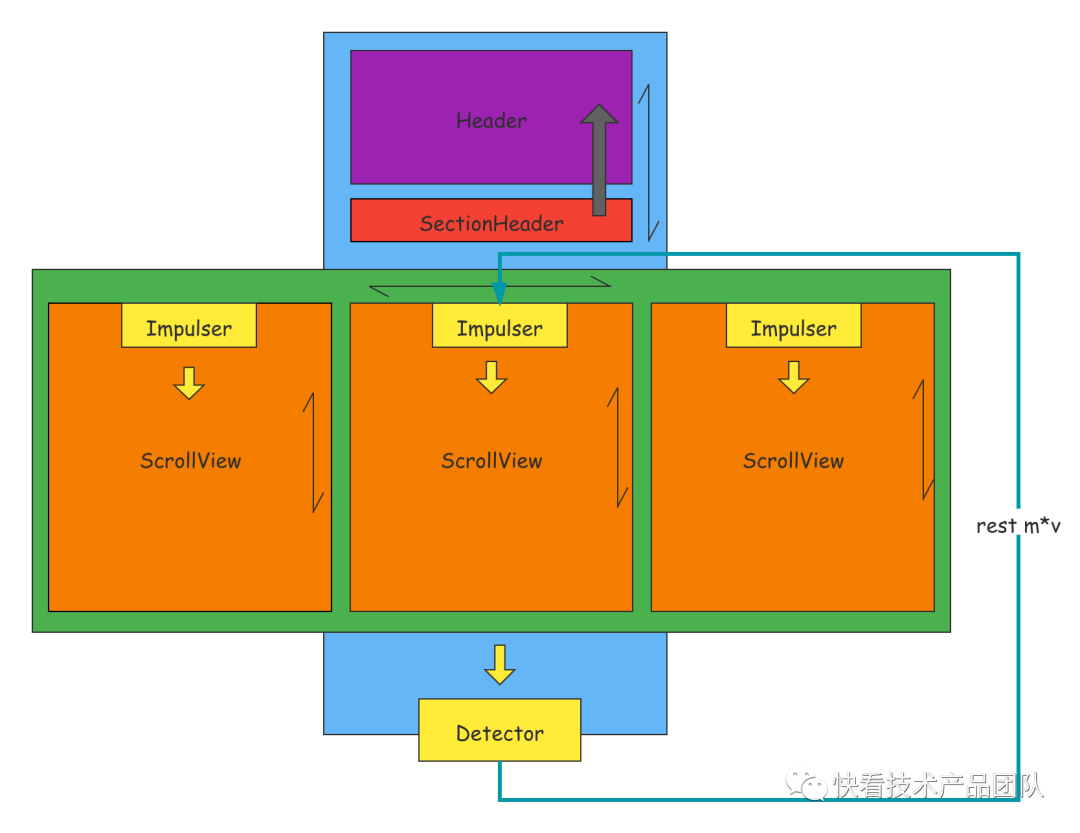
我们首次应用到Decelerate是在一次对漫画专题页的大改版中。该次改版，专题页采用了一种多层UIScrollView嵌套的复杂结构，这个结构的最外层是纵向的滚动视图，承载了头部、可吸顶区域，和分页容器三个部分；分页容器是一个横向的滚动视图；内部又分为多个纵向滚动视图，由此组成了三层嵌套UIScrollView，如下：

专题页结构.png

用户在头部和吸顶区域向上拖拽后生效的是最外层蓝色的纵向视图，当蓝色的层级触底后，会有一个明显的停顿效果；因为父视图的手势生效，剩余的惯性无法传递到内部的橘黄色纵向视图；为了弥补这部分缺陷，让整个纵向列表看起来更加融为一体，我们为外层的蓝色视图分配了一个剩余速度（或冲量）检测的机制：

Q：关于为什么传递A：我们为每个Detector和Impulser分配了额外的一个属性m，从而让这这些动效可以在二者之间以不同比例传递，这看起来就像：一个密度较大的球体撞向了一个密度较小的球体。通常状况下默认质量都是1，因此不同的UIScrollView之间的剩余速度会以1：1的比例传递。

2.使用Bounces实现POP类型弹幕

首次应用到Bounces动画是制作弹幕库时，由于平台特殊性，需要一种POP类型弹幕兼容漫画详情页弹幕播放，我们使用与Bounces类似的参数关系构建临界阻尼，使用此种曲线控制弹幕缩放：

POP.gif

为了节省性能，我们将几组配置好参数的临界阻尼曲线执行了间隔0.0167s的打点，并将这些点的数值存储在一个静态的数组中，弹幕轨道执行时直接从固定的几个数组中获取响应的数值，这样在使每个POP轨道中的弹幕均以相同的规律运行的同时，也不必去反复计算那些繁琐的指数，减少了普通POP动画执行时数值计算的大量性能消耗。

结语

苹果工程师们为开发者们构建和谐社会中处处透露着精致与优雅，作为iOS工程师的我们透过简单的几个接口和代理了解到其追求极致用户体验背后所付出的巨大努力。使用者只是轻轻触摸手机屏幕，即可在大海中畅快遨游；靠岸时又能体验到蹦床一般的新鲜与刺激感，别具一番风味；在充分享受刺激的同时，柔软的史莱姆将你身体充分包裹以免受任何伤害；人世间最大的快乐莫过于此

Copyright© 2013-2020

All Rights Reserved 京ICP备2023019179号-8