如何用 canvas 画出分形图
前言
分形是一门以非规则几何形态为研究对象的几何学,由曼德勃 罗(B.B.Mandelbrot)等人创立并命名。
分形图从整体上看,是处处不规律的。但从局部观察,图形的规则性又是相同的,即具有自相似的性质。
通常意义下,分形被定义为将一个确定的几何形状(元图像)在其边上迭代地生成为)与元图像近似地的形状。这次想用 canvas 画出典型的几个分形图。
基础数学篇
在画分形图之前我们需要首先明确 Canvas 的数学体系,才能利用好这个工具完成分型图的绘制。
众所周知,Canvas 采用的坐标系默认是以画布左上角为坐标原点,x 轴向右,y 轴向下。画布的大小决定了坐标系 x、y 轴的最大值。
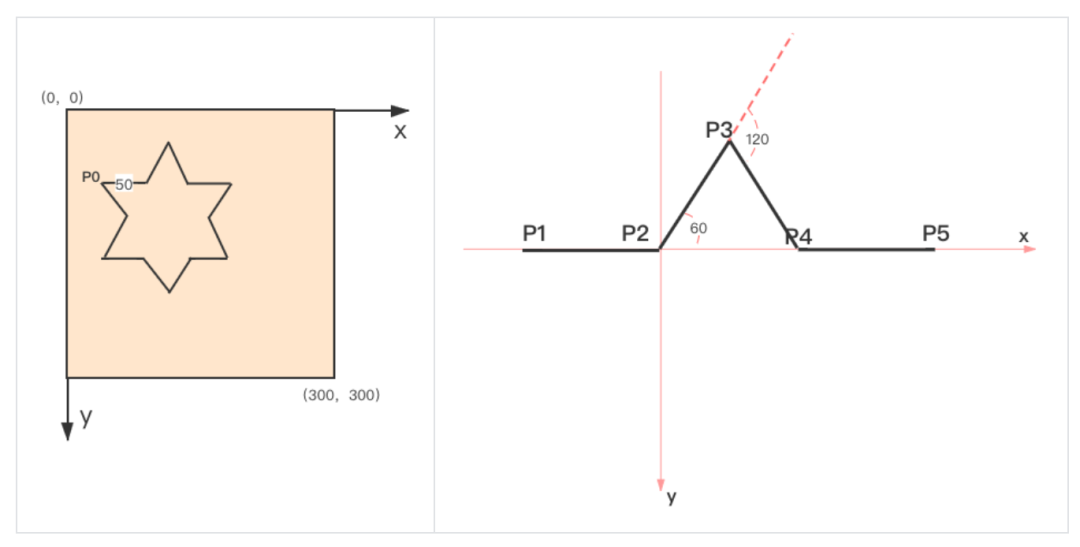
假设,我们要在宽 300 * 高 300 的一个 Canvas 画布上实现一个六角形。其中,六角形的边长是 50。试想应该怎么做。
观察六角形的基本形状,找到 12 条边的规律是:相邻两条边为一组,第 1 条边画完后逆时针转 60 度,画完相同长度的第 2 条边,随后顺时针转 120 度,这样重复执行 6 次后,一个基础的六角形就画出来了。
旋转与坐标点映射
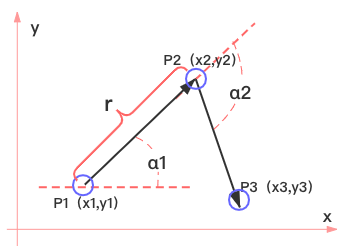
先简单复习一下数学知识。已知 P1、P2 的坐标,P2P1 的长度为 r,将向量 P1P2 顺时针旋转 α2 角度后,计算 P3 的坐标值。
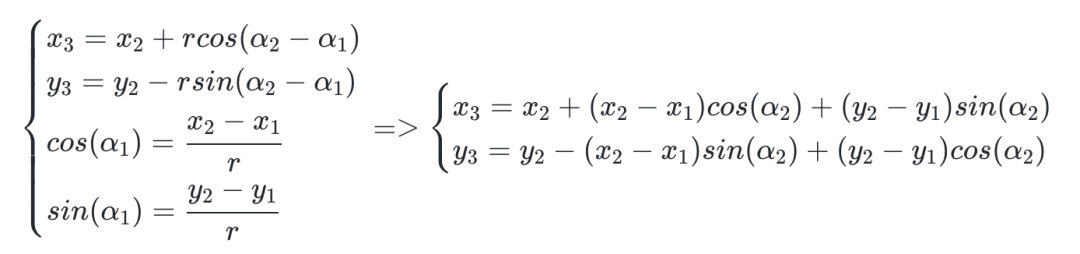
顺时针ββββ[cosβ−sinβsinβcosβ]逆时针ββββ[cosβsinβ−sinβcosβ]
代码实现
- 绘制六角形。首先从第一个点P1(0,50)、P2(50,50)开始画,核心模块放入hexagon方法中,迭代6次。
var ctx = canvas.getContext("2d"); ctx.strikeStyle = "#000"; ctx.beginPath(); const y = 50; ctx.moveTo(0, y); hexagon(ctx, 0, y, 50, y, 0, 6);
2 . hexagon 方法的输入参数有(ctx, x1, y1, x2, y2, n, m)。
function hexagon(ctx, x1, y1, x2, y2, n, m) {
ctx.clearRect(0, 0, 300, 300);
// 顺时针 60度
ctx.moveTo(x2, y2);
const x3 = x2 +
(x2 - x1) * Math.cos(Math.PI / 3) +
(y2 - y1) * Math.sin(Math.PI / 3);
const y3 = y2 -
(x2 - x1) * Math.sin(Math.PI / 3) +
(y2 - y1) * Math.cos(Math.PI / 3);
ctx.lineTo(x3, y3);
// 逆时针 120度
const x4 = x3 +
(x3 - x2) * Math.cos((Math.PI * 2) / 3) -
(y3 - y2) * Math.sin((Math.PI * 2) / 3);
const y4 = y3 +
(y3 - y2) * Math.cos((Math.PI * 2) / 3) +
(x3 - x2) * Math.sin((Math.PI * 2) / 3);
ctx.lineTo(x4, y4);
ctx.stroke();
n++;
if (n === m) {
return false;
} else {
hexagon(ctx, x3, y3, x4, y4, n, m);
}
}向量运算
从以上流程可以看出,通过坐标进行点的绘制是非常麻烦并且费时间的,加上 Canvas 2D 的坐标与常规数据坐标系上下颠倒,我们会花费大量时间在坐标点的计算上。
因此,为了代码的逻辑简单、易读,我们可以转变思路,将坐标点以向量的方式来理解。复习一下常用的向量运算有以下几种。
向量相加/减。向量点乘、叉乘。如图 1 所示,向量相加的含义是,路径沿 v1、v2 进行绘画,则 P2 坐标点为 v1 与 v2 两个向量相加,为[x1+x2, y1+y2]。点乘为 a、b 向量点积的几何含义,是 a 向量乘以 b 向量在 a 向量上的投影分量,如图 2 所示。叉乘为两向量组成的面积,如图 3 所示。
代码实现
用形如 [x,y] 的数组方式描述向量。
class Vector extends Array {
constructor(x = 1, y = 0) {
super(x, y);
}
copy() {
return new Vector(this.x, this.y);
}
}向量相加减。
add(v) {
this.x += v.x;
this.y += v.y;
return this;
}
sub(v) {
this.x -= v.x;
this.y -= v.y;
return this;
}向量叉乘点乘。
cross(v) {
return this.x * v.y - v.x * this.y;
}
dot(v) {
return this.x * v.x + v.y * this.y;
}向量旋转。
rotate(rad) {
const c = Math.cos(rad),
s = Math.sin(rad);
const [x, y] = this;
this.x = x * c + y * -s;
this.y = x * s + y * c;
return this;
}按照向量运算,画出一个六角雪花的代码可以改写成以下方式。首先将 canvas 坐标系进行上下翻转,形成我们习惯的坐标方式。
var ctx = canvas.getContext("2d");
ctx.translate(0, canvas.height);
ctx.scale(1, -1);得到 v0、v1 的向量,进行逆时针和顺时针的旋转,得到的效果与之前的方式一致,但代码的可读性却增加了很多。
const v0 = new Vector(0, 250);
const v1 = new Vector(50, 250);
hexagon(ctx, v0, v1, 0, 6);
function hexagon(ctx, v0, v1, n, m) {
const v2 = v1.copy().sub(v0);
v2.rotate((60 * Math.PI) / 180).add(v1); // 逆时针 60度
const v3 = v2.copy().sub(v1);
v3.rotate((-120 * Math.PI) / 180).add(v2); // 顺时针 120度
ctx.beginPath();
ctx.moveTo(...v1);
ctx.lineTo(...v2);
ctx.lineTo(...v3);
ctx.stroke();
n++;
if (n === m) {
return false;
} else {
hexagon(ctx, v2, v3, n, m);
}
}实践篇
分形图的逻辑规律是递归与基础图形的结合,在实践篇中我们选择几个典型分形图进行实现。
科赫雪花
科赫雪花最早由数学家 Helge von Koch 提出,是分形几何中经典图像之一。它的生成基于科赫曲线,即单边的无限分形。
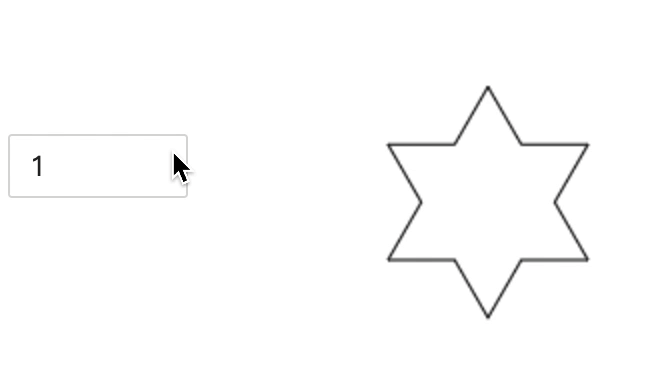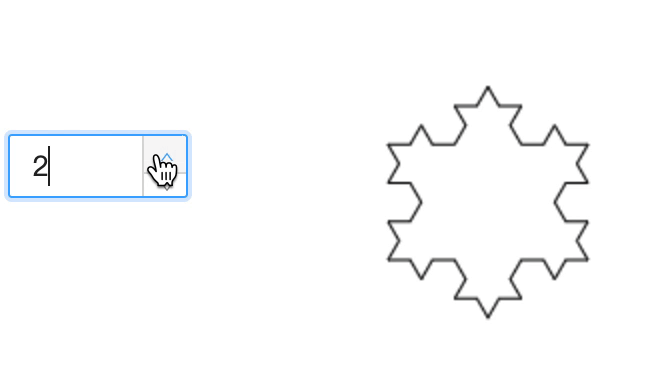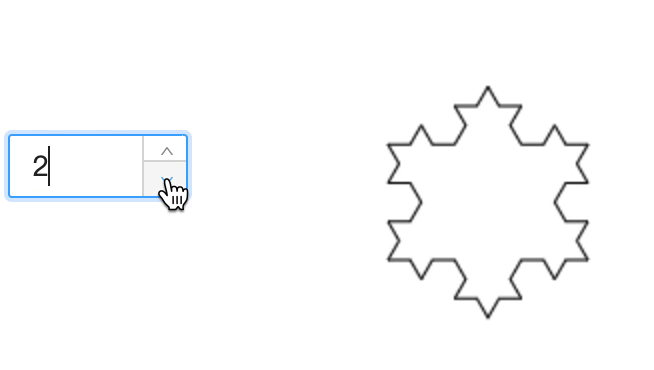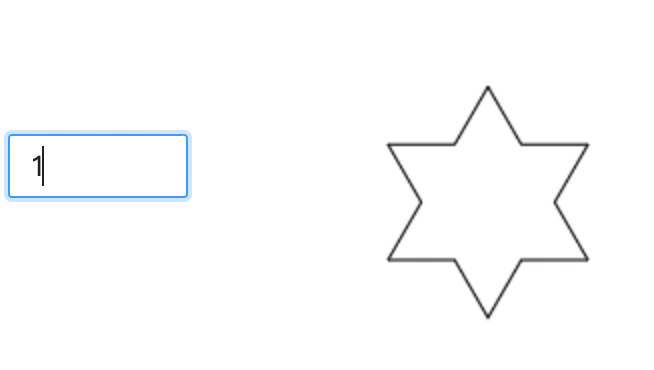
先看一下实现效果,它的基础图形是等边三角形。该图片的面积有限,但周长是无限的。每次迭代,线段的长度都会增加原长度的三分之一。


思路
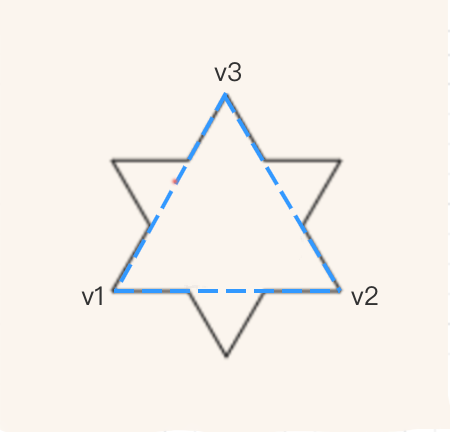
- 科赫雪花由科赫曲线组成,它最基本的形状是一个三角形,将三角形的每条边等分成 3 份,中间那份线段先右转 60 度之后画出边长一样的线段后,再向左旋转 120 度画出等长。
- 在递归的模块里递归执行步骤 1,直到达到设置的递归层级。
代码实现
首先还是坐标变换,将坐标原点从左上角移动到左下角,并且让 y 轴翻转为向上。
var ctx = canvas.getContext("2d");
ctx.translate(0, canvas.height);
ctx.scale(1, -1);然后我们找到三角形的三个顶点,假设我们从 v1(100,100)出发,三角形边长为 100,则通过向量变换可以获取其余两个顶点 v2、v3 向量。
var ctx = canvas.getContext("2d");
const v1 = new Vector(100, 100);
const v2 = new Vector(100, 0).add(v1);
const v3 = new Vector(100, 0).rotate((60 * Math.PI) / 180).add(v1);接着我们根据对三条边,也就是 v1v2、v2v3、v3v2 三向量分别进行递归操作。
koch(ctx, v1, v2, 0, deep);
koch(ctx, v2, v3, 0, deep);
koch(ctx, v3, v1, 0, deep);我们定义一个递归的核心模块:function koch(ctx, v1, v2, n, m) {}
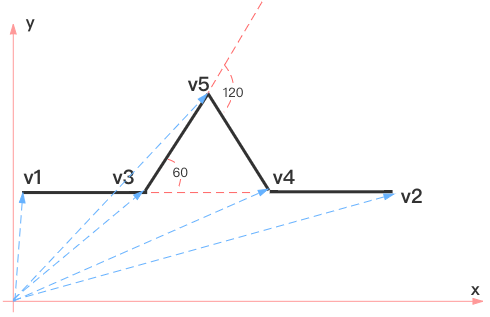
该函数有五个参数:ctx 是 Canvas2D 上下文。v1 是一条边的起始向量,v2 是终止向量,n 为当前迭代层级,m 为总共迭代次数。在模块中我们根据图 5 中描述,将一条边划分成四段,每段长度相同。得到 v3、v4、v5。终止条件为迭代层级与规定好的次数相同,这时将 v1~v5 的折线路径连接起来。这样就形成了一个科赫雪花。代码如下。
function koch(ctx, v1, v2, n, m) {
ctx.clearRect(0, 0, 300, 300); //每次绘图前清除画板
const oneThirdVector = v2
.copy()
.sub(v1)
.scale(1 / 3);
const v3 = oneThirdVector.copy().add(v1);
const v4 = oneThirdVector.copy().scale(2).add(v1);
const v5 = v4
.copy()
.sub(v3)
.rotate((-60 * Math.PI) / 180)
.add(v3);
n++;
if (n === m) {
//绘图(连线) 当前层级与设定层级一致时候停止递归
ctx.moveTo(...v1);
ctx.lineTo(...v3);
ctx.lineTo(...v5);
ctx.lineTo(...v4);
ctx.lineTo(...v2);
ctx.stroke();
return false;
}
//递归调用绘图
koch(ctx, v1, v3, n, m);
koch(ctx, v3, v5, n, m);
koch(ctx, v5, v4, n, m);
koch(ctx, v4, v2, n, m);
}六角形雪花
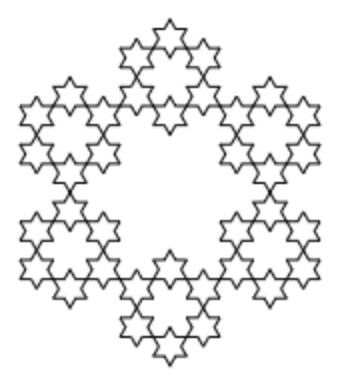
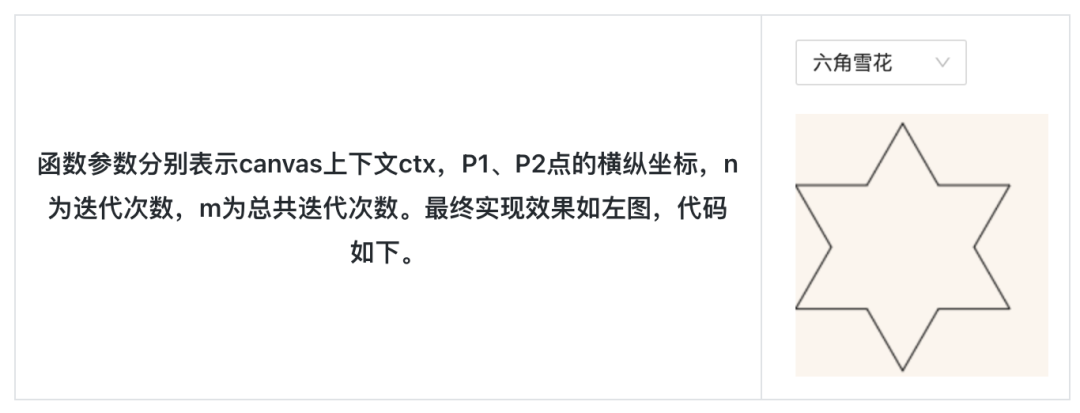
先看一下实现效果,它的基础图形是六角形。每迭代一次,都以每条线段的 1/3 作为边长,在每个角顶点处再画出下一个小六角形。重复这个步骤便可以得到一个六角形雪花分型图。



思路
- 首先根据基础篇中提到的六角形雪花的生成规律,每相邻两条边为一组,第 1 条边左转 60 度,第 2 条边右转 120 度,执行 6 次即可得到基础形状六角形。
- 在开始画线之前判断该次的边长是否小于规定的最小边长。如果不小于则将边长变为原变成的 1/3,进行递归调用,若小于则开始绘制六角形。
代码实现
坐标变化和获取 canvas 2D 的上下文这里就不再累述。首先,我们从 v0、v1 出发进行画六边形的主函数中。
const v0 = new Vector(50, 200);
const v1 = new Vector(100, 200);
hexagon(ctx, v0, v1);我们定义一个递归的核心模块:function hexagon(ctx, v0, v1) {}
该函数有五个参数:ctx 是 Canvas2D 上下文。v0v1 是开始作画的起始向量,也就是给我们的作画一个开始的方向。hexagon 中,我们计算出本次迭代的六角形边长hexagonLen,当不满足终止条件时候进行迭代。
function hexagon(ctx, v0, v1) {
const hexagonLen = v1.copy().sub(v0).vlength;
if (hexagonLen > minLine) {
// 进入迭代
}
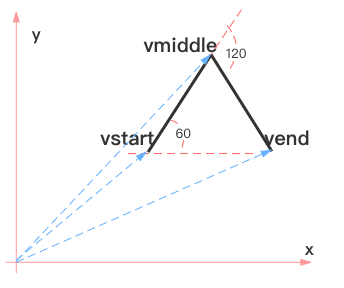
}这里我们将六角形分为 6 次循环。每次循环都是从 vstart 到 vmiddle,再到 vend。
// 迭代中 hexagon(ctx, v0, v1)
let vstart = v1.copy();
let vmiddle = v1.copy().sub(v0);
let vend = new Vector();
for (let i = 0; i < 6; i++) {
// 六角形的6次循环
}在循环体中,我们先获取该次迭代中 vstart、vmiddle、vend 的向量,以及下一次的边长。如果新的边长大于设置的最小边长minLine,则进行下一次的迭代,否则,便沿着这三个向量进行绘制。绘制完后,更新 vstart、vmiddle。
// 向量旋转
vmiddle.rotate((60 * Math.PI) / 180).add(vstart);
vend = vmiddle.copy().sub(vstart);
vend.rotate((-120 * Math.PI) / 180).add(vmiddle);
const thirdv = vend
.copy()
.sub(vmiddle)
.scale(1 / 3)
.add(vmiddle);
const newHexagonLen = thirdv.copy().sub(vmiddle).vlength;
if (newHexagonLen > minLine) {
// 递归
hexagon(ctx, vmiddle, thirdv);
} else {
// 绘图
ctx.beginPath();
ctx.moveTo(...vstart);
ctx.lineTo(...vmiddle);
ctx.lineTo(...vend);
ctx.stroke();
}
vstart = vend.copy();
vmiddle = vend.copy().sub(vmiddle);这样,我们就实现了绘制六角雪花的方法。
二叉树
实现一颗二叉树要比前面的科赫雪花和六角形雪花简单的多。
思路
- 首先我们只需要知道初始状态时的起点以及树干的长度。
- 在递归模块中,我们将树枝长度与宽度都削减为上一级树枝的 1/2。并且进行固定角度的左右偏移。终止条件为树枝的长度小于规定好的最小长度。这样就可以画出一颗二叉树了。


代码实现
这里就不讲解代码了,有兴趣的同学可以点击这里进行代码访问。
总结
在绘制分形图的过程中,我们复习了以下几个知识点,首先,在 Canvas 中我们可以通过坐标系变换来满足实际需求,对坐标进行合理的变化可以让我们的绘图逻辑变得简单易懂。其次,向量在可视化中是非常方便且基础的工具,掌握和学会用向量的思维计算是学习可视化的必经之路。最后,分形图大多数都是元图像加迭代的方式,练习分形图的绘制也有助于我们掌握各式各样的递归操作,以及总结出此类图形的逻辑方法。
参考资料
[1]这里: https://codesandbox.io/s/canvas-tree-hhjoh?file=/src/components/Tree.jsx
[2]canvas生成科赫雪花(曲线): https://garychang.cn/2017/01/06/koch/
[3]GitHub - akira-cn/graphics: 一些图形系统相关的小例子: https://github.com/akira-cn/graphics
[4]二维旋转矩阵与向量旋转: https://zhuanlan.zhihu.com/p/98007510
[5]canvas fenxing - CodeSandbox: https://codesandbox.io/s/canvas-fenxing-hhjoh
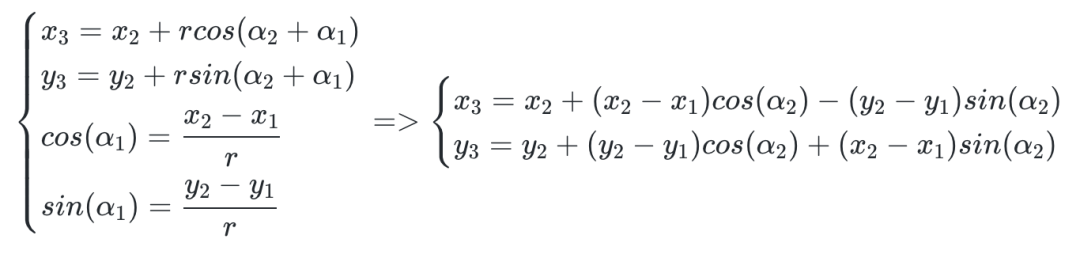
![x1+x2, y1+y2]。点乘为a、b 向量点积的几何含义,是 a 向量乘以 b 向量在 a 向量上的投影分量,如图2所示。叉乘为两向量组成的面积,如图3所示。