位程序员们，大家好！

很多程序员一遇到算法问题就头大，避之不及。其实不用怕，算法只是解决问题的步骤而已。

今天就让我们以简单和说明性的方式介绍一些主要算法。

理解 Big O Notation

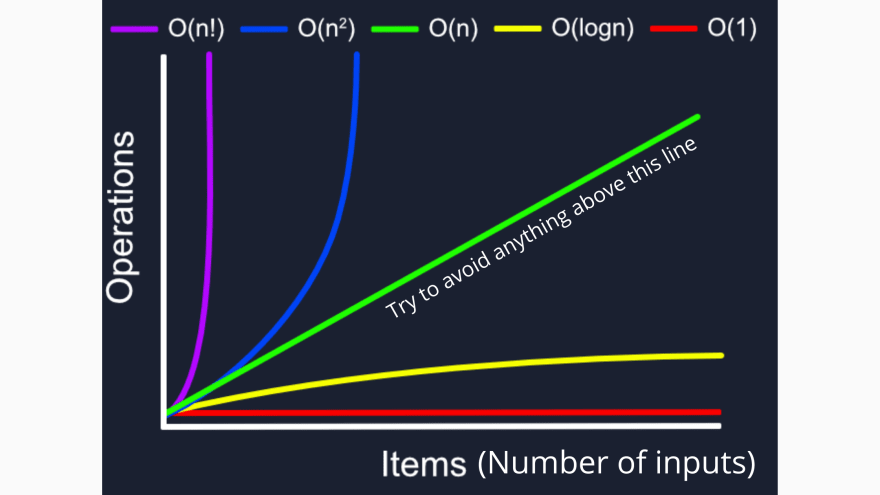
Big O Notation是一种表示算法的时间和空间复杂度的方法。

• 时间复杂度：算法完成执行所花费的时间。
• 空间复杂度：算法占用的内存。

表示算法时间复杂度的表达式（符号）不多。

• O(1)：恒定时间复杂度。这是理想情况。
• O(log n)：对数时间复杂度。如果log(n) = x那么它与10^x相同。
• O(n)：线性时间复杂度。时间随着输入的数量呈线性增加。例如，如果一个输入需要1ms，那么4个输入需要4ms来执行算法。
• O(n^2)：指数时间复杂度。主要发生在嵌套循环的情况下。
• O(n!)：阶乘时间复杂度。这是最坏的情况，应避免。

你编写的算法应该尽量用前3个时间复杂度表示。最后两个应该尽可能避免。

如果你想尽可能降低复杂性，那么最好避免任何高于O(n)的情况。

算法

什么是算法，为什么我们要关心算法？

解决问题的方法或说解决问题的步骤、程序或规则集称为算法。

例如：搜索引擎算法用于查找与搜索字符串相关的数据。

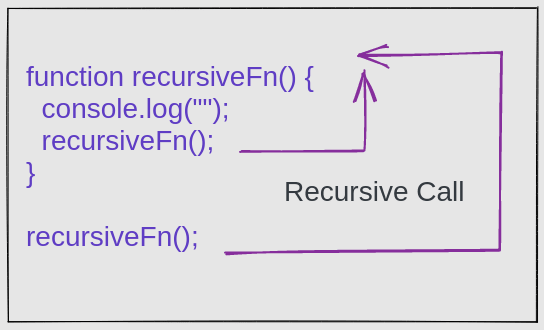
递归

调用自身的函数就是递归。你可以将其视为循环的替代方案。

function recursiveFn() {
    console.log("This is a recursive function");
    recursiveFn();
}

recursiveFn();

请看上述代码片段的第3行，recursiveFn调用了recursiveFn本身。这就是我之前提到的，递归是循环的替代方法。

那么，这个函数到底要运行多少次呢？

没错，这将创建一个无限循环。

假设我们只需要运行循环10次。在第11次返回迭代函数。即停止循环。

let count = 1;
function recursiveFn() {
    console.log(`Recursive ${count}`);
    if (count === 10) return;
    count++;
    recursiveFn();
}

recursiveFn();

在上面的代码片段中，第4行返回并在count 10处停止循环。

现在看一个更现实的例子：从给定的数组中返回奇数数组。实现方法很多，包括for-loop、Array.filter方法等。

但是为了展示递归的用法，这里使用helperRecursive函数。

function oddArray(arr) {
    let result = [];
    function helperRecursiveFn(arr) {
        if(arr.length === 0) {
            return; // 1
        } else if(arr[0] % 2 !== 0) {
            result.push(arr[0]); // 2
        }
        helperRecursiveFn(arr.slice(1)); // 3
    }
    helperRecursiveFn(arr);
    return result;
}

oddArray([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]);
// OutPut -> [1, 3, 5, 7, 9]

这里的递归函数是helperRecursiveFn。

1. 如果数组长度为0，则返回。
2. 如果元素是奇数，则将元素推送到result数组。
3. 使用切片数组的第一个元素调用helperRecursiveFn。每次都会切片数组的第一个元素，因为已经检查过它是奇数还是偶数。

例如：第一次用[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]调用helperRecursiveFn。下一次将用[2, 3, 4, 5, 6, 7, 8, 9, 10]调用helperRecursiveFn，直到数组长度为0。

线性搜索算法

线性搜索算法非常简单。假设你需要查找给定数组中是否存在数字。

运行简单的for循环并检查每个元素，直到找到要查找的元素即可。

const array = [3, 8, 12, 6, 10, 2];

// Find 10 in the given array.
function checkForN(arr, n) {
    for(let i = 0; i < array.length; i++) {
        if (n === array[i]) {
            return `${true} ${n} exists at index ${i}`;
        }
    }

  return `${false} ${n} does not exist in the given array.`;
}

checkForN(array, 10);

这就是线性搜索算法。将以线性方式逐个搜索数组中的每个元素。

线性搜索算法的时间复杂度

只有一个运行n次的for循环。其中n在最坏的情况下是给定数组的长度。迭代次数在最坏的情况下与输入（即数组的长度）成正比。

因此线性搜索算法的时间复杂度是线性时间复杂度：O(n)。

二分搜索算法

在线性搜索中，我们一次只能消除一个元素。但是二分搜索算法允许我们一次消除多个元素。这就是二分搜索比线性搜索快的原因。

这里要注意的一点是二分搜索仅适用于排好序的数组。

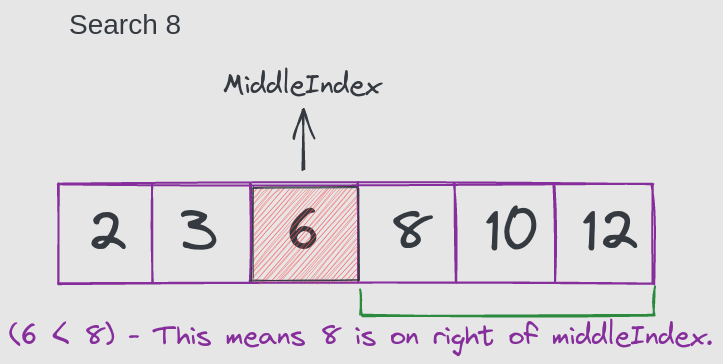
该算法遵循分而治之的方法。例如，我们要在[2, 3, 6, 8, 10, 12]中查找8的索引。

第1步：

找到数组的middleIndex。

const array = [2, 3, 6, 8, 10, 12];
let firstIndex = 0;
let lastIndex = array.length - 1;
let middleIndex = Math.floor((firstIndex + lastIndex) / 2); // middleIndex -> 2

第2步：

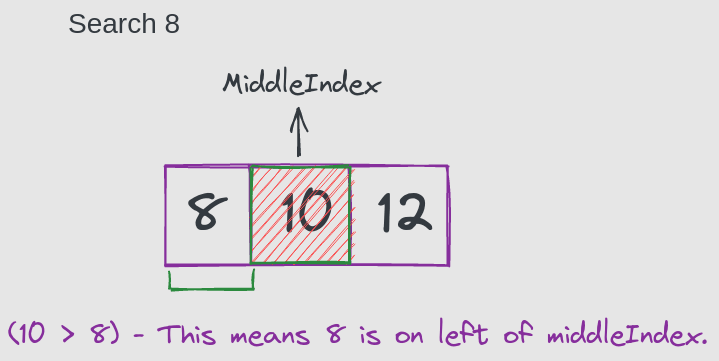
检查middleIndex元素是否大于8。如果是，则表示8在middleIndex的左侧。然后将lastIndex更改为middleIndex - 1。

第3步：

反之，如果middleIndex元素小于8。意味着8在middleIndex的右侧。那么将firstIndex更改为middleIndex + 1。

if (array[middleIndex] > 8) {
    lastIndex = middleIndex - 1;
} else {
    firstIndex = middleIndex + 1;
}

第4步：

每次迭代都会根据新的firstIndex或lastIndex再次设置middleIndex。

让我们通过代码总和所有步骤。

function binarySearch(array, element) {
    let firstIndex = 0;
    let lastIndex = array.length - 1;
    let middleIndex = Math.floor((firstIndex + lastIndex) / 2);

    while (array[middleIndex] !== element && firstIndex <= lastIndex) {
        if(array[middleIndex] > element) {
                lastIndex = middleIndex - 1;
        }else {
                firstIndex = middleIndex + 1;
        }
        middleIndex = Math.floor((firstIndex + lastIndex) / 2);
    }
    return array[middleIndex] === element ? middleIndex : -1;
}

const array = [2, 3, 6, 8, 10, 12];
binarySearch(array, 8); // OutPut -> 3

下面请看上述代码的可视化表示。

第1步

firstIndex = middleIndex + 1;

第2步

lastIndex = middleIndex - 1;

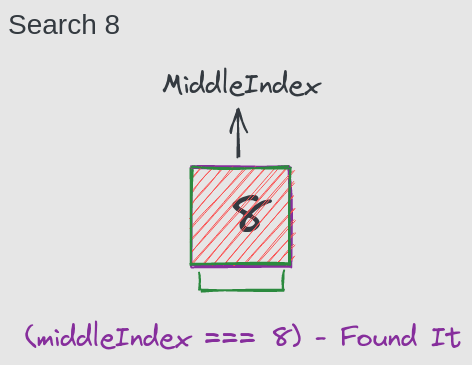
第3步

array[middleIndex] === 8 // Found It

二分搜索的时间复杂度

只有一个运行n次的while循环。但迭代次数不依赖于输入（数组长度）。

因此二分搜索算法的时间复杂度是对数时间复杂度：O(log n)。从O-notation图上我们可以知道，O(log n)比O(n)快。

朴素搜索算法

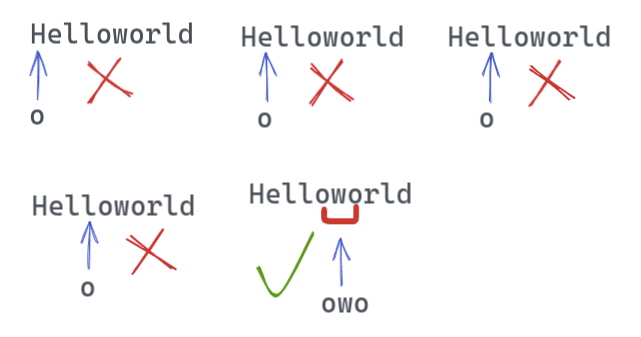
朴素搜索算法用于查找字符串是否包含给定的子字符串。例如，检查helloworld是否包含子字符串owo。

1. 主字符串（helloworld）运行第一个循环。
2. 在子字符串（owo）上运行嵌套循环。
3. 如果字符不匹配，则中断内部循环，否则继续循环。
4. 如果内循环完成并匹配，则返回true否则继续外循环。

可视化表示如下。

代码实现如下。

function naiveSearch(mainStr, subStr) {
    if (subStr.length > mainStr.length) return false;

    for(let i = 0; i < mainStr.length; i++) {
       for(let j = 0; j < subStr.length; j++) {
            if(mainStr[i + j] !== subStr[j]) break;
            if(j === subStr.length - 1) return true; 
        }
    }
    return false;
}

现在，让我们试着理解上面的代码。

• 第2行，如果子字符串的长度大于主字符串的长度，则返回false。
• 第4行，主字符串开始循环。
• 第5行，子字符串开始嵌套循环。
• 第6行，如果没有找到匹配项，则中断内循环，进行外循环的下一次迭代。
• 第7行，内循环的最后一次迭代返回true。

朴素搜索的时间复杂度

循环内有循环（嵌套循环），两个循环都运行n次。因此，朴素搜索算法的时间复杂度为（n * n），即指数时间复杂度：O(n^2)。

前面说过，如果可能的话，时间复杂度应该避免超过O(n)。所以下一个算法中我们将看到一种时间复杂度更低的好方法。

KMP算法

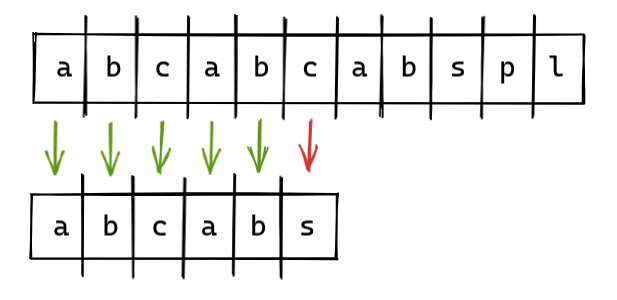
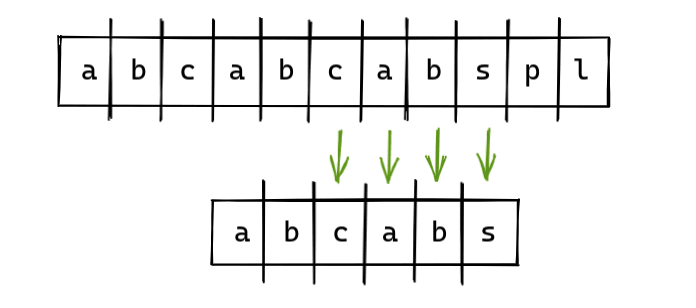
KMP算法是一种模式识别算法，有点难理解。好的，假设我们要在字符串abcabcabspl中查找是否包含子字符串abcabs。

如果我们用朴素搜索算法来解决这个问题，那么将匹配前5个字符不包括第6个字符。所以我们将不得不在下一次迭代中重新开始，并将失去上一次迭代的所有进度。

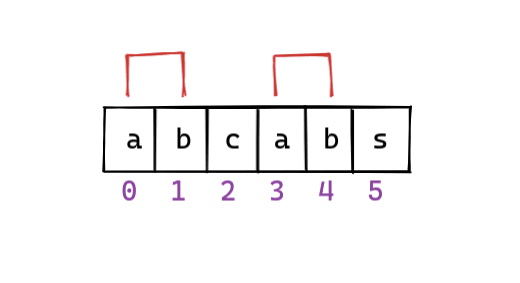
所以，为了保存进度，我们必须使用LPS表。现在在匹配的字符串abcab中，查找最长的相同前缀和后缀。

在字符串abcab中，ab是最长的相同前缀和后缀。

现在，我们将从索引5（对于主字符串）开始下一次搜索迭代。从之前的迭代中保存了两个字符。

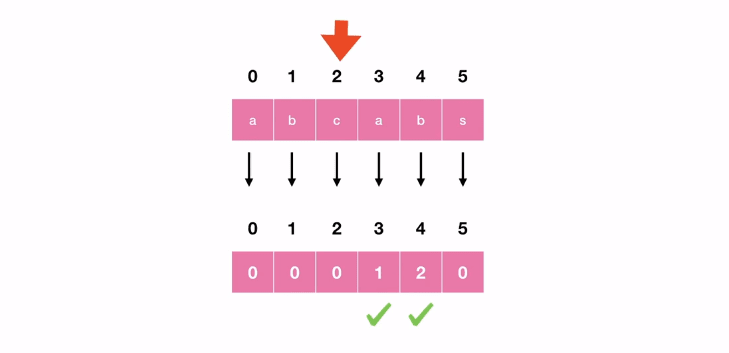
为了找出前缀、后缀以及从哪里开始下一次迭代，我们使用LPS表。

子字符串（abcabs）的LPS是0 0 0 1 2 0。

以下是计算LPS表的方法。

function calculateLpsTable(subStr) {
    let i = 1;
    let j = 0;
    let lps = new Array(subStr.length).fill(0);

    while(i < subStr.length) {
        if(subStr[i] === subStr[j]) {
            lps[i] = j + 1;
            i += 1;
            j += 1;
        } else {
            if(j !== 0) {
                j = lps[j - 1];
            } else {
                i += 1;
            }
        }
    }
    return lps;
}

使用LPS表的代码实现。

function searchSubString(string, subString) {
    let strLength = string.length;
    let subStrLength = subString.length;
    const lps = calculateLpsTable(subString);

    let i = 0;
    let j = 0;

    while(i < strLength) {
        if (string[i] === subString[j]) {
            i += 1;
            j += 1;
        } else {
            if (j !== 0) {
                j = lps[j - 1];
            } else {
                i += 1;
            }
        }
        if (j === subStrLength) return true;
    }

    return false;
}

KMP算法的时间复杂度

只有一个运行n次的循环。因此KMP算法的时间复杂度是线性时间复杂度：O(n)。

显而易见，与朴素搜索算法相比，KMP算法的时间复杂度明显改善。

冒泡排序算法

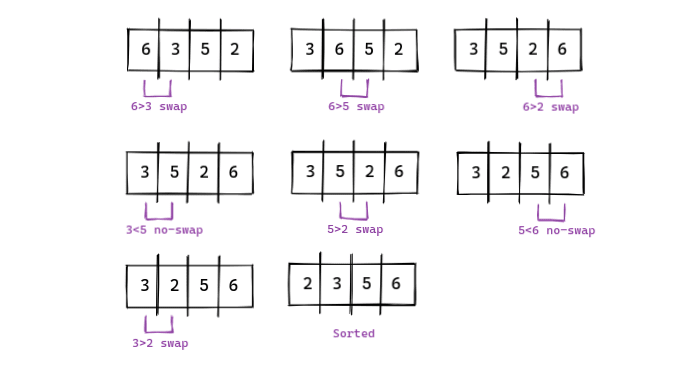
排序就是按升序或降序重新排列数据。冒泡排序是众多排序算法中的一种。

冒泡排序算法会将每个数字与前一个数字进行比较，并将较大的数字交换到后面。可视化表示如下。

冒泡排序的代码实现。

function bubbleSort(array) {
    let isSwapped;

    for(let i = array.length; i > 0; i--) {
        isSwapped = false;

        for(let j = 0; j < i - 1; j++) {
            if(array[j] > array[j + 1]) {
                [array[j], array[j+1]] = [array[j+1], array[j]];
                isSwapped = true;
            }
        }

        if(!isSwapped) {
            break;
        }
    }
    return array;
}

在上面的代码中：

• 通过变量i从数组的末尾向开头循环。
• 使用变量j开始内循环，直到(i - 1)。
• 如果array[j] > array[j + 1]，则两者交换。
• 返回已排序的数组。

冒泡排序算法的时间复杂度

因为有一个嵌套循环，并且两个循环都运行了n次，所以该算法的时间复杂度为(n * n)，即指数时间复杂度：O(n^2)。

归并排序算法

归并排序算法遵循分而治之的方法。这是两件事的组合——合并和排序。

在这个算法中，我们首先将主数组划分为多个单独的排序数组。

然后将单独排序的元素合并到最终数组中。

合并排序数组

function mergeSortedArray(array1, array2) {
    let result = [];
    let i = 0;
    let j = 0;

    while(i < array1.length && j < array2.length) {
        if(array1[i] < array2[j]) {
            result.push(array1[i]);
            i++;
        } else {
            result.push(array2[j]);
            j++;
        }
    }

    while (i < array1.length) {
        result.push(array1[i]);
        i++;
    }

    while (j < array2.length) {
        result.push(array2[j]);
        j++;
    }

    return result;
}

上面的代码将两个已排序的数组合并为一个新的排序数组。

归并排序算法

function mergeSortedAlgo(array) {
    if(array.length <= 1) return array;

    let midPoint = Math.floor(array.length / 2);
    let leftArray = mergeSortedAlgo(array.slice(0, midPoint));
    let rightArray = mergeSortedAlgo(array.slice(midPoint));

    return mergeSortedArray(leftArray, rightArray);
}

上述算法使用递归来将数组划分为多个单元素数组。

归并排序算法的时间复杂度

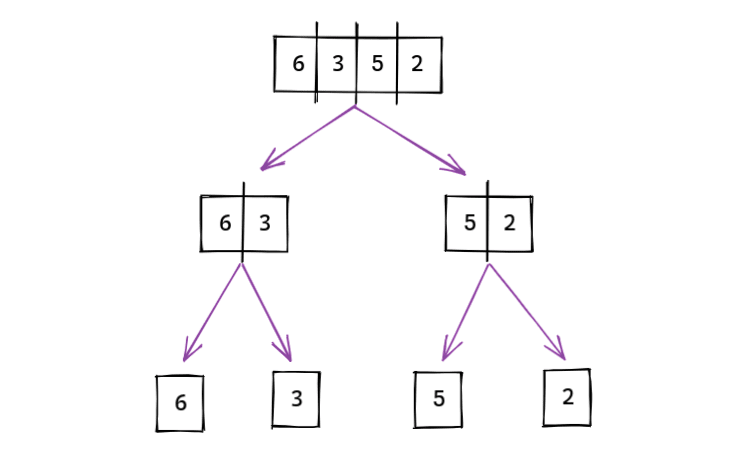
以之前的示例[6, 3, 5, 2]为例，将其划分为多个单元素数组需要2步。

现在，如果将数组的长度加倍（变成8），则需要3个步骤来划分(2^3)。也就是说，数组长度加倍并没有使步骤加倍。

因此归并排序算法的时间复杂度是对数时间复杂度：O(log n)。

快速排序算法

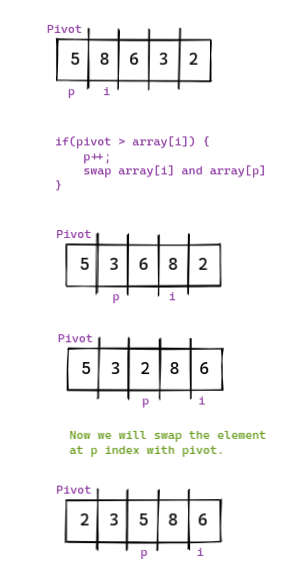
快速排序是最快的排序算法之一。在快速排序中，我们选择一个称为枢轴的单个元素，并将小于枢轴的所有元素移动到枢轴的左侧。

可视化表示如下：

对数组重复此过程，不断地将元素移到枢轴的左侧和右侧，直到完成排序。

代码实现

function pivotUtility(array, start=0, end=array.length - 1) {
    let pivotIndex = start;
    let pivot = array[start];

    for(let i = start + 1; i < array.length; i++) {
        if(pivot > array[i]) {
            pivotIndex++;
            [array[pivotIndex], array[i]] = [array[i], array[pivotIndex]];
        }   
    }

    [array[pivotIndex], array[start]] = [array[start], array[pivotIndex]];
    return pivotIndex;
}

上面的代码标识了枢轴的正确位置并返回位置索引。

function quickSort(array, left=0, right=array.length-1) {
    if (left < right) {
        let pivotIndex = pivotUtility(array, left, right);
        quickSort(array, left, pivotIndex - 1);
        quickSort(array, pivotIndex + 1, right);
    }

    return array;
}

上面的代码使用递归来不断移动枢轴到正确位置。

快速排序算法的时间复杂度

最佳情况：对数时间复杂度：O(n log n)

平均情况：对数时间复杂度：O(n log n)

最坏情况：O(n^2)

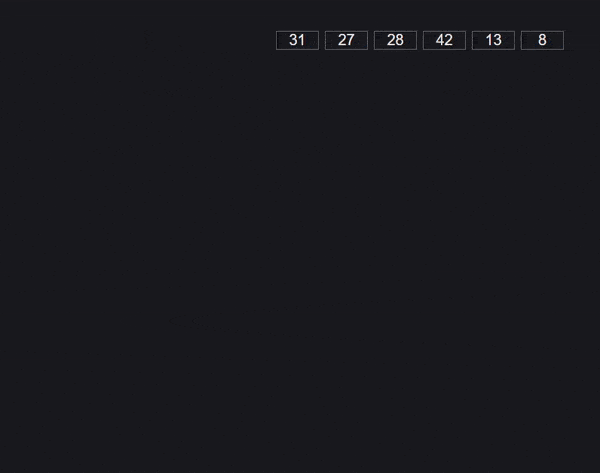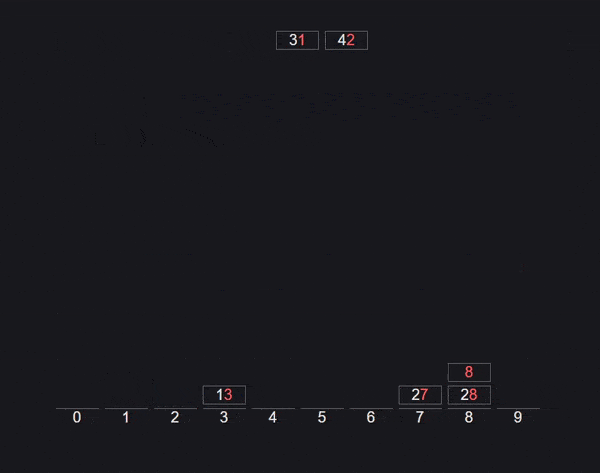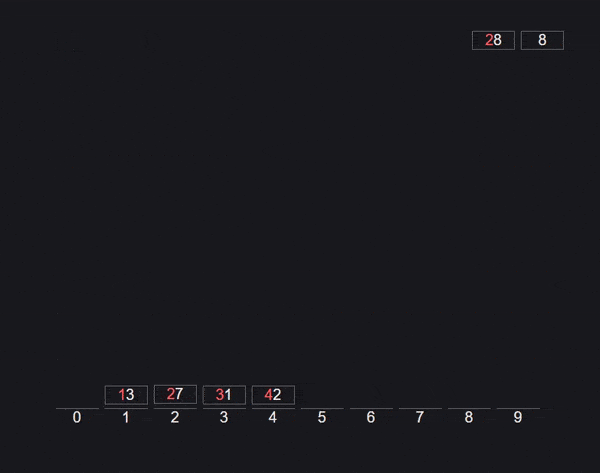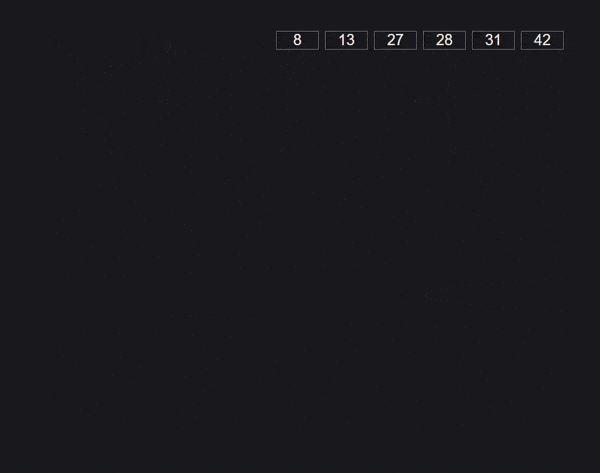
基数排序算法

基数排序也称为桶排序算法。

首先我们建立10个索引从0到9的桶。然后取每个数字的最后一个字符，并将数字推送到相应的桶中。检索新顺序并重复每个数字的倒数第二个字符。

不断重复上述过程，直到数组排序完毕。

代码实现。

// Count Digits：下面的代码计算给定元素的位数。
function countDigits(number) {
    if(number === 0) return 1;

    return Math.floor(Math.log10(Math.abs(number))) + 1;
}

// Get Digit：下面的代码从右侧给出索引i处的数字。
function getDigit(number, index) {
    const stringNumber = Math.abs(number).toString();
    const currentIndex = stringNumber.length - 1 - index;

    return stringNumber[currentIndex] ? parseInt(stringNumber[currentIndex]) : 0;
}

// MaxDigit：以下代码段查找具有最大位数的数字。
function maxDigit(array) {
    let maxNumber = 0;

    for(let i = 0; i < array.length; i++) {
        maxNumber = Math.max(maxNumber, countDigits(array[i]));
    }

    return maxNumber;
}

// 基数算法：利用上述所有片段对数组进行排序。
function radixSort(array) {
    let maxDigitCount = maxDigits(array);

    for(let i = 0; i < maxDigitCount; i++) {
        let digitBucket = Array.from({length: 10}, () => []);

        for(let j = 0; j < array.length; j++) {
            let lastDigit = getDigit(array[j], i);
            digitBucket[lastDigit].push(array[j]);
        }

        array = [].concat(...digitBucket);
    }

    return array;
}

基数排序算法的时间复杂度

因为有一个嵌套的for循环，而嵌套for循环的时间复杂度是O(n^2)。但在这种情况下，两个for循环都不会运行n次。

外循环运行k (maxDigitCount) 次，内循环运行m（数组长度）次。因此基数排序的时间复杂度是O(k x m)(其中k x m = n)：线性时间复杂度O(n)

好的，这篇文章到这里就结束了。

祝编码快乐！