TypeScript 类型编程: 从基础到编译器实战 - 哈喽比特

334次阅读 | 发布于2年以前

Typescript 的类型编程可以理解为一门有限的函数式编程语言。

本文假定读者已经使用过 typescript 并且了解基础的类型概念，不会介绍基础概念，主要专注于介绍如何进行系统化的类型编程。示例主要来源于官网、类型挑战仓库以及日常开发。

一、类型编程基础

既然称作类型编程，那自然和普通编程语言一样，用于类型变量定义语句、类型表达式、类型函数等等，本小结将详细讲述类型编程的一些基础知识。

希望通过本文能够帮助读者更好的理解 TS 的类型，让日常开发中的类型操作更加容易。

看大佬们用 ts 类型实现编译器，看起来非常其实（确实厉害=_=），不过理解这篇文章的思想后，读者们也可以实现～文章最后一个示例实现了一个简易加法表达式求值器。

1. 类型变量定义

TS 定义类型的方式有多种：

使用 type。
使用 interface。
使用 class、enum 等等，其中 class、enum 可以既为值，又为类型。

TS 提供了大量的基础类型，可以直接在定义类型变量时使用（关于基础类型的详细介绍可以查阅 TS 文档）：

基础数据类型，比如 string、number、boolean、symbol、undefined 等等。
字面量类型，比如 '123'，5 等
对象类型，比如 { a: string }
函数类型，比如 (a: string) => void
元组类型，比如 [1, 2, 3]
数组类型，比如 string[]
...

// 使用 type 定义类型变量，类型是一个字面亮类型 '123'
type TypeA = '123'

// 使用 interface 定义类型变量
interface TypeB {
  a: string
}

// 将对象类型
// {
//  b: number
//  c: TypeA
// } 
// 赋值给 TypeC
// TypeA 是上面定义的类型变量，可以直接使用
type TypeC = {
  b: number
  c: TypeA
}

// 类型变量可以直接赋值给另一个类型变量
type D = TypeB
// 将函数类型赋值给 E
type E = (a: string) => void;

基于 TS 的基础类型以及 type 等关键字，就可以定义自定义的类型变量。

2. 类型操作符

ts 中也定义了大量类型操作，例如 &（对象类型合并）、|（联合类型）等等，这些操作可以操作 TS 的类型。

2.1 & - 合并类型对象

& 合并多个类型对象的键到一个类型对象中。

type A = { a: number }
type B = { b: string }
type C = A & B;
// C 包含 A 和 B 定义的所有键
/**
* C = {
    a: number;
    b: string;
  }
*/
const c: C = {
  a: 1,
  b: '1'
}

注意使用 & 时，两个类型的键如果相同，但类型不同，会报错：

type A = { a: number }
type B = { a: string }
type C = A & B;
/**
报错：
Type 'number' is not assignable to type 'never'.(2322)
input.tsx(62, 3): The expected type comes from property 'a' which is declared here on type 'C'
(property) a: never
*/
const c: C = {
  a: 1 // error
}

2.2 | - 联合类型

|将多个类型组成联合类型：

type A = string | number;
type B = string;

此时类型 A 既可以是 string 又可以是 number，类型 B 是类型 A 的子集，所有能赋值给类型 B 的值都可以赋值给类型 A。

2.3 keyof - 获取对象类型的键

keyof 可以获取某些对象类型的键：

interface People {
  a: string;
  b: string;
}

// 返回 'a' | 'b'
type KeyofPeople = keyof People;
// type KeyofPeople = 'a' | 'b';

用这种方式可以获取某个类型的所有键。

注意 keyof 只能对类型使用，如果想要对值使用，需要先使用 typeof 获取类型。

2.4 typeof - 获取值的类型

typeof 可以获取值的类型。

// 获取对象的类型
const obj = { a: '123', b: 123 }
type Obj = typeof obj;
/**
type Obj = {
    a: string;
    b: number;
}
*/

// 获取函数的类型
function fn(a: Obj, b: number) {
  return true;
}
type Fn = typeof fn;
/**
type Fn = (a: Obj, b: number) => boolean
*/

// ...获取各种值的类型

注意对于 enum 需要先进行 typeof 操作获取类型，才能通过 keyof 等类型操作完成正确的类型计算（因为 enum 可以是类型也可以是值，如果不使用 typeof 会当值计算）：

enum E1 {
  A,
  B,
  C
}

type TE1 = keyof E1;
/**
拿到的是错误的类型
type TE1 = "toString" | "toFixed" | "toExponential" | "toPrecision" | "valueOf" | "toLocaleString"
*/

type TE2 = keyof typeof E1;
/**
拿到的是正确的类型
type TE2 = "A" | "B" | "C"
*/

2.5 [...] - 元组展开与合并

元组可以视为长度确定的数组，元组中的每一项可以是任意类型。通过 [...元组, ...元组] 语法可以合并两个元组。

结合元组展开以及 infer 类型推断，可以实现类型中的数组操作，比如 pop()，后文介绍 infer 时将详细介绍。

type TupleA = [1, 2, 3]
type TupleB = [...TupleA, 4]
/**
type TupleB = [1, 2, 3, 4]
*/
type TupleC = [0, ...TupleA]
/**
type TupleC = [0, 1, 2, 3]
*/

2.6 [in] - 遍历对象键值

在对象类型中，可以通过 [临时类型变量 in 联合类型] 语法来遍历对象的键，示例如下：

// 下述示例遍历 '1' | '2' | 3' 三个值，然后依次赋值给 K，K 作为一个临时的类型变量可以在后面直接使用 
/**
下述示例最终的计算结果是：
type MyType = {
    1: "1";
    2: "2";
    3: "3";
}
因为 K 类型变量的值在每次遍历中依次是 '1', '2', '3' 所以每次遍历时对象的键和值分别是 { '1': '2' } { '2': '2' } 和 { '3': '3' }，
最终结果是这个三个结果取 &
*/
type MyType = {
  // 注意能遍历的类型只有 string、number、symbol，也就是对象键允许的类型
  [K in '1' | '2' | '3']: K 
}

[in] 常常和 keyof 搭配使用，遍历某一个对象的键，做相应的计算后得到新的类型，如下：

type Obj = {
  a: string;
  b: number;
}
/**
遍历 Obj 的所有键，然后将所有键对应的值的类型改成 boolean | K，返回结果如下：
type MyObj = {
    a: boolean | "a";
    b: boolean | "b";
}
这样我们就实现了给 Obj 的所有值的类型加上 | boolean 的效果
*/
type MyObj = {
  [K in keyof Obj]: boolean | K
}

in 后面还可以接 as，as 后面可以接类型表达式（文档：https://www.typescriptlang.org/docs/handbook/2/mapped-types.html#key-remapping-via-as）

type Getters<Type> = {
    [Property in keyof Type as `get${Capitalize<string & Property>}`]: () => Type[Property]
};

3. 泛型 - 类型函数

TS 的泛型可以类比 Javascript 中的函数

3.1 定义泛型

使用定义泛型:

// 接口泛型
interface Obj1<T> {
  a: T
}
// 使用 type 也能定义泛型
type Type1<T> = { b: T }
// 函数泛型
type Fn1 = <T>(...args: any[]) => any;

// 泛型也可以有默认值，这样如果没有指定泛型参数，默认是 string
interface Obj1<T = string> {
  a: T
}

通过 extends 可以约束泛型：

// extends 后可以接类型表达式
type Fn2 = <T extends string | number>(...args: any[]) => any;

// 泛型可以和函数泛型结合
type Fn3<I> = <T extends string | number>(...args: T[]) => I;

在 <> 中定义的泛型变量可以视为一个局部函数变量，例如上例中的 T，可以作为类型表达式在后续所有涉及类型的地方使用。

3.2 基于泛型创建新类型 - 函数调用

通过 泛型名<类型表达式> 即可使用泛型生成新类型，如下：

type Fn3<I> = <T extends string | number>(...args: T[]) => I;

type MyFn = Fn3<boolean>;
/** 可以看到 Fn3 中的类型已经被替换成了 boolean，也就是我们指定的参数类型
type MyFn = <T extends string | number>(...args: T[]) => boolean
*/

// 使用新类型
const myfn: MyFn = (a: any) => true;

上例中，返回的 MyFn 是一个新类型，可以直接使用新类型进行类型计算，或者进行类型限定。

3.3 泛型递归调用 - 函数递归

泛型调用支持递归:

type RecursiveGenerics<T> = T extends string ? T : RecursiveGenerics<T>;

在上个例子中，我们定义了一个泛型 RecursiveGenerics<T>，当 T 是 string 的时候，RecursiveGenerics<T> 返回 T，否则返回一个递归的结果！

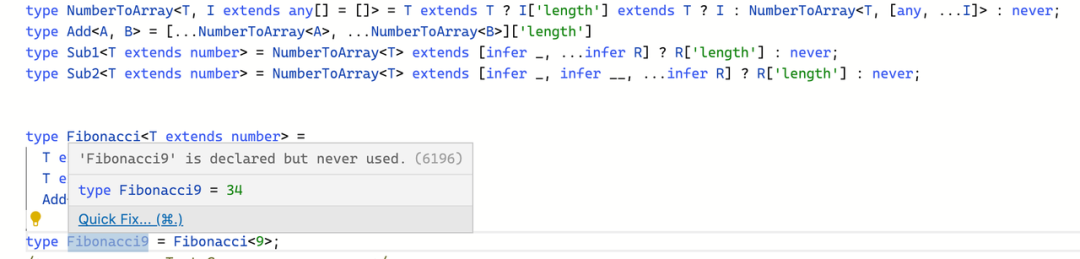
例如递归我们就可以做很多有意思的事情了，比如类型对象的深度优先遍历、实现循环等等。下面我们给斐波那契数列计算的例子：

// 辅助函数，暂时不用关心
type NumberToArray<T, I extends any[] = []> = T extends T ? I['length'] extends T ? I : NumberToArray<T, [any, ...I]> : never;
type Add<A, B> = [...NumberToArray<A>, ...NumberToArray<B>]['length']
type Sub1<T extends number> = NumberToArray<T> extends [infer _, ...infer R] ? R['length'] : never;
type Sub2<T extends number> = NumberToArray<T> extends [infer _, infer __, ...infer R] ? R['length'] : never;

// 计算斐波那契数列
type Fibonacci<T extends number> = 
  T extends 1 ? 1 :
  T extends 2 ? 1 :
  Add<Fibonacci<Sub1<T>>, Fibonacci<Sub2<T>>>;

  type Fibonacci9 = Fibonacci<9>;
  /** 得到结果
  type Fibonacci9 = 34
  */

上述示例中我们成功使用类型完成了斐波那契数列的计算：

重点是下面几句，根据条件类型判断递归条件，然后调用递归。

下述示例使用的条件类型判断边界，下一小节会介绍条件类型

// 辅助函数，暂时不用关心
type NumberToArray<T, I extends any[] = []> = T extends T ? I['length'] extends T ? I : NumberToArray<T, [any, ...I]> : never;
type Add<A, B> = [...NumberToArray<A>, ...NumberToArray<B>]['length']
type Sub1<T extends number> = NumberToArray<T> extends [infer _, ...infer R] ? R['length'] : never;
type Sub2<T extends number> = NumberToArray<T> extends [infer _, infer __, ...infer R] ? R['length'] : never;

// 计算斐波那契数列
type Fibonacci<T extends number> = 
  T extends 1 ? 1 :
  T extends 2 ? 1 :
  Add<Fibonacci<Sub1<T>>, Fibonacci<Sub2<T>>>;

  type Fibonacci9 = Fibonacci<9>;
  /** 得到结果
  type Fibonacci9 = 34
  */

4. 条件类型 - if else

4.1 条件类型

使用 extends 三元表达式能够进行条件的判断，并返回一个新类型，语法如下：

类型表达式1 extends 类型表达式2 ？ 类型表达式 : 类型表达式

示例:

type C = 'a' extends 'a' | 'b' ? true : false
/**
type C = true
*/

这里有几个注意点：

三元表达式的所有位置都可以使用类型表达式
返回值是一个类型表达式

4.2 Infer 推断类型

可以使用 infer 关键字推断条件类型中的某一个条件类型，然后将该类型赋值给一个临时的类型变量。类型推断可以用于 extends 后任何可以使用类型表达式的位置，示例：

type Flatten<Type> = Type extends Array<infer Item> ? Item : Type;

上述示例中，当 type 满足 Array模式时，将会自动推断出 T 的类型，并赋值给 Item。例如：

type T = Flatten<string[]>; 
/* T = string, 因为推断出 string[] = Array<string>，所以 Item = string，类型返回 Item */

注意：infer 只能在条件类型里面使用。

通过 infer 关键字，可以实现很多的内置类型的操作，比如 Parameters、ReturnType 等，实现方式如下：

// 自动推断参数 P 的类型，如果是则泛型返回值是 P
type MyParameters<T> = T extends (...args: infer P) => any ? P : never;
/**
推断参数的类型成功
type Params = [a: string, b: number]
*/
type Params = MyParameters<(a: string, b: number) => void>;

// 同样的方式，我们可以推断 ReturnType
type MyReturnType<T> = T extends (...args: any[]) => infer R ? R : never;
/**
团队返回值的类型成功
type Ret = void
*/
type Ret = MyReturnType<(a: string, b: number) => void>;

infer 的能力很强大，可以推断任何类型表达式，例如 infer 还可以和元组或者模版字符串结合，两个示例如下：

// 计算元组中的第一个元素
type Head<T extends any[]> = T extends [infer F, ...infer R] ? F : never;

// 解析 `1 + 2 + 3` 形式的字符串，并返回 AST
type Parse<T extends string> = T extends `${infer ExpressionA} + ${infer ExpressionB}` ? {
  type: 'operator',
  left: Parse<ExpressionA>,
  right: Parse<ExpressionB>
}: {
  type: 'expression',
  value: T
};

上述示例中，Head<T> 的计算使用了上文提到的元组展开与合并知识点，然后结合本小节的infer，就可以推断出数组的第一个元素。Parse<T> 中使用了条件类型、递归知识点，再结合本小节的infer，就可以实现一个简单的加法表达式解析器。主要实现是：T extends ${infer ExpressionA} + ${infer ExpressionB}，如果字符串满足 A + B 的模式，即可通过 infer 推断出 A 和 B 的字符串。

4.3 条件联合类型

如果条件类型的参数是一个联合类型，则条件类型的计算结果相当于，如下：

// 这里等价于 (string exetends any ? string[] : never) | (number exetends any ? number[] : never)
type ToArray<Type> = Type extends any ? Type[] : never; 
// 计算结果是 string[] | number[]
type StrArrOrNumArr = ToArray<string | number>;

利用这个特性我们可以实现一些有意思的功能，比如 Excludes：

type Exclude<T, I> = T extends I ? never : T;
type T0 = Exclude<"a" | "b" | "c", "a">;
/**
type T0 = "b" | "c"
*/

原理是联合类型的每一个类型都会计算一次 extends，然后将最终的结果做联合，never 在联合过程中会去除。

二、类型表达式

类型表达式仅是是本文给出的概念，便于读者进一步理解类型编程。目前官网文档中没有体现类似的概念，如果有不正确的地方，欢迎读者指正。笔者认为类型表达式是本文中最核心的一个概念，理解了此概念后，类型计算的问题都将迎刃而解。

值是一个类型的表达式就是类型表达式，通常：

定义的类型变量是一个类型表达式
类型操作符的操作结果是一个类型表达式，比如 A | B 是一个类型表达式，会返回一个新的类型
泛型调用结果是一个类型表达式，比如 A<string> 是一个类型表达式
条件类型的结果是一个类型表达式，比如 A extend string ? true : false 是一个类型表达式，返回值是类型 true 或者 false
...

在需要使用类型的地方，我们就可以使用类型表达式：

类型变量定义：比如 type A = B，B 就可以是一个类型表达式，比如 type A = string | Record<string, string>
泛型调用：比如 A<B>，B 就可以是一个类型表示，比如 A<string | number | boolean>
条件类型：比如 A extend B ? C : D，A、B、C、D 均可以是类型表达式
...

总而言之，所有使用类型的地方，都可以使用类型表达式，比如类型变量赋值、条件类型、函数参数/返回值类型等等位置。利用 TS 类型表达式的概念，我们就可以进行强大的类型编程能力。

下面通过几个示例来帮助理解类型表达式的概念。

首先可以拿上面的斐波那契数列计算作为第一个示例：

type Fibonacci9 = Fibonacci<9>;
// Fibonacci<9> 是一个类型表达式，那么可以将其作为 Fibonacci 的输入，如下：
type Fibonacci99 = Fibonacci<Fibonacci<9>>; // 等价于 type Fibonacci99 = Fibonacci<Fibonacci9>

Fibonacci<9> 是一个类型表达式，我们可以将这个类型表达式作为泛型的输入，所以 Fibonacci<Fibonacci<9>> 也是合法的！由此我们可以拓展，所有合法的类型表达式都可以在这里使用。

另一个示例是条件类型，我们前面介绍了条件类型的语法是：类型表达式1 extends 类型表达式2 ？类型表达式3 : 类型表达式。

type MyType = Fibonacci<9> extends Fibonacci<9> ? Fibonacci<10> : Fibonacci<8>;

示例中的四个位置都可以使用类型表达式。

基于类型表达式的概念，我们可以通过堆砌小的类型表达式，完成复杂的类型编程操作！

三、常用知识点总结

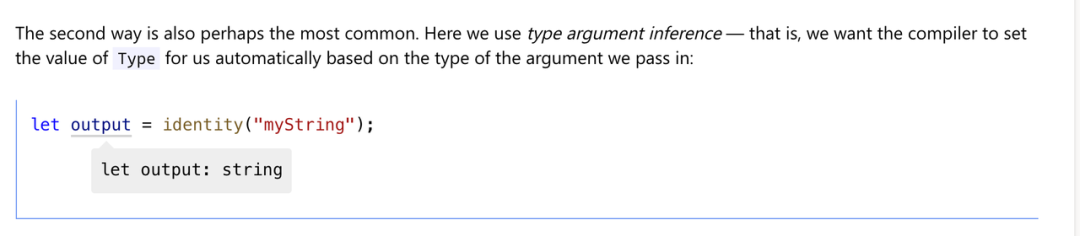
1. 函数参数类型自动推导

通过泛型 + 函数参数，可以定义一个类型变量，并且由函数参数自动推导类型变量的值：

function identity<Type>(arg: Type): Type {
  return arg;
}

通过传入一个 string 类型的参数，可以推导出 Type=string ，同时这个类型参数可以在用于组合其他类型！

这个特性非常有用，有时候我们需要推断出函数参数的类型，并将其保存到一个临时类型变量中时，这个特性就可以很方便的实现，下面实战的链式调用中用到了这个特性。

2. 动态扩展类型变量

如下，T 中可保存上一次调用 option 后的值，然后通过类型递归，扩展 T 的类型，当最后调用 get() 时，拿到的就是扩展后的 T 的类型：

type Chainable<T = {}> = {
  option<K extends string, V extends any>(key: K, value: V): Chainable<T & { [key in K]: V }>
  get(): T
}

上述示例中，我们使用了默认泛型 + 递归两个特性，利用递归保存上下文，我们就可以实现对已有类型变量的扩展。利用这个特性我们可以保存链式调用中的上下文。

3. 动态更改对象类型的 key

通过 key in keyof T as xxx形式可以重写 key。可以通过这种形式来实现动态更改对象类型的 key，比如实现 OptionalKeys 或者 RequiresKeys 或者 ReadonlyKeys。

type IsOptional<T, K extends keyof T> = Partial<Pick<T, K>> extends Pick<T, K> ? true : false;

type OptionalKeys<T> = keyof {
  [K in keyof T as IsOptional<T, K> extends true ? K : never]: T[K];
};

type RequiredKeys<T> = {
  [K in keyof T]: IsOptional<T, K> extends true ? never : T[K]
}

这里注意 as 后面可以接一个类型表达式，我们可以通过临时变量 K 以及辅助的类型表达式，实现对键的复杂的操作，比如增加、删除特定的键，将特定的键标记为可选，将特定的键标记为 readonly 等等。

上述根据条件将 K 的类型重写为 never 可以去掉该 key，但是注意将值的返回类型设置成 never 是无法更改 key 的数量的，如下：

type RequiredKeys<T> = {
  [K in keyof T]: IsOptional<T, K> extends true ? never : T[K]
}

返回的 never 值将会变为 undefined。

四、类型编程实战

4.1 常用的 ts 内置类型

参考：https://www.typescriptlang.org/docs/handbook/utility-types.html#excludetype-excludedunion

常用的有：

Partial
Omit
Record
Pick
ReturnType
Parameters

我们上面的示例中自己实现了 ReturnType、Parameters，其他的内置类型的实现也类似。基于上述的基础知识，我们都可以自行实现。

4.2 将某一个对象中的部分参数标记为可选

使用 Partial 只能将所有参数标记为可选，如何只标记一部分参数呢？可以如下实现:

type Include<T, I> = T extends I ? T : never;

type MyPartial<T, I> = {
  [for K in Exclude<keyof T, I>]: T[K] 
} & {
  [for K in Include<keyof T, I>]?: T[K] 
}

上述示例将 T 的键分成两部分，如果属于 I 则标记成可选，如果不是则为必须的。

4.3 给链式调用添加类型

题目：https://github.com/type-challenges/type-challenges/blob/master/questions/12-medium-chainable-options/README.md

type Chainable<T = {}> = {
  option<K extends string, V extends any>(key: K, value: V): Chainable<T & { [key in K]: V }>
  get(): T
}

利用了 TS 函数的范性自动推断能力以及递归函数存储能力。

4.4 柯里化函数类型

type Head<T extends any[]> = T extends [infer F, ...infer R] ? F : never;
type Rest<T extends any[]> = T extends [infer F, ...infer R] ? R : never;

declare function Currying<T extends any[], P extends boolean>(fn: (...args: T) => P): CurryingRet<T, P>;
type CurryingRet<T extends any[], P> = T['length'] extends 0 ? P : (arg0: Head<T>) => CurryingRet<Rest<T>, P> ;

这里实现的是简化版本，更详细的实现可以参考文章：https://medium.com/free-code-camp/typescript-curry-ramda-types-f747e99744ab。

Head 和 Rest 的计算上文有详细介绍，这里我们主要利用了递归 + 函数泛型自动推断的特性。

4.5 简易加法表达式求值器

实现：Calculator<'1 + 2 + 3'> 输出 6。

先上效果：

实现思路：

实现 Parse，将计算表达式解析成 AST
实现 AST 遍历器
实现求值器，输出最终结果

/* _____________ Your Code Here _____________ */
type ASTExpressionNode = {
  type: 'operator' | 'expression';
  left?: ASTExpressionNode;
  right?: ASTExpressionNode;
  value?: keyof NumberMap;
}

type Parse<T> = T extends `${infer ExpressionA} + ${infer ExpressionB}` ? {
  type: 'operator',
  left: Parse<ExpressionA>,
  right: Parse<ExpressionB>
}: {
  type: 'expression',
  value: T extends keyof NumberMap ? T : never
};

type NumberToArray<T, I extends any[] = []> = I['length'] extends T ? I : NumberToArray<T, [any, ...I]>;
type Add<A, B> = [...NumberToArray<A>, ...NumberToArray<B>]['length'];

type GetValue<T extends ASTExpressionNode> = T['value'] extends string ? T['value'] : never;
type GetLeft<T extends ASTExpressionNode> = T['left'] extends ASTExpressionNode ? T['left'] : never;
type GetRight<T extends ASTExpressionNode> = T['right'] extends ASTExpressionNode ? T['right'] : never;

type NumberMap = {
  '0': 0,
  '1': 1,
  '2': 2,
  '3': 3,
  '4': 4,
};

type Evaluate<T extends ASTExpressionNode> = T['type'] extends 'expression' ? NumberMap[`${GetValue<T>}`] : Add<Evaluate<GetLeft<T>>, Evaluate<GetRight<T>>>;

type Calculator<T extends string> = Evaluate<Parse<T>>;

type test1 = Parse<'1 + 2'>;
/** 返回
type test1 = {
    type: 'operator';
    left: {
        type: 'expression';
        value: "1";
    };
    right: {
        type: 'expression';
        value: "2";
    };
}
*/
type test2 = Calculator<'1 + 2 + 3'>
/** 返回
type test2 = 6
*/

这里我们利用了上面提到的几乎所有知识点：

递归：表达式的解析和求值都使用了递归的能力
条件类型：实现递归的边界判断
类型推断：通过类型推断实现 Head、Tail 等能力
...

感兴趣的同学还可以自行实现减法、乘法、除法、取模等操作~

五、常用 TS 类型工具库

5.1 ts-toolbelt

封装常用的 TS 类型操作。

地址: https://github.com/millsp/ts-toolbelt。

3.2 typetype

用于自动生成 TS 的类型。

地址: https://github.com/mistlog/typetype。