字节一面:非递归手写快速排序
今天给大家讲解一道非常有趣的算法面试题,以非递归的形式来写快速排序。
其实这也可以衍生出更多同类问题,非递归二叉树的前序、中序、后序遍历等等,这些问题的背后的思想是一致的,那就是用栈来手动模拟递归调用。
道理很简单有没有,一句话就能说清楚,但问题是你真的理解了吗?该怎样用栈来手动模拟递归调用呢?你的大脑在面对这个问题时有一个清晰的思路吗?
别着急,我们先从最简单的快排开始。
快排,quick sort
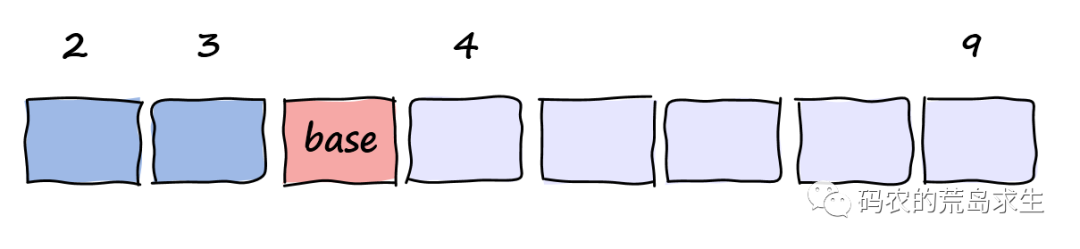
快速排序想必大家都知道,我们以数组中的某个数字为基准,通常是数组的第一个或者最后一个(当然也可以是其它选择方式),这里假设以数组的最后一个元素为基准:
然后将数组中小于该基准的数字放在左边、将大于该数字的放在右边:
经过这一次处理后base就被放到了最终的位置上并得到了两个子数组:base左边的数组和base右边的数组,以同样的方式处理这两个子数组即可。
用代码表示就是这样:
void quick_sort(vector<int>&arr, int b, int e) {
if (b >= e) return;
int i = b - 1;
for (int k = b; k < e; k++)
if (arr[k] < arr[e])
swap(&arr[++i], &arr[k]);
swap(&arr[++i], &arr[e]);
quick_sort(arr, b, i - 1);
quick_sort(arr, i + 1, e);
}其中参数中的b和e表示begin和end,也就是范围。
可以看到,最终使用递归的方式编写的代码非常简洁,也很容易理解,递归是计算机科学中一个极其重要的概念,递归对于理解编译原理、编程语言、分而治之算法思想、排序以及动态规划等等有重要的意义,我在星球中以最通俗易懂的方式讲解了一期专栏《程序员应如何理解递归》,总共八篇,一万余字,岛友们可以去看看。
递归版本很简单有没有,如果让你用非递归的方式来实现呢?
非递归手写快速排序
想一想这个问题!如果你真正理解递归的话那么就应该能写出来。
我们再来看看这个递归写法。
首先会得到一个问题quick_sort(arr, b, e),我们利用base进行一次划分后得到两个子问题:
- quick_sort(arr, b, i - 1)
- quick_sort(arr, i + 1, e)
在递归版本中这两个子问题的状态(所谓的状态就是要解决哪个子问题,这里用参数中的begin和end来界定)是随着函数的调用自动保存在栈帧中的,而我们需要用栈这种数据结构来模拟这个过程。
接下来,我们用变量task来表示要处理的子问题,也就是说入栈出栈的都是task,task可以这样定义:
pair<int, int>
表示要对哪一段数组进行排序,因此使用了pair<int, int>来记录这段数组的开始和结尾。
由于需要使用栈来追踪问题的解决顺序,因此我们最终这样定义栈:
stack<pair<int, int>> tasks;
一切准备就绪,是时候创建些任务了,任务的起源是什么呢?很简单,就是数组本身:
int size = arr.size();
tasks.push(pair<int, int>(0, size - 1));接下来就是最重要的部分了:
while (!tasks.empty()) {
// 取出栈顶元素
// 处理
// 是否有新的子任务需要push到栈中
}整体的框架就是这样,接下来的三个问题就是:
- 取出栈顶元素
- 处理
- 是否有新的子任务需要push到栈中,如果有则push到栈中
第一个问题很简单,没什么可说的;第二个问题是说我们该怎样处理一个子问题,其实也很简单,就是用base将数组划分为两个子数组。
第三个问题是重点,我们该怎么知道接下来是否有新的子任务需要push到栈中呢?
想一想这个问题。。。
如果用base对数组进行划分后发现数组已经是有序的那么就没有必要创建子任务了,因为当前的数组已经有序了嘛!否则我们就需要创建子任务。
因此我们必须知道对数组进行划分后数组是不是已经排好序。
基于上述讨论,我们可以这样实现划分函数partition:
int partition(vector<int>&arr, int b, int e, bool* sorted) {
if (b > e || b == e) return -1;
int i = b - 1;
for (int j = b; j < e; j++) {
if (arr[j] < arr[e]) {
*sorted = false;
swap(arr[++i],arr[j]);
}
}
swap(arr[++i], arr[e]);
return i;
}这其实和开始递归版本中quick_sort函数里的划分部分代码没什么区别,变化的部分仅在于我们将一次划分后base所在的下标以及判断一次划分后数组是否有序记录在参数sorted中。
一次划分后如果sorted的值为true也就是数组已经有序那么我们无需再创建新的子问题,一次划分后我们得到两个新的更小的子问题,即:
bool sorted = true;
int p = partition(arr, top.first, top.second, &sorted);
if (sorted) {
continue;
} else {
tasks.push(pair<int,int>(p + 1, top.second));
tasks.push(pair<int,int>(top.first, p - 1));
}所有问题分析完毕,完整的代码为:
void quick_sort(vector<int>&arr) {
int size = arr.size();
if (size == 0 || size == 1) return ;
stack<pair<int,int>> tasks;
tasks.push(pair<int,int>(0, size - 1));
int b = 0;
while(!tasks.empty()) {
auto top = tasks.top();
tasks.pop();
bool sorted = true;
int p = partition(arr, top.first, top.second, &sorted);
if (sorted) {
continue;
} else {
tasks.push(pair<int,int>(p + 1, top.second));
tasks.push(pair<int,int>(top.first, p - 1));
}
}
}运行一下,it works like magic,有没有!
这段代码是怎样运行的?
No,其实一点都不magic,接下来我们仔细看看这段代码是怎么运行的。
假设当前栈顶元素为(2,9),我们获取栈顶元素,并将其从中pop掉:
此时我们要对数组下标2到9的元素进行排序,把末尾的base作为基准进行划分:
假设划分后base放到了下标为5的位置,这样我们得到了两个子问题(2,3)以及(4,9):
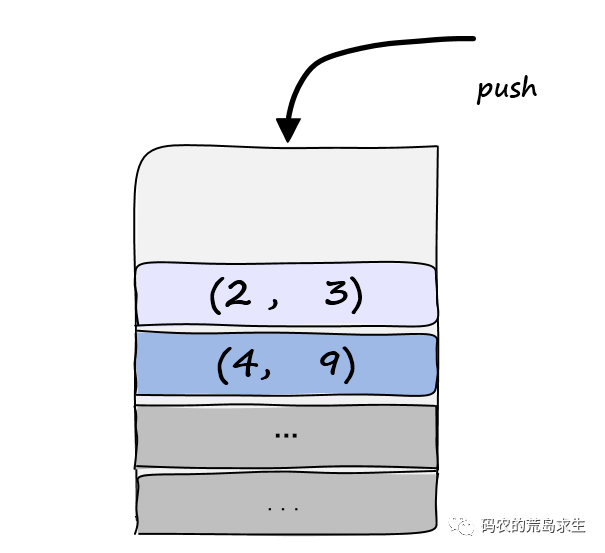
由于经过base的划分后我们判断出该数组不是有序的(partition函数中sorted参数的作用),因此我们需要将两个子问题(2,3)以及(4,9)放到栈中:
就这样,我们解决了子任务(2,9),并得到了两个更小的子问题(2,3)以及(4,9),接着while循环继续从栈中弹出任务并重复上述过程,当栈为空时我们一定能确信数据已经有序了。
这个过程“完全”模拟了上述递归函数的调用,这里之所以加了引号,是因为我们的迭代快排版本进行了一点点小小的优化,这个优化是什么呢?
尾递归
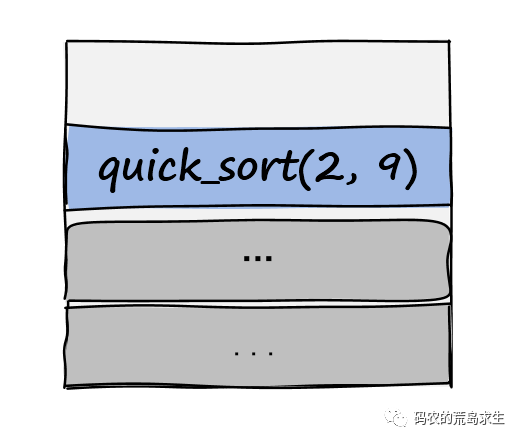
依然假设递归调用到函数quick_sort(2,9),此时的函数栈帧为:
基于base划分后依然得到:
根据递归版本的quick_sort实现接着我们需要调用quick_sort(2,3),此时的栈帧为:
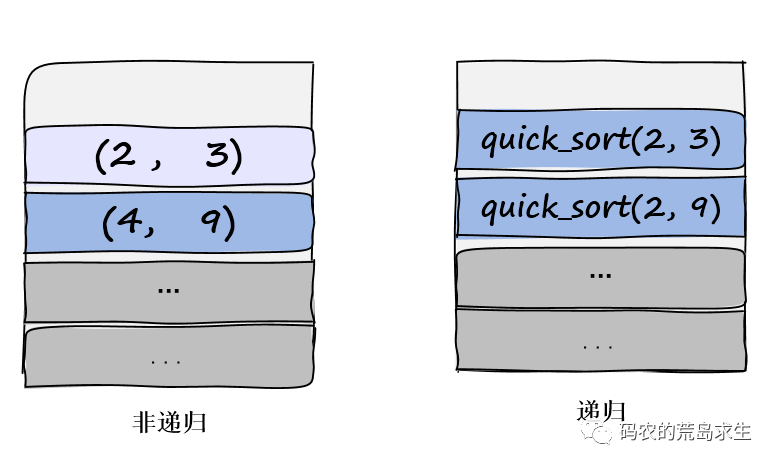
看到非递归版本与递归版本的不同了吧:
在非递归版本下,对处理子任务(2,9)时会将该任务从栈中pop出来,而递归版本则不会pop出quick_sort(2,9)的栈帧,函数quick_sort(2,3)执行完后还会再次回到函数quick_sort(2,9),然后接着调用函数quick_sort(4,9)。
而之所以非递归实现可以提前将子任务(2,9)从栈中弹出是因为递归版本下所有递归调用都位于函数的末尾,这就是所谓的“尾递归”。
尾递归是一种比较常见的现象,二叉树的前序遍历递归实现也是这样:
void tree_travel(Tree* t) {
if (t) {
print(t->value);
tree_travel(t->left);
tree_travel(t->right);
}
}你可以使用和本文一样的套路将上述递归代码转为非递归代码,但是如果是二叉树的中序遍历或者后序遍历呢?
void tree_travel(Tree* t) {
if (t) {
tree_travel(t->left);
print(t->value);
tree_travel(t->right);
}
}此时,本文中讲解的套路就失效了,因此我们需要一种更加通用的方法将此类非尾递归代码转为递归代码,这种通用的方法是什么呢?
我将该方法总结在了星球中最新一期的专栏《如何将递归转为非递归代码?》,总共五篇,岛友们可以去看看。
希望本篇对大家理解递归、栈、快排有所帮助。