一、前言

首先，为什么我会学习数据结构与算法呢，其实主要是有两方面

第一，是我在今年的flag里明确说到我会学这个东西
第二，学了这些，对自己以后在工作或者面试也会带来许多好处

然后，本文是最近学习的一个总结文章，文中的算法题，大部分都是leetcode中的，如不太理解题意，可直接去leetcode中找到对应的题。

二、基本概念

常常听到算法的时候，就会有人说到 时间复杂度， 空间复杂度。那么这俩玩意是啥呢，下面我们就来一一解释

1 . 时间复杂度

其实就是一个函数，用大 O 表示，比如 O(1)、 O(n)...

它的作用就是用来定义描述算法的运行时间

O(1)

    let i = 0
    i += 1

O(n)： 如果是 O(1) + O(n) 则还是 O(n)

    for (let i = 0; i < n; i += 1) {
      console.log(i)
    }

O(n^2)： O(n) * O(n), 也就是双层循环，自此类推：O(n^3)...

    for (let i = 0; i < n; i += 1) {
      for (let j = 0; j < n; j += 1) {
        console.log(i, j)
      }
    }

O(logn)： 就是求 log 以 2 为底的多少次方等于 n

    // 这个例子就是求2的多少次方会大于i，然后就会结束循环。 这就是一个典型的 O(logn)
    let i = 1
    while (i < n) {
      console.log(i)
      i *= 2
    }

2 . 空间复杂度

和时间复杂度一样，空间复杂度也是用大 O 表示，比如 O(1)、 O(n)...

它用来定义描述算法运行过程中临时占用的存储空间大小

占用越少代码写的就越好

O(1)： 单个变量，所以占用永远是 O(1)

    let i = 0
    i += 1

O(n)： 声明一个数组，添加 n 个值，相当于占用了 n 个空间单元

    const arr = []
    for (let i = 0; i < n; i += 1) {
      arr.push(i)
    }

O(n^2)： 类似一个矩阵的概念，就是二维数组的意思

    const arr = []
    for (let i = 0; i < n; i += 1) {
      arr.push([])
      for (let j = 0; j < n; j += 1) {
        arr[i].push(j)
      }
    }

三、数据结构

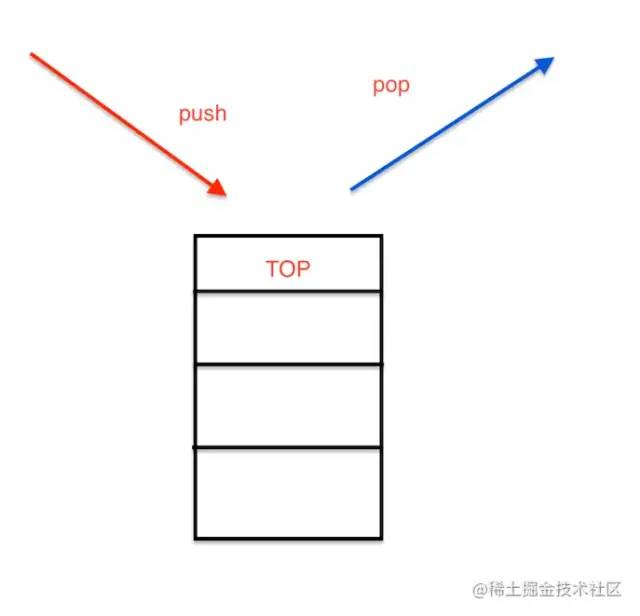
1 . 栈

一个后进先出的数据结构

按照常识理解就是有序的挤公交，最后上车的人会在门口，然后门口的人会最先下车

js中没有栈的数据类型，但我们可以通过Array来模拟一个

const stack = [];

stack.push(1); // 入栈
stack.push(2); // 入栈

const item1 = stack.pop();  //出栈的元素

1）十进制转二进制

// 时间复杂度 O(n) n为二进制的长度
// 空间复杂度 O(n) n为二进制的长度
const dec2bin = (dec) => {
  // 创建一个字符串
  let res = "";

  // 创建一个栈
  let stack = []

  // 遍历数字 如果大于0 就可以继续转换2进制
  while (dec > 0) {
    // 将数字的余数入栈
    stack.push(dec % 2);

    // 除以2
    dec = dec >> 1;
  }

  // 取出栈中的数字
  while (stack.length) {
    res += stack.pop();
  }

  // 返回这个字符串
  return res;
};

2）判断字符串的有效括号

// 时间复杂度O(n) n为s的length
// 空间复杂度O(n)
const isValid = (s) => {

  // 如果长度不等于2的倍数肯定不是一个有效的括号
  if (s.length % 2 === 1) return false;

  // 创建一个栈
  let stack = [];

  // 遍历字符串
  for (let i = 0; i < s.length; i++) {

    const c = s[i];

    // 如果是左括号就入栈
    if (c === '(' || c === "{" || c === "[") {
      stack.push(c);
    } else {

      // 如果不是左括号 且栈为空 肯定不是一个有效的括号 返回false
      if (!stack.length) return false

      // 拿到最后一个左括号
      const top = stack[stack.length - 1];

      // 如果是右括号和左括号能匹配就出栈
      if ((top === "(" && c === ")") || (top === "{" && c === "}") || (top === "[" && c === "]")) {
        stack.pop();
      } else {

        // 否则就不是一个有效的括号
        return false
      }
    }

  }
  return stack.length === 0;
};

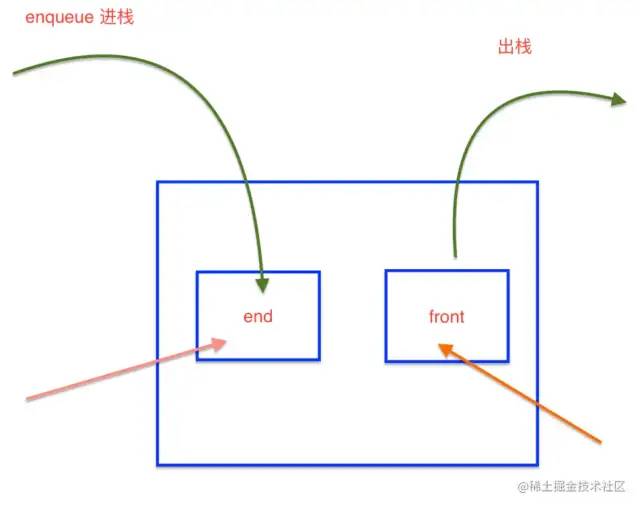
2 . 队列

和栈相反 先进先出的一个数据结构

按照常识理解就是银行排号办理业务, 先去领号排队的人, 先办理业务

同样 js中没有栈的数据类型，但我们可以通过 Array来模拟一个

const queue = [];

// 入队
queue.push(1);
queue.push(2);

// 出队
const first = queue.shift();
const end = queue.shift();

1）最近的请求次数

var RecentCounter = function () {
  // 初始化队列
  this.q = [];
};

// 输入 inputs = [[],[1],[100],[3001],[3002]] 请求间隔为 3000ms
// 输出 outputs = [null,1,2,3,3]   

// 时间复杂度 O(n) n为剔出老请求的长度
// 空间复杂度 O(n) n为最近请求的次数
RecentCounter.prototype.ping = function (t) {
  // 如果传入的时间小于等于最近请求的时间，则直接返回0
  if (!t) return null

  // 将传入的时间放入队列
  this.q.push(t);

  // 如果队头小于 t - 3000 则剔除队头
  while (this.q[0] < t - 3000) {
    this.q.shift();
  }

  // 返回最近请求的次数
  return this.q.length;
};

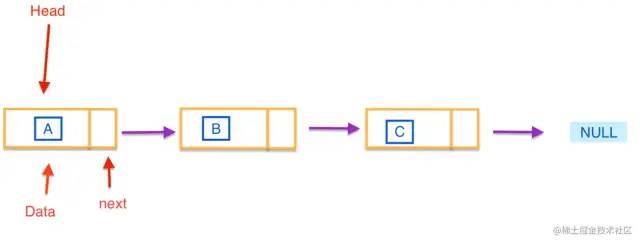
3 . 链表

多个元素组成的列表，元素存储不连续，通过 next 指针来链接, 最底层为 null

就类似于 父辈链接关系 吧，比如：你爷爷的儿子是你爸爸，你爸爸的儿子是你，而你假如目前还没有结婚生子，那你就暂时木有儿子

js中类似于链表的典型就是原型链, 但是js中没有链表这种数据结构，我们可以通过一个object来模拟链表

const a = {
  val: "a"
}

const b = {
  val: "b"
}

const c = {
  val: "c"
}

const d = {
  val: "d"
}

a.next = b;
b.next = c;
c.next = d;

// const linkList = {
//    val: "a",
//    next: {
//        val: "b",
//        next: {
//            val: "c",
//            next: {
//                val: "d",
//                next: null
//            }
//        }
//    }
// }

// 遍历链表
let p = a;
while (p) {
  console.log(p.val);
  p = p.next;
}

// 插入
const e = { val: 'e' };
c.next = e;
e.next = d;


// 删除
c.next = d;

1）手写instanceOf

const myInstanceOf = (A, B) => {
  // 声明一个指针
  let p = A;

  // 遍历这个链表
  while (p) {
    if (p === B.prototype) return true;
    p = p.__proto__;
  }

  return false
}

myInstanceOf([], Object)

2）删除链表中的节点

// 时间复杂和空间复杂度都是 O(1)
const deleteNode = (node) => {
  // 把当前链表的指针指向下下个链表的值就可以了
  node.val = node.next.val;
  node.next = node.next.next
}

3）删除排序链表中的重复元素

// 1 -> 1 -> 2 -> 3 -> 3 
// 1 -> 2 -> 3 -> null

// 时间复杂度 O(n) n为链表的长度
// 空间复杂度 O(1)
const deleteDuplicates = (head) => {

  // 创建一个指针
  let p = head;

  // 遍历链表
  while (p && p.next) {

    // 如果当前节点的值等于下一个节点的值
    if (p.val === p.next.val) {

      // 删除下一个节点
      p.next = p.next.next
    } else {

      // 否则继续遍历
      p = p.next
    }
  }

  //  最后返回原来链表
  return head
}

4）反转链表

// 1 -> 2 -> 3 -> 4 -> 5 -> null
// 5 -> 4 -> 3 -> 2 -> 1 -> null

// 时间复杂度 O(n) n为链表的长度
// 空间复杂度 O(1)
var reverseList = function (head) {

  // 创建一个指针
  let p1 = head;

  // 创建一个新指针
  let p2 = null;

  // 遍历链表
  while (p1) {

    // 创建一个临时变量
    const tmp = p1.next;

    // 将当前节点的下一个节点指向新链表
    p1.next = p2;

    // 将新链表指向当前节点
    p2 = p1;

    // 将当前节点指向临时变量
    p1 = tmp;
  }

  // 最后返回新的这个链表
  return p2;
}

reverseList(list

4 . 集合

一种无序且唯一的数据结构

ES6中有集合 Set类型

const arr = [1, 1, 1, 2, 2, 3];

// 去重
const arr2 = [...new Set(arr)];

// 判断元素是否在集合中
const set = new Set(arr);
set.has(2) // true

//  交集
const set2 = new Set([1, 2]);
const set3 = new Set([...set].filter(item => set.has(item)));

1）去重

具体代码在上面介绍中有写过，就不再重写了

2）两个数组的交集

// 时间复杂度 O(n^2) n为数组长度
// 空间复杂度 O(n)  n为去重后的数组长度
const intersection = (nums1, nums2) => {

  // 通过数组的filter选出交集
  // 然后通过 Set集合 去重 并生成数组
  return [...new Set(nums1.filter(item => nums2.includes(item)))];
}

5 . 字典

与集合类似，一个存储唯一值的结构,以键值对的形式存储

js中有字典数据结构就是 Map 类型

1）两数之和

// nums = [2, 7, 11, 15] target = 9

// 时间复杂度O(n) n为nums的length
// 空间复杂度O(n)
var twoSum = function (nums, target) {

  // 建立一个字典数据结构来保存需要的值
  const map = new Map();
  for (let i = 0; i < nums.length; i++) {

    // 获取当前的值，和需要的值
    const n = nums[i];
    const n2 = target - n;

    // 如字典中有需要的值，就匹配成功
    if (map.has(n2)) {
      return [map.get(n2), i];
    } else {

    // 如没有，则把需要的值添加到字典中
      map.set(n, i);
    }
  }
};

2）两个数组的交集

// nums1 = [1,2,2,1], nums2 = [2,2]
// 输出：[2]

// 时间复杂度 O(m + n) m为nums1长度 n为nums2长度
// 空间复杂度 O(m) m为交集的数组长度
const intersection = (nums1, nums2) => {
  // 创建一个字典
  const map = new Map();

  // 将数组1中的数字放入字典
  nums1.forEach(n => map.set(n, true));

  // 创建一个新数组
  const res = [];

  // 将数组2遍历 并判断是否在字典中
  nums2.forEach(n => {
    if (map.has(n)) {
      res.push(n);

      // 如果在字典中，则删除该数字
      map.delete(n);
    }
  })

  return res;
};

3）字符的有效的括号

// 用字典优化

// 时间复杂度 O(n) n为s的字符长度
// 空间复杂度 O(n) 
const isValid = (s) => {

  // 如果长度不等于2的倍数肯定不是一个有效的括号
  if (s.length % 2 !== 0) return false

  // 创建一个字典
  const map = new Map();
  map.set('(', ')');
  map.set('{', '}');
  map.set('[', ']');

  // 创建一个栈
  const stack = [];

  // 遍历字符串
  for (let i = 0; i < s.length; i++) {

    // 取出字符
    const c = s[i];

    // 如果是左括号就入栈
    if (map.has(c)) {
      stack.push(c)
    } else {

      // 取出栈顶
      const t = stack[stack.length - 1];

      // 如果字典中有这个值 就出栈
      if (map.get(t) === c) {
        stack.pop();
      } else {

        // 否则就不是一个有效的括号
        return false
      }

    }

  }

  return stack.length === 0;
};

4）最小覆盖字串

// 输入：s = "ADOBECODEBANC", t = "ABC"
// 输出："BANC"


// 时间复杂度 O(m + n) m是t的长度 n是s的长度
// 空间复杂度 O(k) k是字符串中不重复字符的个数
var minWindow = function (s, t) {
  // 定义双指针维护一个滑动窗口
  let l = 0;
  let r = 0;

  // 建立一个字典
  const need = new Map();

  //  遍历t
  for (const c of t) {
    need.set(c, need.has(c) ? need.get(c) + 1 : 1)
  }

  let needType = need.size

  // 记录最小子串
  let res = ""

  // 移动右指针
  while (r < s.length) {

    // 获取当前字符
    const c = s[r];

    // 如果字典里有这个字符
    if (need.has(c)) {

      // 减少字典里面的次数
      need.set(c, need.get(c) - 1);

      // 减少需要的值
      if (need.get(c) === 0) needType -= 1;
    }

    // 如果字典中所有的值都为0了 就说明找到了一个最小子串
    while (needType === 0) {

      // 取出当前符合要求的子串
      const newRes = s.substring(l, r + 1)

      // 如果当前子串是小于上次的子串就进行覆盖
      if (!res || newRes.length < res.length) res = newRes;

      // 获取左指针的字符
      const c2 = s[l];

      // 如果字典里有这个字符
      if (need.has(c2)) {
        // 增加字典里面的次数
        need.set(c2, need.get(c2) + 1);

        // 增加需要的值
        if (need.get(c2) === 1) needType += 1;
      }
      l += 1;
    }
    r += 1;
  }
  return res
};

6 . 树

一种分层数据的抽象模型，比如DOM树、树形控件等

js中没有树但是可以用 Object 和 Array 构建树

1）普通树

// 这就是一个常见的普通树形结构
const tree = {
  val: "a",
  children: [
    {
      val: "b",
      children: [
        {
          val: "d",
          children: [],
        },
        {
          val: "e",
          children: [],
        }
      ],
    },
    {
      val: "c",
      children: [
        {
          val: "f",
          children: [],
        },
        {
          val: "g",
          children: [],
        }
      ],
    }
  ],
}

> 深度优先遍历

尽可能深的搜索树的分支,就比如遇到一个节点就会直接去遍历他的子节点，不会立刻去遍历他的兄弟节点
口诀：
访问根节点
对根节点的 children 挨个进行深度优先遍历

// 深度优先遍历
const dfs = (tree) => {
  tree.children.forEach(dfs)
};

> 广度优先遍历

先访问离根节点最近的节点, 如果有兄弟节点就会先遍历兄弟节点，再去遍历自己的子节点
口诀
新建一个队列并把根节点入队
把队头出队并访问
把队头的children挨个入队
重复第二、三步直到队列为空

// 广度优先遍历
const bfs = (tree) => {
  const q = [tree];

  while (q.length > 0) {
    const n = q.shift()
    console.log(n.val);
    n.children.forEach(c => q.push(c))
  }
};

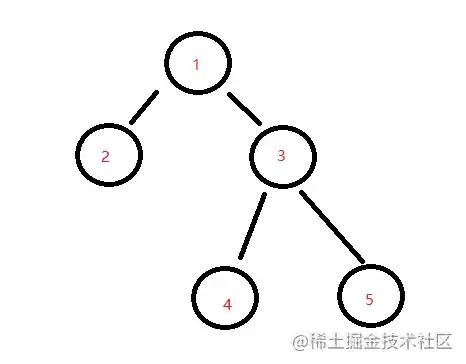
2）二叉树

树中每个节点 最多只能有两个子节点

 const bt = {
  val: 1,
  left: {
    val: 2,
    left: null,
    right: null
  },
  right: {
    val: 3,
    left: {
      val: 4,
      left: null,
      right: null
    },
    right: {
      val: 5,
      left: null,
      right: null
    }
  }
}

> 二叉树的先序遍历

访问根节点
对根节点的左子树进行先序遍历
对根节点的右子树进行先序遍历

// 先序遍历 递归
const preOrder = (tree) => {
  if (!tree) return

  console.log(tree.val);

  preOrder(tree.left);
  preOrder(tree.right);
}



// 先序遍历 非递归
const preOrder2 = (tree) => {
  if (!tree) return

  // 新建一个栈
  const stack = [tree];

  while (stack.length > 0) {
    const n = stack.pop();
    console.log(n.val);

    // 负负为正
    if (n.right) stack.push(n.right);
    if (n.left) stack.push(n.left);

  }
}

> 二叉树的中序遍历

对根节点的左子树进行中序遍历
访问根节点
对根节点的右子树进行中序遍历

// 中序遍历 递归
const inOrder = (tree) => {
  if (!tree) return;
  inOrder(tree.left)
  console.log(tree.val);
  inOrder(tree.right)
}


// 中序遍历 非递归
const inOrder2 = (tree) => {
  if (!tree) return;

  // 新建一个栈
  const stack = [];

  // 先遍历所有的左节点
  let p = tree;
  while (stack.length || p) {

    while (p) {
      stack.push(p)
      p = p.left
    }

    const n = stack.pop();
    console.log(n.val);

    p = n.right;
  }
}

> 二叉树的后序遍历

对根节点的左子树进行后序遍历
对根节点的右子树进行后序遍历
访问根节点

// 后序遍历 递归
const postOrder = (tree) => {
  if (!tree) return

  postOrder(tree.left)
  postOrder(tree.right)
  console.log(tree.val)
};



// 后序遍历 非递归
const postOrder2 = (tree) => {
  if (!tree) return

  const stack = [tree];
  const outputStack = [];

  while (stack.length) {
    const n = stack.pop();
    outputStack.push(n)
    // 负负为正
    if (n.left) stack.push(n.left);
    if (n.right) stack.push(n.right);

  }

  while (outputStack.length) {
    const n = outputStack.pop();
    console.log(n.val);
  }
};

> 二叉树的最大深度

// 给一个二叉树，需要你找出其最大的深度，从根节点到叶子节点的距离

// 时间复杂度 O(n) n为树的节点数
// 空间复杂度 有一个递归调用的栈 所以为 O(n) n也是为二叉树的最大深度
var maxDepth = function (root) {
  let res = 0;

  // 使用深度优先遍历
  const dfs = (n, l) => {
    if (!n) return;
    if (!n.left && !n.right) {
     // 没有叶子节点就把深度数量更新
      res = Math.max(res, l);
    }
    dfs(n.left, l + 1)
    dfs(n.right, l + 1)
  }

  dfs(root, 1)

  return res
}

> 二叉树的最小深度

// 给一个二叉树，需要你找出其最小的深度， 从根节点到叶子节点的距离


// 时间复杂度O(n) n是树的节点数量
// 空间复杂度O(n) n是树的节点数量
var minDepth = function (root) {
  if (!root) return 0

  // 使用广度优先遍历
  const q = [[root, 1]];

  while (q.length) {
    // 取出当前节点
    const [n, l] = q.shift();

    // 如果是叶子节点直接返回深度就可
    if (!n.left && !n.right) return l
    if (n.left) q.push([n.left, l + 1]);
    if (n.right) q.push([n.right, l + 1]);
  }

}

> 二叉树的层序遍历

// 需要返回 [[1], [2,3], [4,5]]


// 时间复杂度 O(n) n为树的节点数
// 空间复杂度 O(n) 
var levelOrder = function (root) {
  if (!root) return []

  // 广度优先遍历
  const q = [root];
  const res = [];
  while (q.length) {
    let len = q.length

    res.push([])

    // 循环每层的节点数量次
    while (len--) {
      const n = q.shift();

      res[res.length - 1].push(n.val)

      if (n.left) q.push(n.left);
      if (n.right) q.push(n.right);
    }

  }

  return res
};

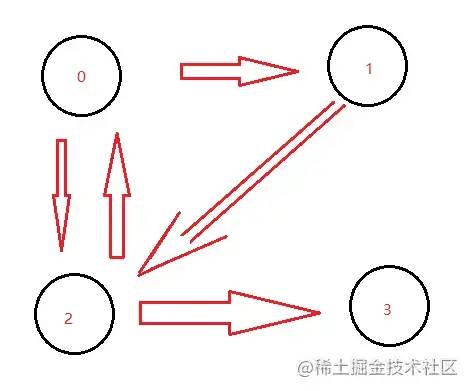
7 . 图

图是网络结构的抽象模型, 是一组由边连接的节点

js中可以利用Object和Array构建图

// 上图可以表示为
const graph = {
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3]
}


// 深度优先遍历，对根节点没访问过的相邻节点挨个进行遍历
{
    // 记录节点是否访问过
    const visited = new Set();
    const dfs = (n) => {
      visited.add(n);

      // 遍历相邻节点
      graph[n].forEach(c => {
        // 没访问过才可以，进行递归访问
        if(!visited.has(c)){
          dfs(c)
        }
      });
    }

    // 从2开始进行遍历
    dfs(2)
}


// 广度优先遍历 
{
    const visited = new Set();
    // 新建一个队列， 根节点入队， 设2为根节点
    const q = [2];
    visited.add(2)
    while (q.length) {

      // 队头出队，并访问
      const n = q.shift();
      console.log(n);
      graph[n].forEach(c => {

        // 对没访问过的相邻节点入队
        if (!visited.has(c)) {
          q.push(c)
          visited.add(c)
        }
      })
    }
}

1）有效数字

// 生成数字关系图 只有状态为 3 5 6 的时候才为一个数字
const graph = {
  0: { 'blank': 0, 'sign': 1, ".": 2, "digit": 6 },
  1: { "digit": 6, ".": 2 },
  2: { "digit": 3 },
  3: { "digit": 3, "e": 4 },
  4: { "digit": 5, "sign": 7 },
  5: { "digit": 5 },
  6: { "digit": 6, ".": 3, "e": 4 },
  7: { "digit": 5 },
}


// 时间复杂度 O(n) n是字符串长度
// 空间复杂度 O(1) 
var isNumber = function (s) {

  // 记录状态
  let state = 0;

  // 遍历字符串
  for (c of s.trim()) {
    // 把字符进行转换
    if (c >= '0' && c <= '9') {
      c = 'digit';
    } else if (c === " ") {
      c = 'blank';
    } else if (c === "+" || c === "-") {
      c = "sign";
    } else if (c === "E" || c === "e") {
      c = "e";
    }

    // 开始寻找图
    state = graph[state][c];

    // 如果最后是undefined就是错误
    if (state === undefined) return false
  }

  // 判断最后的结果是不是合法的数字
  if (state === 3 || state === 5 || state === 6) return true
  return false
};

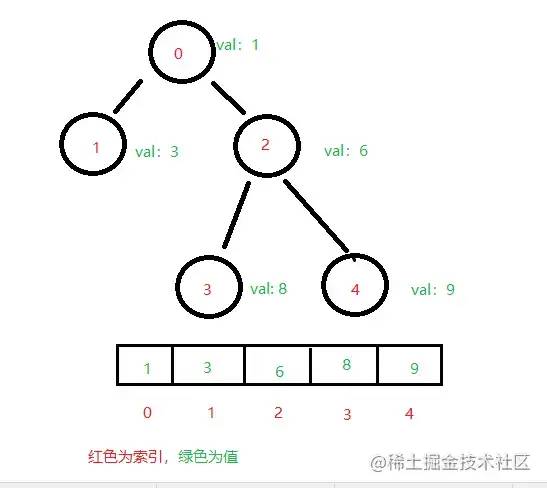
8 . 堆

一种特殊的完全二叉树, 所有的节点都大于等于最大堆,或者小于等于最小堆的子节点

js通常使用数组来表示堆

左侧子节点的位置是 2*index + 1
右侧子节点的位置是 2*index + 2
父节点的位置是 (index - 1) / 2 , 取余数

2）JS实现一个最小堆

// js实现最小堆类
class MinHeap {
  constructor() {
    // 元素容器
    this.heap = [];
  }

  // 交换节点的值
  swap(i1, i2) {
    [this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]]
  }

  //  获取父节点
  getParentIndex(index) {
    // 除以二， 取余数
    return (index - 1) >> 1;
  }

  // 获取左侧节点索引
  getLeftIndex(i) {
    return (i << 1) + 1;
  }

  // 获取右侧节点索引
  getRightIndex(i) {
    return (i << 1) + 2;
  }


  // 上移
  shiftUp(index) {
    if (index == 0) return;

    // 获取父节点
    const parentIndex = this.getParentIndex(index);

    // 如果父节点的值大于当前节点的值 就需要进行交换
    if (this.heap[parentIndex] > this.heap[index]) {
      this.swap(parentIndex, index);

      // 然后继续上移
      this.shiftUp(parentIndex);
    }
  }

  // 下移
  shiftDown(index) {
    // 获取左右节点索引
    const leftIndex = this.getLeftIndex(index);
    const rightIndex = this.getRightIndex(index);

    // 如果左子节点小于当前的值
    if (this.heap[leftIndex] < this.heap[index]) {

      // 进行节点交换
      this.swap(leftIndex, index);

      // 继续进行下移
      this.shiftDown(leftIndex)
    }

    // 如果右侧节点小于当前的值
    if (this.heap[rightIndex] < this.heap[index]) {
      this.swap(rightIndex, index);
      this.shiftDown(rightIndex)
    }
  }

  // 插入元素
  insert(value) {
    // 插入到堆的底部
    this.heap.push(value);

    // 然后上移： 将这个值和它的父节点进行交换，知道父节点小于等于这个插入的值
    this.shiftUp(this.heap.length - 1)
  }

  // 删除堆项
  pop() {

    // 把数组最后一位 转移到数组头部
    this.heap[0] = this.heap.pop();

    // 进行下移操作
    this.shiftDown(0);
  }

  // 获取堆顶元素
  peek() {
    return this.heap[0]
  }

  // 获取堆大小
  size() {
    return this.heap.length
  }

}

2）数组中的第k个最大元素

// 输入 [3,2,1,5,6,4] 和 k = 2
// 输出 5

// 时间复杂度 O(n * logK) K就是堆的大小
// 空间复杂度 O(K) K是参数k
var findKthLargest = function (nums, k) {

  // 使用上面js实现的最小堆类，来构建一个最小堆
  const h = new MinHeap();

  // 遍历数组
  nums.forEach(n => {

    // 把数组中的值依次插入到堆里
    h.insert(n);

    if (h.size() > k) {
      // 进行优胜劣汰
      h.pop();
    }
  })

  return h.peek()
};

3）前 K 个高频元素

// nums = [1,1,1,2,2,3], k = 2
// 输出: [1,2]


// 时间复杂度 O(n * logK) 
// 空间复杂度 O(k)
var topKFrequent = function (nums, k) {

  // 统计每个元素出现的频率
  const map = new Map();

  // 遍历数组 建立映射关系
  nums.forEach(n => {
    map.set(n, map.has(n) ? map.get(n) + 1 : 1);
  })

  // 建立最小堆
  const h = new MinHeap();

  // 遍历映射关系
  map.forEach((value, key) => {

    // 由于插入的元素结构发生了变化，所以需要对 最小堆的类 进行改造一下,改造的方法我会写到最后
    h.insert({ value, key })
    if (h.size() > k) {
      h.pop()
    }
  })
  return h.heap.map(item => item.key)
};

// 改造上移和下移操作即可
// shiftUp(index) {
//   if (index == 0) return;
//   const parentIndex = this.getParentIndex(index);
//   if (this.heap[parentIndex] && this.heap[parentIndex].value > this.heap[index].value) {
//     this.swap(parentIndex, index);
//     this.shiftUp(parentIndex);
//   }
// }
// shiftDown(index) {
//   const leftIndex = this.getLeftIndex(index);
//   const rightIndex = this.getRightIndex(index);

//   if (this.heap[leftIndex] && this.heap[leftIndex].value < this.heap[index].value) {
//     this.swap(leftIndex, index);
//     this.shiftDown(leftIndex)
//   }

//   if (this.heap[rightIndex] && this.heap[rightIndex].value < this.heap[index].value) {
//     this.swap(rightIndex, index);
//     this.shiftDown(rightIndex)
//   }
// }

四、常见算法及算法思想

1 . 排序

把某个乱序的数组变成升序序或者降序的数组， js比较常用sort方法进行排序

1）冒泡排序

比较所有相邻元素，如果第一个比第二个大就交换他们
执行一次后可以保证最后一个数字是最大的
重复执行 n-1 次，就可以完成排序

// 时间复杂度 O(n ^ 2) n为数组长度
// 空间复杂度 O(1)
Array.prototype.bubbleSort = function () {
  for (i = 0; i < this.length - 1; i++) {
    for (let j = 0; j < this.length - 1 - i; j++) {
      if (this[j] > this[j + 1]) {

        // 交换数据
        [this[j], this[j + 1]] = [this[j + 1], this[j]];
      }
    }
  }
}

2）选择排序

找到数组中最小的值,选中它并放到第一位
接着找到数组中第二小的值,选中它并放到第二位
重复上述步骤执行 n-1 次

// 时间复杂度：O(n ^ 2) n为数组长度
// 空间复杂度：O(1)
Array.prototype.selectionSort = function () {
  for (let i = 0; i < this.length - 1; i++) {
    let indexMin = i;

    for (let j = i; j < this.length; j++) {

      // 如果当前这个元素 小于最小值的下标 就更新最小值的下标
      if (this[j] < this[indexMin]) {
        indexMin = j;
      }
    }

    // 避免自己和自己进行交换
    if (indexMin !== i) {

      // 进行交换数据
      [this[i], this[indexMin]] = [this[indexMin], this[i]];
    }
  }
}

3）插入排序

从第二个数，开始往前比较
如它大就往后排
以此类推进行到最后一个数

// 时间复杂度 O(n ^ 2)
Array.prototype.insertionSort = function () {

  // 遍历数组 从第二个开始
  for (let i = 1; i < this.length; i++) {

    // 获取第二个元素
    const temp = this[i];

    let j = i;
    while (j > 0) {

      // 如果当前元素小于前一个元素 就开始往后移动
      if (this[j - 1] > temp) {
        this[j] = this[j - 1];
      } else {

        // 否则就跳出循环
        break
      }

      // 递减
      j--;
    }

    // 前一位置赋值为当前元素
    this[j] = temp;
  }
}

4）归并排序

分：把数组劈成两半 在递归的对子数组进行分操作，直到分成一个个单独的数
合：把两个树合并为有序数组，再对有序数组进行合并，直到全部子数组合并为一个完整的数组

// 时间复杂度 O(nlogn) 分需要劈开数组，所以是logn， 合则是n
// 空间复杂度 O(n)
Array.prototype.mergeSort = function () {

  const rec = (arr) => {
    // 递归终点
    if (arr.length === 1) return arr

    // 获取中间索引
    const mid = arr.length >> 1;

    // 通过中间下标,进行分割数组
    const left = arr.slice(0, mid);
    const right = arr.slice(mid);

    // 左边和右边的数组进行递归,会得到有序的左数组,和有序的右数组
    const orderLeft = rec(left);
    const orderRight = rec(right);


    // 存放结果的数组
    const res = [];


    while (orderLeft.length || orderRight.length) {

      // 如左边和右边数组都有值
      if (orderLeft.length && orderRight.length) {

        // 左边队头的值小于右边队头的值 就左边队头出队,否则就是右边队头出队
        res.push(orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift())
      } else if (orderLeft.length) {

        // 把左边的队头放入数组
        res.push(orderLeft.shift())
      } else if (orderRight.length) {

        // 把右边的队头放入数组
        res.push(orderRight.shift())
      }
    }

    return res
  }

  const res = rec(this)

  // 把结果放入原数组
  res.forEach((n, i) => this[i] = n)
}

> 合并两个有序链表

// 时间复杂度O(n) n为链表1和链表2的长度之和
// 空间复杂度O(1)
var mergeTwoLists = function (list1, list2) {

  // 新建一个新链表 作为返回值
  const res = {
    val: 0,
    next: null
  }

  // 指向新链表的指针
  let p = res;

  // 建立两个指针
  let p1 = list1;
  let p2 = list2;


  // 遍历两个链表
  while (p1 && p2) {

    // 如果链表1 小于 链表2的值 就接入链表1的值
    if (p1.val < p2.val) {
      p.next = p1;

      // 需要往后移动
      p1 = p1.next;
    } else {

      // 否则接入链表2的值
      p.next = p2;

      // 需要往后移动
      p2 = p2.next;
    }

    // p永远要往后移动一位
    p = p.next;
  }

  // 如果链表1或者链表2还有值,就把后面的值全部接入新链表
  if (p1) {
    p.next = p1;
  }
  if (p2) {
    p.next = p2;
  }

  return res.next;
};

5）快速排序

分区：从数组中任意选择一个基准，所有比基准小的元素放在基准前面，比基准大的元素放在基准后面
递归： 递归的对基准前后的子数组进行分区

// 时间复杂度 O(nlogN)
// 空间复杂度 O(1)
Array.prototype.quickSort = function () {
  const rec = (arr) => {

    // 如果数组长度小于等于1 就不用排序了
    if (arr.length <= 1) { return arr }

    // 存放基准前后的数组
    const left = [];
    const right = [];

    // 取基准
    const mid = arr[0];

    for (let i = 1; i < arr.length; i++) {

      // 如果当前值小于基准就放到基准前数组里面
      if (arr[i] < mid) {
        left.push(arr[i]);
      } else {

        // 否则就放到基准后数组里面
        right.push(arr[i]);
      }
    }

    // 递归调用两边的子数组
    return [...rec(left), mid, ...rec(right)];
  };

  const res = rec(this);
  res.forEach((n, i) => this[i] = n);
}

2 . 搜索

找出数组中某个元素的下标，js中通常使用indexOf方法进行搜索

1）顺序搜索

就比如indexOf方法， 从头开始搜索数组中的某个元素

2）二分搜索

从数组中的中间位置开始搜索，如果中间元素正好是目标值，则搜索结束
如果目标值大于或者小于中间元素，则在大于或者小于中间元素的那一半数组中搜索
数组必须是有序的，如不是则需要先进行排序

// 时间复杂度：O(log n)
// 空间复杂度：O(1)
Array.prototype.binarySearch = function (item) {
  // 代表数组的最小索引
  let low = 0;

  // 和最大索引
  let higt = this.length - 1;


  while (low <= higt) {

    // 获取中间元素索引
    const mid = (low + higt) >> 1;

    const element = this[mid];

    // 如果中间元素小于于要查找的元素 就把最小索引更新为中间索引的下一个
    if (element < item) {
      low = mid + 1
    } else if (element > item) {

    // 如果中间元素大于要查找的元素 就把最大索引更新为中间索引的前一个
      higt = mid - 1;
    } else {
      // 如果中间元素等于要查找的元素 就返回索引
      return mid;
    }
  }

  return -1
}

> 猜数字大小

// 时间复杂度 O(logn) 分割成两半的 基本都是logn
// 空间复杂度 O(1)
var guessNumber = function (n) {

  // 定义范围最小值和最大值
  const low = 1;
  const high = n;

  while (low <= high) {

    // 获取中间值
    const mid = (low + high) >>> 1;

    // 这个方法是 leetcode 中的方法
    // 如果返回值为-1 就是小了
    // 如果返回值为1  就是大了
    // 如果返回值为0  就是找到了 
    const res = guess(mid);

    // 剩下的操作就和二分搜索一样
    if (res === 0) {
      return mid
    } else if (res === 1) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }
};

3 . 分而治之

算法设计中的一种思想，将一个问题分成多个子问题，递归解决子问题，然后将子问题的解合并成最终的解

1）归并排序

分：把数组从中间一分为二
解：递归地对两个子数组进行归并排序
合：合并有序子数组

2）快速排序

分：选基准，按基准把数组分成两个子数组
解：递归地对两个子数组进行快速排序
合：对两个子数组进行合并

3）二分搜索

二分搜索也属于分而治之这种思想

> 分而治之思想：猜数字大小

// 时间复杂度 O(logn) 
// 空间复杂度 O(logn) 递归调用栈 所以是logn
var guessNumber = function (n) {

  // 递归函数 接受一个搜索范围
  const rec = (low, high) => {

    // 递归结束条件
    if (low > high) return;

    // 获取中间元素
    const mid = (low + high) >>> 1;

    // 判断是否猜对
    const res = guess(mid)

    // 猜对
    if (res === 0) {
      return mid
    } else if (res === 1) {
      // 猜大了
      return rec(mid + 1, high)
    } else {
      // 猜小了
      return rec(low, mid - 1)
    }
  }

  return rec(1, n)
};

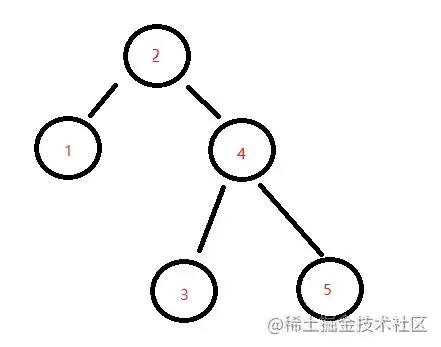
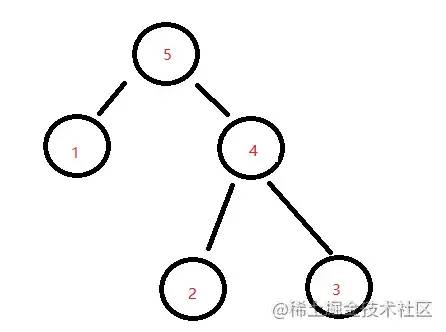
> 分而治之思想：翻转二叉树

// 时间复杂度 O(n) n为树的节点数量
// 空间复杂度 O(h) h为树的高度
var invertTree = function (root) {
  if (!root) return null
  return {
    val: root.val,
    left: invertTree(root.right),
    right: invertTree(root.left)
  }
};

> 分而治之思想：相同的树

// 时间复杂度 o(n) n为树的节点数量
// 空间复杂度 o(h) h为树的节点数
var isSameTree = function (p, q) {
  if (!p && !q) return true

  if (
    p && q
    && p.val === q.val
    && isSameTree(p.left, q.left)
    && isSameTree(p.right, q.right)
  ) return true

  return false
};

> 分而治之思想：对称二叉树

// 时间复杂度 O(n)
// 空间复杂度 O(n) 
var isSymmetric = function (root) {
  if (!root) return true
  const isMirror = (l, r) => {
    if (!l && !r) return true
    if (
      l && r 
      && l.val === r.val
      && isMirror(l.left, r.right)
      && isMirror(l.right, r.left)
    ) return true
    return false
  }

  return isMirror(root.left, root.right)
};

4 . 动态规划

动态规划是算法设计中的一种思想，将一个问题分解为相互重叠的子问题，通过反复求解子问题来解决原来的问题

1）斐波那契数列

// 时间复杂度 O(n) 
// 空间复杂度 O(n)
function fib(n) {
    let dp = [0, 1, 1];
    for (let i = 3; i <= n; i++) {

        // 当前值等于前两个值之和
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

2）爬楼梯

// 正在爬楼梯, 需要n阶才能到达楼顶
// 每次只能爬 1 或者 2 个台阶, 有多少中不同的方法可以到达楼顶

// 时间复杂度 O(n) n是楼梯长度
// 空间复杂度 O(1)
var climbStairs = function (n) {
    if (n < 2) return 1

    let dp0 = 1;
    let dp1 = 1

    for (let i = 2; i <= n; i++) {
        [dp0, dp1] = [dp1, dp1 + dp0]
    }

    return dp1
};

5 . 贪心算法

贪心算法是算法设计中的一种思想，期盼通过每个阶段的局部最优选择，从而达到全局的最优，但 结果并不一定是最优

1）分发饼干

// 每个孩子都有一个胃口g. 每个孩子只能拥有一个饼干
// 输入: g = [1,2,3], s = [1,1]
// 输出: 1
// 三个孩子胃口值分别是1,2,3  但是只有两个饼干,所以只能让胃口1的孩子满足

// 时间复杂度 O(nlogn) 
// 空间复杂度 O(1)
var findContentChildren = function (g, s) {
    // 对饼干和孩子胃口进行排序
    g.sort((a, b) => a - b)
    s.sort((a, b) => a - b)


    // 是第几个孩子
    let i = 0

    s.forEach((n) => {
        // 如果饼干能满足第一个孩子
        if (n >= g[i]) { 
            // 就开始满足第二个孩子
            i += 1
        }
    })

    return i
}

2）买卖股票的最佳时机Ⅱ

// 时间复杂度 O(n) n为股票的数量
// 空间复杂度 O(1)
var maxProfit = function (prices) {
  // 存放利润
  const profit = 0;
  for (let i = 1; i < prices.length; i++) {

    // 不贪 如有更高的利润就直接卖出
    if (prices[i] > prices[i - 1]) {
      profit += prices[i] - prices[i - 1]
    }
  }

  return profit
};

6 . 回溯算法

回溯算法是算法设计中的一种思想，一种渐进式寻找并构建问题解决方式的策略，会先从一个可能的动作开始解决问题，如不行，就回溯选择另外一个动作，直到找到一个解

1）全排列

// 输入 [1, 2, 3]
// 输出 [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]


// 时间复杂度 O(n!) n! = 1 * 2 * 3 * ··· * (n-1) * n;
// 空间复杂度 O(n)
var permute = function (nums) {
  // 存放结果
  const res = [];

  const backTrack = (path) => {
    // 递归结束条件 
    if (path.length === nums.length) {
      res.push(path)
      return
    }

    // 遍历传入数组
    nums.forEach(n => {
      // 如果子数组中有这个元素就是死路， 需要回溯回去走其他路
      if (path.includes(n)) return;

      // 加入到子数组里
      backTrack(path.concat(n))
    })
  }

  backTrack([])

  return res;
};

2）子集

// 输入 [1,2,3]
// 输出 [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

// 时间复杂度 O(2 ^ N) 每个元素都有两种可能
// 空间复杂度 O(N)
var subsets = function (nums) {
  // 存放结果数组
  const res = [];

  const backTrack = (path, l, start) => {
    // 递归结束条件
    if (path.length === l) {
      res.push(path)
      return
    }

    // 遍历输入的数组长度 起始位置是start
    for (let i = start; i < nums.length; i++) {

      // 递归调用 需要保证子集的有序, start为 i+1
      backTrack(path.concat(nums[i]), l, i + 1)
    }
  };

  // 遍历输入数组长度
  for (let i = 0; i <= nums.length; i++) {

    // 传入长度 起始索引
    backTrack([], i, 0)
  }


  return res
};

五、结语

本文中，仅对常见和常用的数据结构与算法进行了演示

算法这个东西，平时还是要多练。记得看完后多刷一刷leetcode

如果本文对你有帮助，记得点赞和关注❤️

万字总结 JS 数据结构与常用的算法

一、前言

二、基本概念

1 . 时间复杂度

2 . 空间复杂度

三、数据结构

1 . 栈

1）十进制转二进制

2）判断字符串的有效括号

2 . 队列

1）最近的请求次数

3 . 链表

1）手写instanceOf

2）删除链表中的节点

3）删除排序链表中的重复元素

4）反转链表

4 . 集合

1）去重

2）两个数组的交集

5 . 字典

1）两数之和

2）两个数组的交集

3）字符的有效的括号

4）最小覆盖字串

6 . 树

1）普通树

> 深度优先遍历

> 广度优先遍历

2）二叉树

> 二叉树的先序遍历

> 二叉树的中序遍历

> 二叉树的后序遍历

> 二叉树的最大深度

> 二叉树的最小深度

> 二叉树的层序遍历

7 . 图

1）有效数字

8 . 堆

2）JS实现一个最小堆

2）数组中的第k个最大元素

3）前 K 个高频元素

四、常见算法及算法思想

1 . 排序

1）冒泡排序

2）选择排序

3）插入排序

4）归并排序

> 合并两个有序链表

5）快速排序

2 . 搜索

1）顺序搜索

2）二分搜索

> 猜数字大小

3 . 分而治之

1）归并排序

2）快速排序

3）二分搜索

> 分而治之思想：猜数字大小

> 分而治之思想：翻转二叉树

> 分而治之思想：相同的树

> 分而治之思想：对称二叉树

4 . 动态规划

1）斐波那契数列

2）爬楼梯

5 . 贪心算法

1）分发饼干

2）买卖股票的最佳时机Ⅱ

6 . 回溯算法

1）全排列

2）子集

五、结语