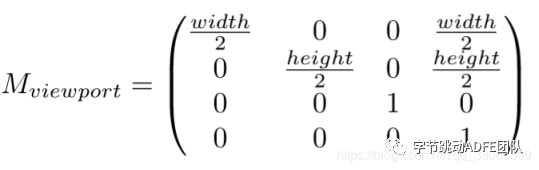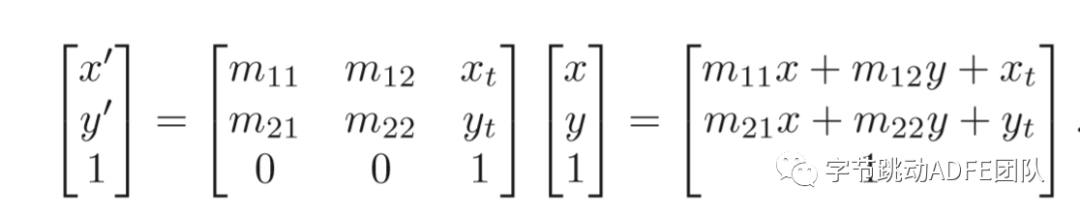图形渲染入门窥径( 前端视角 + 科普向 )
/ 关于 & 介绍 /
图形渲染的内容在前端的整个知识体系当中占据着不可或缺的一部分,无论是数据可视化、3D 模型展示、H5 游戏开发都需要对图形渲染方面的知识有所了解。
本文既从前端视角出发,来对图形渲染方面的入门知识做一些粗浅的科普,并实际动手完成在浏览器当中渲染一个简单的 3D 模型。
/ 渲染 /
在代码实现过程中包含许多数据模型与数学算法,为避免在开始实现之前抛出太多概念影响整体学习流程,因此只有在使用某个数据或算法时才会展开进行讲解。
1
2D 色块渲染
每一个 3d 模型大抵都是由许多的三角形面组成的( 哪怕有些输出的模型并非三角形面,也可以将一个多边形面转化多个三角形面,即三角形是最简单的平面,而诸多平面的组合构成一个模型 )。
每一个三角形面,都是由三个顶点组成的,换句话说,一个模型就是由多个顶点组成的,所以在渲染的过程中,我们核心关注的内容,就是顶点的变化与渲染。
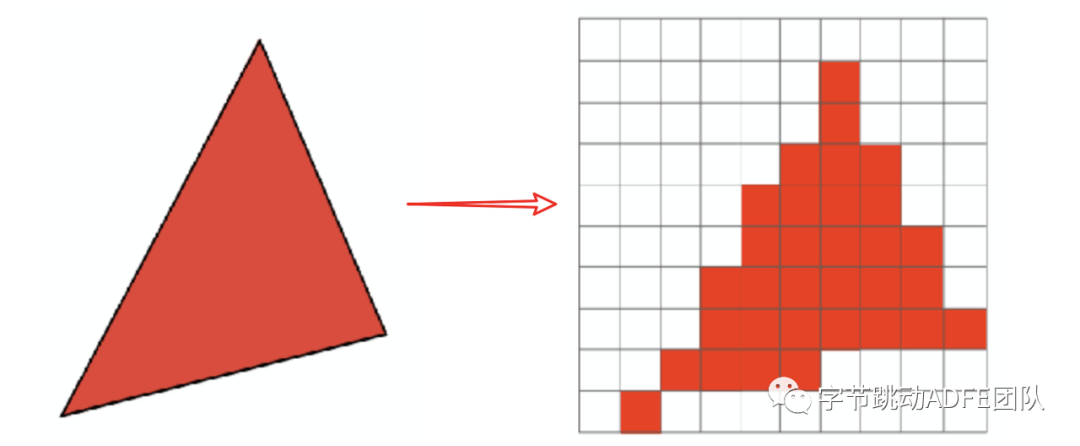
下方是一个例子,来展示如何渲染一个简单的三角形。
// 一些类与方法会放到整体流程下方讲解
function renderPlane() {
// canvas 基本信息获取
const canvas = document.getElementById("renderCanvas") as HTMLCanvasElement;
const ctx = canvas.getContext("2d");
// canvas 的宽高决定了绘制像素的数量
const width = canvas.width;
const height = canvas.height;
// 以原始坐标 [-1, 1] 来定义随意定义一个三角形的三个顶点
const v1 = new Vertex();
// Vertex 代表顶点类:存储位置信息( position )、法向量、颜色、UV 坐标等信息
v1.position = new Vec4(0, 0.2, 0, 1);
const v2 = new Vertex();
v2.position = new Vec4(-0.2, -0.2, 0, 1);
const v3 = new Vertex();
v3.position = new Vec4(0.2, -0.2, 0, 1);
/**
视口变换: 将标准平面映射到屏幕分辨率范围之内
即,将 [-1, 1]^2 坐标映射到 [0, width]*[0, height] 组成的坐标系
在 canvas 环境中,width & height 即为 canvas.width & canvas.height
简单来说就是将某一个坐标系当中的点,映射到另一个坐标系当中
*/
// 转换为视口坐标,具体方法下方会详细阐述
const viewPosition1 = getViewPortPosition(v1.position);
const viewPosition2 = getViewPortPosition(v2.position);
const viewPosition3 = getViewPortPosition(v3.position);
/**
图片信息: ctx.createImageData(width, height)
以一个 width, height = 1 的 canvas 举例,其 imageData 为 Uint8ClampedArray
ImageData: {
data: {
0: 255, R 值
1: 0, G 值
2: 0, B 值
3: 255, A 值
},
colorSpace: "srgb", 颜色类型
height: 1,
width: 1,
}
其中 data 为颜色信息,具体类型为 Uint8ClampedArray
*/
const imageData = ctx.createImageData(width, height);
/**
至此,我们获得了当前 canvas 的上所有的像素信息
借助当前 canvas 的 width, height 创建一个 buffer 对象
对于每一个实际被渲染的图像( 对于 canvas 来说就是通过 putImageData 来创建的图像 ),
都存在一个缓冲帧对象 ( FrameBuffer ),用于存储下一次需要被渲染出来的图像数据信息
FrameBuffer 当中存储着与 ImageData.data 对应的颜色数组信息、宽高信息,初识色( 清除色 )
通过 x y 来索引颜色数组中的位置,对单个像素颜色进行赋值
*/
const buffer = new FrameBuffer(width, height);
// 初始数据
buffer.setFrameBuffer(imageData.data);
buffer.setClearColor(Color.BLACK);
// 遍历整个画布,获取对应像素坐标,进行赋值 ( 下方会讲解优化方法 )
for (let x = 0; x < width; x++) {
for (let y = 0; y < height; y++) {
// 判断是否在三角形内 --> 像素坐标偏移 0.5 以对其像素中心点
const curposition = new Vec4(x + 0.5, y + 0.5, 0, 1);
// 通过叉乘判断当前坐标点是否位于三角形内部
const isInner = isTriangleInner(curposition, viewPosition1, viewPosition2, viewPosition3);
// 如果当前点位于三角形内部,就给当前坐标像素赋予一个颜色
isInner && buffer.setColor(x, y, Color.RED);
}
}
// 写入像素数据
ctx.putImageData(imageData, 0, 0);
};至此,我们就能绘制出一个简单的三角形了,其中仍有许多待优化的点与遗漏处,在下方会逐渐补充
我们先来看一下一些被抽象的算法是如何实现的
1. 视口变换
先来看一下视口变换做的事情:
- 将坐标原点从 [-1, 1] [-1, 1] 的 [0, 0] 原点移动到 [0, width] [0, height] 的[0, 0] 原点
- 将坐标系的 X, Y 坐标( 宽高 )从 [-1, 1]^2 变换为 width & height
简单来说就是将一个宽度与长度为 2 的矩形,通过缩放与位移的方式变换为一个宽高为 width & height 的矩形,通过矩阵的表示方式,即为
接下来简单实现一下
/**
当前函数接受一个由向量表示的坐标,内部包含一个如上表示的 4*4 矩阵
两者相乘,返回一个新的坐标向量
向量: 即一个 1*4 的矩阵 [x, y, z, w], w 的作用是为了辅助位移运算,如上图矩阵所示
矩阵: 在图形学当中多用 4*4 的矩阵
a1 a2 a3 a4
b1 b2 b3 b4
c1 c2 c3 c4
d1 d2 d3 d4
*/
function getViewPortPosition (vector) {
// width = canvas.width; height = canvas.height;
const matrix = new Matrix(
width / 2, 0, 0, width / 2,
0, -height / 2, 0, height / 2,
0, 0, 1, 0,
0, 0, 0, 1
);
// 向量与矩阵相乘, 返回一个新的向量坐标
return vec4MulMat4(vector, matrix);
}向量 * 矩阵示例 ---> 返回一个新的向量
2. 通过叉乘判断当前坐标点是否位于三角形内部
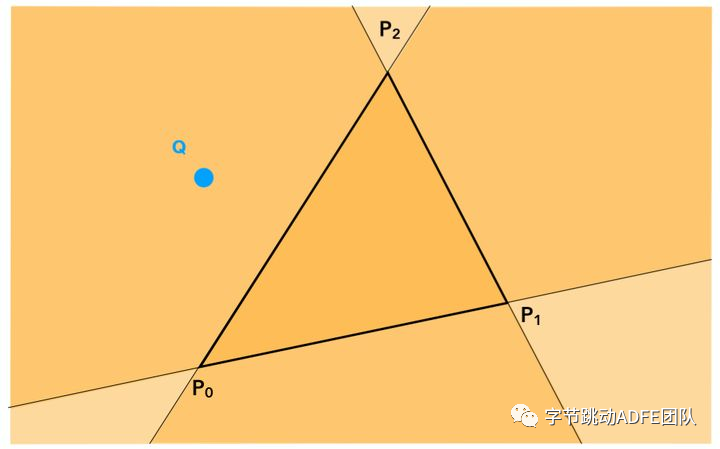
通过当前坐标( 向量 )与三角形的三个边( 向量 ) 分别进行叉乘计算,如果符号相同,证明与三个向量处于同侧,即该点位于三角形内部,下方会给出另一种更通用的判断方式,此处的计算方式简单了解原理即可
2
3D 模型渲染
至此我们对于如何渲染一个基础的三角形有了简单的了解,但其中依然饱含许多困惑,比如
- 对于包含诸多三角形的一个模型,每渲染一个面,都需要重新完全遍历一次画布,显然是十分浪费的。
- 如果观察仔细的话,会发现三角形边缘存在着非常明显的锯齿状,是什么导致的,如果进行优化
- 我们能获取到顶点的 x y 坐标,进而在纹理图片当中查找对应的颜色,那么在一个面当中的那些像素坐标,如果确定其 x y 坐标
- 如何将一个 3d 模型转换为一个可以渲染的 2d 图像,其中的透视与遮挡关系如何处理
我们先来逐一对这些问题进行解决,然后再
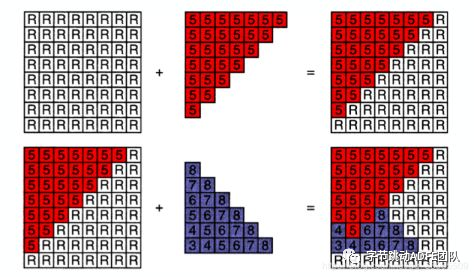
1. 盒包围模型: 通过确定一个三角形( 或多个三角形 )的最大与最小 X Y 值,来圈定一个更小的遍历范围
const boundBox = getBoundBox(position1, position2, position3);
for (let x = boundBox.minX; x < boundBox.maxX; x++) {
for (let y = boundBox.minY; y < boundBox.maxY; y++) {
....
}
}2. 抗锯齿: 结合实际场景,出现锯齿的原因很好理解,即单个像素的显示过大,或者说单纯的通过某个像素点来确定一个像素的显示颜色,并不能完全的说明该像素点所包含的全部颜色信息。
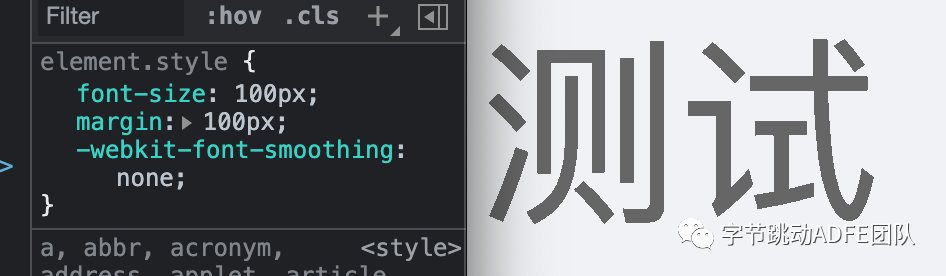
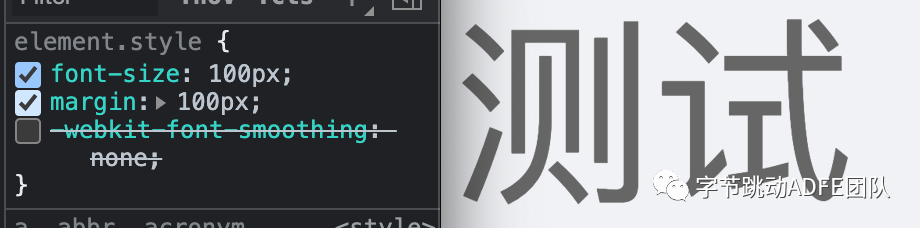
这在我们日常前端开发中也会遇到,如果我们为某个元素设置 font-smoothing: none 的话,就会发现该元素下的字体会出现明显的锯齿化
在实际应用当中,抗锯齿有多种方式与手段,适用于不同的场景。此处介绍一种简单的抗锯齿方式供大家了解
多采样反走样( Multi-Sampling Anti-Aliasing )
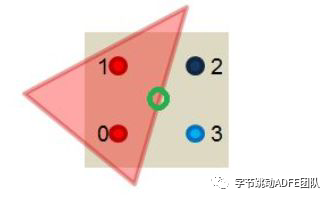
在原本的绘制过程中,当一条路径覆盖过某一个像素时,通过查看像素中心点是否在路径内侧( 图形内 ),即可判断是否需要为这个像素点着色,而在两个图像相交的边缘,一个像素需要承担更多的责任,即两个图形之间的过渡信息。
那么仅仅依靠中心点覆盖( true or false )是无法完成这种过滤情况的表述的,按照( 增加采样的频率 )思路大纲,我们将一个像素中划分四个采样点,通过判断一个( 路径 )或图形覆盖了几个像素点,如覆盖了两个像素点则透明度表达为 50%,三个就为 75%,就可以在一定程度上的表述出这种过渡关系,使得图形边缘看起来更加平滑
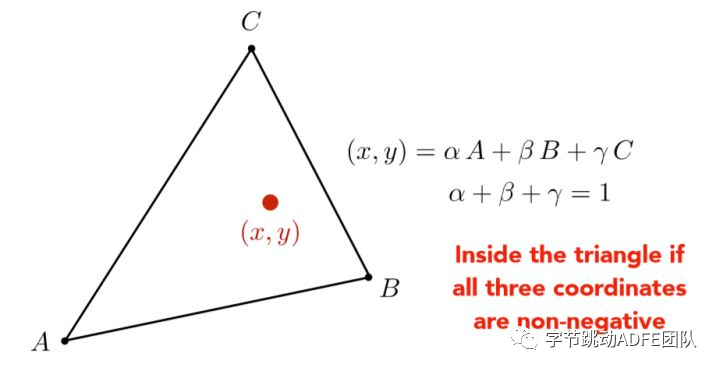
3. 插值计算: 通过计算重心坐标的方式,确定三个顶点内某个点的数据信息
如确定一个线段内的某一点一样,我们可以通过三点加权的形式,来表述某一点,通过此方式也可以确定该点是否位于此三个顶点组成平面内。
// 存在由 (x1, y1) 与 (x2, y2) 构成的一个线段,如何表示线段其中一点
(x, y) = a(x1, y1) + b(x2, y2)4. 相机介绍( 视图变换 )
通过引入相机,将 3d 坐标( 模型数据坐标 x y z )转换为 2d 坐标 ( 相机可见坐标 x y ),总体分为下述三个步骤,以及一个上方已经介绍过的视口变换
- 模型变换: 简单来说就是调整摆放模型的位置
- 相机变换: 获取从相机角度观测物体得到的相对位置
- 投影变换( 此处仅讲解通常使用到的透视投影 ): 将物品如投影一般,把物体顶点的 3d 坐标映射到一个 [-1, 1]^2 的 2d 平面当中,同时保留其顶点 z 坐标用于计算遮挡关系( 每一个像素的 z 坐标可以通过三个顶点的重心坐标运算出来 )
最后再通过上方介绍的视口变换的方式,将物体从 [-1, 1]^2 的坐标系展开至 [0, width] * [0, height] 当中,即可完成整个视图变换过程
相机变换
下方是一个代码形式的简述,来表述一个相机的创建与运算过程
class Camera {
// 当前相机所在的位置坐标,通过一个向量进行表示,如 (10, 10, 20)
position;
// 相机的朝向,在应用相机时,使得相机看向某一个坐标点,以运算出相机的朝向向量
direct;
// 相机的向上方向向量,确定相机的正反
up;
// 接受一个坐标,该坐标即是物体坐标,即相机要看向的坐标点
lookAt(point) {
....
}
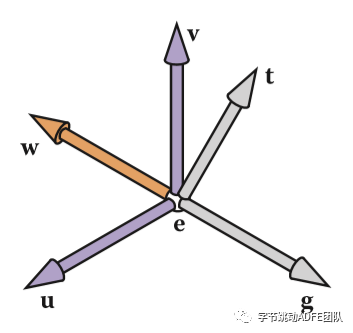
}首先来看一下如何计算相机的几个向量,也就是相机的三个相互垂直的坐标
// 通过设置相机的位置与物体的位置,我们可以通过两个坐标相减直接计算出 direct 向量
this.direct =
point.x - this.position.x,
point.y - this.position.y,
point.z - this.position.z
// 通过坐标相见,计算并设置 direct 向量( 同时对该向量进行单位化,即保证单位坐标向量长度为一 )
const unitLength = x*x + y*y + z*z + w*w
this.x = x / Math.sqrt(unitLength);
...
/**
通过设置临时 Y 轴辅助 up 向量,与 direct 向量进行叉乘,计算出 x 轴向量,
再通过 x 轴向量与 direct 向量,计算出实际 up 向量,同时坐标向量都需要注意单位化 --- 长度为1
*/
this.up = vectorMultiply(XCoordinate, this.direct).normalize();至此,我们获得了计算必须的相机位置坐标,物体位置坐标,相机朝向物体向量,相机的 up 向量
接下来,我们要将相机位置移动 & 旋转回世界坐标原点( 即将相机坐标与世界坐标对齐 ),就可以获取到相机观测物体( 物体本身坐标应用为世界坐标 )的相对位置了
// 将坐标移动回原点
1, 0, 0, -this.position.x,
0, 1, 0, -this.position.y,
0, 0, 1, -this.position.z,
0, 0, 0, 1,此时相机的坐标原点与世界坐标原点已经对齐,仅需要做一次旋转操作,就可以使两个坐标完全重合了
因为此时我们求解的是旋转的变换矩阵,即有性质为
当前矩阵 · 变换矩阵 = I 矩阵
变换矩阵 = 逆矩阵 = 转置矩阵 (因为: 正交矩阵)
所以,仅需要对当前坐标进行一次转置,即可求出对应的变换矩阵
(
XCoordinate.x, this.up.x, -this.direct.x, 0,
XCoordinate.y, this.up.y, -this.direct.y, 0,
XCoordinate.z, this.up.z, -this.direct.z, 0,
0, 0, 0, 1,
).transpose();至此,我们已经解决了物体与相机直接的相对位置了,即物体的变换矩阵,下面就需要将通过变换的坐标顶点映射到一个 [-1, 1]^2 的坐标系当中了 ( 透视投影变换 )
透视投影变换
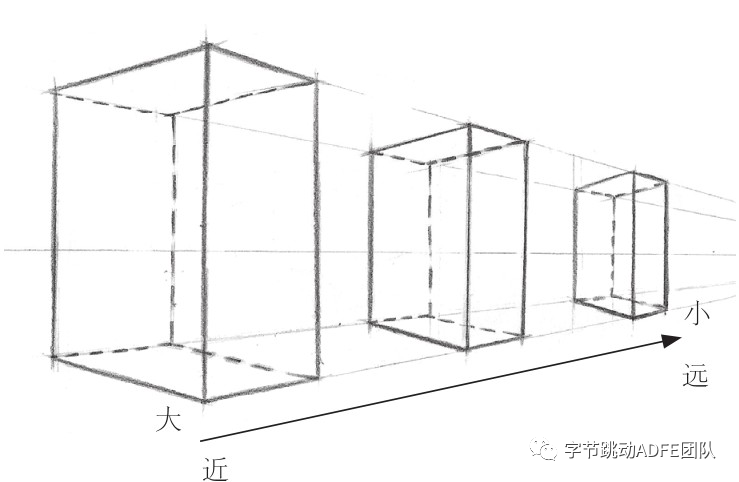
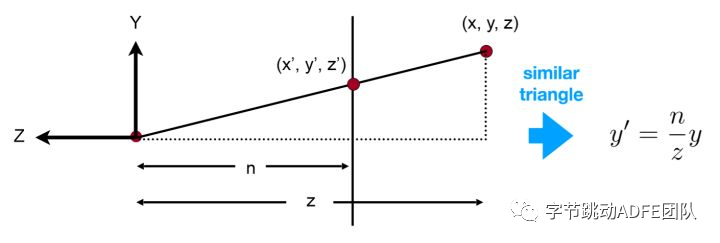
因为人眼在观测物体时,存在近大远小的关系,而这个比率可以被计算所得
只需要如图定义一个 n 值与 z 值,我们就可以凭借这个比例,将坐标关系映射出来,同时将 z 点记录,留作深度测试使用( 判断前后遮挡关系 )
最终获得对应矩阵关系如下
如需要重新将图像压缩回 [-1, 1]^2 的标准坐标,则对应变换矩阵如下所示,实际使用时将其按照上方介绍的视口变换展开即可获取到对应视口当中的 x y 坐标
深度测试( z buffer )
截止此处,我们可以获得到一个不包含遮挡关系的 2d 图形,距离将图形正确的渲染出来,只差最后一步对于遮挡关系的处理,我们此时已知,渲染图形,就是赋予像素其对应的颜色,那么为了处理遮挡关系,我们为每一个像素点,保存一个 index 值,储存当前 z 值与颜色信息,如果下面的 z 值大于当前所保存的 z 值,则进行替换,即始终保存最大的 z 值与颜色
class ZBuffer {
frameBuffer // 用于存储颜色信息,同 ImageData.data
z // 存放 z 值数组
constructor() {
this.z = new Float32Array(canvas.width * canvas.height).fill(NaN);
}
}整理流程
function renderObj() {
/**
对应 obj 物体模型文件数据格式如下
# object 1
v -0.500000 -0.500000 0.500000
v 0.500000 -0.500000 0.500000
v -0.500000 0.500000 0.500000
vt 0.000000 0.000000
vt 1.000000 0.000000
vt 0.000000 1.000000
vn 0.000000 0.000000 1.000000
vn 0.000000 0.000000 1.000000
vn 0.000000 0.000000 1.000000
f 1/1/1 2/2/2 3/3/3
{
face: [], // index
v: [], // position
n: [], // 法向量
t: [], // 纹理坐标 x = vt.x y = 1-vt.y
}
*/
// 模型与纹理引入
const model = loadModel();
model.setMapTexture(key, loadTextureImage());
// 创建模型体
const obj = new ModelObject(model);
// 初始化相机,并计算变换矩阵
const camera = new Camera(10, 10, 20).lookAt(obj.position);
// 创建 z buffer
const zBuffer = new ZBuffer(canvas.width, canvas.height);
// 图形渲染
const mat = mat4MulLinked([
node.getPositionMat4(),
camera.translte,
camera.getPerspectiveMat4(),
])
for (let i = 0, len = model.face.length; i < len; i++) {
// 获取面信息
const face = model.face[i];
// 获取纹理信息
const texture = model.mat.get(face.key);
// 通过顶点坐标计算包围盒模型
...
const boundBox = getBoundBox(v1, v2, v3);
// 通过包围盒来确立遍历范围
for (let x = boundBox.minX; x < boundBox.maxX; x++) {
for (let y = boundBox.minY; y < boundBox.maxY; y++) {
// 计算重心坐标
const barycentric = getBarycentric(x+0.5, y+0.5, v1, v2, v3);
// 不在三角形范围内则不进行计算
if (barycentric.x < 0 || barycentric.y < 0 || barycentric.z < 0) {
continue;
}
// 获取当前坐标存储的 z 值
const z = getViewPositionZByBarycentric(v1, v2, v3, barycentric);
// 如果 z 值小则跳过
if (!zBuffer.depthTest(x, y, z)) {
continue;
}
// 反之则进行记录
zbuffer.set(x, y, z);
// 通过对应 uv 坐标获取纹理图片上的对应颜色信息
const u = getUByBarycentric();
const v = getVByBarycentric();
const color = texture.getColorByUV(u, v);
// 设置对应颜色信息
buffer.setColor(x, y, color);
}
}
}
// 写入图像信息
ctx.putImageData(imageData, 0, 0);
}