LeetCode通关：求次数有妙招，位运算三连

316次阅读  |  发布于2年以前

大家好，我是刷题困难户老三，这一节我们来刷几道很有意思的求次数问题，它们都有同一类非常巧妙的解法。

这种解法是什么呢？往下看吧！

基础知识

在开始之前，我们最好先了解一些位运算的基础知识。

原反补码

先简单说一下，原码、反码、补码。

一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.

比如，十进制中的数 +3 ，假如计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。

原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

❝[+1]原 = 0000 0001

[-1]原 = 1000 0001

❞

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。

❝[+1] = [00000001]原 = [00000001]反

[-1] = [10000001]原 = [11111110]反

❞

正数的补码就是其本身

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

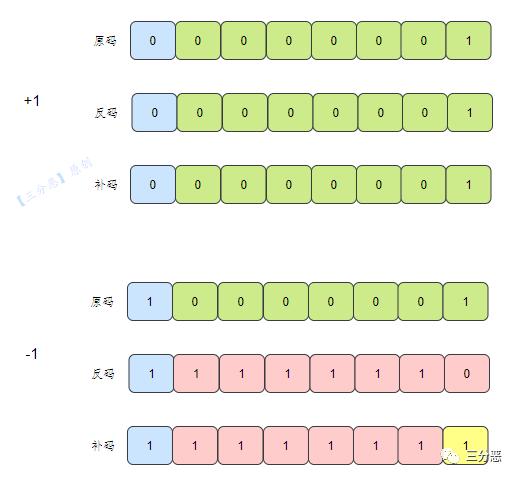
❝[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1] = [10000001]原 = [11111110]反 = [11111111]补

❞

补码是人脑认识里不太直观的一种表示方式，之所以发明补码，是为了让机器以一种一致的方式来处理加法运算。

原反补码

更多知识建议阅读《j计算机组成原理》。

与或非异或运算

在处理整型数值时，位运算符可以直接对组成整型数值的各个位进行操作。这些位运算符在位模式下工作。位运算符包括：&、|、~、^

对应位都为1，结果为1，否则结果为0

int a=129;
int b=128;
System.out.println("a与b的结果："+(a&b));
# 输出
a与b的结果：128

计算过程如下:

10000001 &
10000000 =
10000000

对应位只要有一个为1，结果是1，否则就为0

int a=129;
int b=128;
System.out.println("a或b的结果："+(a|b));
# 输出
a或b的结果是：129

计算过程如下:

10000001 |
10000000 =
10000001

位为0，结果是1；位为1，结果是0

 int a = 8;
System.out.println("非a的结果："+(~a));
# 输出
非a的结果：-9

计算过程如下

        //8转换为二进制
        1000
        // 补符号位
        01000
        // 取反
        10111 (补码)
        // 转源码除符号位取反+1
        11001

对应位相同，结果是0，否则结果是1

1111 ^
0010 =
1101

移位运算

移位运算见名知意，是数字二进位的移动，我们这里只讨论int型的移位运算。

数值的补码全部左移若干位，符号位和高位丢弃，低位补 0。

数值的补码全部右移若干位，符号位不变。

假如int是8位二进制，两个例子如下：

10的补码为0000 1010，左移一位变成20（0001 0100），右移一位变成5（0000 0101）

5的补码为0000 0101，左移一位变成10（0000 1010），右移一位变成2（0000 0010）

求次数问题

LeetCode136. 只出现一次的数字

☕ 题目：136. 只出现一次的数字 (https://leetcode-cn.com/problems/single-number/)

❓ 难度：简单

描述：

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

题目示例

思路：

「哈希法」

用哈希表存储每一个元素出现的次数，最后找到出现一次的元素。

代码如下：

    public int singleNumber(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        //存储元素出现的次数
        for (int i = 0; i < nums.length; i++) {
            map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        }
        //遍历获取出现次数为1的情况
        for (int k : map.keySet()) {
            if (map.get(k) == 1) {
                return k;
            }
        }
        return -1;
    }

⏰ 时间复杂度：O(n)

空间复杂度：O(n)

「位运算」

题中要求空间复杂度O(1)，哈希法明显是不合要求的。

这里有一个全新的方法：位运算。

异或运算有如下特点：

可以重复分利用异或运算的特性，异或数组所有元素，最后留下的那个就是只出现一次的元素。

    public int singleNumber(int[] nums) {
        int ans = 0;
        for (int i = 0; i < nums.length; i++) {
            //异或运算
            ans ^= nums[i];
        }
        return ans;
    }

⏰ 时间复杂度：O(n)

空间复杂度：O(1)

LeetCode137. 只出现一次的数字 II

☕ 题目：137. 只出现一次的数字 II (https://leetcode-cn.com/problems/single-number-ii/)

❓ 难度：中等

描述：

给你一个整数数组 nums ，除某个元素仅出现 「一次」 外，其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。

题目示例

这道题和 剑指 Offer 56 - II. 数组中数字出现的次数 II 是一样的。

思路：

「哈希法」

第一反应还是哈希法，不用多说了，直接上代码：

   public int singleNumber(int[] nums) {
        if (nums.length == 1) {
            return nums[0];
        }
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        }
        for (int k : map.keySet()) {
            if (map.get(k) == 1) {
                return k;
            }
        }
        return -1;
    }

⏰ 时间复杂度：O(n)

空间复杂度：O(n)

「位运算」

好了，又到了我们的主角出场。

将我们的数的二进制位每一位相加，然后对每一位的和与3取余：

位运算

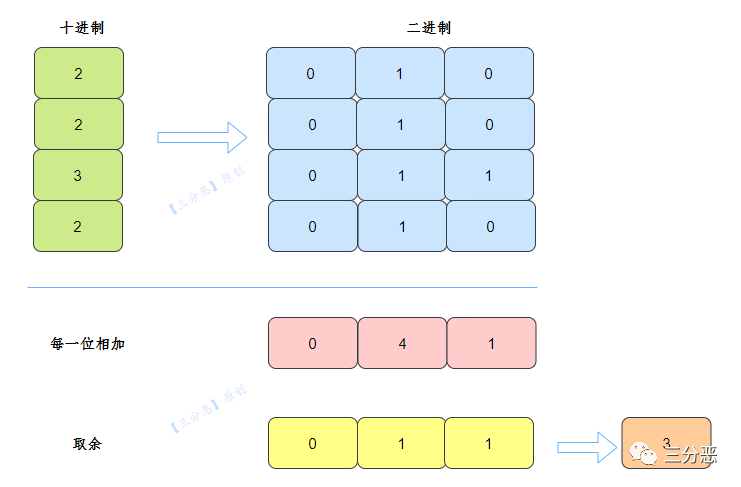
这个原理是什么呢？

如果其他数都出现 3 次，只有目标数出现 1 次，那么每一位的 1 的个数无非有这两种情况，

这个 3 的倍数 +1 的情况也就是我们的目标数的那一位。

代码如下：

   public int singleNumber(int[] nums) {
        int res = 0;
        for (int i = 0; i < 32; i++) {
            int count = 0;
            for (int num : nums) {
                //检查第i位是否为1
                if ((num >> i & 1) == 1) {
                    count++;
                }
            }
            if (count % 3 != 0) {
                //将第i位设为1
                res = res | 1 << i;
            }
        }
        return res;
    }

时间复杂度：O(n)

空间复杂度：O(1)

LeetCode260. 只出现一次的数字 III

☕ 题目：260. 只出现一次的数字 III (https://leetcode-cn.com/problems/single-number-iii/)

❓ 难度：中等

描述：

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

题目示例

这道题和 剑指 Offer 56 - I. 数组中数字出现的次数 是一模一样的。

思路：

这次不是一个重复的元素了，是两个。还是先上我们朴素的哈希法。

「哈希法」

代码如下：

    public int[] singleNumber(int[] nums) {
        int[] res = new int[2];
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        }
        int index = 0;
        for (int k : map.keySet()) {
            if (map.get(k) == 1) {
                res[index] = k;
                index++;
            }
        }
        return res;
    }

时间复杂度：O(n)

空间复杂度：O(n)

「位运算」[5]

我们在 LeetCode136. 只出现一次的数字 里只用了一个「异或」就找出了那个出现一次的数字。

这道题怎么办呢？

要是我们能把它分成两组就好了。

怎么分呢？

大家都知道异或运算对应位相同，结果是0，否则结果是1

我们可以根据两个数某一位是否是0和1来把数组分为两组。

例如数组：[12，13，14，17，14，12]

异或的结果是：13^17。

获取分组位

分组位找到了。

那么怎么借助分组位进行分组呢？

13、17的异或值，可以仅保留异或值的分组位，其余位变为 0，例如 11100变成00100。

为什么要这么做呢？在第二题提到，我们可以根据 a & 1 来判断 a 的最后一位为 0 还是为 1，所以我们将 11100变成00100之后，然后数组内的元素 x & 001 即可对 x 进行分组 。

那么我们如何才能仅保留分组位，其余位变为 0 呢？

可以利用 x & (-x) 来保留最右边的 1。

代码如下：

   public int[] singleNumber(int[] nums) {
        int bitMask = 0;
        //把数组中的所有元素全部异或一遍
        for (int num : nums) {
            bitMask ^= num;
        }
        //保留最右边的1
        bitMask &= -bitMask;
        int[] res = {0, 0};
        for (int num : nums) {
            //将数组分成两部分，每部分分别异或
            if ((num & bitMask) == 0) {
                res[0] ^= num;
            } else {
                res[1] ^= num;
            }
        }
        return res;
    }

总结

三道求次数问题就这么做完了。

求次数问题的朴素做法是Hash法，使用Hash存储元素出现次数。

但是Hash法空间复杂度是O(n)，如果要求O(1)的空间复杂度就不行了。

这时候就要灵活利用位运算的方法，位运算的关键在于充分了解位运算的相关应用。

博主算法练习生一枚，刷题路线和思路主要参考如下！

参考：

Copyright© 2013-2020

All Rights Reserved 京ICP备2023019179号-8