手写了一个正则表达式引擎

大家好， 相信正则表达式大家都很熟悉，但你知道正则表达式匹配过程是如何实现的吗？要想知道这个过程莫过于自己动手写一个正则表达式引擎。

为方便起见，我们的引擎只支持点号"."以及星号"*"的正则表达式匹配，即：

• '.'匹配任何单个字符
• '*'匹配0个或者多个前一个字符

示例：

输入: s = "aa", p = "a*"
输出: true
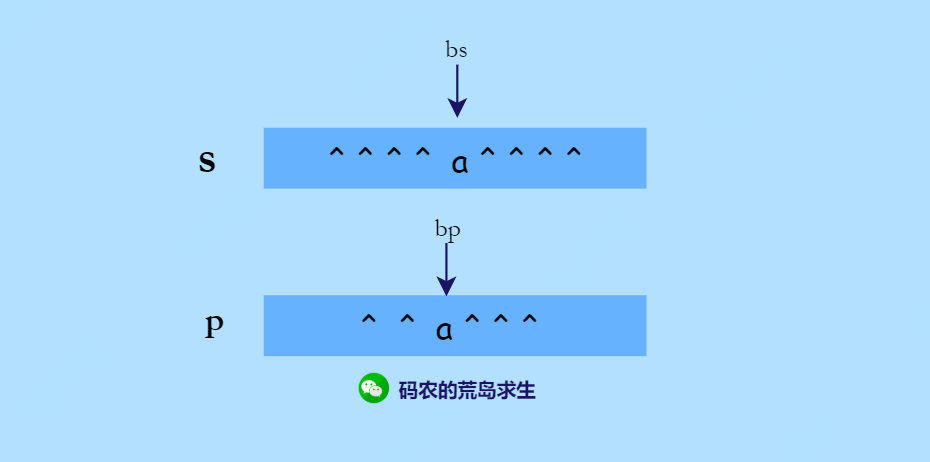
解释: '*'匹配0个或者多个前一个字符，也就是字符'a'. 因此重复一次就变成了"a".

在往下看之前先想一想该怎样解决这个问题，千万不要想得太复杂，用6行C++代码即可解决，我们先来分析一下。

从最简单的情况开始考虑。

如果给定的模式中没有星号"*"，那么问题再简单不过，可以使用递归函数轻松搞定（关于递归这个话题后续会有文章详细讲解）：

bool is_match(string& s, int bs, string&p, int bp) {
    if (bp == p.length()) return bs == s.length();
    bool is_first_match = (bs < s.length()) &&(s[bs] == p[bp] || p[bp] == '.');

    return is_first_match && is_match(s, bs+1, p, bp+1);
}

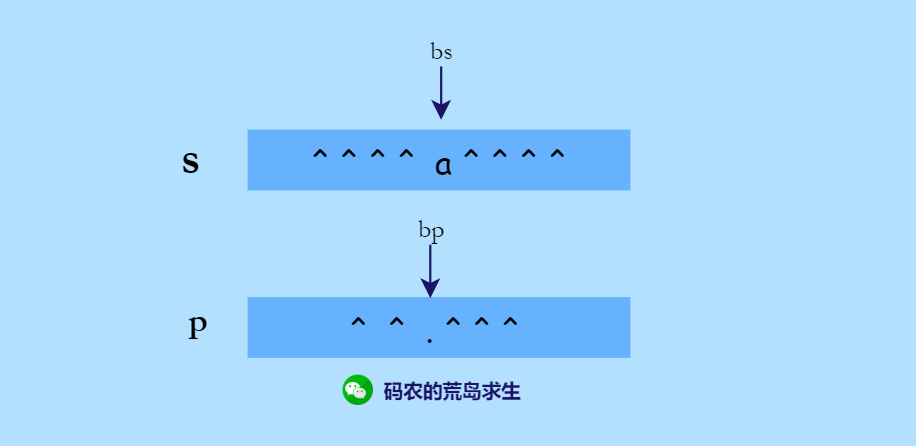
可以看到，真正的逻辑只有3行代码，其中参数bs、bp表示字符串s和模式p的起始下标，我们需要做的仅仅是判断当前字符s[bs]与模式中的字符p[bp]是否匹配，这分为两种情况：

1. 两个字符严格相同，（图中的^表示省略）

2. 模式中的当前字符为‘.’，因为‘.’可以匹配任意字符

这一部分的代码就一句话：

bool is_first_match = (bs < s.length()) &&(s[bs] == p[bp] || p[bp] == '.');

当前字符匹配后还要判断后面的子字符串是否也匹配：

is_match(s, bs+1, p, bp+1)

这样最简单的情况就考虑完毕。

接下来想要考虑星号，注意，这个题目最为关键是你必须意识到：

如果后一个字符是星号"*"，那么你需要将当前字符与星号“*”作为一个整体来考虑，而不能简单根据当前字符是否是星号来思考，再次强调，因为它们是一个整体

如果下一个字符为星号该怎么办呢？

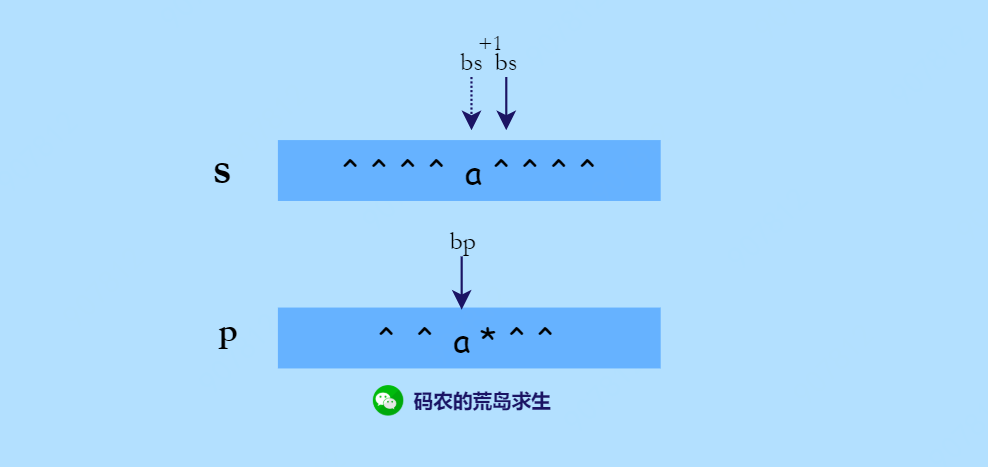
星号的作用有两个，一个是表示重复前一个字符0次，也就是说在这种情况下我们可以把当前字符与星号全部忽略掉，因此我们的bp可以直接往后移动2个位置去计算下一个子问题：

用代码表示就是：

is_match(s, bs, p, bp+2)

我们说过星号的作用有两个，一个是表示重复前一个字符0次；另一个是可以重复任意次，在后一种情况下就要求模式中的前一个字符必须和字符串中的当前字符匹配才可以，比如上图中字符串和模式中的字符都是a，因此我们可以重复使用“a*” 一次，这样bp指针无需移动只需要bs加1即可，表示重复使用一次：

用代码表示就是：

isfirstmatch && is_match(s, bs+1, p, bp);

这样完整的代码呼之欲出：

bool is_match(string& s, int bs, string&p, int bp) {
    if (bp == p.length()) return bs == s.length();
    bool isfirstmatch = (bs < s.length()) &&(s[bs] == p[bp] || p[bp] == '.');

    if (bp < p.length() - 1 && p[bp + 1] == '*') {
        return is_match(s, bs, p, bp+2) || isfirstmatch && is_match(s, bs+1, p, bp);
    } else {
        return isfirstmatch && is_match(s, bs+1, p, bp+1);
    }
}

可以看到，真正的逻辑只有6行，你就实现了一个正则表达式引擎。

仔细看上述代码，实际上该代码包含最优子结构（关于动态规划与最优子结构这个话题后续会有文章详细讲解），因此我们可以使用动态规划代码来解决。

动态规划

在动态规划版本中我们同样遵循一个原则，即：

如果后一个字符是星号"*"，那么你需要将当前字符与星号“*”作为一个整体来考虑，而不能简单根据当前字符是否是星号来思考，再次强调，因为它们是一个整体

我们规定：

dp[i][j] 表示文本0-i是否和模式0-j匹配

如果当前字符的下一个字符不是星号则：

dp[i][j] = (s[i] == p[j] || p[j] == '.') && dp[i-1][j-1];

而如果当前字符的下一个字符是星号那么：

dp[i][j] = dp[i][j-1] || ((s[i] == p[j]||p[j]=='.')&& dp[i-1][j]);

这样，递推表达式写出后剩下的就简单啦：

bool isMatchdp(string s, string p) {
    int lens = s.length();
    int lenp = p.length();

    s = "0" + s;
    p = "0" + p;

    vector<vector<bool>> dp(lens+1, vector<bool>(lenp+1, false));
    dp[0][0]=true;


    for (int j = 1; j <= lenp;j++) {
        if (j % 2 == 0 && p[j] == '*') {
            dp[0][j-1] = dp[0][j] = dp[0][j-2];
        }
    }

    for (int i = 1; i <= lens; i++) {
        for (int j = 1; j <= lenp; j++) {
            if (p[j] == '*') {
                dp[i][j] = dp[i][j-1];
            } else if (j != lenp && p[j+1] == '*') {
                dp[i][j] = dp[i][j-1] || ((s[i] == p[j]||p[j]=='.')&& dp[i-1][j]);
            } else {
                dp[i][j] = (s[i] == p[j] || p[j] == '.') && dp[i-1][j-1];
            }
        }
    }
    return dp[lens][lenp];
}

代码逐行详解

1， 可以看到代码中有这样两行定义：

s = "0" + s;
p = "0" + p;

这两行的作用是什么呢？

小风哥比较懒，在每个字符串前面加上“0”不会改变最终的结果，但是可以在接下来的循环中少一些corner case的判断，因为地推式中有这样的代码：

dp[i][j] = (s[i] == p[j] || p[j] == '.') && dp[i-1][j-1];

如果i或者j为0，那么减1后会变成负值，这显然会有问题

2， 有了1后定义dp数组时需要多定义1个

vector<vector<bool>> dp(lens+1, vector<bool>(lenp+1, false));

3， 同样因为1，我们知道dp[0][0]一定为true，因为“0”和“0”是匹配的。

4， 比较关键的是初始化部分的一段代码：

for (int j = 1; j <= lenp;j++) {
    if (j % 2 == 0 && p[j] == '*') {
        dp[0][j-1] = dp[0][j] = dp[0][j-2];
    }
}

假如给定的输入s是空字符串，而模式p不是：

s: 0
p: 0a*b*c*

我们知道dp(0,0)为true(“0”和"0"匹配)，dp(0,1)与dp(0,2)也应该为true，因为a*可以匹配空字符串，同理dp(0,3)与dp(0,4)的值也为true，因为b*也可以匹配空字符串，但dp(0,3)与dp(0,4)也要同时依赖dp(0,2)，因为如果是这样的输入：

s: 0
p: 0acb*c*

这时尽管b*同样可以匹配空字符串，但ac无法匹配空字符串，因此dp(0,3)与dp(0,4)的值为false

5， 剩下的for循环遵循之前给出的递推时，只需要注意一点：

如果后一个字符是星号"*"，那么你需要将当前字符与星号“*”作为一个整体来考虑，而不能简单根据当前字符是否是星号来思考，再次强调，因为它们是一个整体

因此如果当前字符的下一个字符是星号，那么dp(i,j)的值等于dp(i,j-1)即可：

for (...) {
    for (...) {
        if (p[j] == '*') {
           dp[i][j] = dp[i][j-1];
        } else ...
    }
}

怎么样，正则表达式还是不简单的吧，这里用了将近3000字来讲解，你学会了吗？