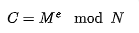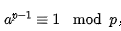一分钟了解 RSA 算法到底是个什么鬼？

背景

RSA 算法大家肯定都听说过了，它是一种常见的非对称加密算法，常用来对一些在网络上传输的敏感信息进行加密。

但具体流程不知道大家清楚不？本文将概述 RSA 算法的流程，并用一个简单示例进行阐述，最后讲解了一种意想不到的“旁门左道”的破解方式。

RSA 算法流程

具体算法流程如下：

1. 找到互质的两个数， p 和 q， 计算 N = p*q
2. 确定一个数 e， 使得 e 与 (p-1)(q-1) 互质， 此时公钥为 (N, e)， 告诉给对方
3. 确定私钥 d， 使得 e*d-1能够被(p-1)(q-1)整除
4. 消息传输方传输消息 M， 加密密文C为:
5. 消息接受方通过收到密文消息 C， 解密消息 M:

RSA算法依赖于欧拉定理，一个简化版本为大致为 a 和 p 互质，那么有:

即a 的 p-1 次方 对 p 取余为1，（a 的 p-1次方减去1可以整除 p）

欧拉定理的证明比较复杂，可以参考下文末的参考资料。

举个例子

还是用个简单示例来说明：

N = pq， 取俩素数 p=11, q = 3, N = p * q = 33， 取 e 与 (p-1)(q-1) = 20 互质的数 e = 3， 然后通过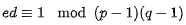 确定私钥， 即取一个 d 使得 3*d -1 能 20 被整除， 假设取 d=7 或者d=67。（3*7-1=20 当然能被20整除， 3*67-1=200 也能被20整除）

因此 public key 为 (N=33, e=3)， private key 为 d=7 或者d=67。

假设加密消息M=8， 通过加密算法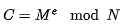 ，得到密文 C=8^3 % 33 = 17。

再来看解密， 由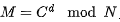 ，得到明文 M = 17^7 % 33 = 8 或者 M=17^67 % 33=8， 是不是很神奇? （这里^ 表示多少次方，后文中的有的表示异或）

来， 安利一个计算器的工具， bc 命令， 支持任意精度的计算， 其实 Mac简单的计算就可以通过前面介绍的 [Alfred] 可以方便得完成。

linux计算器

RSA 破解

如果需要破解 RSA 的话，就是需要找到 p 和 q， 使得 pq=33， 如果知道了 p 和 q 就能通过公钥 N 和 e 反推出私钥 d 了。

当然上面所述的案例较简单，当 N 很大时，就特别困难了。大数分解在历史以来就一直是数学上的难题。

曾经有人花了五个月时间分解了这个数39505874583265144526419767800614481996020776460304936454139376051579355626529450683609727842468219535093544305870490251995655335710209799226484977949442955603(159位数)， RSA-155 (512 bits) [from wikipedia]。

这条路走不通， 就有人走了"旁门左道"了， Stanford 的几个研究者用了两个小时破解了 OpenSSL 0.9.7 的 1024-bit 的 RSA 私钥 (感兴趣的同学可以看他们的论文Remote Timing Attacks are Practical)，用到的方法就是后面提到的时序攻击(或译为"计时攻击")。

计时攻击(Timing Attack)

计时攻击是边信道攻击(或称"侧信道攻击"，Side Channel Attack，简称 SCA) 的一种， 主要是一种利用不同的输入会有不同的执行时间这个特点进行的。

刚开始看到这个，我还是大为震惊的。凭直觉想，感觉要实际应用起来干扰项太多了，是不是可以直接忽略？

不过，看到上述论文有实际攻破成功的案例，以及各大编程语言纷纷补丁来看，这样做还是非常需要的，至少是“政治”正确的。

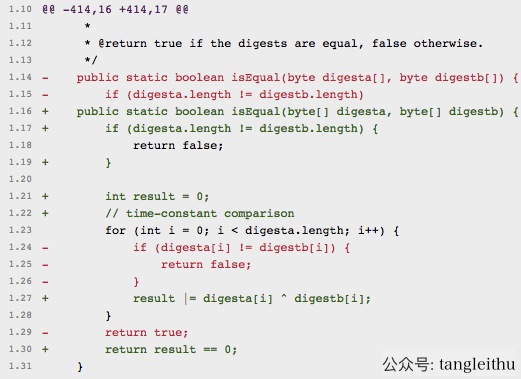
例如 JDK 1.6.0_17 中的Release Notes 中就提到了 MessageDigest.isEqual中的 bug 的修复，如下图所示：

MessageDigest.isEqual计时攻击

关于这个话题，更多内容可以参考我之前写的这篇文章 —— [这 10 行比较字符串相等的代码给我整懵了，不信你也来看看]

参考资料:

1. [Timing Attacks on RSA: Revealing Your Secrets through the Fourth Dimension](http://www.cs.sjsu.edu/faculty/stamp/students/article.html)
2. [Remote Timing Attacks are Practical](http://crypto.stanford.edu/~dabo/papers/ssl-timing.pdf)
3. [费马小定理](https://zh.wikipedia.org/wiki/%E8%B4%B9%E9%A9%AC%E5%B0%8F%E5%AE%9A%E7%90%86)

后记

以上内容若有不清楚或不正确的地方，还望大家指出，感谢。