贪心算法套路问题

最近在不间断、碎片的看贪心算法问题，相比回溯、动态规划问题，贪心算法理论最简单，死扣理论解决问题却很难，大部分的贪心问题一眼懵，很难看出是贪心问题，也很难找到解题套路，因此此部分介绍几道典型的贪心问题，并总结一套贪心套路帮助理解问题

贪心算法

算法策略

贪心算法，故名思义，总是做出当前的最优选择，即期望通过局部的最优选择获得整体的最优选择。

某种意义上说，贪心算法是很贪婪、很目光短浅的，它不从整体考虑，仅仅只关注当前的最大利益，所以说它做出的选择仅仅是某种意义上的局部最优，但是贪心算法在很多问题上还是能够拿到最优解或较优解，所以它的存在还是有意义的。

在日常生活中，我们使用到贪心算法的时候还是挺多的，例如：从100章面值不等的钞票中，抽出 10 张，怎样才能获得最多的价值？

我们只需要每次都选择剩下的钞票中最大的面值，最后一定拿到的就是最优解，这就是使用的贪心算法，并且最后得到了整体最优解。

往往遇到的问题并不是这么简单，例如：

二倍数对数组问题

给定一个长度为偶数的整数数组 arr，只有对 arr 进行重组后可以满足

• 对于每个 0 <= i < len(arr) / 2 ，都有 arr[2 * i + 1] = 2 * arr[2 * i] 时，返回 true；
• 否则，返回 false。

例如：

输入：arr = [4,-2,2,-4]
输出：true
解释：可以用 [-2,-4] 和 [2,4] 这两组组成 [-2,-4,2,4] 或是 [2,4,-2,-4]

解题思路：

[4,-2,2,-4] ，假设正数正向排序、负数逆向排序，得到 [-2,-4,2,4] ，那么遍历数组，每个数要不被之前的数匹配，要不之后存在 2 倍数

• 例如对于 arr[0]=-2 只能存在 2 倍数，不会存在 1/2 的数

也就是从 arr[0] 开始，仅仅只关注当前的 2倍数结果 ，仅仅关注当前局部的最优，通过每一步的最优解，获取全局最优解，这样看就是 贪心算法 问题

以上这样思路，称之为 抽象贪心算法模型

大部分的贪心问题，都很难看出来，我们最重要的是学会如何抽象成贪心算法模型，这步处理好，代码实现很简单

对于本题，我们还需要关注重复数的问题，例如 [2,2,4,4] ，可以使用 Set 去重，Map 记录重复个数，实现如下：

var canReorderDoubled = function(arr) {
  if(arr.length < 2) return false
  // 正数正序，负数逆序
  arr.sort((a, b)=>{
    if(a<0 && b<0) return b-a
    return a-b
  })
  // 去重
  let nums = [...new Set(arr)], map = new Map()
  // 记录重复数个数
  for(let a of arr) {
    map.set(a, (map.get(a) || 0)+1)
  }

  for(let i=0; i<nums.length; i++) {
    // 当前数与二倍数差值
    let temp = (map.get(nums[i] * 2) || 0)-map.get(nums[i])
    if(temp>=0) { // 满足当前二倍数，或已匹配
      map.set(nums[i] * 2, temp) // 只关注当前最优，局部最优
    } else {
      // 不满足
      return false
    }
  }
  return true
};

再看一道：

盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例：

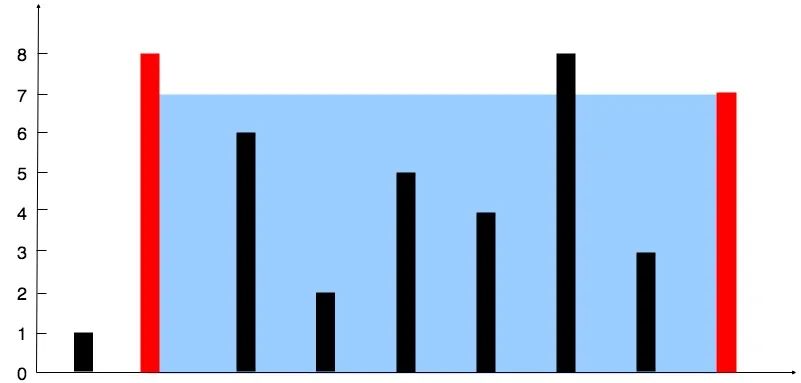
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

解题思路：

首先，两个边构成一个容器，这个容器的容水量由最短边和 x 轴间距决定，如果从 x 轴最大，即 i=0, j=height.length-1 开始选择两个边：

• 如果我们选择两个边的最长边，向内收缩一步，长边可能变得更长，但储水量只由短边和 x 轴间距决定，短边不变，x 轴间距缩小了，储水量只可能缩小
• 如果我们选择两个边的最短边，向内收缩一步，短边可能更长或缩小，如果更长的话，储水量可能会增加

因此，我们只要选择每次的局部最优：短边向内收缩一步，使用 res 更新每次操作后的全局最优，最终拿到整体最优，这就是 贪心算法 问题

以上这样思路，称之为 抽象贪心算法模型

代码实现：

var maxArea = function(height) {
  if(height.length <2) return 0
  let res = 0,
      i = 0,
      j = height.length-1
  while(i<j) {
    res = Math.max(Math.min(height[j],height[i])*(j-i), res)
    // 收缩
    if(height[i]<height[j]) {
      i++
    } else {
      j--
    }
  }
  return res
};

采用的是双指针解题，贪心算法是实现，双指针是实现手段，像回溯、动态规划都是思想，DFS、BFS是手段，所有的问题都离不开算法思想

相似的有：有效三角形的个数问题

贪心套路

第一步 判定是否是贪心问题

问题给出一组数据，并给出该组数据的条件或环境（限制），以及结果期望，要求判断这组数据是否满足期望，或从这组数据中选择部分数据，能否达到期望结果最优值

例如：

• 二倍数对数组问题：给出一组数据，限制数据重组后二倍数，判断所有的数据是否都满足二倍数关系
• 盛最多水的容器问题：给出一组数据 height ，限制每两个数都可以构成容器，求从这组数据中选择两个数据，达到容器最大值

第二步 抽象贪心算法模型

根据问题，抽象出符合满足局部最优，且能通过局部的最优选择获得整体的最优选择的贪心算法模型，例如：

• 二倍数对数组问题：数据正数正向排序、负数逆向排序后，每个数都向后满足二倍数关系，则整体都满足二倍数关系
• 盛最多水的容器问题：从 i=0, j=height.length-1 开始选择两个边，每次做出当前的最优选择：每次短边向内收缩一步，更新全局最优，最终拿到整体最优：容器最大值

贪心算法模型是对当前问题的一种抽象，一种变体，帮助我们解决问题， 不要问如何抽象贪心算法模型，多刷几道，刷着刷着就有感觉了

第三步 判断贪心解题是否最优

通过示例判断结果是否是最优解

经典案例：跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的 最大长度 。

判断你是否能够到达最后一个下标。

示例：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标

第一步 判定是否是贪心问题

给出一组数，限制每个数组代表能跳跃的最大长度，期待能够能够到达最后一个数字位置，贪心算法问题

第二步 抽象贪心算法模型

从下标 i=0 开始，选择当前局部最优，能够达到的最远位置 i+nums[i] ，然后和全局最优 end 对比，更新全局最优，最后拿到整体最优解

var canJump = function(nums) {
  // 全局最优
  let end = 0
  for(let i=0; i<nums.length; i++) {
    // 当前位置不可达，超出此前所有最大可达位置
    if(end < i) return false
    // 最大可达位置已经到达甚至超越最后一个下标，返回 true
    if(end >= nums.length-1) return true
    // 更新全局最优
    end = end > i+nums[i] ? end: i+nums[i]
  }
  return true
};

第三步 判断贪心解题是否最优

结合示例 [2,3,1,1,4] 验证结果正确

canJump([2,3,1,1,4]) // true

经典案例：跳跃游戏||

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

假设你总是可以到达数组的最后一个位置。

示例：

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

第一步 判定是否是贪心问题

给出一组数，限制每个数组代表能跳跃的最大长度，期待从中选择几个数字，能够最快（最少跳跃）到达最后一个数字位置，贪心算法问题

第二步 抽象贪心算法模型

从下标 i=0 开始，选择当前局部最优，能够达到的最远位置 end=i+nums[i] ，那么 i+1、...、end 为下一步跳跃可能的起点

从 i=i+1 继续遍历，选择当前局部最优，能够达到的最远位置 i+nums[i] ，然后和全局最远 maxPos 对比，更新全局最远，直到 i=end ，当前步起点跳跃结束，开启下一步，上一步全局最远 end 和全局最远 maxPos 对比，更新全局最远 end

这里 end 与 maxPos 不同：

• end 为上一步全局最优，上一步跳跃所能达到的最远位置，也是这一步起跳点的最远位置
• maxPos 为实时的全局最优，当启动新一轮跳跃时，为新一轮跳跃所能达到的最远位置

图片来自：https://leetcode-cn.com/problems/jump-game-ii/solution/45-by-ikaruga/

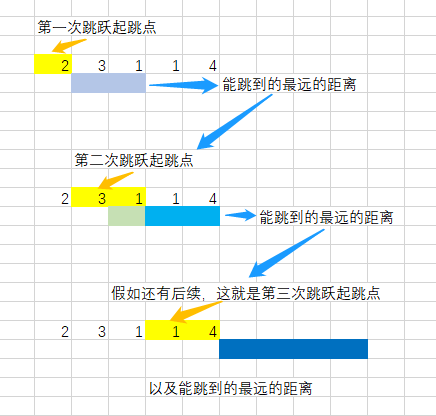
通过 end 选择每一轮的局部最优，更新跳跃次数，获取整体最优

var jump = function(nums) {
  let end = 0, 
      maxPos = 0,
      count = 0
  for(let i=0; i<nums.length-1; i++) {
    maxPos = maxPos >  i+nums[i] ? maxPos : i+nums[i]
    // 到达 count 轮终点，更新 end 与 count
    if(i === end) {
      // 启动下一轮
      end = maxPos
      // 更新跳跃次数
      count++
    }
  }
  return count
}

第三步 判断贪心解题是否最优

结合示例 [2,3,1,1,4] 验证结果正确

jump([2,3,1,1,4]) // 2

https://github.com/sisterAn/JavaScript-Algorithms/issues/171