贪心理论和常见的证明方法

Greedy Algorithm

贪心算法在每一步的选择中都会采取在当前状态下的最优决策，并希望由此产生的最终结果也是全局最优。

决策：局部最优（以希望能全局最优）

与一般的搜索（也称暴力搜索/蛮力搜索/枚举回溯）和动态规划相比，贪心算法的不同之处在于：它不对整个状态空间进行遍历或计算，而是始终按照局部最优的选择执行下去，不再回头。

搜索和动态规划会遍历整个状态空间。搜索有回溯，是蛮力遍历；动态规划是把状态分阶段+按顺序，然后选取代表+提炼最优子结构，从而更高效地处理所有状态。它两都是基于全局考量的，所以求解一定是对的。

正因为这个特性（不遍历整个状态空间），贪心算法不一定能得到正确的结果，除非可以证明。即证明：按照特定方法做出的局部最优选择，依然可以得到全局最优结果。

贪心，一定要证明。

引入贪心

举个例子，零钱兑换。

题目：给定一个整数数组 coins（表示不同面额的硬币）和一个整数 amount（表示总金额），计算并返回可以凑成总金额的最少硬币个数。如果没有任何一种硬币组合能组成总金额，就返回 -1。假设每种硬币的数量是无限的。

我们平时兑换零钱，是会尽量选择面额大的（因为这样可以更快地兑完）直到它不能兑换了为止，然后剩余的再用小面额的凑齐（策略一致）。

“每次都选尽量大的面值”就是一个贪心思想。

那我们思考，它对吗？不一定对。

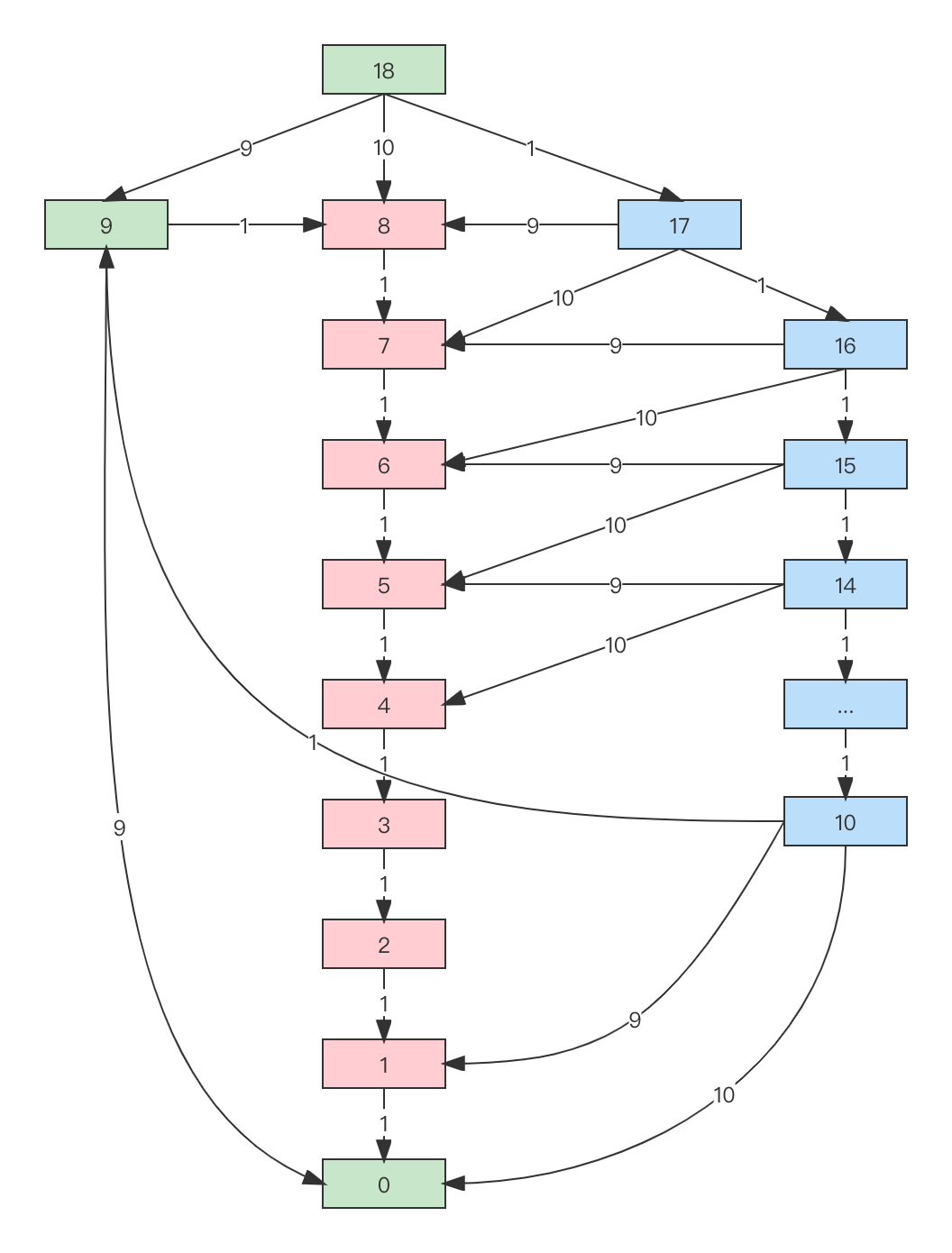
比如用 [10,9,1] 兑换 18（状态图如下），如果用贪心策略兑换，就会走图中的红色路径，即需要 9 个硬币（1 个 10 和 8 个 1），而最优解是绿色路径，即需要 2 个硬币（2 个 9）。

如果是暴力搜索，它会遍历所有状态 [剩余金额, 已用硬币数]，然后取最小的硬币数。虽然搜索也会考虑贪心选的那条路径，但它会遍历所有边所有点。

贪心算法不一定能得到正确的解，在大部分题目上不能随便使用。如果要使用贪心算法，就必须先证明它的正确性。

三种证明方法

除了数学归纳法和反证法之外，还有三种常用的证明方法。

1. 决策包容性

决策包容性是从“状态空间”这一本质出发的一个证明方法。包容，即包含，指子集包含。子集，是可达边界构成的子集。

贪心算法实际上是在状态空间中按照局部最优策略找了一条路径。如果我们能证明：从一个点出发，它还能到达最优解，即并不会丢失最优解的可达性。那么，这样的贪心就是对的。

比如用 [5,10,20] 来兑换零钱，贪心算法是成立的，因为它们的面值互成倍数，此时能用 1 张 10 块兑换的必然也能用 2 张 5 块的来兑换。在这种情况下，“每次都选尽量大的面值”的局部最优策略是有包容性的。

再来看两个例子。

题目1：柠檬水找零。每杯柠檬水售价为 5，给定一个整数数组 bills，bills[i] 里存着第 i 位顾客付的账，值只会是 5、10、20，判断能否给每位顾客正确找零。注意：一开始手头并没有任何零钱。

代码如下：

var lemonadeChange = function(bills) {
  const moneys = {
    5: 0,
    10: 0,
    20: 0
  };

  // 找零：用贪心策略 “在可选的面额里取最大的”
  const exchange = function(amount) {
    for (let x of [20, 10, 5]) {
      // 用循环减法替代除法和%
      while (amount && x <= amount && moneys[x] > 0) {
        amount -= x;
        moneys[x]--;
      }
    }
    return amount === 0;
  };

  // 遍历账单
  for (let x of bills) {
    if (!exchange(x - 5)) return false;
    moneys[x]++;
  }
  return true;
};

题目2：分发饼干。给定一个孩子的胃口数组 g 和一个饼干的尺寸数组 s，求能满足最多孩子的个数。孩子 i 的胃口值 g[i]，饼干 j 的尺寸值 s[j]，如果 s[j] >= g[i]，那就可以将这个饼干 j 分配给孩子 i ，此时孩子 i 会得到满足。

代码如下：

var findContentChildren = function(g, s) {
  // 原地排序：小-大
  g.sort((a, b) => a - b);
  s.sort((a, b) => a - b);

  let ans = 0;
  let j = 0, sn = s.length;
  // 贪心策略：对于孩子 child，选择一个能满足其胃口的“最小”饼干
  for (let child of g) {
    while (j < sn && child > s[j]) j++;
    if (j >= sn) break;
    ans++;
    j++;
  }
  return ans;
};

以上两个例子，能都用决策包容性来证明贪心理论的正确性，所以可以用贪心算法求解。

决策包容性，只看一条边。

2. 扩展决策范围

在思考贪心算法时，有时候不容易直接证明局部最优决策的正确性，此时可以往后多扩展一步，进而对当前的决策进行验证。扩展决策范围，即往后多看一步。

决策扩展范围，是看两条边。

来看两个例子。

题目1：跳跃游戏。给定一个非负整数数组 nums，其中 nums[i] 表示在该位置可以跳跃的最大长度。起初是位于数组的第一个位置，求跳到数组最后一个位置的最少跳跃次数。

代码如下：

var jump = function(nums) {
  // 目的地：最后一个位置的下标
  let target = nums.length - 1;

  let ans = 0;
  let cur = 0;
  while (cur < target) {
    let jumping = cur + nums[cur];
    // 如果本位置跳一下就能到达目的地，则直接返回+1
    if (jumping >= target) return ans+1;
    // 否则，判断下一步跳哪里
    // 贪心策略：在当前位置的可跳范围内，选一个能跳“最远”的那个位置
    let farest = -1;
    let next = -1; // 下个位置
    for (let j = cur + 1; j <= jumping; j++) {
      if (j + nums[j] > farest) {
        farest = j + nums[j];
        next = j;
      }
    }
    // 卡这里了，走不动了，也到不了目的地了
    if (next === -1) return -1;
    // 否则，跳至下个位置，步数+1
    cur = next;
    ans++;
  }
  return ans;
};

题目2：买卖股票的最佳时机。给定一个数组 prices，其中 prices[i] 表示股票第 i 天的价格，求能获得的最大利润。说明：任何时候最多只能持有一股股票，在每一天中可以购买或出售，不限交易次数。

代码如下：

var maxProfit = function(prices) {
  let ans = 0;
  for (let i = 0; i < prices.length - 1; i++){
    // 贪心策略：如果明天涨，那就买入（以此获得所有上涨区间的全部收益）呃~预言家式炒股
    ans += Math.max(prices[i + 1] - prices[i], 0);
  }
  return ans;
};

以上两个例子，都能用“扩展决策范围+决策包容性”来证明贪心理论的正确性，所以可以用贪心算法求解。

3. 邻项交换

多用于求顺序的题目，即按照某个顺序来完成一个任务。贪心理论认为按照某个顺序排列是比较优的，此时要证明它，就可以用邻项交换法。

证明：无论什么情况下，只要沿着逆序方向走，就会让答案变差。

这样就能证明按有序的方向走，必然能得到最优解。贪心算法的实现就是碰到逆序的就给它局部邻项交换下，此时得到的序列就是最优序列。

至于“逆序/有序”的定义，就得看具体场景了。举个例子。

题目1：完成所有任务的最少初始能量。给定一个任务数组 tasks，tasks[i] = [actuali, minimumi]，其中，第一个元素表示完成第 i 个任务需要耗费的实际能量，第二个元素表示开始第 i 个任务前需要达到的最低能量。求完成所有任务的最少初始能量。

代码如下：

var minimumEffort = function(tasks) {
  // 贪心策略：按元素的 actual - minimum 升序排列，以此顺序完成任务
  tasks.sort((a, b) => a[0] - a[1] - (b[0] - b[1]));
  // 倒着计算初始能量
  let ans = 0;
  for (let i = tasks.length - 1; i >= 0; i--) {
    ans = Math.max(ans + tasks[i][0], tasks[i][1]);
  }
  return ans;
};

总结

贪心算法在每一步的决策中都采取局部最优策略，并希望由此导致的最终结果也是全局最优的。它不会遍历整个状态空间，因此贪心算法不一定能得到正确的结果，除非可以证明。

如果要使用贪心算法，就必须先证明它的正确性。除去熟知的数学归纳法和反证法之外，还有三种重要的证明方法，分别是决策包容性、扩展决策范围和邻项交换法。它们也可以结合使用，以证明做什么决策是最好的。

写在最后

搜索、动态规划和贪心是一脉相承的，都基于状态。不同之处在于搜索和动态规划会遍历整个状态空间，而贪心不会。正因为如此，贪心算法得到的结果不一定正确（除非可以证明），而基于全局状态的算法求出的最优解一定是正确的。

用贪心能做的题目，一般也都可以用搜索或者动态规划来求解，只是贪心一般是最高效的。所以，遇到问题，先想想搜索和动态规划，先对整体的状态空间有个了解。如果时间复杂度太高或是运行太慢，再考虑贪心（此时，也可能会更容易一些）。搜索→动态规划→贪心，是一个比较好的思路。

还是要格外强调：任何时候做题不要先想贪心。因为在不考虑时间复杂度的情况下，用搜索和动态规划总是可以求解的。同时，贪心一定要证明。

主要参考

• https://u.geekbang.org/lesson/270?article=430096