上周发了篇文章，关于[一名 95 后女程序员（4 年前端开发）] ，对现状的担忧与对未来的焦虑担忧，文章一经发出，后台就收到很多反馈，大部分的人都表示认同：

因此，我决定把自己的每日进阶记录下来，有时可能 2-3 天一起，每日内容不多，如果你不清楚怎么做，就和我一起吧，如果你有规划，也可以关注「三分钟学前端」，添加我的微信 pzijun_com，将你的每日进阶记录发送到群群里，我们一起督促学习

回溯算法

什么是回溯算法问题？

回溯算法是一种搜索法，试探法，它会在每一步做出选择，一旦发现这个选择无法得到期望结果，就回溯回去，重新做出选择。它就是不断的尝试，直到拿到解。因此它类似于一种暴力穷举的算法，此类问题一般都很少考虑时间复杂度问题

它的这种算法思想，使它通常用于解决广度的搜索问题，即从一组可能的解中，选择一个满足要求的解，或得到所有满足要求的解。因此它常采用深度优先遍历（DFS）求解

我们最常遇到的问题，例如：

• 全排列问题
• 括号生成问题
• 组合总和问题
• 树的深度遍历问题

全排列问题

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

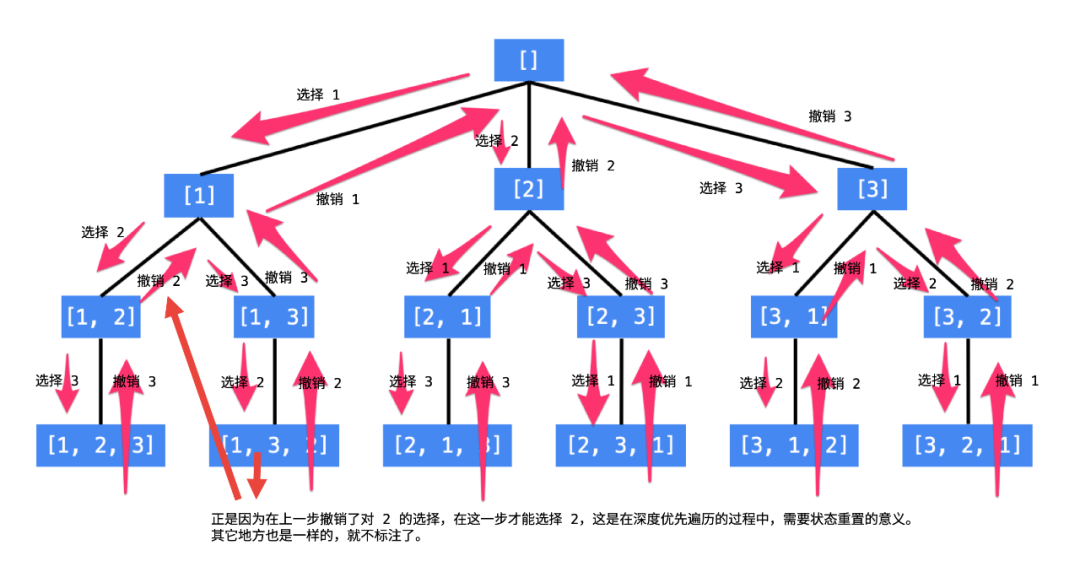
它的核心思路就是类似一个多叉树的形式，我们把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走。

图片来自于：https://pic.leetcode-cn.com/0bf18f9b86a2542d1f6aa8db6cc45475fce5aa329a07ca02a9357c2ead81eec1-image.png

let permute = function(nums) {
    // 使用一个数组保存所有可能的全排列
    let res = []
    if (nums.length === 0) {
        return res
    }
    let used = {}, path = []
    dfs(nums, nums.length, 0, path, used, res)
    return res
}
let dfs = function(nums, len, depth, path, used, res) {
    // 所有数都填完了
    if (depth === len) {
        res.push([...path])
        return
    }
    for (let i = 0; i < len; i++) {
        if (!used[i]) {
            // 动态维护数组
            path.push(nums[i])
            used[i] = true
            // 继续递归填下一个数
            dfs(nums, len, depth + 1, path, used, res)
            // 撤销操作
            used[i] = false
            path.pop()
        }

    }
}

括号生成问题

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例：

输入：n = 3
输出：[
       "((()))",
       "(()())",
       "(())()",
       "()(())",
       "()()()"
     ]

对应于本题，最开始是 ''，我们可以每次试探增加 ( 或 ) ，注意：

• 加入 ( 的条件是，当前是否还有 ( 可以选择
• 加入 ) 的时候，受到 ( 的限制，如果已选择的结果里的 ( 小于等于已选择里的 ) 时，此时是不能选择 ) 的，例如如果当前是 () ，继续选择 ) 就是 ()) ，是不合法的

代码实现：

const generateParenthesis = (n) => {
    const res = []
    const dfs = (path, left, right) => {
        // 肯定不合法，提前结束
        if (left > n || left < right) return
        // 到达结束条件
        if (left + right === 2 * n) {
            res.push(path)
            return
        }
        // 选择
        dfs(path + '(', left + 1, right)
        dfs(path + ')', left, right + 1)
    }
    dfs('', 0, 0)
    return res
}

组合总和问题

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

• candidates 中的 同一个 数字可以无限制重复被选取 。
• 如果至少一个数字的被选数量不同，则两种组合是不同的。

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

对应于本题，从 candidates 选择数，每个数可以选择多次，使用 index 记录当前选到第几个数，不可向前选择，防止重复，count 为当前满足条件的 index 位的数最多可选 count 次，由 0 ... count 次往后递归

• paths：已选数
• sum：已选数和
• index：当前选到第几个数

var combinationSum = function(candidates, target) {
    let res = [], map = new Map()
    let dfs = function(paths, sum, index) {
        if(sum > target || index > candidates.length) return
        if(target === sum) {
            res.push(paths)
            return 
        }
        // 计算当前数可选的倍数
        let count = Math.floor((target-sum)/candidates[index])
        // 选择当前数
        for(let i = 0; i <= count; i++) {
            dfs(new Array(i).fill(candidates[index]).concat(paths), sum+i*candidates[index], index+1)
        }
    }
    dfs([], 0, 0)
    return res
};

优化：

var combinationSum = function(candidates, target) {
    let res = [], map = new Map()
    let dfs = function(paths, sum, index) {
        if(sum > target || index > candidates.length) return
        if(target === sum) {
            res.push(paths)
            return 
        }
        dfs(paths, sum, index+1)
        if(target-sum>=candidates[index]) {
          dfs([...paths, candidates[index]], sum+candidates[index], index)
        }
    }
    dfs([], 0, 0)
    return res
};