递归的本质及其基本实现形式

recursion, 递归

递归和递推都是程序的一种基本实现形式，它们可以用来实现一系列算法，比如搜索/分治/树的遍历/深搜等。

如何理解递归？

我们知道，递推可以通过 for 循环来重复一个从小到大的过程，比如前缀和的递推公式 S[i] = S[i-1] + A[i]、阶乘的递推公式 f(n) = n * f(n-1)。

eg1. 用 for 循环实现阶乘

// 用 for 循环实现阶乘
function factorial(n) {
    let ans = 1;
    for (let i = 1; i <= n; i++) ans *= i; // 递推公式 f(n) = f(n-1) * n
    return ans;
}
console.log(factorial(6)); // 720

递归，本质上也是重复，只是它不是基于循环语句，而是基于函数。我们通过用函数自己调自己的方式，来实现一个以函数体进行循环的运算，函数体的每层是自相似的（参数不同）。递归的本质就是把函数体作为一个重复（循环）的过程。

eg2. 用递归实现阶乘

// 函数自己调自己，以实现循环
function factorial(n) {
    if (n === 1) return 1;
    return n * factorial(n - 1); // 递推公式 f(n) = n * f(n-1)
}
console.log(factorial(6)); // 720

循环的不同实现方式

为了更直观地了解 for 循环和递归循环这两种执行过程之间的异同，我们对上面的两个代码加上 log，输出见代码底部的注释。

eg1. 用 for 循环实现阶乘

// 用 for 循环来实现阶乘 n!
function factorial(n) {
    let ans = 1;
    for (let i = 1; i <= n; i++) {
        ans *= i;
        console.log(`for *${i} = ${ans}`); // 打 log 方便查看“循环过程”
    }
    return ans;
}
console.log(factorial(6)); // 720 = 6*5*4*3*2*1
// for *1 = 1
// for *2 = 2
// for *3 = 6
// for *4 = 24
// for *5 = 120
// for *6 = 720

eg2. 用递归实现阶乘

function factorial(n) {
    console.log(`factorial(${n})`);
    if (n === 1) {
        console.log('\t返回计算结果：1');
        return 1;
    }
    let recurAns = factorial(n - 1);
    let ans = n * recurAns;
    console.log(`\t返回计算结果：${ans} = ${n} * ${recurAns}(~${n - 1}...1)`);
    return ans;
}
factorial(6);
// factorial(6)
// factorial(5)
// factorial(4)
// factorial(3)
// factorial(2)
// factorial(1)
//     返回计算结果：1
//     返回计算结果：2 = 2 * 1(~1..1)
//     返回计算结果：6 = 3 * 2(~2..1)
//     返回计算结果：24 = 4 * 6(~3..1)
//     返回计算结果：120 = 5 * 24(~4..1)
//     返回计算结果：720 = 6 * 120(~5..1)

通过对比，我们可以看出：for 循环是直接从小到大进行递推的，而递归是先往下层层探下去，再向上层层推上来（递推）。递归多了一个“往下探”的过程，如下图所示：

虽然乍看会觉得递归反而更繁琐了，但是对于某些推导路径不那么直观的问题来说，递归的这种实现方式还是更直观些的，比如用分治的思想合并 k 个有序链表、计算 x 的 n 次方，比如和树/图相关的问题。

此时，如果要将递归展开成 for 循环，可重点关注递归下探到底之后，再“层层向上递推”的那部分逻辑。

这里我们就重点理解，递归是如何利用函数本身来实现循环的。

基本实现形式

结合递归的本质，我们再来看看它的实现形式。

三个关键

首先，需要明确要递归的问题，即定义重叠/相似的子问题（数学归纳法的思维）。

其次，为了保证程序可以正常停止，需要确定递归边界。有时是需要在叶子结点处显式地写 return 语句，有时是不需要的（因为此时递归树本身的生长是有边界的）。

第三点就是保护与还原现场。对于需要维护全局变量（状态空间）的情况，当每次一层一层向上推的时候（回溯）都要还原现场，以防不同分支间相互影响。对于有些情况，是不需要考虑这点的（因为没有全局变量）。

1. 函数体 + 传参调自己：循环的主体，即相似子问题
2. 递归边界：防止死循环
3. 还原现场：如果之前改了一些值的话

三种基本模板

递归的三种基本模板，分别是子集、组合和排列，对它们进行各种变形和组合就能扩展出各种各样的递归问题。

子集

题目：给定一个整数数组 nums（元素各不相同），返回该数组所有可能的子集（幂集）。

思路：依次判定每个元素选还是不选。比如 [1,2,3]，递归树如下：

var subsets = function(nums) {
    const n = nums.length;
    let ans = [];

    // 递归
    let sub = []; // 子集列表（共享变量）
    const recur = function(i){
        if(i===n) {
            ans.push([...sub]); // 浅拷贝
            return;
        }
        // 不选择当前元素
        recur(i+1);

        // 选择当前元素
        sub.push(nums[i]);
        recur(i+1);
        sub.pop(); // 还原现场
    };

    // 从第0个元素开始
    recur(0);
    return ans;
};

给代码加上 log，以 [1,2,3] 为例，其执行过程如下图所示（和上面画的递归树是一一对应的）：

打日志的代码就不单独放了，有些繁琐。原计划把 log 的代码也放在上面的示例上，但是太丑了，可读性不好，还影响对主逻辑的理解。感兴趣的朋友可以自己边 run 边 log。

组合

题目：给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

思路：和子集的一样，只是多了一个长度限制。有一个小技巧就是剪枝，它可以更早地发现不合法的情况，以便尽早退出，以此来提高搜索效率。

var combine = function (n, k) {
    const ans = [];
    const sub = []; // 子集（共享变量-状态空间）
    const recur = function (i) {
        // 剪枝1：长度>k了
        // 剪枝2：即便后面的都选上，也不可能成为答案（提前下探）
        if (sub.length > k || sub.length + (n - i + 1) < k) return;
        // 此时到达叶子结点的，就是答案了，长度=k
        if (i > n) {
            ans.push([...sub]);
            return;
        }
        // 每层的相似逻辑：i不选或者选
        recur(i + 1);

        sub.push(i);
        recur(i + 1);
        sub.pop(); // 恢复现场
    };
    recur(1);
    return ans;
};

排列

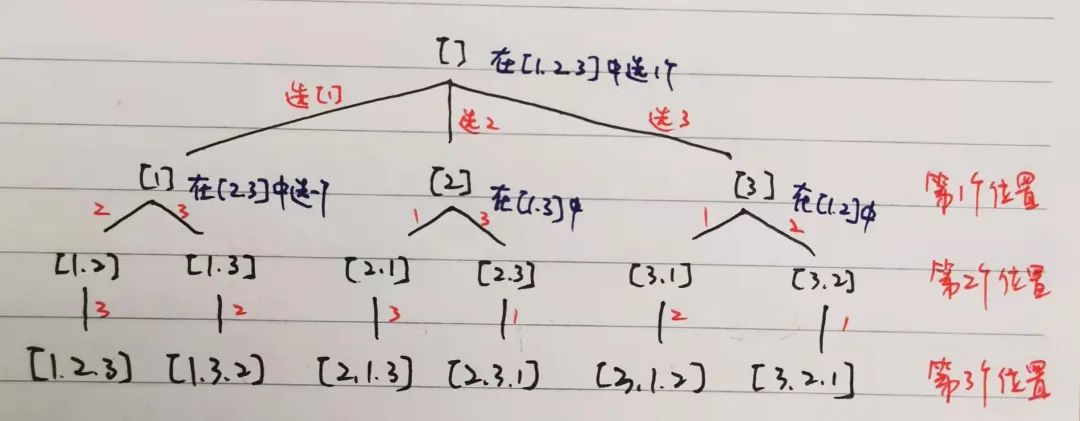
题目：给定一个不含重复数字的数组 nums，返回其所有可能的全排列。

思路：一共有 n 个位置，考虑每个位置放哪个数字，从还没有选过的数里选一个。

var permute = function (nums) {
    const n = nums.length;
    const ans = [];

    // 共享变量（状态空间）
    let used = []; // 已经被选过了的元素下标
    let permutation = []; // 排列

    // 递归：在第i个位置放一个数
    const recur = function (i) {
        if (i === n) {
            ans.push([...permutation]);
            return;
        }
        // N叉树，确保[0,n-1]上的元素都有可能出现在位置i上
        for (let j = 0; j < n; j++) {
            if (!used[j]) {
                permutation.push(nums[j]);
                used[j] = true;
                recur(i + 1);
                used[j] = false; // 恢复现场
                permutation.pop();
            }
        }
    }
    recur(0);
    return ans;
};

小结

以上三个问题都是用递归实现的暴力搜索（或者枚举回溯），它们都是去尝试试探每一个分支，然后推导出所有路径。

子集的思想是对于每个数决定选还是不选（子问题）。然后再一个一个来，直到把数组全部扫完（重复），它是个指数型的问题。

组合是从元素里选定 k 个，它依然是选数，只是限制了个数。在具体实现上，可以通过剪枝来提高搜索效率。

全排列的思想是考虑每个位置放哪个数（子问题）。第一个位置有 n 种选法，第二位置有 n-1 种选法，以此类推（重复），它是个 n 阶乘的问题。全排列的方案数是 n!。

当然，递归并不局限于这三种形式，但它们是最基础最经典的，与之对应的还有很多类似的系列问题。子集对应一系列时间复杂度是指数的问题，比如大体积背包。有些问题可以抽象成全排列的问题，比如 N 皇后；找顺序的都是全排列的问题，比如旅行商。组合型问题就是在一个集合里选一部分。

递归形式	时间复杂度规模	问题举例
指数型	kn	子集、大体积背包
排列型	n!	全排列、旅行商、N 皇后
组合型	n! / m!(n-m)!	组合选数

总结

递归的本质是重复，只是它不是基于循环语句，而是基于函数。与熟悉的 for 循环相比，递归多了一个先往下层层下探的过程，即先向下探寻、再向上递推。

递归的三个关键是明确递归问题、确定递归边界、保护与还原现场。虽然并不是所有的递归问题都同时具有这三个要素，但还是非常鼓励大家在每次写完一个递归代码的时候，都有意识地确认下这三个关键点，看看它们是如何在递归代码中扮演自己的重要角色的，以此积累解决问题的通识。

主要参考

https://u.geekbang.org/lesson/270?article=421259