【零基础】充分理解WebGL(二)
接上一篇:[【零基础】充分理解WebGL(一)]
在继续深入之前,我们先来解决上一篇中的遗留问题:
我们默认不设置顶点的时候,绘制的图形是整个 canvas 范围,但是 WebGL 并不支持四边形图元,那么我们原本的绘制范围是如何界定的呢?
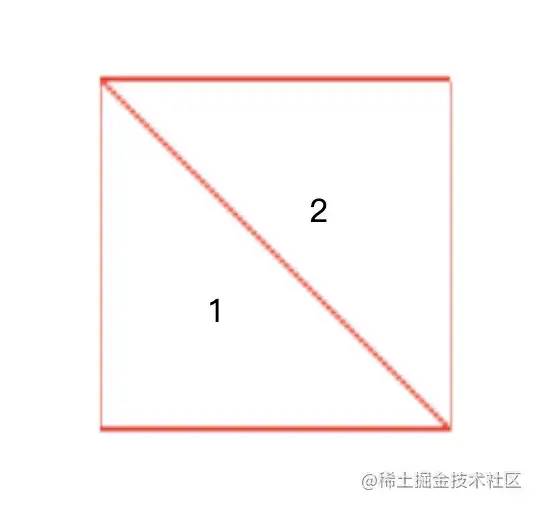
因为三角形是基本图元,而 Canvas 画布本身是一个四边形,所以我们需要使用两个三角形的顶点进行绘制,这也是 gl-renderer 默认的顶点数据,它相当于:
renderer.setMeshData([
{
positions: [[-1, -1, 0], [1, -1, 0], [1, 1, 0], [-1, 1, 0]],
cells: [[0, 1, 3], [3, 1, 2]],
},
]);如下图所示,我们用两个三角形来完成四边形的绘制。
用 WebGL 绘制平面图形,三角剖分是一种基本的方法。不过这个问题我们可以留待后续的文章详细讲解。在这一讲我们先回到片段着色器部分,来谈谈利用着色器或者说利用 GPU 进行造型绘图的基本原理和方法。
与上一讲一样,我们通过动手代码实践来理解,先从简单的开始。
最简单的单色绘制,在上一讲已经说过了,比如下面的代码,将整个绘图区绘制为黑色:
const canvas = document.querySelector('canvas');
const renderer = new GlRenderer(canvas, {webgl2: true});
const fragment = `#version 300 es
precision highp float;
out vec4 FragColor;
void main() {
FragColor = vec4(0, 0, 0, 1);
}
`;
const program = renderer.compileSync(fragment);
renderer.useProgram(program);
renderer.render();下面我们稍微修改一下代码:
const canvas = document.querySelector('canvas');
const renderer = new GlRenderer(canvas, {webgl2: true});
const fragment = `#version 300 es
precision highp float;
out vec4 FragColor;
uniform vec2 resolution;
void main() {
vec2 st = gl_FragCoord.xy / resolution;
FragColor = vec4(0, 0, 0, 1);
if(st.x > 0.5) {
FragColor = vec4(1, 1, 1, 1);
}
}
`;
const program = renderer.compileSync(fragment);
renderer.useProgram(program);
renderer.uniforms.resolution = [canvas.width, canvas.height];
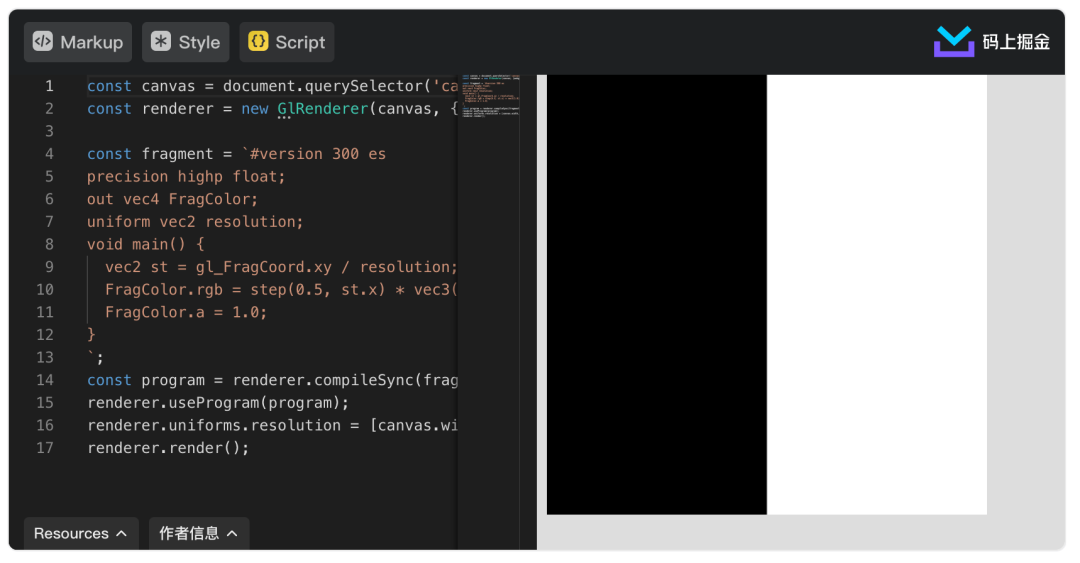
renderer.render();上面的代码很好理解,我们判断 x 坐标大于 0.5 时,输出颜色白色,否则为黑色。这样我们得到如下的效果:

if(st.x > 0.5)来判断黑白分界线,实际上我们有更简单的办法:
#version 300 es
precision highp float;
out vec4 FragColor;
uniform vec2 resolution;
void main() {
vec2 st = gl_FragCoord.xy / resolution;
FragColor.rgb = step(0.5, st.x) * vec3(1.0);
FragColor.a = 1.0;
}https://code.juejin.cn/pen/7100850170283163656
step函数来代替if语句,step(x, y)是阶梯函数,当 y 小于 x 时值为 0,y 大于等于 x 时值为 1。
在着色器中,step是一个非常好用的函数,可以使用它来绘制不同的图形。
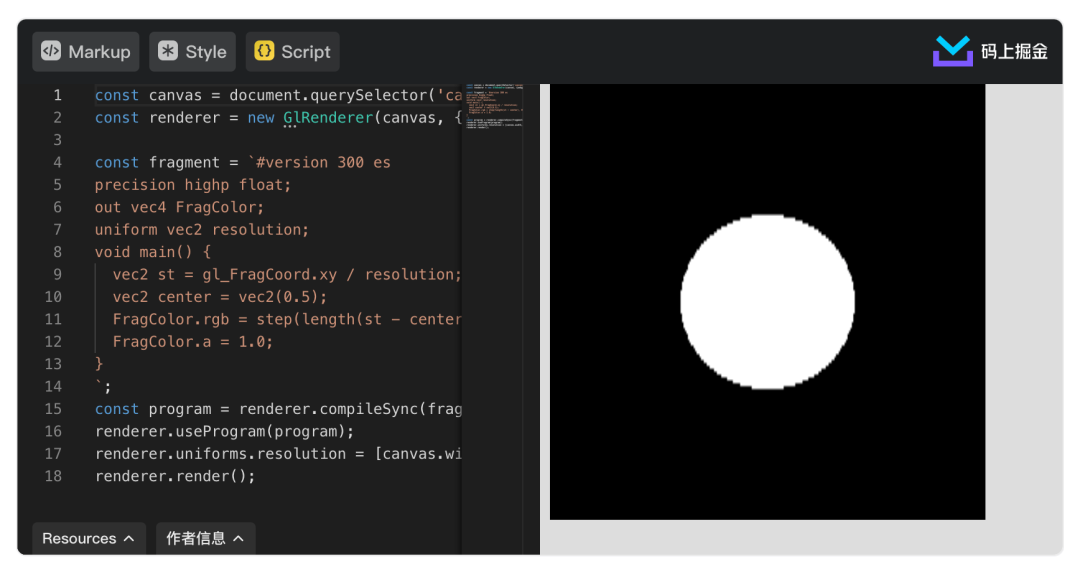
比如下面这个例子通过step绘制一个圆形:
#version 300 es
precision highp float;
out vec4 FragColor;
uniform vec2 resolution;
void main() {
vec2 st = gl_FragCoord.xy / resolution;
vec2 center = vec2(0.5);
FragColor.rgb = step(length(st - center), 0.2) * vec3(1.0);
FragColor.a = 1.0;
}https://code.juejin.cn/pen/7100852428756484103
消锯齿
直接用step绘制曲线,容易产生锯齿,我们可以通过smoothstep来消除锯齿:
#version 300 es
precision highp float;
out vec4 FragColor;
uniform vec2 resolution;
void main() {
vec2 st = gl_FragCoord.xy / resolution;
vec2 center = vec2(0.5);
float d = length(st - center);
FragColor.rgb = smoothstep(d - 0.015, d, 0.2) * vec3(1.0);
FragColor.a = 1.0;
}https://code.juejin.cn/pen/7100853943923638280
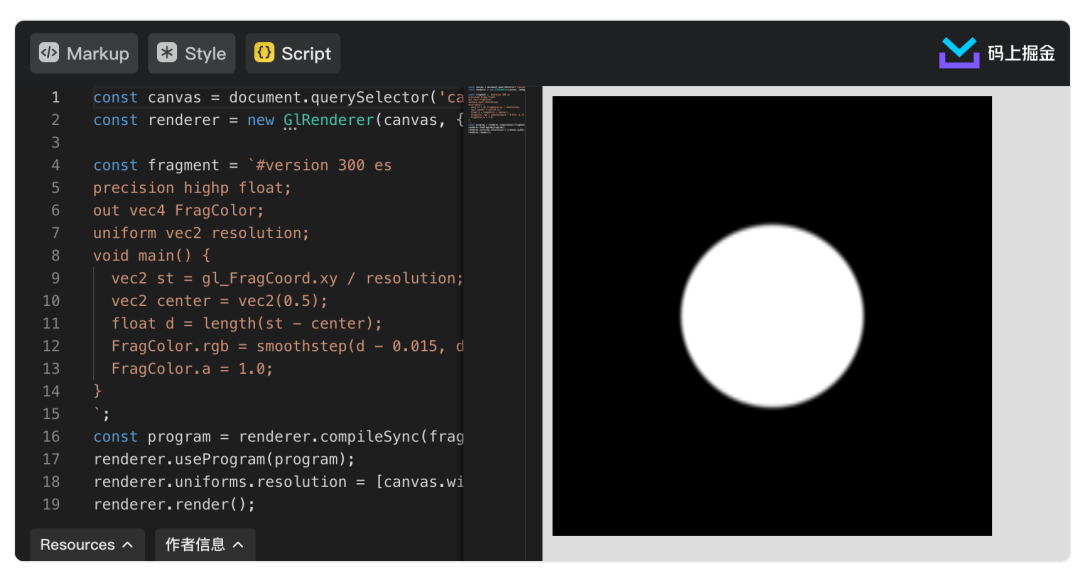
smoothstep 对阶梯函数进行了平滑处理,它在范围的上下限之间进行插值。
通过两个 step 相减或者两个 smoothstep 相减的技巧,可以用来画线,例如我们修改一下上面的代码:
#version 300 es
precision highp float;
out vec4 FragColor;
uniform vec2 resolution;
void main() {
vec2 st = gl_FragCoord.xy / resolution;
vec2 center = vec2(0.5);
float d = length(st - center);
FragColor.rgb = (smoothstep(d - 0.015, d, 0.2) - smoothstep(d, d + 0.015, 0.18)) * vec3(1.0);
FragColor.a = 1.0;
}就可以绘制一个圆环:
float stroke(float d, float d0, float w, float smth) {
float th = 0.5 * w;
smth = smth * w;
float start = d0 - th;
float end = d0 + th;
return smoothstep(start, start + smth, d) - smoothstep(end - smth, end, d);
}它的第一个参数接受一个距离量,第二个参数在指定距离的等距线附近绘制,第三个参数表示绘制宽度,第四个参数是平滑比率。
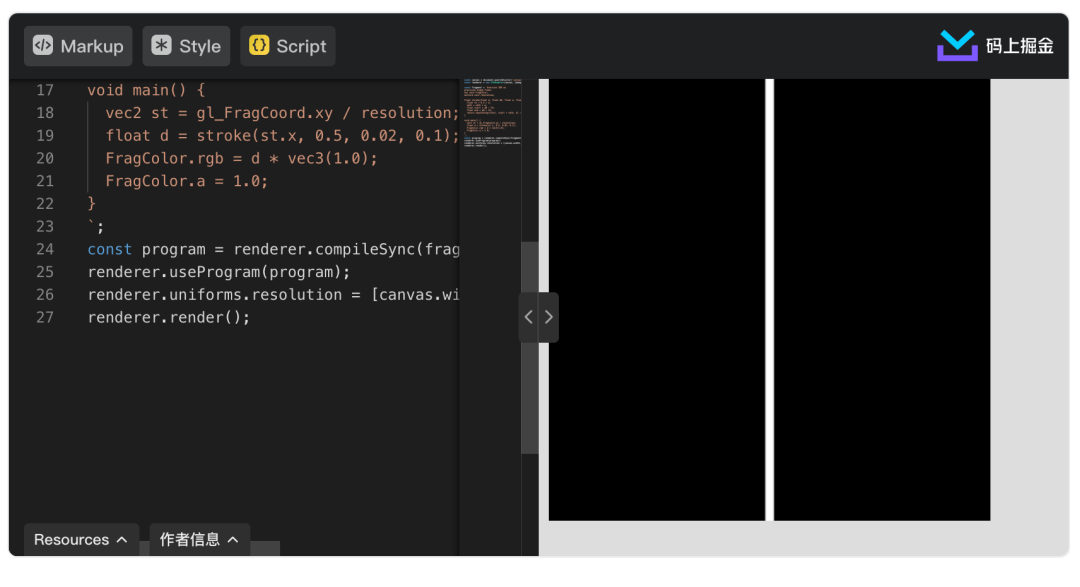
这样我们就可以用stroke来画线了,只要我们能把距离定义出来,比如下面的代码绘制了一条 x=0.5 的直线:
void main() {
vec2 st = gl_FragCoord.xy / resolution;
float d = stroke(st.x, 0.5, 0.02, 0.1);
FragColor.rgb = d * vec3(1.0);
FragColor.a = 1.0;
}https://code.juejin.cn/pen/7100857056361447454
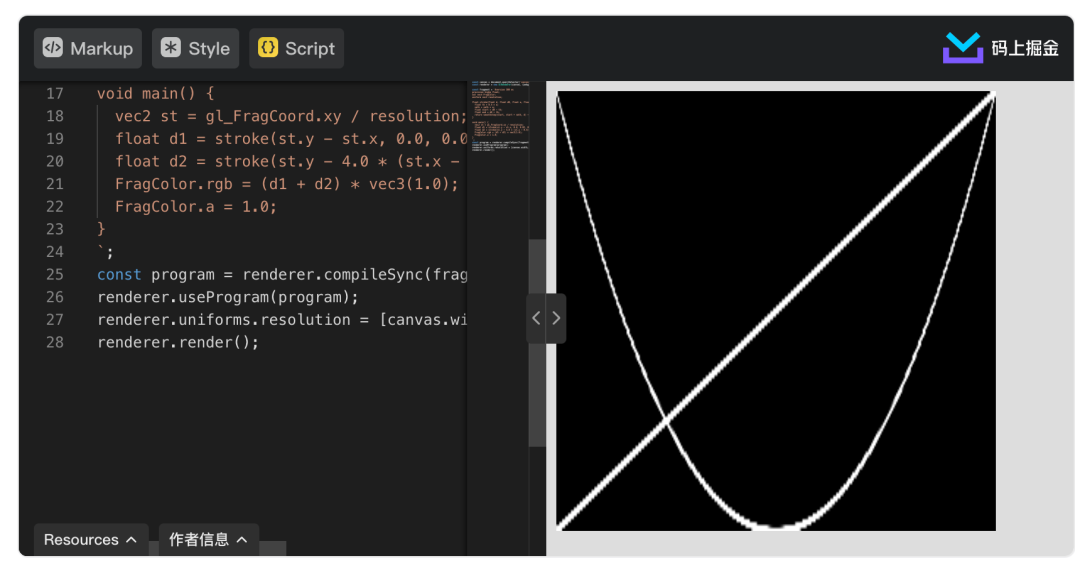
y=x的直线和y=4*(x-0.5)**2的抛物线:
https://code.juejin.cn/pen/7100862005245902884
参考资料
[1]简单多边形: https://www.baike.com/wiki/%E7%AE%80%E5%8D%95%E5%A4%9A%E8%BE%B9%E5%BD%A2/19923903?view_id=mywnwdgq41c00