463次阅读 | 发布于2年以前

本次分享大概分为下面几个方面

背景
贝塞尔曲线讲解
实现和探索过程

背景

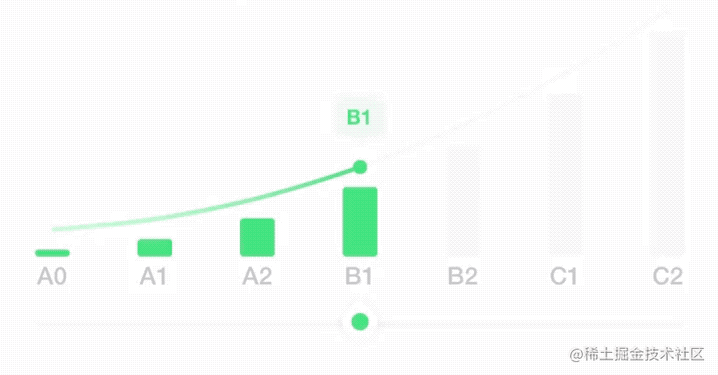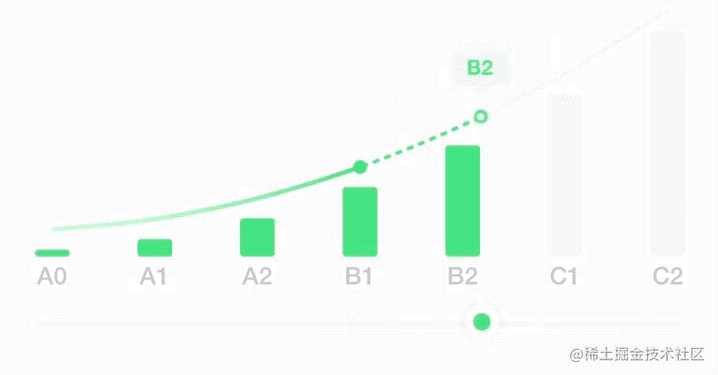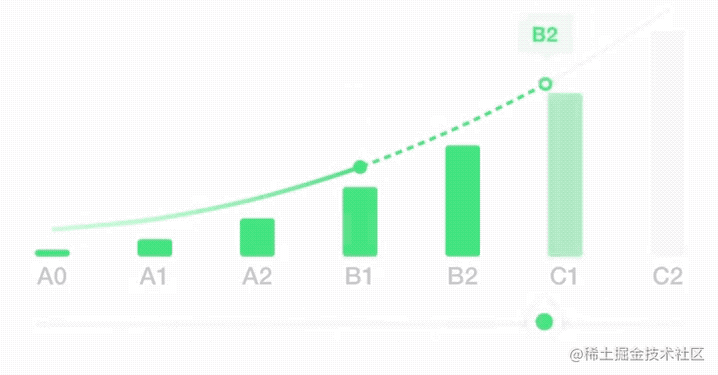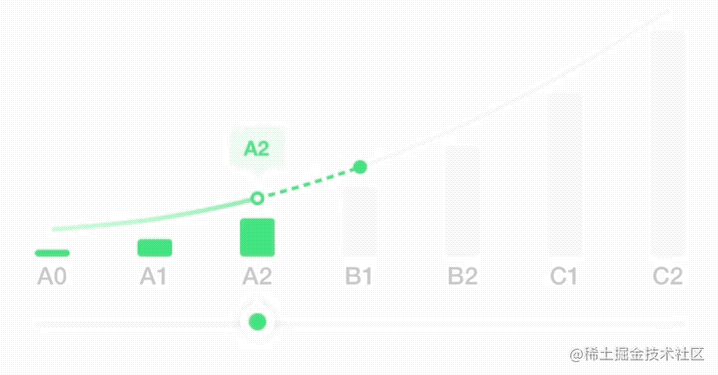
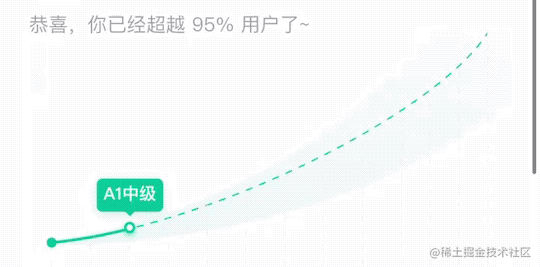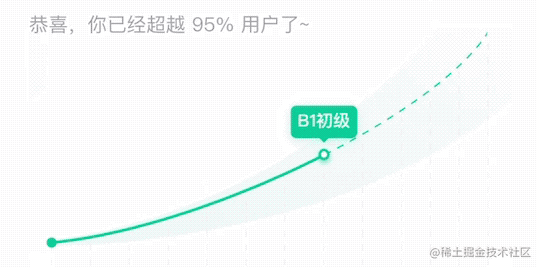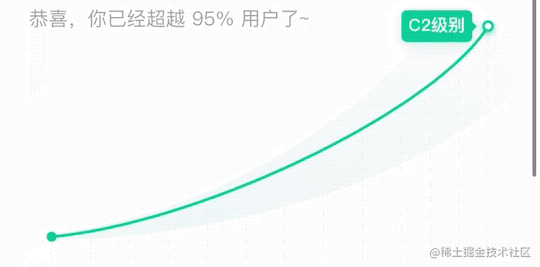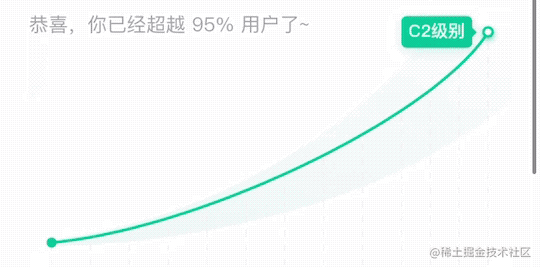
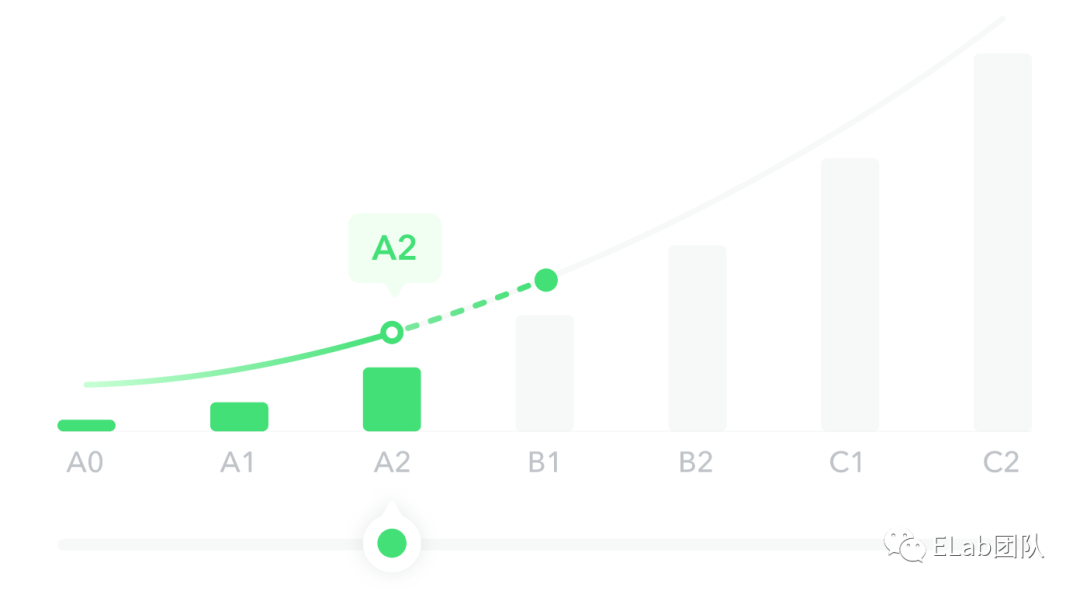
近期在 X 业务测评报告页有一个需求，用户可以左右拖动滑块来查看各个等级的信息。

在之前的野种中是通过切换图片的方式，会有卡顿的现象。由于 X 业务中等级区分比较少，等级间距更大，所以卡顿感会更大。

所以为了能够体现更丝滑的效果，使用svg画出贝塞尔曲线，动态控制实线和虚线的切换以及空心小球的位置。

svg中的path标签

<svg>
  <path 
      stroke="red" 
      fill="none"  
      d="M 4,130 C 12.85,129.1 45.3,126.7 63,124 C 80.7,121.3 104.3,116.5 122,1                        12 C 139.7,107.5 163.3,100.3 181,94 C 198.7,87.7 222.3,78.10000000000001 240,70 C 257.7,61.9 281.3,49.900000000000006 299,40 C 316.7,30.1 349.15,9.400000000000004 358,4"></path>
</svg>

M- moveto - 从一点移到另一点.（作为起点）

L- lineto -创建一条线.

H- horizontal lineto - 创建一条水平线.

V- vertical lineto - 创建一条竖线.

C- curveto - 创建(三阶)贝塞尔曲线到.

S- smooth curveto - 创建一条平滑曲线

Q- quadratic Bezier curve - 创建一个二次贝塞尔曲线

T- smooth quadratic Bezier curveto - 创建一个平滑二次贝塞尔曲线.

A- elliptical Arc - 创建一个椭圆弧.

Z- closepath - 关闭路径

上述命令使用大写字母，代表绝对路径，如果使用小写字母，则使用相对路径。

d="M 4,130 C 12.85,129.1 45.3,126.7 63,124".

贝塞尔曲线

贝塞尔曲线，由“线段”和节点组成，节点是可拖动的支点，表示曲线的趋向，“线段”像可伸缩的橡皮筋。它抽象了线段和曲线，通过控制路径上的四个点（起始点、终止点、两个中间点）来编辑图形；其中中间点和端点的连线称为控制线，这是一条虚拟的线段；两端的端点用来改变曲线的曲率；移动中间点来改变曲线运动轨迹。

一阶贝塞尔曲线

公式：B(t) = P1 + (P2 − P1)t = P1(1−t)+ P2t, t∈[0,1]

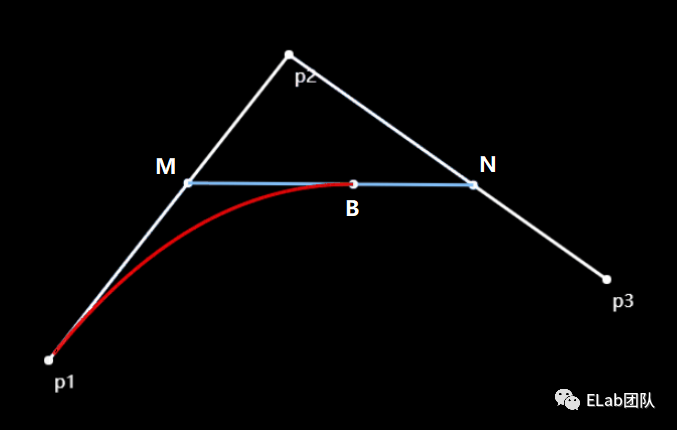
二阶贝塞尔曲线

在平面内选3个不同线的点P1、P2、P3并且依次用线段连接，P1，P3为固定点，P2为支点（控制点）

公式：

M = P1(1-t)+P2t

N = P2(1-t)+P3t

B(t) = M(1-t)+Nt

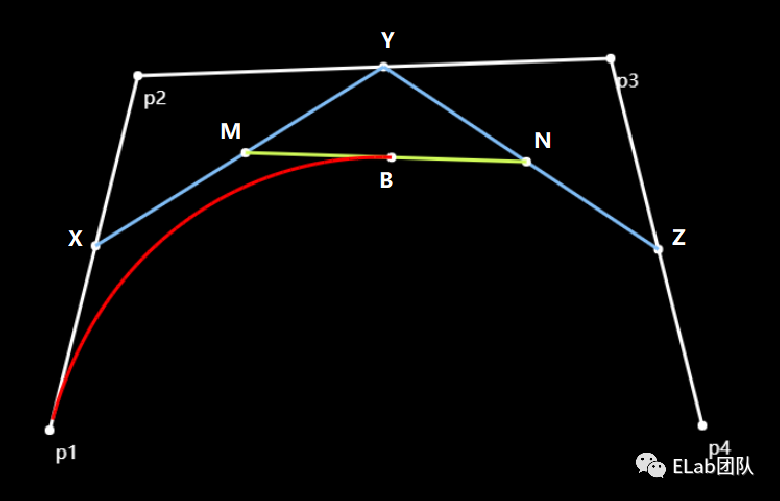
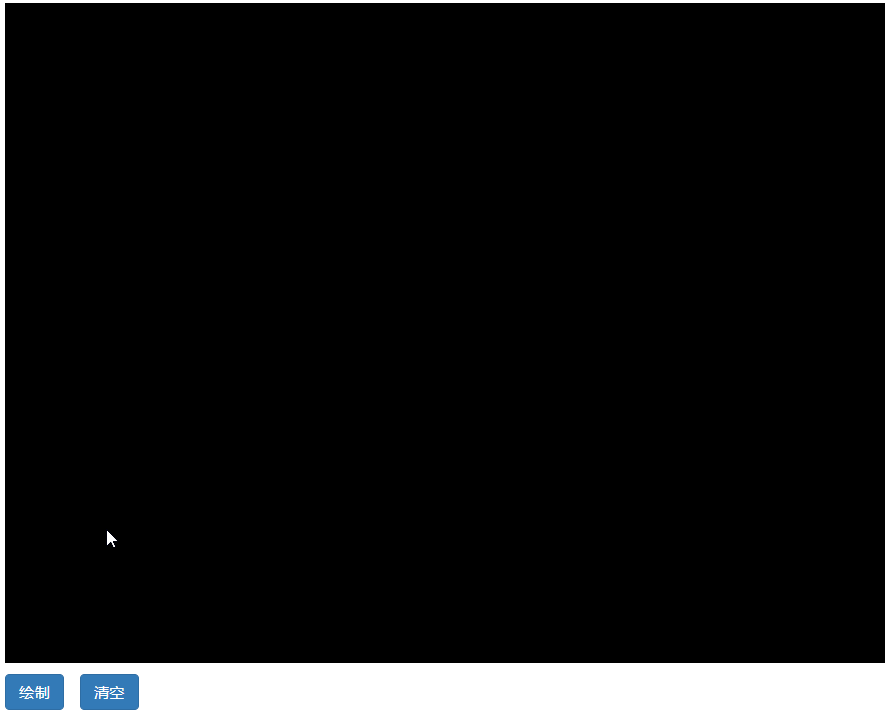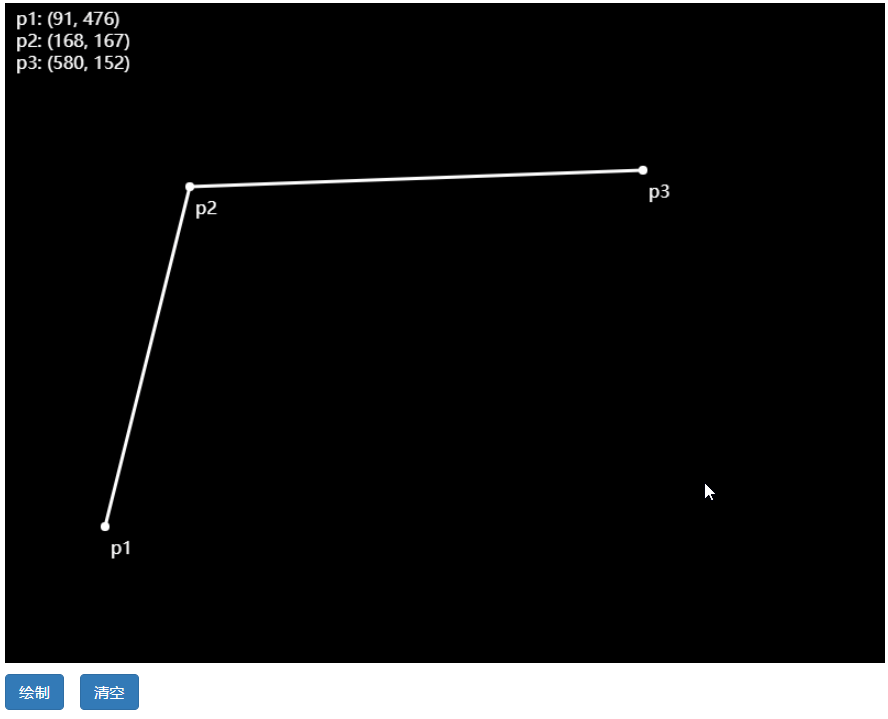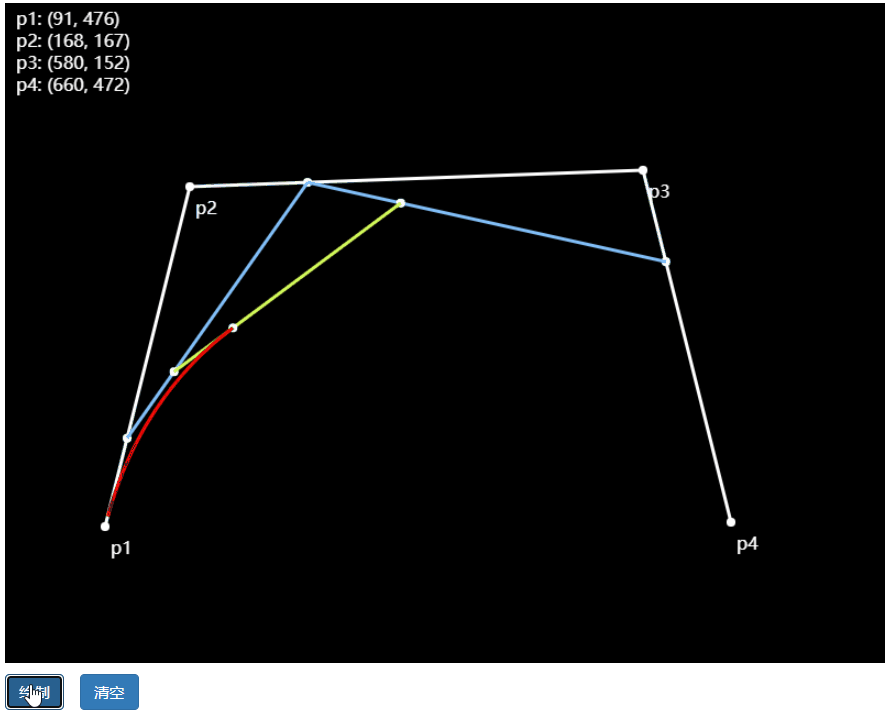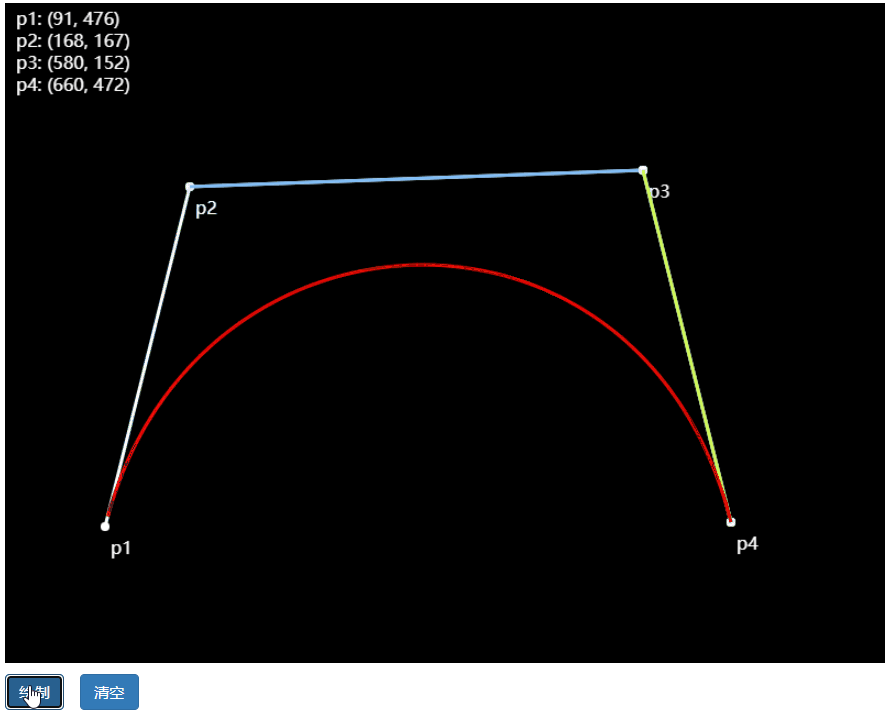
三阶贝塞尔曲线

公式：

X(t) = P(1)(1 - t) + P(2)t

Y(t) = P(2)(1 - t) + P(3)t

Z(t) = P(3)(1 - t) + P(4)t

M(t) = X(1 - t) + Yt

N(t) = Y(1 - t) + Zt

B(t) = M(1 - t) + Nt

N阶贝塞尔曲线

在三阶贝塞尔曲线中，如何确定控制点

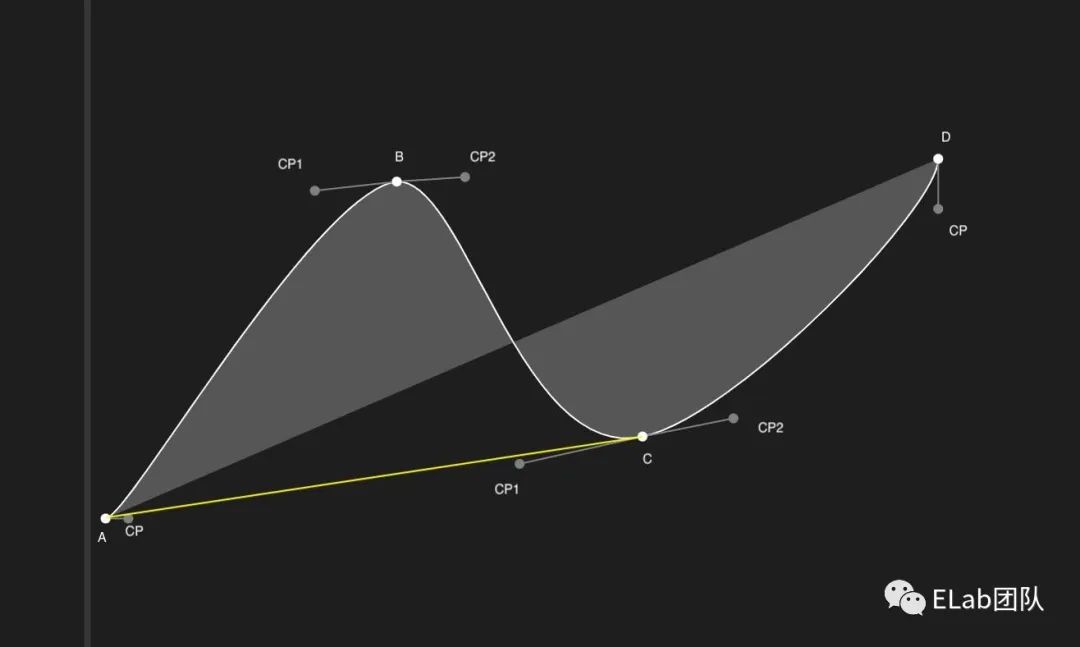
方向：越是高阶可导函数曲线越是光滑,在只要保证曲线函数试一阶导数连续，换句话说只要保证曲线的切线斜率连续，那么我们很容易确定CP（control point）点的所在直线的斜率。

长度: 长度决定了曲线弧度的大小（宽窄），有一种计算方式可以使曲线弧度很自然。

AC的长度 * smoothing, smoothing = 0.15比较光滑

对于第一个点A,和最后一个点D的控制点，可以简单把AB的方向看作是A点的切线方向，长度为AB*smoothing。同理可知道点D附近的控制点

实现动效的难点

跟手变化的时候，实线和虚线的切换
空心小球在曲线上跟手移动
松手后，小球和曲线的动画

SVG基础

stroke-dasharray 和 stroke-dashoffset

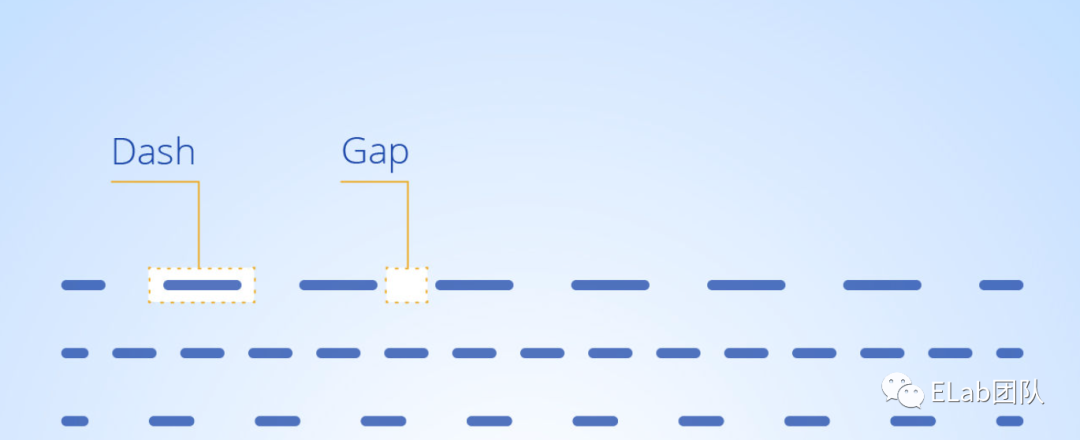
stroke-dasharray:用于创建虚线

a . 如：stroke-dasharray = '10, 5' 表示：虚线(Dash)长10，间距(Gap)5，然后重复虚线长10，间距5

b . 如：stroke-dasharray = '20, 10, 5' 表示：虚线长20，间距10，虚线长5，接着是间距20，虚线10，间距5，之后开始如此循环

2 . stroke-dashoffset：offset：偏移的意思

a . 这个属性是相对于起始点的偏移，正数偏移x值的时候，相当于往左移动了x个长度单位，负数偏移x的时候，相当于往右移动了x个长度单位。需要注意的是，不管偏移的方向是哪边，要记得dasharray 是循环的，也就是虚线-间隔-虚线-间隔。这个属性要搭配stroke-dasharray才能看得出来效果，非虚线的话，是无法看出偏移的。

如：https://codepen.io/Josh_byte/pen/MWQVWKK[1]

Offset-path和offset-distance css属性

通过css属性offset-path可以指定元素不规则的动画路径
offset-distance，是运动的距离，可以是数值或者百分比单位，如果是100%则表示正好把所有的路都跑完了。

如：https://codepen.io/Josh_byte/pen/PoQzjON[2]

参考：https://zhuanlan.zhihu.com/p/31242043[3]

兼容性

实现过程

step1 画贝塞尔曲线图

image.png BC直线的斜率与x1x2直线的斜率一致

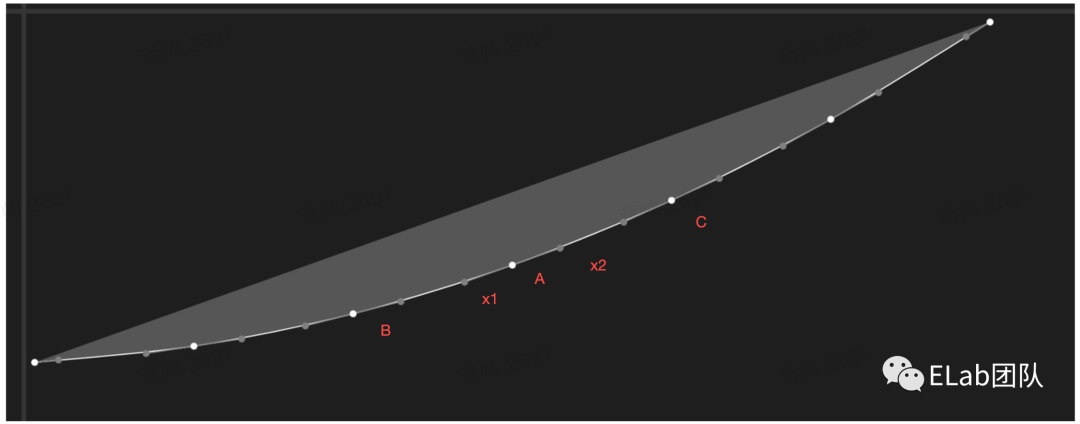
算圆心点坐标&把手坐标

//动态计算出的圆心坐标
const PointArray = [
[4, 130],
[63, 124],
[122, 112],
[181, 94],
[240, 70],
[299, 40],
[358, 4]
]


//算出当前点前一个点和后一个点的角度
const line = (pointA: number[], pointB: number[]) => {
    const lengthX = pointB[0] - pointA[0];
    const lengthY = pointB[1] - pointA[1];
    return {
      length: Math.sqrt(Math.pow(lengthX, 2) + Math.pow(lengthY, 2)),
      angle: Math.atan2(lengthY, lengthX),
    };
  };

//求每两个圆心坐标之间的两个把手
const controlPoint = (current: number[], previous: number[], next: number[], reverse: boolean) => {
    const p = previous || current;
    const n = next || current;
    const l = this.line(p, n);

    const angle = l.angle + (reverse ? Math.PI : 0);
    const length = l.length * BezierCurveAndCirclePoint.smoothing;
    const x = current[0] + Math.cos(angle) * length;
    const y = current[1] + Math.sin(angle) * length;
    return [x, y];
  };

const getBezierCurvePointArray = () => {
    const array: Point[][] = [];
    pointArray.forEach((item, i) => {
      if (i === 0) {
        return;
      }
      const cps = this.controlPoint(this.pointArray[i - 1], this.pointArray[i - 2], item, false);
      const cpe = this.controlPoint(item, this.pointArray[i - 1], this.pointArray[i + 1], true);
      array.push([
        {
          x: pointArray[i - 1][0],
          y: pointArray[i - 1][1],
        },
        {
          x: cps[0],
          y: cps[1],
        },
        {
          x: cpe[0],
          y: cpe[1],
        },
        {
          x: item[0],
          y: item[1],
        },
      ]);
    });
    return array;
};

绘制三条三阶贝塞尔曲线

观察发现

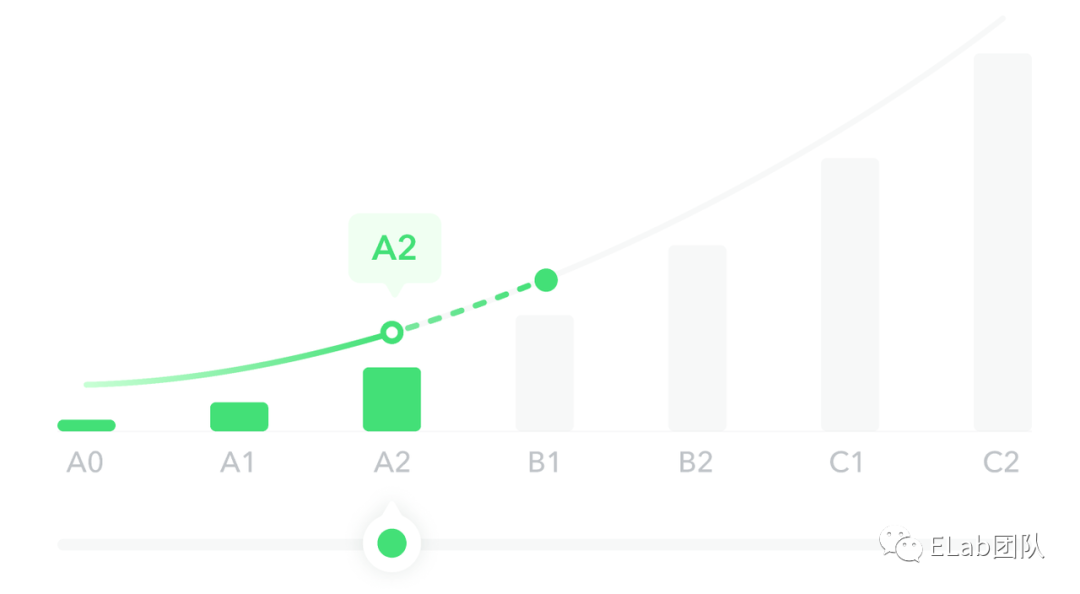
绿色实线变绿色虚线的过程可以看成，绿色实线往左偏移的过程（stroke-dashoffset)

灰色实线变绿色虚线的过程，可以看成，灰色实线往右偏移的过程。

绿色虚线，在最底层，没有变化。变化的是绿色和灰色实线

案例 https://codepen.io/Josh_byte/pen/bGLvKYM[4]

step2 求曲线弧长

如何判断stroke-dashoffset的距离？跟手移动2px，绿色实线或灰色实线移动多少？

stroke-dasharray的初始值设置为多少？

如何求三阶贝塞尔曲线函数的坐标

P0 是起始点坐标

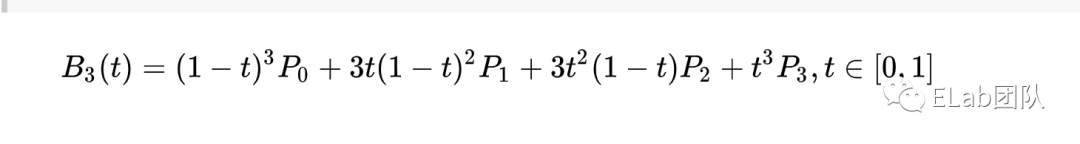
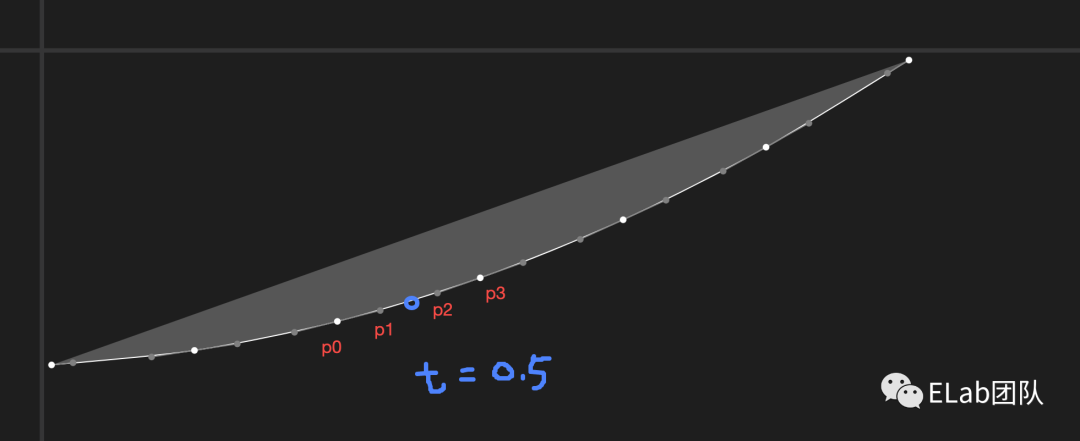
P1,P2是控制点

P3是终点坐标

t是百分比（在曲线位置的百分比）

const calculateCirclePoint = (t: number, PointArray: Point[]) => {
    const p0 = PointArray[0];
    const p1 = PointArray[1];
    const p2 = PointArray[2];
    const p3 = PointArray[3];
    const temp = 1 - t;
    const x =
      p0.x * temp * temp * temp +
      3 * p1.x * t * temp * temp +
      3 * p2.x * t * t * temp +
      p3.x * t * t * t;
    const y =
      p0.y * temp * temp * temp +
      3 * p1.y * t * temp * temp +
      3 * p2.y * t * t * temp +
      p3.y * t * t * t;
    return {
      x,
      y,
    };
  };
//举个例子，第一段曲线
const curvePoint = 
[{x: 122, y: 112}, //起始点
{x: 139.7, y: 107.5}, //把手一
{x: 163.3, y: 100.3}, //把手二
{x: 181, y: 94}]。//终点
calculateCirclePoint(0.5,curvePoint)

如何求弧长

采样大概估算弧长，一段曲线中等间距采点60个，每两个点计算的间距求和

const cubicBezierLength = (PointArray: Point[], sampleCount?: number) => {
    const ptCount = sampleCount || 40;
    let totDist = 0;
    let lastX = PointArray[0].x;
    let lastY = PointArray[0].y;
    let dx;
    let dy;
    for (let i = 1; i < ptCount; i++) {
      const pt = this.calculateCirclePoint(i / ptCount, PointArray);
      dx = pt.x - lastX;
      dy = pt.y - lastY;
      totDist += Math.sqrt(dx * dx + dy * dy);
      lastX = pt.x;
      lastY = pt.y;
    }
    dx = PointArray[3].x - lastX;
    dy = PointArray[3].y - lastY;
    totDist += Math.sqrt(dx * dx + dy * dy);
    return Math.floor(totDist);
  };

完成以上两步，就可以实现曲线跟手移动的变化还有松手时候的动效了。

step3 实现空心小球跟手移动

由于offset-path属性在ios上不支持，只能实时求空心小球的实时坐标

step4 实现空心小球松手后的吸附动效

SVG SMIL animation

1 . animateMotion/

 <circle
    opacity={circleAnimationPointOpacity ? '1' : '0'}
    r="3"
    fill="#ffffff"
    strokeWidth="2"
    stroke="#43E077"
    >
            <animateMotion
              ref={circleAnimationRef}
              path={cirlceAnimationPath} //运动路径 
              dur="200ms"   //持续时间
              keySplines="0.25 0.1 0.25 1" //动画时间曲线
              fill="freeze".    //结束后在原位置
              begin="indefinit".   //无限等待 开始用circleAnimationRef.current.beginElement()
              repeatCount="1".  //执行一次
            />
 </circle>

案列 https://codepen.io/Josh_byte/pen/oNEYpjO[5]

2 . 有两个空心绿色小球，一个小球是跟手移动的空心小球，还有一个是实现松手后动画的空心小球。

参考资料

[1]https://codepen.io/Josh_byte/pen/MWQVWKK: https://codepen.io/Josh_byte/pen/MWQVWKK

[2]https://codepen.io/Josh_byte/pen/PoQzjON: https://codepen.io/Josh_byte/pen/PoQzjON

[3]https://zhuanlan.zhihu.com/p/31242043: https://zhuanlan.zhihu.com/p/31242043

[4]https://codepen.io/Josh_byte/pen/bGLvKYM: https://codepen.io/Josh_byte/pen/bGLvKYM

[5]https://codepen.io/Josh_byte/pen/oNEYpjO: https://codepen.io/Josh_byte/pen/oNEYpjO

贝塞尔曲线轨迹运动原理与实战

背景