浅析神经网络 Neural Networks
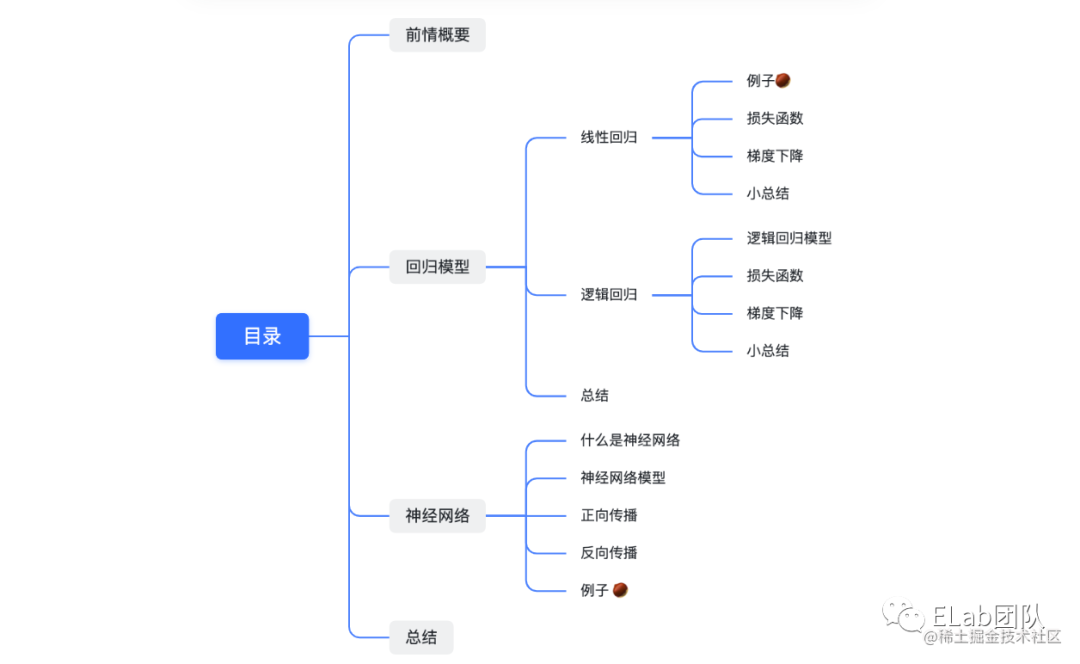
目录
前情概要
- 该主题分享的目的是:
- 不局限于前端,拓展知识学习领域,不设边界。
- 以下仅代表我个人学习总结,如有问题,虚心请教,并及时修正。
另外本次分享不会有大段大段代码,主要是理解为什么这么做。
在开始分享主题之前,我们可以先思考下,不管你用什么语言 (解释类型语言 或 编译类型语言),你写一堆的字符串,一顿解析编译后,从汇编语言再到最后的机器语言 0 / 1,即是CPU"认识"的。CPU用来计算和控制计算机系统的一套指令的集合。电路实现这种运算。运算又是规则。以上,每一个步骤的描述都是为了应对日益复杂的问题,不断抽象的过程。
不管我们怎么抽象,都离不开计算,计算又离不开数学(利用抽象和逻辑能力) 。我们今天主题跟抽象、计算、数学这几个词,是很有关系的。
回到本次分享的主题,人工智能又是什么?简单的说是有海量数据 -> 归纳出规则 -> 解决问题。
Artificial intelligence is intelligence demonstrated by machines.
你会想这跟智能没啥关系啊 ~ 我个人理解智能是玄学,那人工智能是什么?
统计学: 是应用数学的一个分支,主要通过利用概率论建立数学模型,收集所观察系统的数据,进行量化的分析、总结,并进而进行推断和预测,为相关决策提供依据和参考。
Statistics is the study and manipulation of data, including ways to gather, review, analyze, and draw conclusions from data.
人工智能包括机器学习,例如线性回归、逻辑回归、贝叶斯模型、NN等。通过某个模型结构,基于训练数据,得出相应关系的概率。深度学习又是机器学习的一个分支,是基于NN神经网络为基本架构的拓展,常见的CNN(图像处理)、RNN(语音识别)等。
概念上就不做过多解释了,我直接上参考的结论吧。
参考:
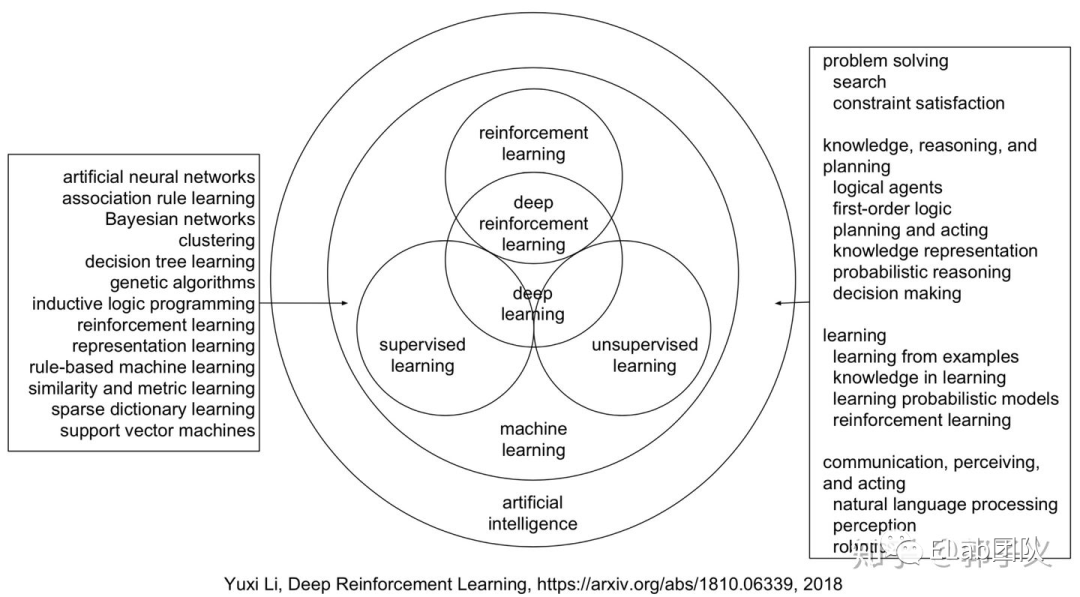
- 机器学习、深度学习和强化学习的关系和区别是什么? - 知乎[1]
- DEEP REINFORCEMENT LEARNING.pdf[2]
- 机器学习:一切通过优化方法挖掘数据中规律的学科。
- 深度学习:一切运用了神经网络作为参数结构进行优化的机器学习算法。
- 强化学习:不仅能利用现有数据,还可以通过对环境的探索获得新数据,并利用新数据循环往复地更新迭代现有模型的机器学习算法。
- 深度强化学习:一切运用了神经网络作为参数结构进行优化的强化学习算法。
前情概要的小总结: 应对海量数据,我们需要通过一些方法 (工具? 抽象能力?计算?算法、数学?...),俗称AI,来帮助我们解决问题。
回归模型
线性回归
例子
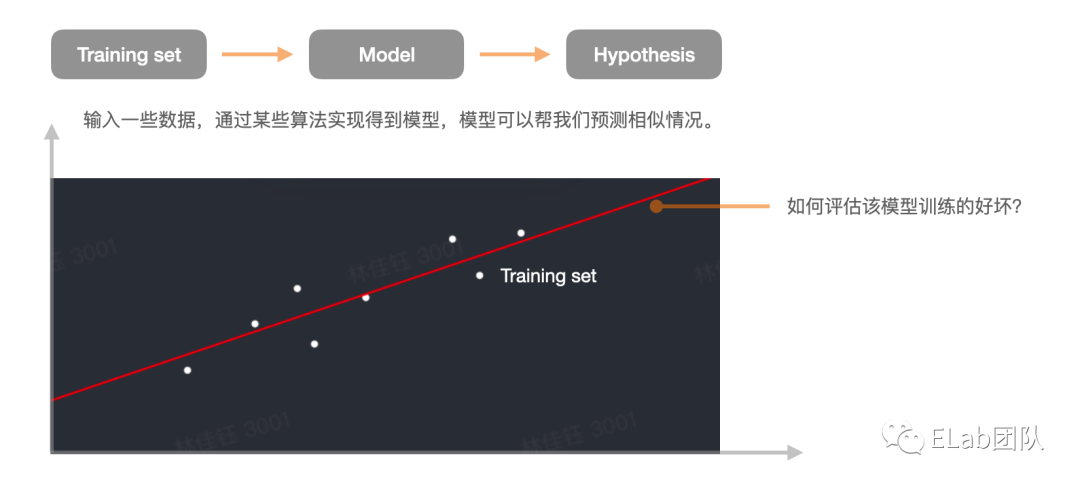
我们先通过一个简单的例子,来看基于tensorflow.js实现的线性模型。
https://linjiayu6.github.io/Tensorflow.js-LinearRegression/
首先,在屏幕上点几个离散点。

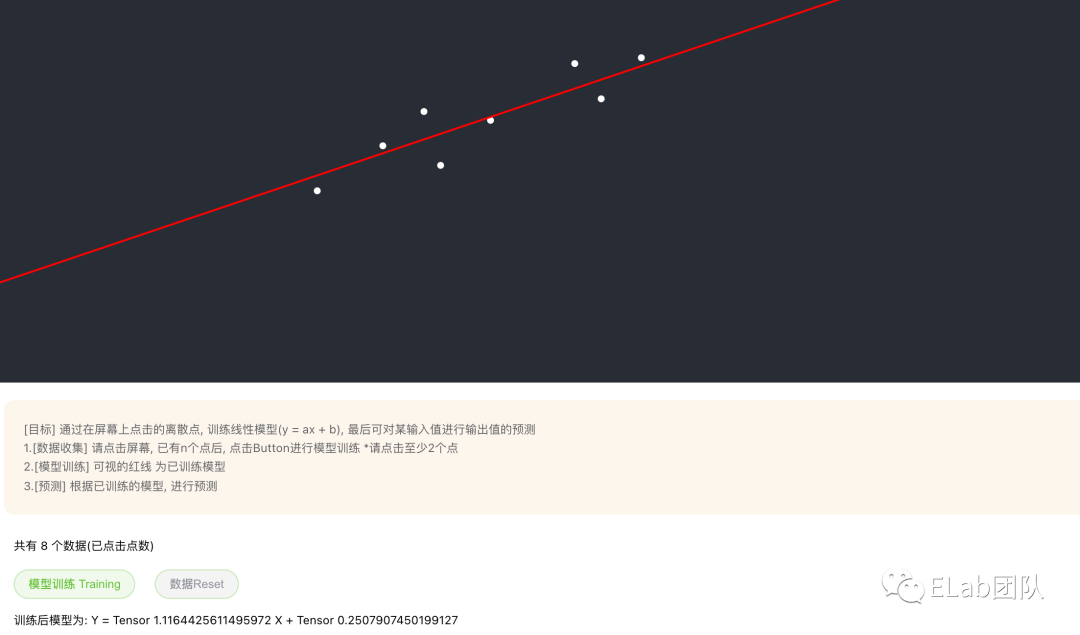
- 看到这里你会问,这怎么实现?我们来看看 代码[3]。
- 确认模型 y = ax + b
- x, y 数据需要处理成矩阵,叫做x特征值,y是实际结果值。
- a,b 是需要我们通过某种方法预测出来的值。
- 训练模型 涉及 损失函数、梯度下降等。
- 得到训练好的模型。
import * as tf from '@tensorflow/tfjs'
window.a = tf.variable(tf.scalar(Math.random()))
window.b = tf.variable(tf.scalar(Math.random()))
// 建立模型 y = ax + b
const model = (xs, a, b) => xs.mul(a).add(b)
// 1. training, y值
const training = ({ points, trainTimes }) => {
for (var i = 0; i < trainTimes; i++) {
const learningRate = 0.1 // 学习率
const optimizer = tf.train.sgd(learningRate); // 随机梯度下降
const ys = tf.tensor1d(points.map(points => points.y)) // 样本y值
// loss(训练好的模型y'值 - 样本y值)的损失到最小。
optimizer.minimize(() => loss(predict(points.map((points) => points.x)), ys));
}
}
// 2. predict, x值输入, 线性方程 y = ax + b
const predict = x => {
return tf.tidy(() => {
const xs = tf.tensor1d(x)
const predictYs = model(xs, window.a, window.b)
return predictYs
})
}
// 3. 评价过程, 也是损失函数: 均方差 求出最小的
const loss = (predictYs, ys) => predictYs.sub(ys).square().mean()
export default {
training, predict
}
损失函数
损失函数是用来评估模型的好坏,即模型预测值和真实值的误差, 损失越小, 模型越好。We measure the "accuracy" of our hypothesis function by using a cost function
平方误差函数 广泛应用在 回归的问题 square error function is commonly used for "regression" problems

损失函数: 用于度量建模误差的,为了得到误差的最小值。统计学中通常使用平方误差方法。
统计学中的平方误差(损失)函数
- θθθ
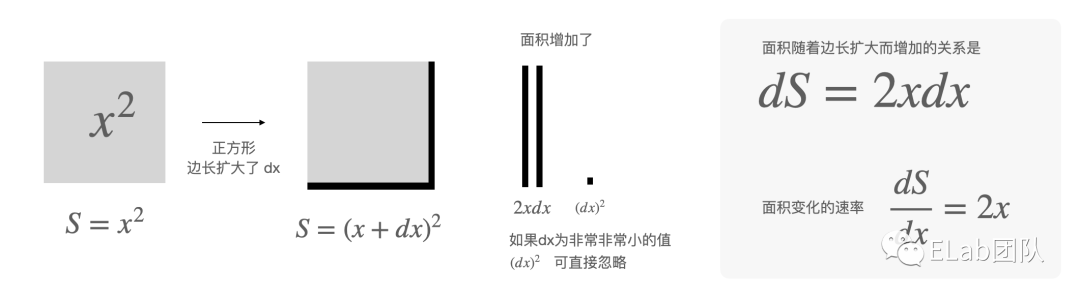
- 系数是为了后续在梯度下降中便于求解使用的。导数会抵消掉
梯度下降
梯度下降还会涉及到 特征值缩放、均值归一化处理等。这里也不做过多扩展。
- 好处是: 每个特性向量值均缩放到一个区间内,梯度下降速度会更快。
想象你在山顶上了,需要下山,有很多条道儿可以走。
- 如果你步伐迈的太大,意味着你可能会很快下山,但也有可能走太多的弯路,花费更多时间。
- 如果你步伐迈的太小,意味着你可能不能很快下山,但也可能会在过程中找到最佳下山路径,用了最少时间。

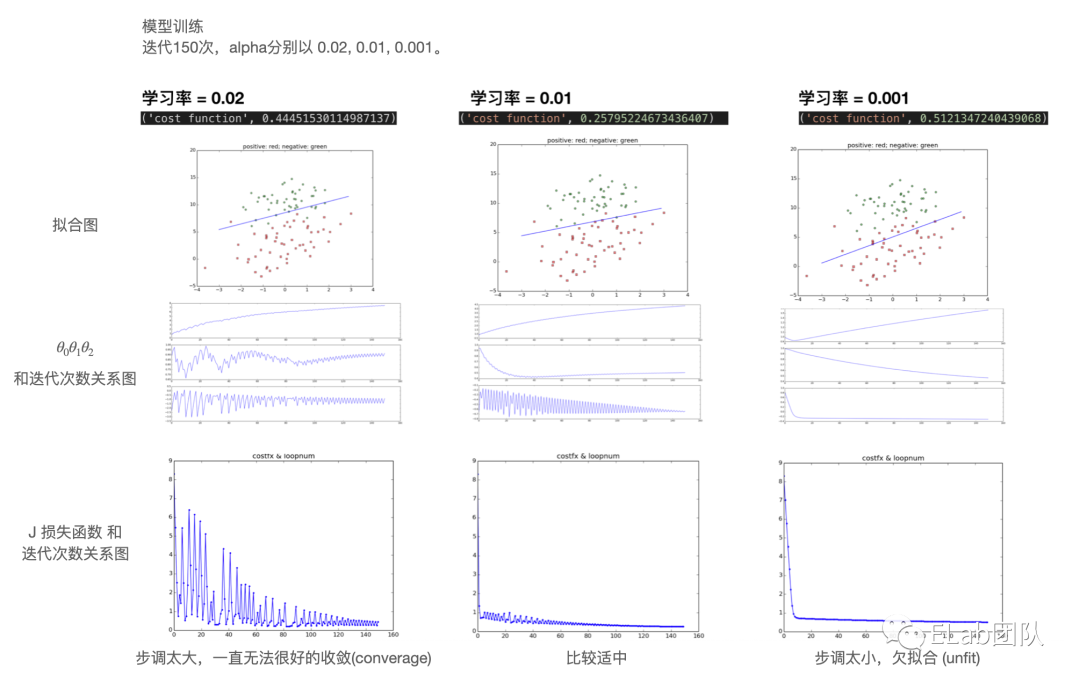
该例子通过图像直观说明学习率(步伐多大)对模型的影响 (eg: 收敛、欠拟合)。
梯度下降目的: 用来求解损失函数的最小值的方法。得到局部最优解的方法。

| 类比 | ||
|---|---|---|
| 线性回归模型 | θθθ | |
| 目标是 | 下山 | θθ |
| 损失函数表示 | 下山如何费力最小 | |
| 梯度下降(Repeat) | 具体细节:α 步子迈多大 θθθ 每次朝着哪个方向走经过不停的调整步伐和下山的方向,最后成功下山,并以最小费力方式。 | θθαθθθ Repeat until converage 以上结论,计算推导过程。高数知识只要知道复合函数求导就ok了。 |
小总结
我们再来回顾下刚才的代码例子。
1 . 确认目标: 你此刻站在山顶⛰,规划下山路径(θθθ),想要下山(θθ)
2 . 在你没有开始行动前,就已经得到了下山最不费力的方法(损失函数))
3 . 当你走每一步,会调整下山步伐α 和方向 θθθ 的规划
a . (梯度下降 θθαθθθ)
4 . 不停的重复第三步,最后成功下山。
是不是看到这里,发现模型的训练,也没有那么难啦。
逻辑回归
在线性回归模型中,我们了解到了模型、损失函数、梯度下降的含义。
逻辑回归对我们理解NN 神经网络有很大的帮助。
逻辑回归的现实意义是分类问题。eg: 预测用户是否喜欢该类视频?预测该用户是男还是女?
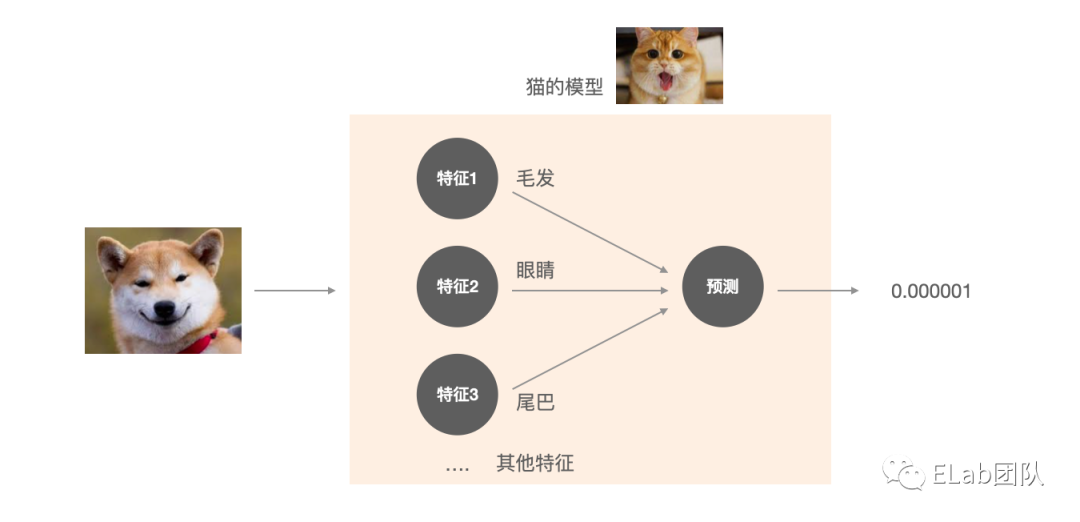
例如我们预测该图片是否是只猫:
- 模型: 我们有 n个猫的特征features (毛发、眼睛、鼻子.... ),通过这些特征来预测一个图片是否是猫。
- 预测的结果标识 / 逻辑回归: θ,有多大的概率。
- 从模型和预测的结果来看,已经不是线性模型可以覆盖到的情况了。下面介绍下逻辑回归的模型。
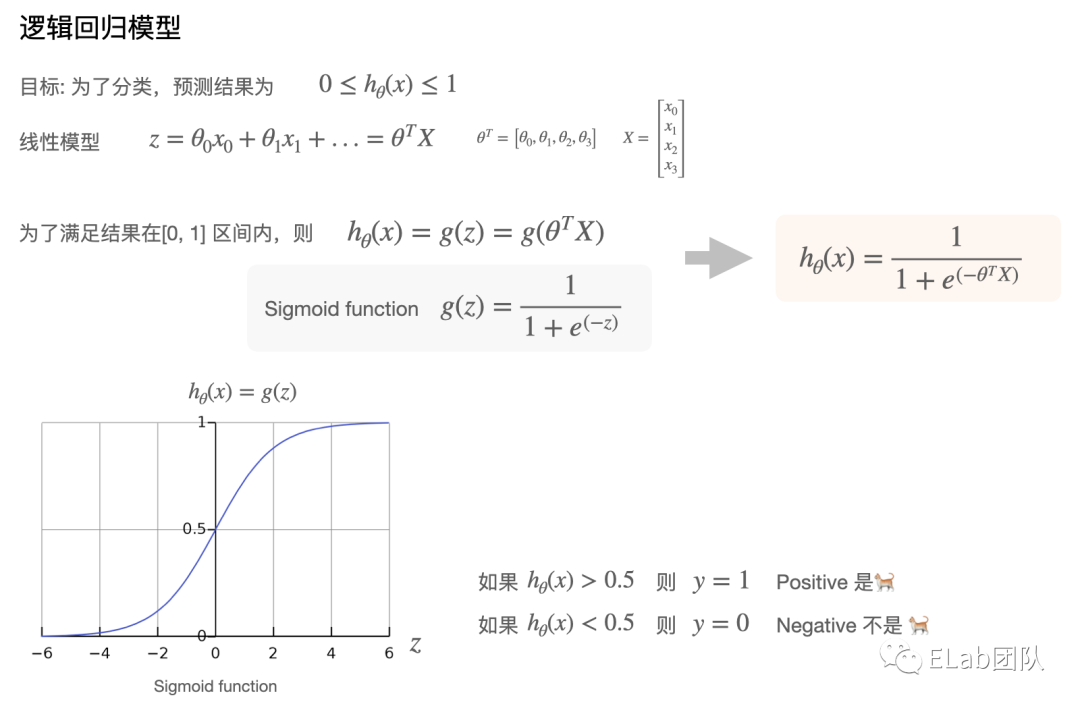
模型
如果要实现上述例子,就需要明白逻辑回归的模型。
除了sigmoid,还有一些其他方法例如 relu tanh,在NN中被使用。
损失函数
逻辑回归和线性回归的损失函数是不同的。线性回归损失函数(平方损失函数) 是在在满足高斯分布 / 正态分布[5]的条件下推导得到的,而逻辑回归假设样本满足伯努利分布[6]。故需要重新定义损失函数。
损失函数为: (是从 最大似然估计[7] 得来的)
简单解释下损失函数的含义:
- 对单一样本
- 预测结果只有 是和不是 两种情况,即 或 。
- 展开后为
| y | 损失函数 | 损失函数 和 之间关系 |
|---|---|---|
| 代入公式 => | 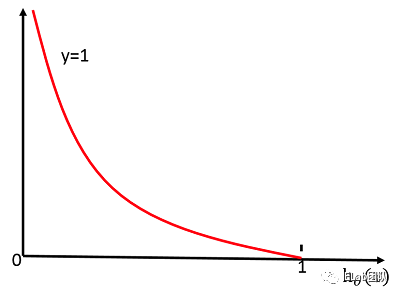 当预测值 ,误差为0。反之随着 变小误差变大。 当预测值 ,误差为0。反之随着 变小误差变大。 |
|
| 代入公式 => | 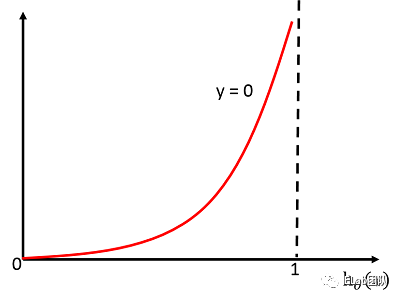 当预测值 ,误差为0。反之随着 变大误差变大。 当预测值 ,误差为0。反之随着 变大误差变大。 |
有了损失函数的定义后,和线性回归一样的道理,我们需要计算出 损失函数 最小的时候 值。
梯度下降

小总结
| 逻辑回归模型 | 1. θθθθ θθθθθθ 2. Sigmoid Function 3. θθ 值在[0, 1] |
|---|---|
| 目标是 | θθθθθθ |
| 损失函数 | |
| 梯度下降 | θ θ α θ θ θ Repeat until converage 以上结论,计算推导过程。高数知识只要知道复合函数求导就ok了。 |
总结
我们大致了解了线性和逻辑回归的模型,也理解了损失函数和梯度下降的意义。
但面对着日益复杂的情况,如此简单的模型是无法满足现实情况的。尤其当特征值很多的时候,即 对计算是非常大的负荷。例如我们对一张图片进行预测是否是车,如果该图片像素是100*100 *3, 即有3w个特征值,这显然对计算来说是很不合理的。
这也就是为什么,我们需要神经网络NN,以及CNN、RNN 等这些更复杂的模型。
神经网络
学习资料: 3blue1brown-深度学习(英文搬运)_哔哩哔哩_bilibili[9]
什么是神经网络
生物上的神经元,有输入和输出层,输入层接受其他神经元的信息,输出层以电脉冲的形式发给其他神经元。
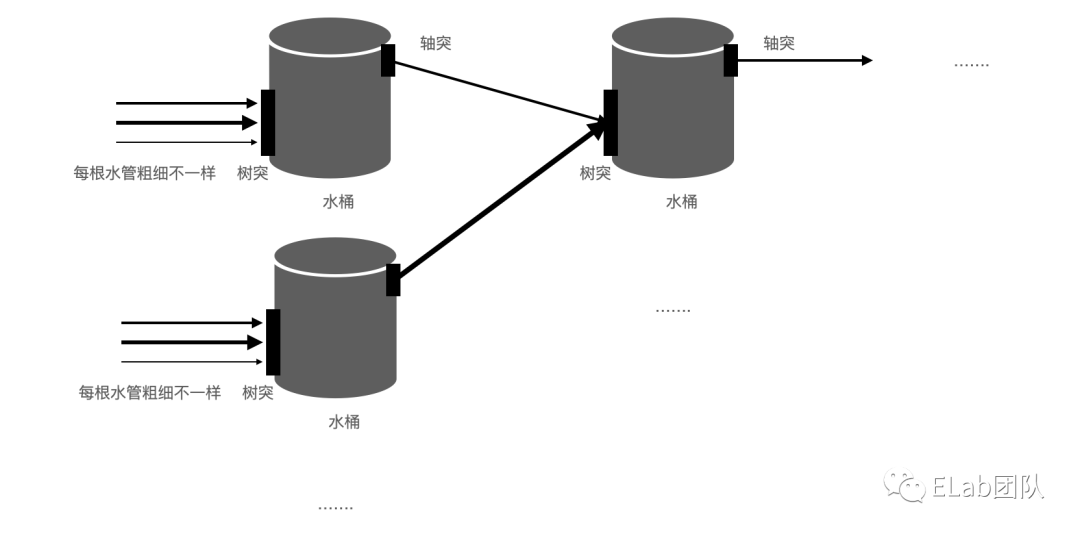
当大脑在思考的时候,一枚可爱的神经元在干什么? 每个树突收到其他神经元发出的刺激脉冲后,当这些刺激脉冲叠加后,达到一定的强度阈值,就会产生动作电位,并沿着轴突发送电信号。故以此来不停的传递。
该过程可类比于有很多条水管(树突),水管粗细不一,故输入的流速也不一样,开始放水(信号),当水桶里水足够多并达到阈值的时候 (激活),会从右侧轴突流出来。流出的水会再次流向下一个水桶。
Neural Networks: 算法来模拟人的大脑。本质还是构建模型,并通过数学运算得到预测结果。人认识某个动物是大熊猫是一样的,我们对熊猫的特征认知,例如大熊猫只有黑白色、只在四川、只吃竹子等等。故对NN模型的训练道理是一样的。
NN 神经网络是最基本的的算法模型,像深度学习的CNN 卷积神经网络对图像的处理;RNN 循环神经网络对语言模型的研究等等,各种复杂的模型,都是基于NN拓展的。
神经网络模型
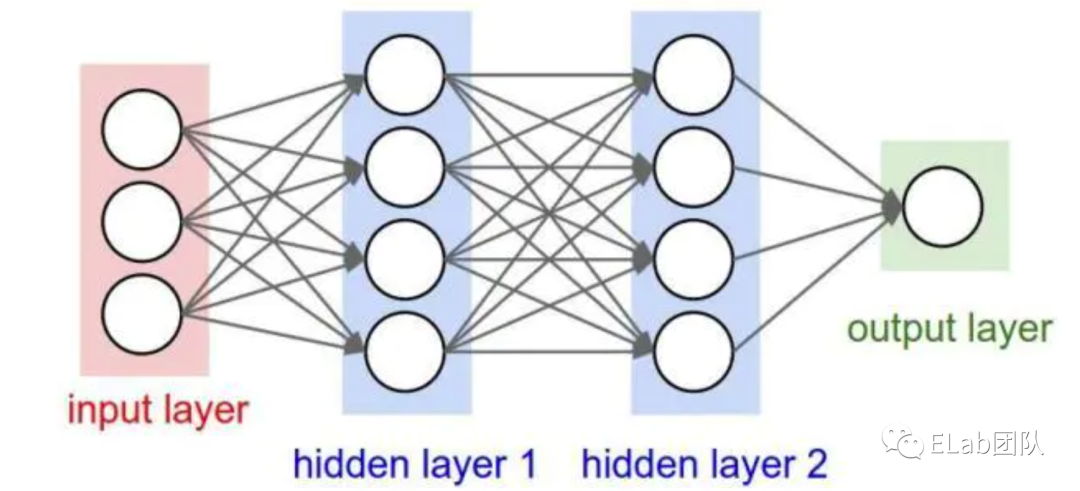
- 1个输入层: Input Layer。eg: 图上输入层有3个特征值。
- N隐藏层: Hidden Layers。eg: 图上有两个隐藏层。
- 1个输出层: Output Layer。eg: 对某个结果的预测。
每一层都有很多个神经元 Neuron。对于一个神经元的结构如下:
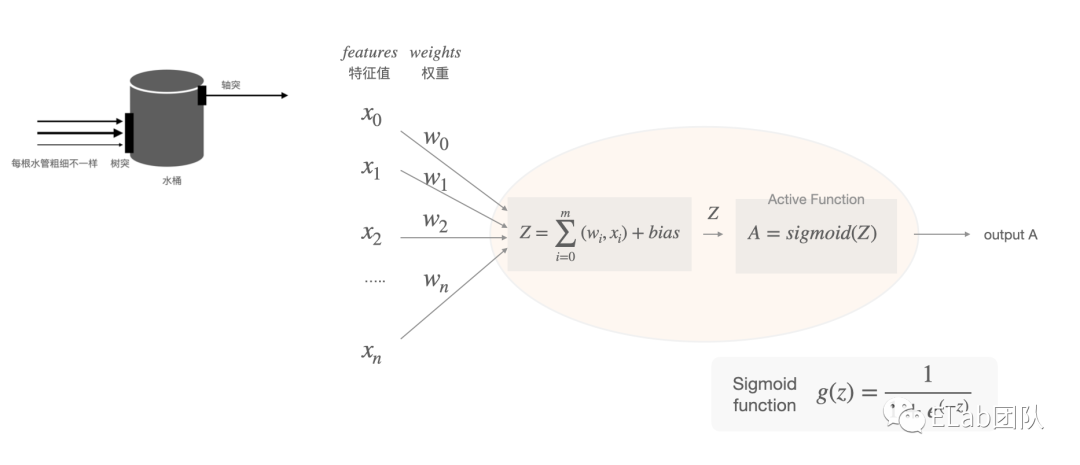
说明:
- 特征值 features:
- 权重值 weights: 每个神经元连接的线 (概念也可以理解为 )
- 偏移量 bias: 偏移量增加的意义[10]
- 激活函数 activation function 例如常见的sigmoid、tanh、Relu方法
一个神经元内部计算:
是不是也不难看懂,其实每一个小的神经元,类似一个逻辑回归。
通常对于激活函数 activation function,如图上使用 sigmoid的使用,会使用Relu。
正向传播
创建模型,定义每层的结构,并以此往后传递。
简单的理解是: 将多个逻辑回归模型组合在一起。

Eg: (只是个例子说明) 该模型是预测是猫还是狗,X 特征值代表 毛发、眼睛、鼻子、嘴巴,输出层会判断猫还是狗的概率更大些。
针对已经建立的模型,像逻辑回归一样,明确每一个神经元连接的信息。
例如 按照我们上面对一个神经元模型的创建,建立每个神经元的公式。
以下为了理解 激活函数 activation function用了 sigmoid function
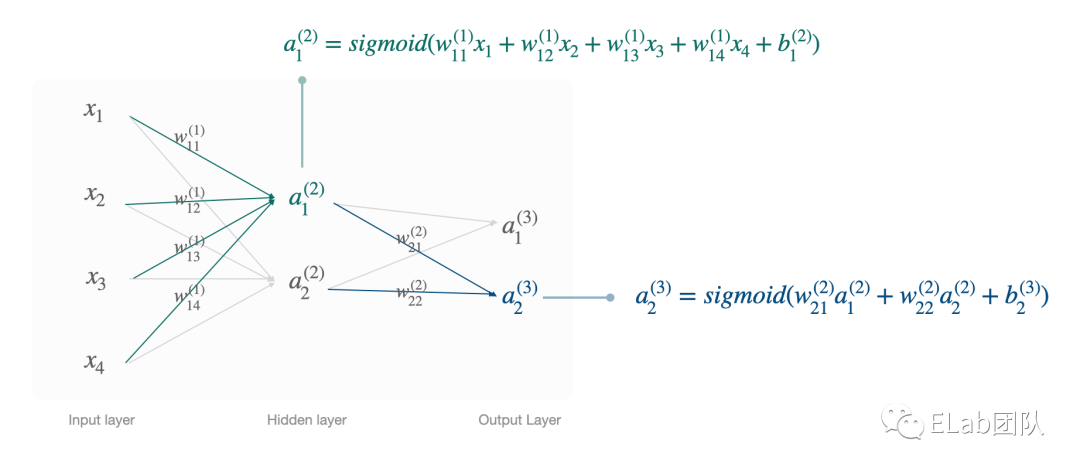

此时,我们的目标值是每一层的 W 和 b。
反向传播
按照我们回归模型的套路是,在已经创建好的模型基础上,评估损失函数。
其实理解了逻辑回归的损失函数,不难理解这个公式。
我们暂不去看正则化的处理 (正则化我的理解是: 向模型加入某些规则,加入先验,缩小解空间,减小求出错误解的可能性)。NN损失函数的定义非常的明确,是每个分类的损失函数加和。

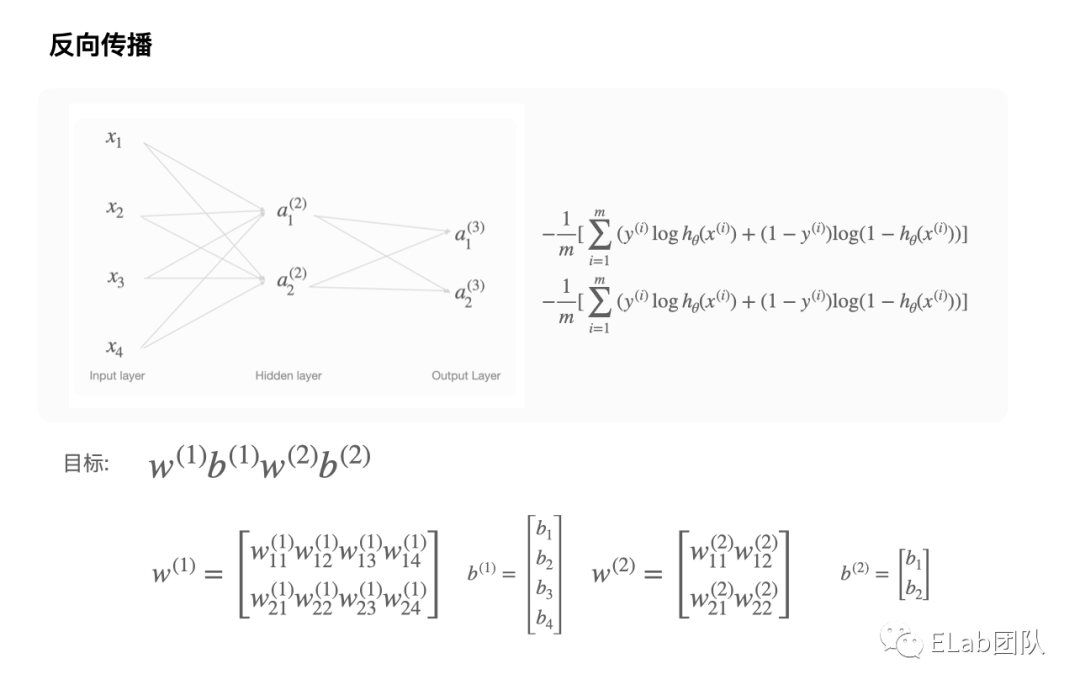

- α
- α
- α
- α
例子
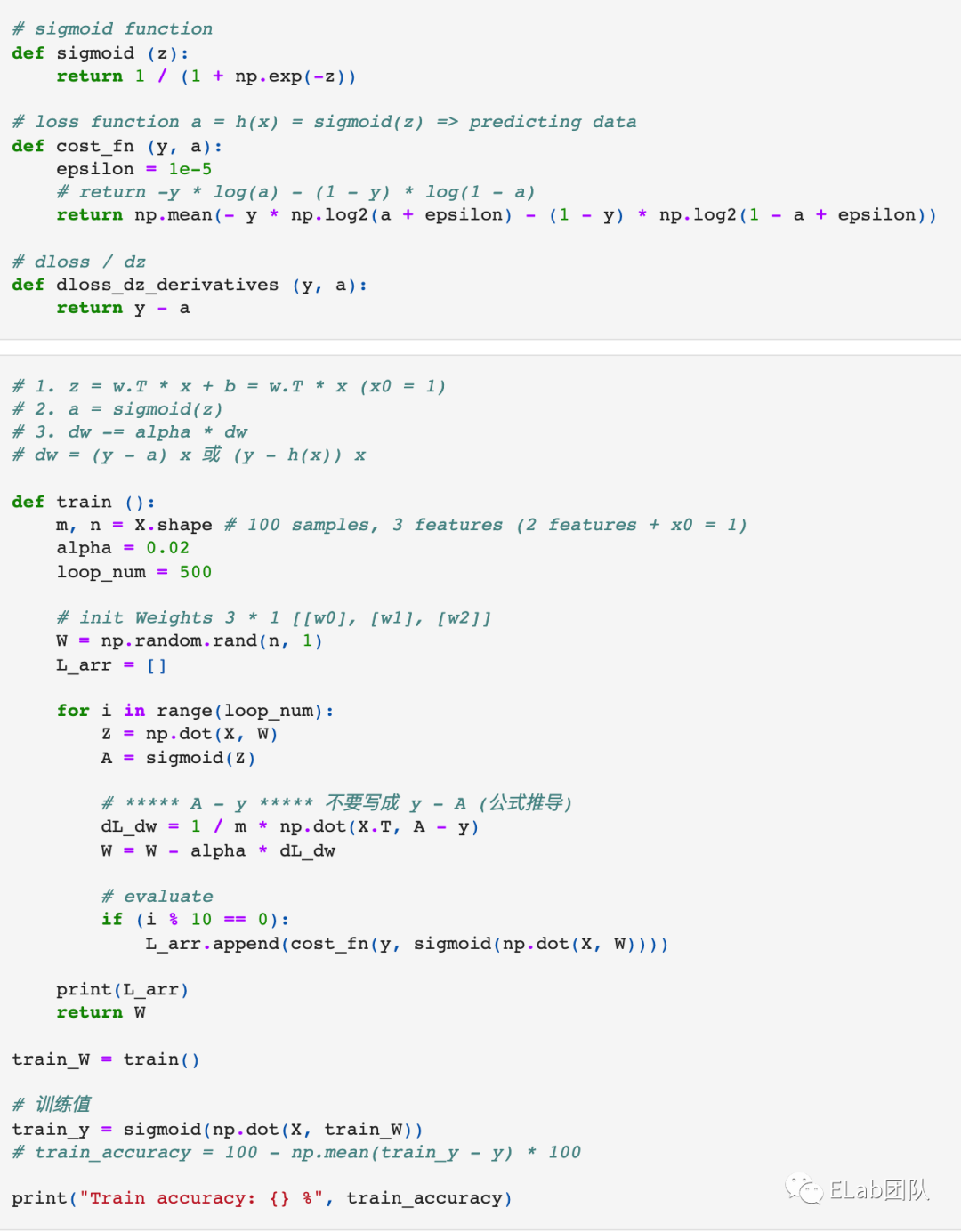
代码: 用NN识别一只[11],以下为代码片段。
- 加载数据、处理数据。省略代码说明。
- 建立模型,定义向前传播。
# Sigmoid
def sigmoid (z):
return 1 / ( 1 + np . exp(-z))
# Sigmoid Derivatives
def sigmoid_derivatives (a):
return a * (1 - a)
def forward_propagation (W, b, X):
# W, B: 一列为一组数据
Z = np . dot(W . T, X) + b
A = sigmoid(Z)
return A3 . 定义损失函数。
def loss_function (y, a):
# one sample
return -y * np . log(a) - (1 - y) * np . log(1 - a)
def Loss_Fn (Y, A):
# all samples (1, 209)
m = Y . shape[1]
# log(0)会遇到报错情况
epsilon = 1e-5
J = (1 / m) * np . sum(-Y * np . log(A + epsilon) - (1 - Y) * np . log(1 - A + epsilon))
return J4 . 梯度下降,定义向后传播。
def backward_propagation (Y, A, X):
# eg: A: 1 * m, Y: 1 * m X: 3 * m
m = A . shape[1]
dL_dZ = A - Y
dL_dW = (1 / m) * np . dot(X, (A - Y) . T)
dL_dB = (1 / m) * np . sum(A - Y)
return dL_dW, dL_dB
5 . 训练模型。(这只是一层模型,如果有很多层的话,详看 两层NN demo[12])。
def train (X, Y, alpha, iterations):
# ......
# hyperparameters
# alpha = 0.005
# iterations = 2000
# 1. Initializing parameters - 目标
W, b = initialize_parameters(input_nums, output_nums)
J_arr = []
# 4. iterations: 2,3,4
for i in range(iterations): # 不停训练
# 2. Forward Propagation 向前传播
A = forward_propagation(W, b, X)
# 3. Backward Propagation 向后传播,梯度下降
dL_dW, dL_dB = backward_propagation(Y, A, X)
W -= alpha * dL_dW # 类似下山步伐和方向
b -= alpha * dL_dB # 类似下山步伐和方向
return W, b, J_arr总结
上述,我只是简单介绍了一点有关NN模型的基础知识,实际上有关神经网络的知识还很多。本次分享的初衷是通过一些对模型基础的理解 + TensorFlow.js,前端同学也可以玩玩机器学习。
在我们的业务场景里,常见算法对业务赋能的场景,例如在出读阅卷中的图像识别 (eg: 对于一张试卷结构和标志点等识别)。
参考资料
[1]机器学习、深度学习和强化学习的关系和区别是什么? - 知乎: https://www.zhihu.com/question/279973545/answer/588124593
[2]DEEP REINFORCEMENT LEARNING.pdf: https://arxiv.org/pdf/1810.06339.pdf
[3]代码: https://github.com/Linjiayu6/Tensorflow.js-LinearRegression/blob/master/src/tensorflow.js
[4]过往实验例子: https://github.com/Linjiayu6/Machine-Learning-Practice/tree/master/Regression/logistic_regression
[5]高斯分布 / 正态分布: https://zh.wikipedia.org/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83
[6]伯努利分布: https://zh.wikipedia.org/wiki/%E4%BC%AF%E5%8A%AA%E5%88%A9%E5%88%86%E5%B8%83
[7]最大似然估计: https://zhuanlan.zhihu.com/p/26614750
[8]逻辑回归demo,感兴趣可以去看看: https://github.com/Linjiayu6/Deep-Learning/blob/master/coursera/L1_Neural%20Networks%20and%20Deep%20Learning/W2__Logistic%20Regression%20demo.ipynb
[9]学习资料: 3blue1brown-深度学习(英文搬运)_哔哩哔哩_bilibili: https://www.bilibili.com/video/BV1Et411779N?p=2
[10]偏移量增加的意义: https://www.zhihu.com/question/68247574
[11]代码: 用NN识别一只: https://github.com/Linjiayu6/Deep-Learning/blob/master/coursera/L1_Neural%20Networks%20and%20Deep%20Learning/W2__Logistic%20Regression%20with%20a%20Neural%20Network%20mindset.ipynb
[12]两层NN demo: https://github.com/Linjiayu6/Deep-Learning/blob/master/coursera/L1_Neural%20Networks%20and%20Deep%20Learning/W5__2-Layer__Deep%20Neural%20Network%20for%20Image%20Classification%20-%20Application.ipynb