435次阅读 | 发布于2年以前

简介

D3.js[1] 是一个基于 web 标准的 JS 可视化库，它借助 SVG、Canvas 和 HTML 进行数据可视化。在数据可视化中，我们很多时候会使用图来表达数据中所蕴含的信息，图方便让我们清晰的理清各个节点之间的联系，快速提取有用信息。而图布局算法可以使散乱的信息 (信息多以点线的关系承载) 通过一种清晰的方式呈现出来，符合相应的美学标准。

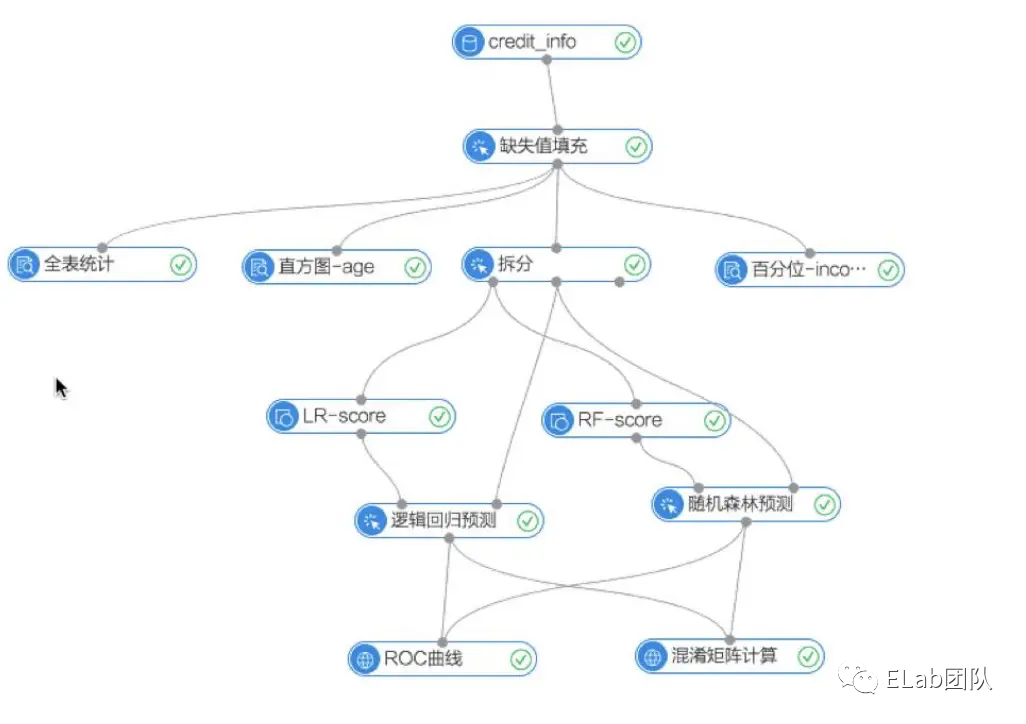
不同的图布局[2]也有不同的应用场景，例如树形布局 / Dagre布局，它是一个有向无环图，具有的拓扑性质，可以用作流程表达的场景。

同心圆布局，图分析的场景中通常是将节点先按照度数排序，度数最大的节点会排列在最中心的位置，越往外度数越小，整体成同心圆形式排列。

力导布局，通过节点之间的互斥力，减少重叠，但是在有限的空间内避免所有节点不重叠目前还是无解的。我们今天讲一下，简单的力导布局的实现。建立在物理理论基础上，将节点模拟为原子，通过原子之间作用力的相互影响，最终达到平衡状态，这就是力导向图[3]。

思路

整体可以拆解为 2 个实体和 1 个作用因子：节点、线、力。d3-force的实现与传统的 FR 算法思路一样，可以分成三个部分组成，先计算节点间的互斥力，再计算连接点的吸引力，得出最终的作用力，得到每个节点的速度。使用模拟退火的衰减方案，达到稳定。

https://jsfiddle.net/smallstars/h8y6e031/51/

d3-force原理

节点处理

初始化导入节点

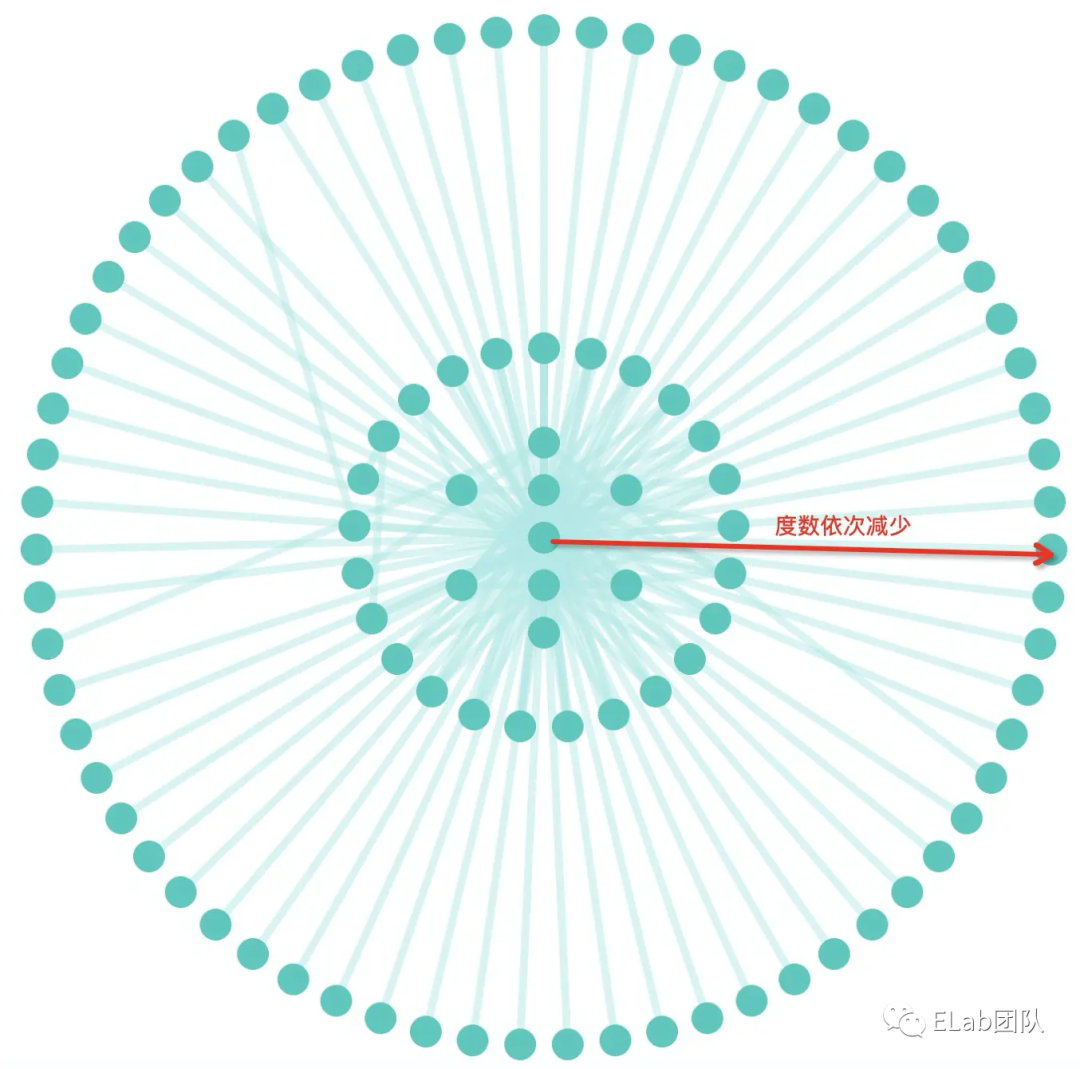
将节点导入 d3 中，需要对节点进行预处理，按照一定的半径和角度进行环绕。

// d3-force/simulation.js
var initialRadius = 10,
    initialAngle = Math.PI * (3 - Math.sqrt(5));

function initializeNodes() {
    for (var i = 0, n = nodes.length, node; i < n; ++i) {
      node = nodes[i], node.index = i;
      if (node.fx != null) node.x = node.fx;
      if (node.fy != null) node.y = node.fy;
      // 初始位置
      if (isNaN(node.x) || isNaN(node.y)) {
        var radius = initialRadius * Math.sqrt(0.5 + i), angle = i * initialAngle;
        node.x = radius * Math.cos(angle);
        node.y = radius * Math.sin(angle);
      }
      // vx, vy为 x, y 的速度
      if (isNaN(node.vx) || isNaN(node.vy)) {
        node.vx = node.vy = 0;
      }
    }
}

建立节点四叉树

四叉树（quad-tree）

这里采取四叉树的结构原因是方便做碰撞检测, 四叉树是从根节点开始，每一个节点下面最多有四个子树的数据结构。通常我们把一部分二维空间细分为四象限，每一个节点存储相应的象限信息。

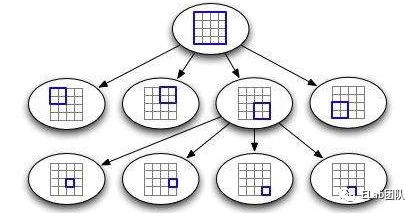
遍历导入所有节点数据，求出最小值 ,最大值 , 最小值 ,最大值，将与进行增幅，满足 ,。2的倍数满足四叉树在一维上对半分的特征。我们在添加节点的时候，总共会有下面 4 种情况：

四叉树为空，节点添加为根节点。
当前查询节点为索引节点且添加处范围矩阵为空，直接添加。
当前查询节点为真实节点且添加节点坐标相等且无数组索引，建立数组索引，再次划分该矩阵，直到查询节点与添加节点处于不同矩阵。
当前查询节点为真实节点且添加节点坐标相等且有数组索引，直接下挂。

// d3-force/collide.js
for (var k = 0; k < iterations; ++k) {
  // 调用 d3-quadtree 进行add
  tree = quadtree(nodes, x, y).visitAfter(prepare);
  for (i = 0; i < n; ++i) {
    node = nodes[i];
    ri = radii[node.index], ri2 = ri * ri;
    xi = node.x + node.vx;
    yi = node.y + node.vy;
    tree.visit(apply);
  }
}


// d3-quadtree/add.js
function add(tree, x, y, d) {
  if (isNaN(x) || isNaN(y)) return tree; // ignore invalid points

  var parent,
      node = tree._root,
      leaf = {data: d},
      // 象限坐标
      x0 = tree._x0,
      y0 = tree._y0,
      x1 = tree._x1,
      y1 = tree._y1,
      xm,
      ym,
      xp,
      yp,
      right,
      bottom,
      i,
      j;

  // case1: If the tree is empty, initialize the root as a leaf.
  if (!node) return tree._root = leaf, tree;

  // 类似二分，自上向下搜索
  // Find the existing leaf for the new point, or add it.
  while (node.length) {
    if (right = x >= (xm = (x0 + x1) / 2)) x0 = xm; else x1 = xm;
    if (bottom = y >= (ym = (y0 + y1) / 2)) y0 = ym; else y1 = ym;
    // case2: 判断当前添加节点所在象限是否为空
    if (parent = node, !(node = node[i = bottom << 1 | right])) return parent[i] = leaf, tree;
  }

  // case4: 添加节点是否与父节点重合
  // Is the new point is exactly coincident with the existing point?
  xp = +tree._x.call(null, node.data);
  yp = +tree._y.call(null, node.data);
  if (x === xp && y === yp) return leaf.next = node, parent ? parent[i] = leaf : tree._root = leaf, tree;

  // case3: 不停分割，直到处于不同象限
  // Otherwise, split the leaf node until the old and new point are separated.
  do {
    parent = parent ? parent[i] = new Array(4) : tree._root = new Array(4);
    if (right = x >= (xm = (x0 + x1) / 2)) x0 = xm; else x1 = xm;
    if (bottom = y >= (ym = (y0 + y1) / 2)) y0 = ym; else y1 = ym;
  } while ((i = bottom << 1 | right) === (j = (yp >= ym) << 1 | (xp >= xm)));
  return parent[j] = node, parent[i] = leaf, tree;
}

斥力的优化求解

节点间的斥力优化关键为电荷斥力[4]求解优化，最基本的一个节点所受的力，需要与其他所有节点进行计算求和，复杂度为。

整合受力

而四叉树结构与 Barnes-Hut[5] 近似，复杂度可降为。当前节点所受周围点的斥力进行整合处理，大小由 Barnes-Hut 近似精度 (默认值为 ) 决定，最后根据 Velocity Verlet[6] 对速度进行求解。

象限面积，节点(node)与象限点(quad)形成的面积

  // d3-force/manyBody.js
  var distanceMin2 = 1,
      distanceMax2 = Infinity,
      theta2 = 0.81;

  function apply(quad, x1, _, x2) {
    if (!quad.value) return true;

    var x = quad.x - node.x,
        y = quad.y - node.y,
        w = x2 - x1,
        l = x * x + y * y;

    // Barnes-Hut成立
    // 如何点非常近，冲突的时候随机方向
    if (w * w / theta2 < l) {
      if (l < distanceMax2) {
        if (x === 0) x = jiggle(random), l += x * x;
        if (y === 0) y = jiggle(random), l += y * y;
        if (l < distanceMin2) l = Math.sqrt(distanceMin2 * l);
        node.vx += x * quad.value * alpha / l;
        node.vy += y * quad.value * alpha / l;
      }
      return true;
    }

    // Barnes-Hut不成立且 quad 有节点
    else if (quad.length || l >= distanceMax2) return;

    // 排除自身对自身影响，还可以继续向下遍历
    if (quad.data !== node || quad.next) {
      if (x === 0) x = jiggle(random), l += x * x;
      if (y === 0) y = jiggle(random), l += y * y;
      if (l < distanceMin2) l = Math.sqrt(distanceMin2 * l);
    }

    do if (quad.data !== node) {
      w = strengths[quad.data.index] * alpha / l;
      node.vx += x * w;
      node.vy += y * w;
    } while (quad = quad.next);
  }

节点连线的处理

先初始化连线，计算节点的度和每一条边对起始节点度(source/target degree)的占比，使，alpha为阻尼系数，默认边长度(distance)为30，默认弹簧劲度(strength)为，减少度大节点的引力，提高稳定性。计算连线两边的引力，最终推导出速度的变化。

同理可得出

// d3-force/link.js
function force(alpha) {
    for (var k = 0, n = links.length; k < iterations; ++k) {
      for (var i = 0, link, source, target, x, y, l, b; i < n; ++i) {
        link = links[i], source = link.source, target = link.target;
        x = target.x + target.vx - source.x - source.vx || jiggle(random);
        y = target.y + target.vy - source.y - source.vy || jiggle(random);
        l = Math.sqrt(x * x + y * y);
        l = (l - distances[i]) / l * alpha * strengths[i];
        x *= l, y *= l;
        target.vx -= x * (b = bias[i]);
        target.vy -= y * b;
        source.vx += x * (b = 1 - b);
        source.vy += y * b;
      }
    }
}

布局的形成

通过不断的迭代运算，每次运算都可以看做一步，通过模拟退火的衰减方案最后达到稳定状态。

 // d3-force/simulation.js
 var simulation,
    alpha = 1,
    alphaMin = 0.001,
    // alpha衰减率
    alphaDecay = 1 - Math.pow(alphaMin, 1 / 300),
    alphaTarget = 0,
    // 速度衰减
    velocityDecay = 0.6,
    stepper = timer(step),
    // tick事件与end事件
    event = dispatch("tick", "end");

function step() {
  tick();
  event.call("tick", simulation);
  if (alpha < alphaMin) {
    stepper.stop();
    event.call("end", simulation);
  }
}

function tick() {
  // alpha不断衰减
  alpha += (alphaTarget - alpha) * alphaDecay;

  // 不停迭代
  forces.each(function(force) {
    force(alpha);
  });

  // 速度转化为距离改变
  for (i = 0; i < n; ++i) {
    node = nodes[i];
    if (node.fx == null) node.x += node.vx *= velocityDecay;
    // 具有fx，说明当前节点被控制，不需要受到力的影响，速度置为0
    else node.x = node.fx, node.vx = 0;
    if (node.fy == null) node.y += node.vy *= velocityDecay;
    else node.y = node.fy, node.vy = 0;
  }
}

实战示例

Demo:

React-d3js[7]

代码:

https://github.com/SmaIIstars/react-demo/blob/master/src/pages/d3-force/index.tsx

遇见的问题

1 . Svg 中绘制复杂内容

可以使用 foreignObject 节点进行绘制，在 foreignObject 中可以编写 XML 命名空间的元素。

2 . 节点迭代次数过多，导致页面卡顿

通常初次生成图布局的时候，需要一个过渡动画，在模拟退火的过程中，节点、线会不断的移动。监听数据的变化，使用 React.memo 和 useCallback 减少不必要的运算。

3 . 节点间重叠，相互遮盖

增大排斥力，增常线段长度，增加碰撞体积。但是在有限的空间内，仍然无法完全避免重叠的问题。

4 . 节点过多，超出画布

使用设备的宽高作为画布，对内容进行缩放和拖拽，让用户可以查看到所有内容。

参考

GitHub - d3/d3-force: Force-directed graph layout using velocity Verlet integration.[8]
D3.js(Data-Driver Documents)力导向图理论知识[9]

参考资料

[1]D3.js: https://github.com/d3/d3

[2]图布局: https://segmentfault.com/a/1190000039054038

[3]力导向图: https://observablehq.com/@sandravizmad/force-directed-layout

[4]电荷斥力: https://bytedance.feishu.cn/docs/doccnyBnKUxyMSdw74Tws6lavfd#8M5j10

[5]Barnes-Hut: https://bytedance.feishu.cn/docs/doccnyBnKUxyMSdw74Tws6lavfd#yeVWli

[6]Velocity Verlet: https://bytedance.feishu.cn/docs/doccnyBnKUxyMSdw74Tws6lavfd#lfo9UK

[7]React-d3js: http://demo.smallstars.top/demo/d3-force

[8]GitHub - d3/d3-force: Force-directed graph layout using velocity Verlet integration.: https://github.com/d3/d3-force

[9]D3.js(Data-Driver Documents)力导向图理论知识: https://bytedance.feishu.cn/docs/doccnyBnKUxyMSdw74Tws6lavfd#WmTLGZ

深入理解 D3.js 可视化库之力导向图原理与实现

简介

思路