算法 | 多叉树先序输出所有路径 - 哈喽比特

484次阅读 | 发布于2年以前

1、背景

最近在做一个方法调用链扫描的工具，需要根据方法的调用关系输出所有方法的调用链路。方法调用关系的扫描结果以 json 格式表示时数据结构如下。咋一看可能不熟悉，但是用图把关系绘制出来之后，很明显可以发现这是一个多叉树数据结构：

{
    "A": ["B", "G"],
    "B": ["C", "D"],
    "G": ["D", "E", "F"],
    "D": ["J", "K"],
    "E": ["K"],
    "F": []
}

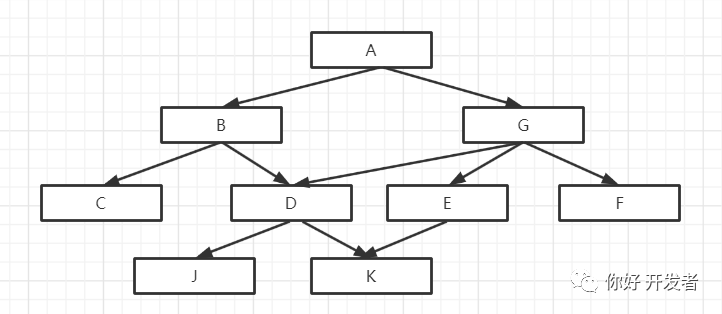
多叉树的应用场景非常多，比如文件系统就是多叉树结构。如果用图来展示的话，方法调用链的数据结构如下图所示。

显然，跟普通多叉树相比这种树还存在一个结点拥有多个父结点的情形。实际应用场景中的情形可能更加复杂，比如递归调用；比如某个方法在一个树中作为根结点，但是在另一个树中又作为子结点等等。

2、算法过程

如果仅仅是多叉树进行遍历，本身并不困难。通常，为了追求更好的效率，我们会直接使用非递归形式的遍历算法。虽然有些语言对尾递归做了优化，但是非递归是更好的选择。这种算法又分为 DFS（深度优先搜索算法） 和 BFS（广度优先搜索算法） 两种。

这里的一个问题在于，当我们遍历完一个父结点的所有子结点的时候需要从路径列表中删除根结点。这里我用了一个技巧，即在将根结点的子结点插入到遍历的列表的时候末尾追加一个“标记”。当遇到这个标记的时候就表示根结点可以从列表中弹出了。

示例程序如下，

public class TreeVisitTest {

    private static final Split split = new Split("", Arrays.asList());

    public static void main(String...args) {
        // 构建一棵多叉树
        Node f = new Node("F", Arrays.asList());
        Node e = new Node("E", Arrays.asList());
        Node d = new Node("D", Arrays.asList());
        Node b = new Node("B", Arrays.asList(f, e));
        Node c = new Node("C", Arrays.asList(d));
        Node h = new Node("H", Arrays.asList(d));
        Node i = new Node("I", Arrays.asList());
        Node a = new Node("A", Arrays.asList(b, c));
        Node g = new Node("G", Arrays.asList(h, i));
        Node s = new Node("S", Arrays.asList(a, g));

        // 对树进行先序遍历
        List<List<Node>> links = new ArrayList<>();
        List<Node> link = new ArrayList<>();
        List<Node> nodes = new ArrayList<>();
        nodes.add(s);
        while (!nodes.isEmpty()) {
            Node node = nodes.remove(0);
            if (node == split) {
                // 将路径插入到最终结果集中
                links.add(new ArrayList<>(link));
                // 弹出根结点
                link.remove(link.size()-1);
                continue;
            }
            link.add(node);
            // 先序遍历插头部，屏障插入到子结点的末尾
            nodes.add(0, split);
            nodes.addAll(0, node.children);
        }

        // 输出结果
        output(links);
    }

    /** 输出结果 */
    private static void output(List<List<Node>> links) {
        for (List<Node> link : links) {
            for (int i=0, len=link.size(); i<len; i++) {
                System.out.print(link.get(i));
                if (i != len-1) {
                    System.out.print("->");
                }
            }
            System.out.println();
        }
    }

    /** 用于标记末尾的分界点 */
    private static class Split extends Node {
        public Split(String name, List<Node> children) {
            super(name, children);
        }
    }

    /** 树的结点的数据结构 */
    private static class Node {

        private String name;

        /** 当前结点的所有子结点 */
        private List<Node> children;

        public Node(String name, List<Node> children) {
            this.name = name;
            this.children = children;
        }

        @Override
        public String toString() {
            return name;
        }
    }
}

输出的结果如下所示，

S->A->B->F
S->A->B->E
S->A->B
S->A->C->D
S->A->C
S->A
S->G->H->D
S->G->H
S->G->I
S->G
S

这里用了非递归的先序遍历的基本结构，用 link 表示当前剩余的路径。这里是将走过的所有结点插入到 link 中，不过当到了根结点的时候，遇到了“屏障”才弹出根结点。需要注意的是，这里的将路径添加到 links 之前需要先使用 Collection 再包装一层。

总结

实现过程并不复杂，但是这种多叉树结构的算法我遇到的还是挺多的。实际在开发过程中遇到的情况要远比上面复杂得多。不过，我们只有掌握了上述基本的结构，才能在面对更加复杂的情况的时候随机应变。