存储系统中内存索引结构的选择

radix tree

随着最近几十年来服务器主存容量的增加，即使是大型的事务数据库也能把索引全部放到主存中，当索引数据都在内存中时，索引的性能也就越来越重要。

传统的数据库系统比如mysql一般用B+树作为自己的索引，B+树能够有效减少磁盘IO次数，支持范围查询，但在纯内存环境下，它的性能表现并不太好，特别是B+树是通过key的比较来找节点的，当比较结果产生分支预测失败时，会引起CPU stall。

哈希表是另外一个流行的内存数据结构，和查找树O(logn)的查找时间相比，哈希表只有O(1)的查找时间。尽管如此，哈希表有两个缺陷，一个是哈希表不能支持范围查询，二是哈希表的rehash非常慢可能会造成严重的性能抖动。如果说业务不需要支持范围查询又容量恒定的话，哈希表是最快的索引结构。

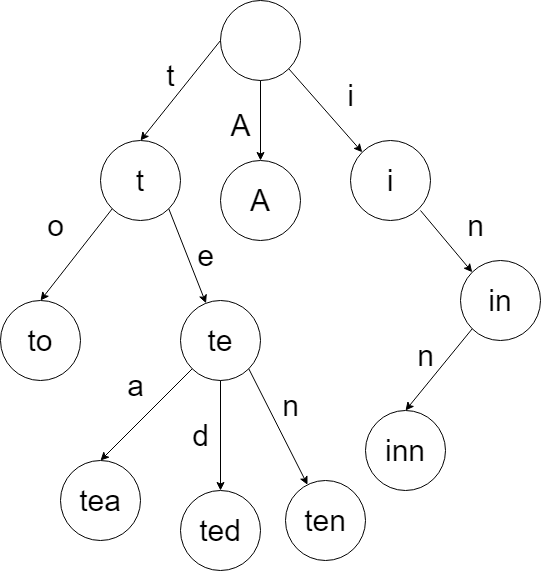
第三种数据结构被称为radix tree，或者前缀树，trie等。和二叉树不同，key不会直接保存在节点中，而是由节点在树中的位置决定。radix tree把一个完整的key转变成了字符的序列，每个节点都对应一个特定的字符，每个字符都有可能指向任意一个字符。在radix tree中查找一个key就像查字典一样。从根节点开始每个字符都可以找到一个对应的节点，依次查找key的所有字符就找到了key对应的叶子结点。

由于这种构建方式，radix tree有很多有吸引力的特性使它和基于比较的搜索树完全不同：

1. radix tree的高度和搜索的复杂度和key的长度有关，和包含的元素数无关
2. radix tree没有rebalance
3. 中间节点不需要保存key，叶子结点的路径就是key

radix tree有两种类型的节点：内部节点，通过key的一部分指向其他节点；叶子节点，存储了key所对应的数据。内部节点一般用一个数组表示，在遍历过程中，key的一部分作为数组的索引，这样不用任何的比较就能找到下一个节点。部分key的比特数也就是参数span，对于radix tree的性能非常重要，当key的总长度和span确定后，树的高度也就确定了。

在数据库系统中，基于比较的搜索树是非常常见的索引结构，可以简单比较一下radix tree的高度和平衡二叉树的比较次数。平衡二叉树每次比较只能排除1/2的数据，而radix tree在span=8时，每次能排除255/256的数据，所以平衡二叉树的高度会更高。

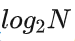
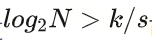
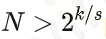
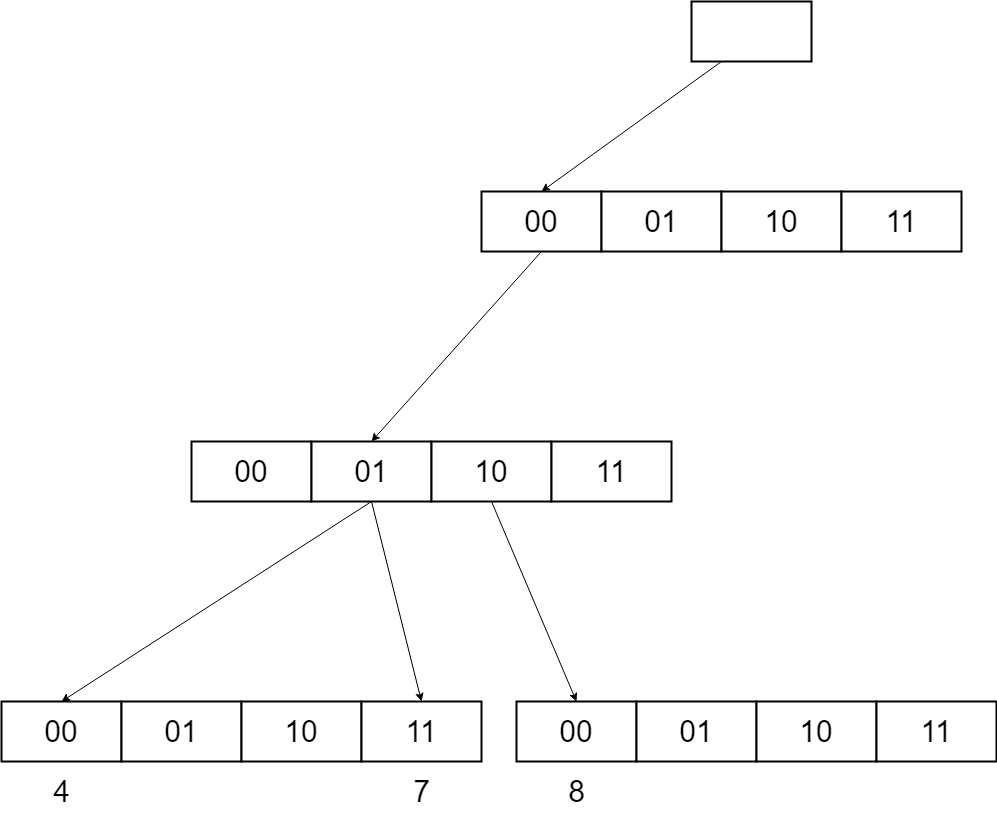
我们可以通过一个简单的公式分析一下，假设key有k位，那么在radix tree里查找一个key需要k/s次，也就是树的高度。平衡二叉树在同样元素数据下的高度，假设元素个数是N，那么平衡二叉树的高度是 ，radix tree的高度是k/s，通过 可以看出当 时，平衡二叉树的高度就大于radix tree的高度了。也就是说radix tree的key是64位，span是8位时，超过256个元素的集合用radix tree的高度就会低于平衡二叉树。

再考虑到key的比较时间的话，一个比较大的span通常会使radix tree比传统的搜索树快很多。但span也不是越大越好，大的span在key非常稀疏的场景下会引起空间的浪费。比如下面这个例子，key有6位，span是2位，最多可以存64个key，假设现在有3个key 4、7、8，二进制表示分别是000100、000111、001000，实际用的空间是16个指针128字节，平均每个key用了42字节；当有4、5、6、7、8、9、10、11， 8个key时，实际使用的内存还是128字节，但平均每个key用的内存降到了16字节。

为了解决这些问题，V Leis提出了一种自适应节点的radix tree，Adaptive Radix Tree简称ART。它在水平方向和垂直方向都做了压缩，以及用了SIMD指令来加速节点的查找。

优化1-节点压缩

定长的数组非常浪费内存，而频繁的resize非常影响性能，所以ART用了4种大小内部节点类型，Node4、Node16、Node48、Node256。理论上来说内部节点只要能通过key的一部分找到正确的子节点就可以。

1.Node4

Node4是最小的节点类型，可以保存最多4个子指针，key和子指针都被保存在长度为4的数组中。

struct Node4
{
    Node          header;
    unsigned char child_keys[4];
    Node*         child_ptrs[4];
};

Node4* findChild(char c, Node4* node) 
{
    for (int i = 0; i < node->child_count; i++)
    {
        if (n->child_keys[i] == byte)
        {
            return &n->child_ptrs[i];
        }
    }
    return NULL;
}

2.Node16

Node16用来保存5到16个子指针，跟Node4一样，key和子指针保存在两个数组相同的位置，但是数组大小是16。在支持SSE2的CPU上可以用SIMD指令来做并行加速。

struct Node16 
{
    Node          header;
    unsigned char child_keys[16];
    Node*         child_ptrs[16];
    unsigned char num_children;
};

Node* findChild(char byte, Node16* node)
{
    __m128i results = _mm_cmpeq_epi8(_mm_set1_epi8(byte), _mm_loadu_si128((__m128i*)(&node->child_keys[0])));
    int mask = (1 << node->num_children) - 1;
    int bitfield = _mm_movemask_epi8(results) &amp; mask;
    if (bitfield == 0)
    {
        return NULL;
    }
    return &node->child_ptrs[__builtin_ctz(bitfield)];

3.Node48

Node48用来保存17到48个子节点，Node48不会再直接保存key的内容，而是用key直接在长256的数组里查找孩子的下标，然后在长48的数组里找到子指针，Node48和Node256直接用span就可以直接找到对应的子节点。

struct Node48
{
    Node          header;
    unsigned char child_ptr_indexs[256];
    Node*         child_ptrs[48];
};

Node* findChild(char byte, Node48* node)
{
    Node48* n = reinterpret_cast<Node48*>(node);
    int index = n->child_ptr_indexs[byte];
    if (index == 0)
    {
        return NULL;
    }
    return &n->child_ptrs[index - 1];
}

4.Node256

Node256是最大的节点，用来保存49到256个子指针。它把指针放在了长256的数组里，用key可以直接索引到指针。

struct Node256
{
    Node    header;
    Node*   child_ptrs[256];
};

Node* findChild(char byte, Node256* node)
{
    Node256* n = reinterpret_cast<Node256*>(node);
    return &n->child_ptrs[byte];
}

用了这四种内部节点后，radix tree的状态就变成了下图，在key稀疏的场景下能有效的节省内存。

优化2-路径压缩

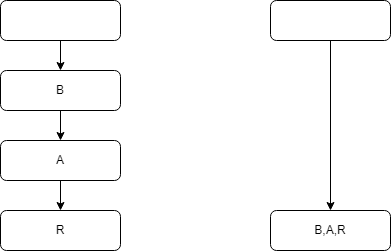
比如我们现在有一棵树BAR,BAZ，B只有一个子节点A，A有两个节点R,Z，那其实BA合并为一个节点就可以了，只需要增加一个vector保存BA的序列。

优化3-慢展开

慢展开的优化思路其实和上面的路径压缩是一样，只不过场景不一样，当最下面的子节点只有一个时，可以把路径上所有的序列都合并到叶子节点中。

性能

现在的服务器上内存越来越大，但CPU的cache仍然很小，所以对于索引来说节省内存对于提升性能来说尤其重要。对于radix tree来说，key在稀疏场景下有很大的内存浪费，而且会让cache miss更加严重。ART通过自适应节点和路径压缩优化了这些问题，使得不管在key非常稀疏还是密集的场景下，索引的性能都很优秀。作者在论文中推理了每个key占用的内存最多是52个字节，而在密集的场景下最好能做到8.1字节，而且在实际应用场景中，密集的key是更常见的。

作者也做了很多试验来对比ART和其他索引的性能，通过图表可以看出在不同的key数量下，ART的查询性能都比其他索引要好，只有哈希表和它在一个数量级。

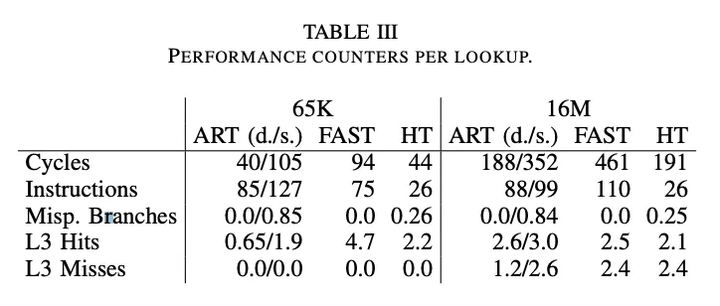
然后作者又分析了导致性能差异的原因，在1600万key的时候，哈希表，FAST和稀疏ART的cache miss是差不多的。而在密集场景下，ART的内存对于CPU cache更加友好，可以减少一半的cache miss，所以性能要比其他的索引好。在6万key的时候，查询性能主要受指令数和分支预测失败影响，密集场景下ART基本没有分支预测失败，稀疏场景下ART每次lookup有0.85次分支预测失败，而且在密集场景下Node256的查询需要的指令数更少，所以ART在密集场景下要比稀疏场景好不少。

本着严谨的原则，我们也实现了ART，并把它和红黑树，哈希表做了一些性能对比，红黑树用的就是std::map，哈希表用的std::unordered_map。测试用了一个自己实现的内存benchmark，key是uint64，value是一个8字节的指针，1000万key的规模，在顺序和随机模式下分别测试了红黑树，哈希表和ART的性能表现。

顺序插入1000万key顺序查找1000万key随机插入1000万key随机查找1000万keyART0.12us 29B0.08us0.42us 40B0.21ushash0.16us 48B0.04us0.71us 48B0.26usrb-tree0.31us 66B0.19us1.63us 66B0.96us从我们自己的测试结果发现密集场景和稀疏场景，每个key的内存占用差距似乎没有想象中大。最后发现原来是内存的字节序引起的，如果直接把key 1,2转换成字节序是[1,0,0,0,0,0,0,0] [2,0,0,0,0,0,0,0]，如果按照这个字节序列插入的话，那前缀压缩几乎就没有效果了，如下图

所以在树在初始化的时候要根据机器确定下字节序的问题。

通用的ART为了解决不定长的key的读取问题会在叶子结点存储整个key，比如key BAR是key BARR的前缀，但他们是两个key。但在我们的业务场景下，key是定长的，所以在叶子节点是不用保存key的，只要保证查询路径是固定字节数就可以了。经过这些优化，在密集场景下可以将每个key的内存占用优化到8B。

顺序插入1000万key顺序查找1000万key随机插入1000万key随机查找1000万keyART0.11us 8B0.05us0.53us 51B0.06ushash0.16us 48B0.04us0.71us 48B0.26usrb-tree0.31us 66B0.19us1.63us 66B0.96us总结

我们分析了存储系统通常用的一些内存索引，介绍了最近比较流行的radix tree的变种ART，它有着radix tree的优点，并且很大程度上优化了radix tree的缺点。

通过作者的性能分析可以看出在现代的服务器上，cache miss和分支预测失败等因素对于索引的性能影响非常大，ART在这些方面做了很多优化，并且利用了一些SIMD的指令来加速查询。我们自己的测试也发现ART在不通场景下都优于其他类型的索引，只有哈希表跟它性能差不多，但哈希表只能支持点查询。

我们的业务系统在单机存储引擎上用的就是哈希表，但当系统架构从原地写模式转变为追加写以后，碎片化就非常严重，每个用户连续的1M块可能每个4k都是不通的物理存储位置，所以哈希表就不再适用于这个场景了。ART最大的好处就是它的数据都是顺序存储的，所以在范围查询上相比哈希表优势就非常大了。当然最后，最合适的才是最好的，还是要根据业务场景来选择最合适的索引。