如何实现一个Canvas渲染引擎(二):Graphics类
1 前言
本文将会补充Graphics类支持的所有图形,一些简单的图形,将会使用比较短的篇幅来介绍,重点将会放在曲线等复杂图形的绘制上。鉴于我们已经讲过了矩形的绘制,所以本文将会从圆开始。
2 简单图形
2.1 圆
我们会用一个Circle类来代表一个圆,注意,是一个完整的圆,而不是圆弧。
export class Circle extends Shape {
public x: number
public y: number
public radius: number
public readonly type = ShapeType.Circle
constructor(x = 0, y = 0, radius = 0) {
super()
this.x = x
this.y = y
this.radius = radius
}
public contains(point: Point): boolean {
return true
}
}绘制圆的代码如下
if (shape instanceof Circle) {
const circle = shape
const { x, y, radius } = circle
ctx.beginPath()
ctx.arc(x, y, radius, 0, 2 * Math.PI)
ctx.closePath()
if (fillStyle.visible) {
ctx.globalAlpha = fillStyle.alpha * this.worldAlpha
ctx.fill()
}
if (lineStyle.visible) {
ctx.globalAlpha = lineStyle.alpha * this.worldAlpha
ctx.stroke()
}
}2.2 椭圆
用Ellipse类来表示椭圆,注意,是一个完整的椭圆,而不是一部分
export class Ellipse extends Shape {
public x: number
public y: number
public radiusX: number
public radiusY: number
public readonly type = ShapeType.Ellipse
constructor(x = 0, y = 0, radiusX = 0, radiusY = 0) {
super()
this.x = x
this.y = y
this.radiusX = radiusX
this.radiusY = radiusY
}
public contains(point: Point): boolean {
return true
}
}绘制椭圆的代码如下
if (shape instanceof Ellipse) {
const ellipse = shape
const { x, y, radiusX, radiusY } = ellipse
ctx.beginPath()
ctx.ellipse(x, y, radiusX, radiusY, 0, 0, Math.PI * 2)
if (fillStyle.visible) {
ctx.globalAlpha = fillStyle.alpha * this.worldAlpha
ctx.fill()
}
if (lineStyle.visible) {
ctx.globalAlpha = lineStyle.alpha * this.worldAlpha
ctx.stroke()
}
}2.3 圆角矩形
我们将会用RoundedRectangle类来表示圆角矩形,圆角矩形就是4个四分之一圆+4条线段
export class RoundedRectangle extends Shape {
public x: number
public y: number
public width: number
public height: number
public radius: number
public readonly type = ShapeType.RoundedRectangle
constructor(x = 0, y = 0, width = 0, height = 0, radius = 20) {
super()
this.x = x
this.y = y
this.width = width
this.height = height
const r = Math.min(width, height) / 2
this.radius = radius > r ? r : radius
}
public contains(point: Point): boolean {
return true
}
}绘制圆角矩形的代码如下
if (shape instanceof RoundedRectangle) {
const roundedRectangle = shape
const { x, y, width, height, radius } = roundedRectangle
ctx.beginPath()
ctx.moveTo(x + radius, y)
ctx.arc(x + radius, y + radius, radius, Math.PI * 1.5, Math.PI, true)
ctx.lineTo(x, y + height - radius)
ctx.arc(
x + radius,
y + height - radius,
radius,
Math.PI,
Math.PI / 2,
true
)
ctx.lineTo(x + width - radius, y + height)
ctx.arc(
x + width - radius,
y + height - radius,
radius,
Math.PI / 2,
0,
true
)
ctx.lineTo(x + width, y + radius)
ctx.arc(x + width - radius, y + radius, radius, 0, Math.PI * 1.5, true)
ctx.closePath()
if (fillStyle.visible) {
ctx.globalAlpha = fillStyle.alpha * this.worldAlpha
ctx.fill()
}
if (lineStyle.visible) {
ctx.globalAlpha = lineStyle.alpha * this.worldAlpha
ctx.stroke()
}
}2.4 多边形
我们将会用Polygon类来表示一个多边形
export class Polygon extends Shape {
public points: number[] // 多边形由多个点构成,points数组每2个元素代表一个顶点的坐标
public closeStroke = false
public readonly type = ShapeType.Polygon
constructor(points: number[] = []) {
super()
this.points = points
}
public contains(point: Point): boolean {
return true
}
}points数组每两个元素代表一对(x,y),也就是多边形的一个顶点
绘制多边形的代码如下
if (shape instanceof Polygon) {
const polygon = shape
const { points, closeStroke } = polygon
ctx.beginPath()
ctx.moveTo(points[0], points[1])
for (let i = 2; i < points.length; i += 2) {
ctx.lineTo(points[i], points[i + 1])
}
if (closeStroke) {
ctx.closePath()
}
if (fillStyle.visible) {
ctx.globalAlpha = fillStyle.alpha * this.worldAlpha
ctx.fill()
}
if (lineStyle.visible) {
ctx.globalAlpha = lineStyle.alpha * this.worldAlpha
ctx.stroke()
}
}2.5 整体效果
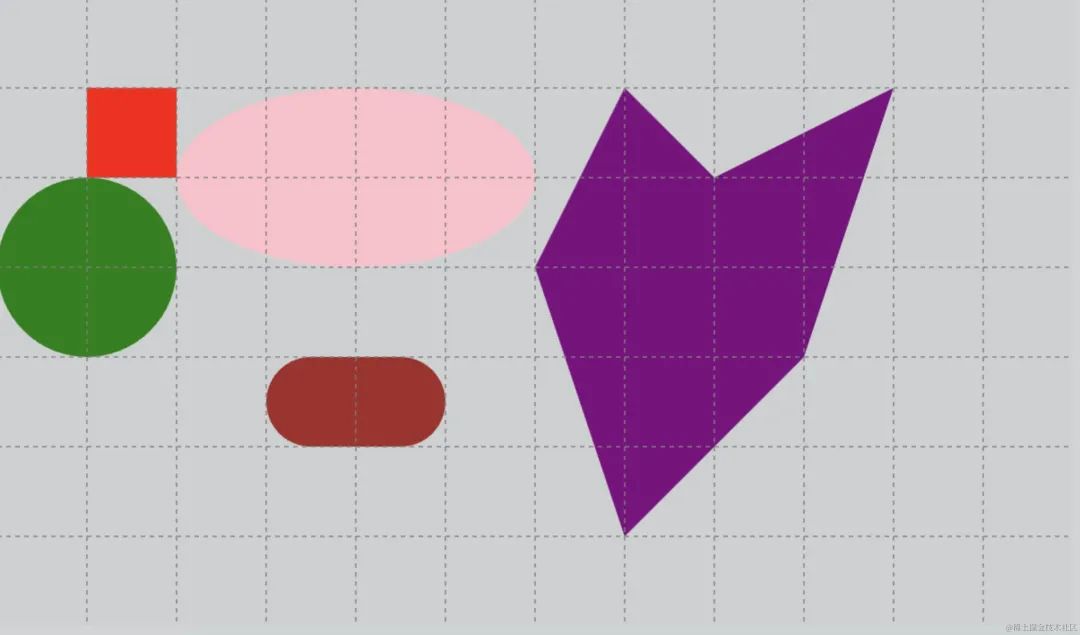
测试一下所有简单图形的效果
2.5.1 代码
const graphic = new Graphics()
.beginFill('red')
.drawRect(100, 100, 100, 100)
.beginFill('green')
.drawCircle(100, 300, 100)
.beginFill('pink')
.drawEllipse(400, 200, 200, 100)
.beginFill('brown')
.drawRoundedRect(300, 400, 200, 100, 100)
.beginFill('purple')
.drawPolygon([
600, 300, 700, 100, 800, 200, 1000, 100, 900, 400, 700, 600
])
app.stage.addChild(graphic)2.5.2 效果
「灰色的背景和虚线辅助线是另加的,大家可以忽略」
code sandbox地址
3 复杂图形
3.1 如何在这个渲染引擎中实现曲线
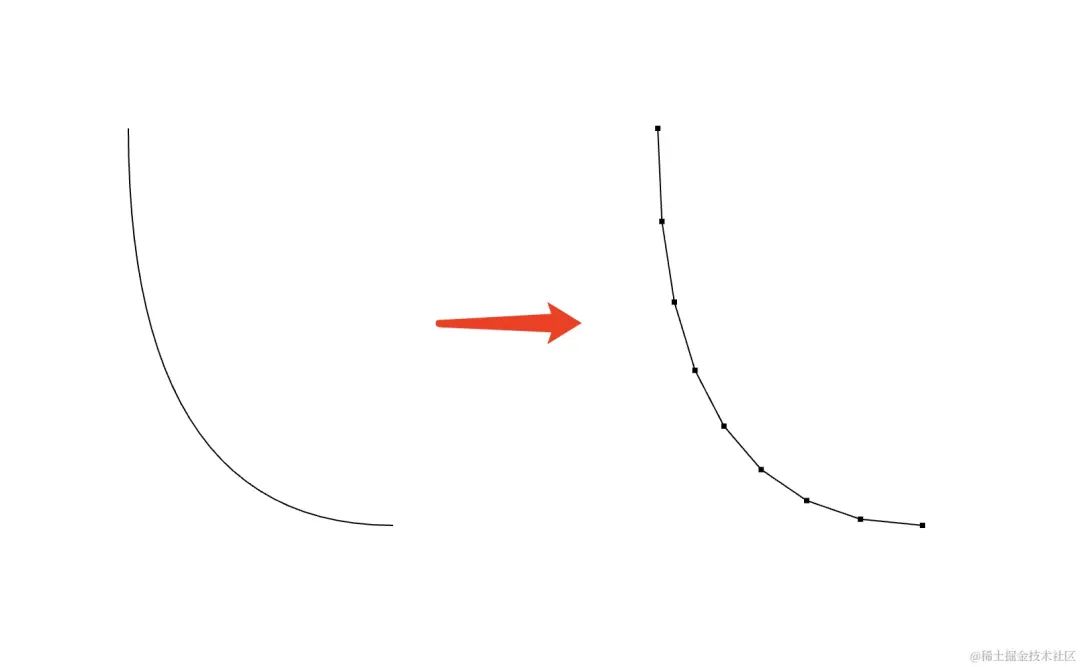
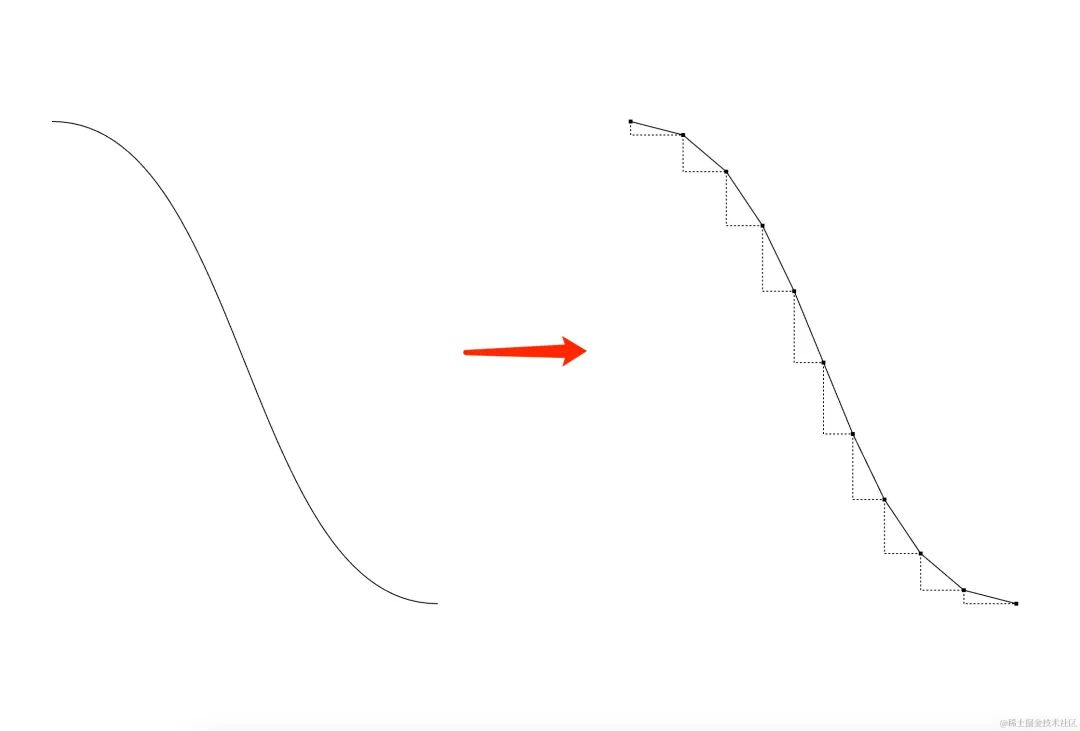
首先明确一点,除了第2节提到的那些带有曲线的图形(椭圆、圆等),其他任何带有曲线的图形,都会用多边形来近似,比如二阶贝塞尔曲线的近似:
这是为了后面的碰撞检测功能作准备,碰撞检测功能做的事情就是:判断一个点是否在一个封闭的图形的内部;我们只能判断一个点是否在一个封闭的直边多边形内部(后续的文章会解释),如果是一个曲边多边形,那么我们就无从下手了。
3.2 二阶贝塞尔曲线
我们用3个点来表示一条二阶贝塞尔曲线,这3个点分别是P0P_0P0、P1P_1P1和P2P_2P2,他们分别代表着这条二阶贝塞尔曲线的起始点、控制点、终点。如果对贝塞尔曲线不太熟悉,可以去看看这几篇文章
深入理解贝塞尔曲线
如何理解并应用贝塞尔曲线
我们说了,从第3节开始讲述的所有曲线,都将用多边形来近似,那么现在问题来了,我们要怎么用多边形来近似贝塞尔曲线呢?
3.2.1 把t均分成n份
我们首先要在贝塞尔曲线上采样一系列的点
贝塞尔曲线是一个xxx和yyy关于ttt的参数方程,t∈[0,1]t\in[0,1]t∈[0,1],要在贝塞尔曲线上采样多个点,可以把[0,1][0,1][0,1]这个区间分成n份,这样我们就得到了n个ttt值,然后把这些ttt值代入贝塞尔曲线的参数方程,我们就可以得到n个位于贝塞尔曲线上的点,然后把这些点连起来,就得到了一条近似的贝塞尔曲线。
3.2.2 采样多少个点?
n的值如何求出呢?
我们会根据贝塞尔曲线的长度,来决定这个n到底有多大,如果曲线很长,那么n就会很大,意味着我们要用更多的点来近似这条贝塞尔曲线;如果曲线很短,那么n会很小,意味着我们会用比较少的点来近似这条贝塞尔曲线。
3.2.3 求贝塞尔曲线的长度
求一条曲线的长度?想必大家心中已经有了答案了,那就是
定积分。定积分的应用有很多,除了最经典的求曲边梯形的面积,还有求旋转体的体积,求曲线的弧长,这里我们要用到的就是求曲线的弧长
我们要做的事情,就是得出贝塞尔曲线的弧长的积分表达式(对哪个函数进行积分以及积分区间),在做这件事情之前,我们先来简单回顾一下如何得出一些简单的量的积分表达式。
「如果不想看这些纯数学问题,可以直接跳到3.2.4代码实现。」
3.2.3.1 量和一份的概念
求定积分的时候,我们要把要求的量拆解成无限多份,然后得出其中的一份的表达式,得到了这个一份的表达式之后,我们也就得到了积分表达式。
3.2.3.2 求曲边梯形的面积
以f(x)=x2f(x)=x^2f(x)=x2这个函数为例,这个函数的图像是这样的: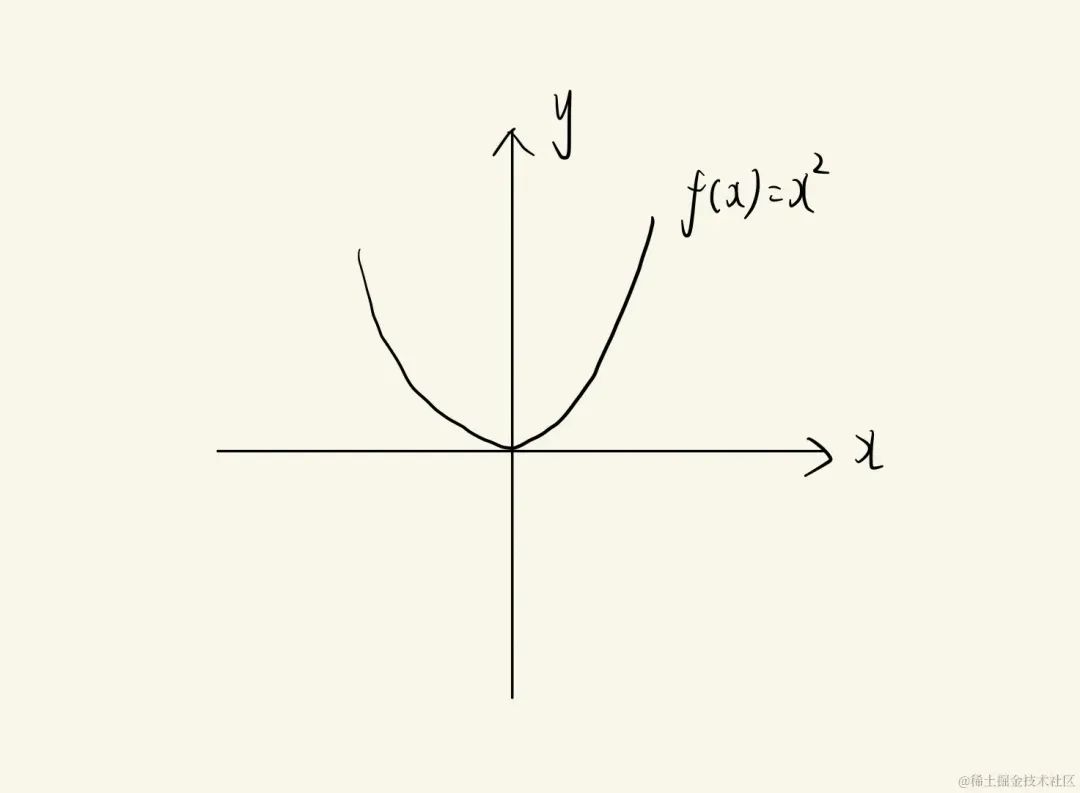
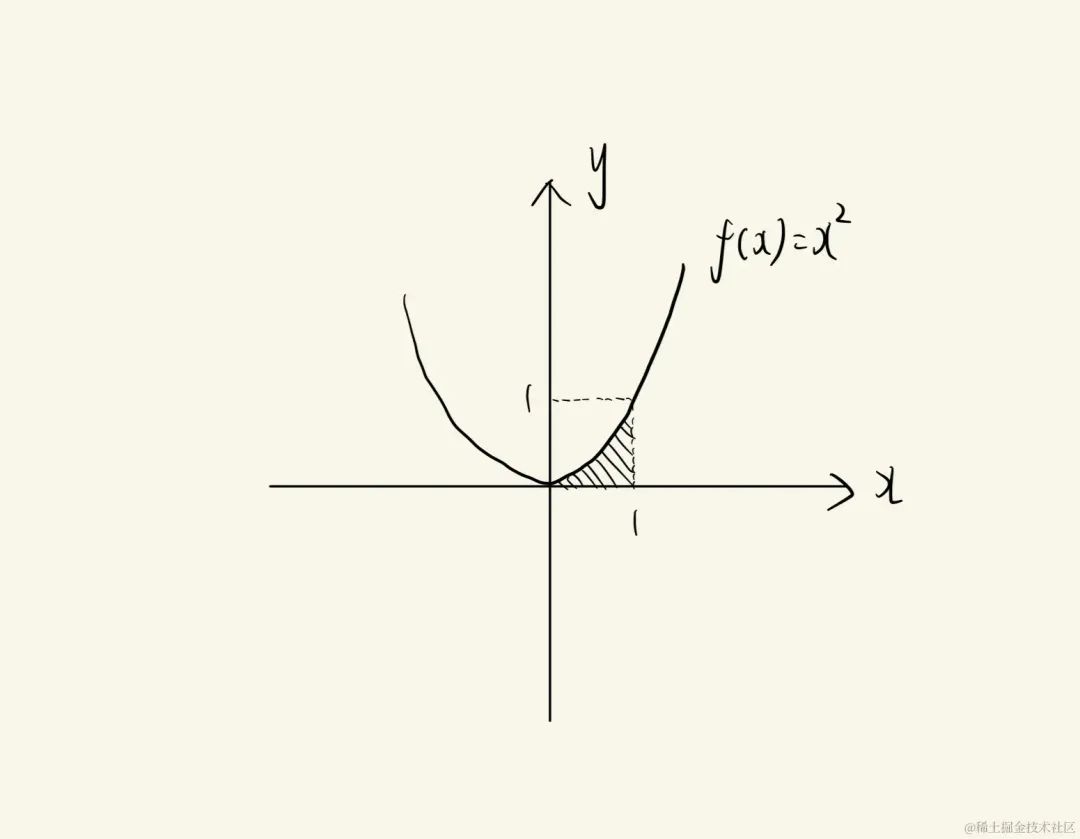
量是阴影部分面积,我们先将其放大(放大到特别大),然后取其中的一小份(假设无限小),如下: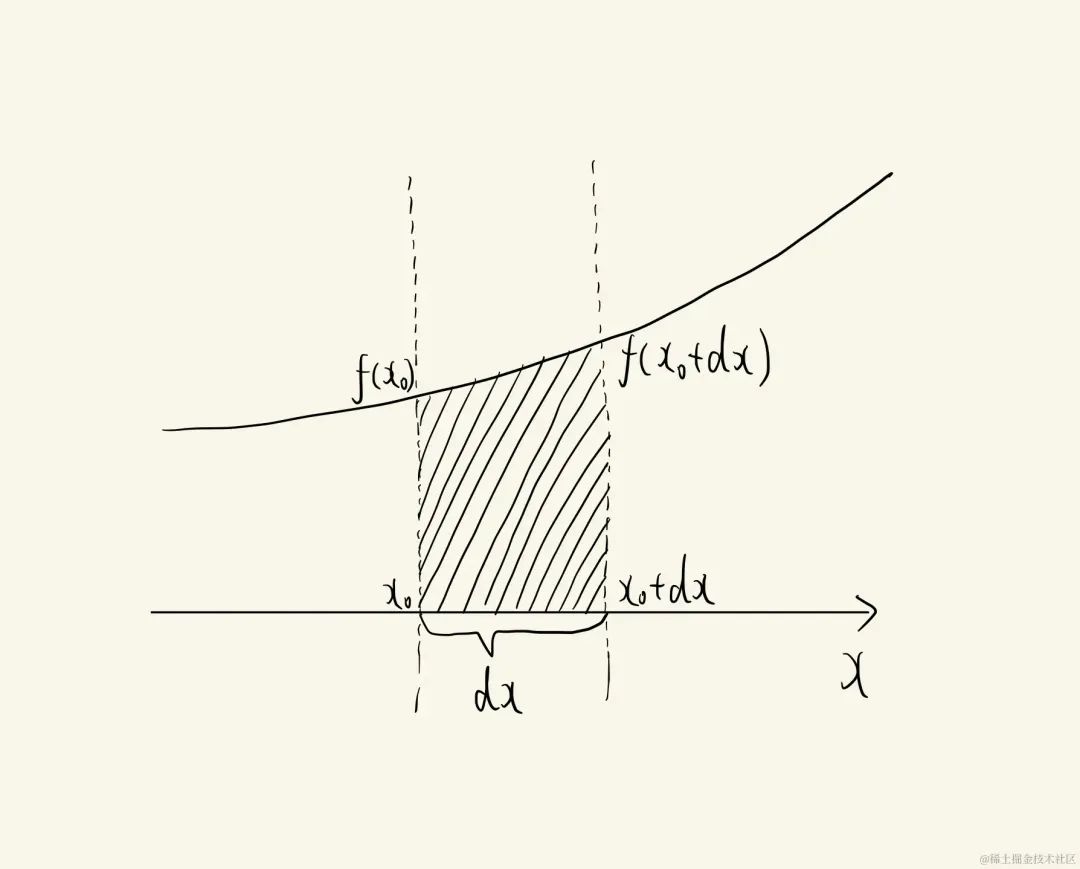
一份,它的宽度为dxdxdx(一个无穷小的值),无穷多个这样的一份加起来,就等于我们要求的量(面积),我们只需要表达出这个一份,就可以得出积分表达式。
可以看到,这个一份(阴影区域的面积)SSS可以表达为:S=f(x0)×dxS=f(x_0)\times dxS=f(x0)×dx (其实取[x0,x0+dx][x_0,x_0+dx][x0,x0+dx]之间的任意一个点都行,这里取了左边的端点),所以我们的积分表达式是:∫01f(x)dx\int_0^1 f(x)dx∫01f(x)dx,即∫01x2dx\int_0^1 x^2dx∫01x2dx
接下来的事情就比较简单了,根据「微积分基本定理(牛顿-莱布尼兹公式)」,我们需要得到f(x)f(x)f(x)的原函数,也就是13x3\frac{1}{3}x^331x3,把000和111代进去减一下,就得到了结果,结果为13\frac{1}{3}31,所以f(x)=x2f(x)=x^2f(x)=x2在x∈[0,1]x\in[0,1]x∈[0,1]区间的面积是13\frac{1}{3}31
3.2.3.3 求曲线的弧长
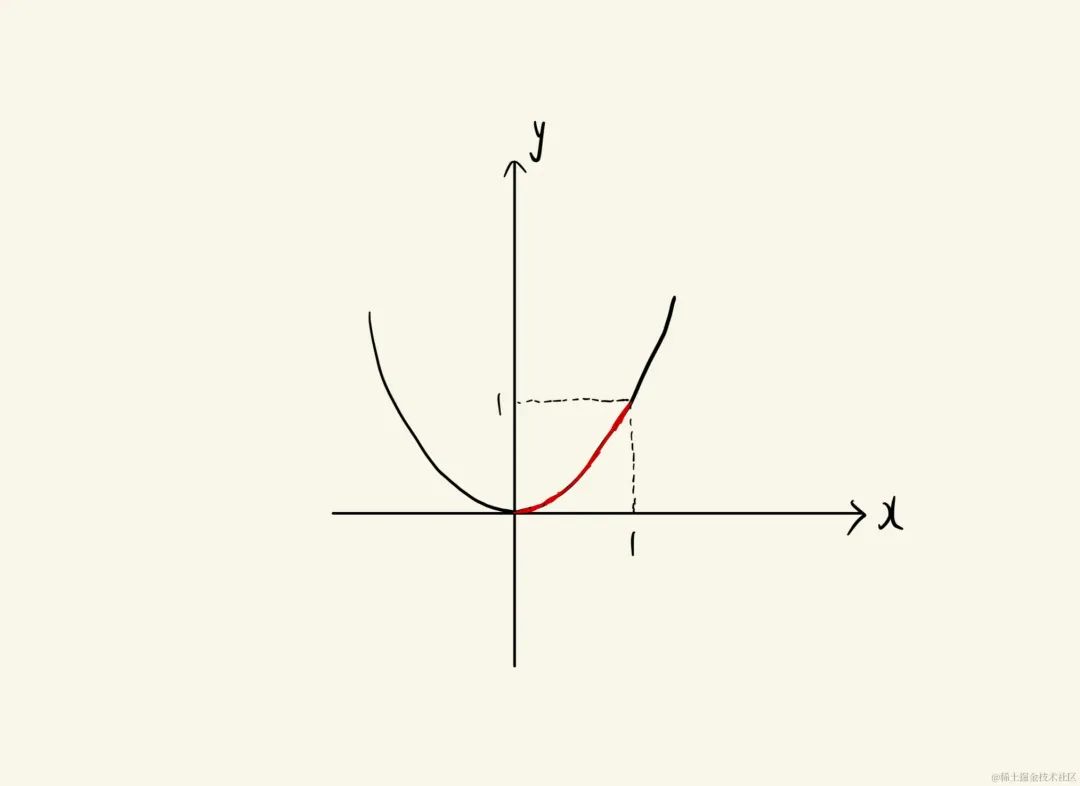
这里还是以f(x)=x2f(x)=x^2f(x)=x2这个函数为例,假设我们要求这个函数在x∈[0,1]x\in[0,1]x∈[0,1]这一段的弧长,如下图(红色部分):
我们要求的量是红色曲线的弧长,按照惯例,我们先将图像放大到很大,然后再截取一小段(假设无限小):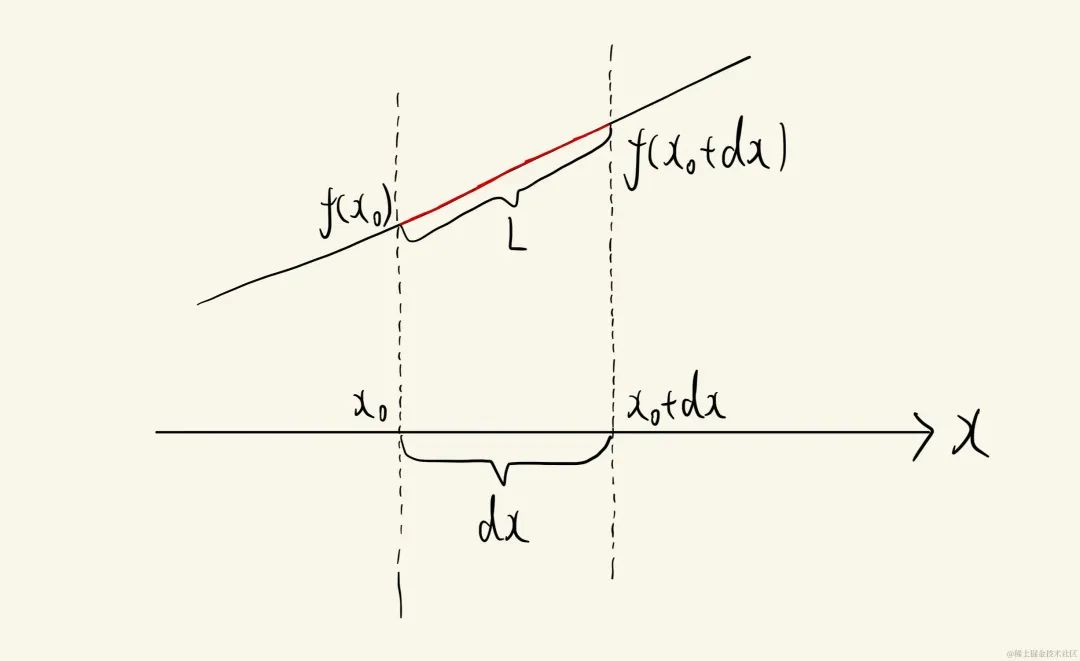
一份,我们截取的这个区间的长度依然为dxdxdx,当dxdxdx趋近于无穷小时,我们可以近似地把这个红色的线段看作「直线」,所以,我们可以用「勾股定理」来求出这个红色线段的长度LLL: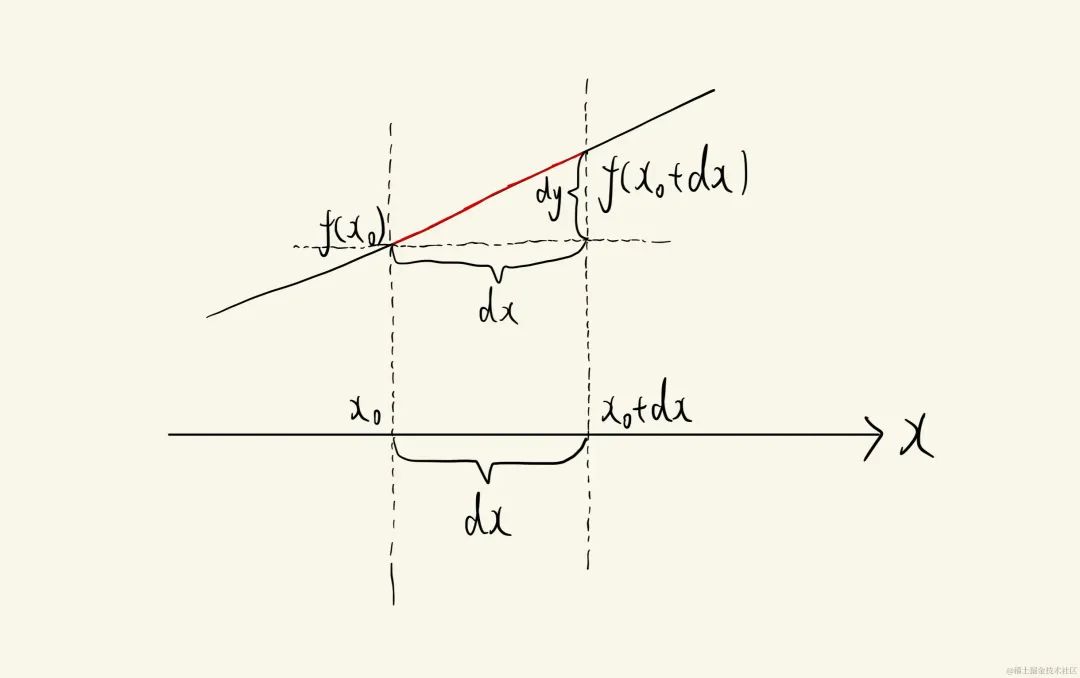
可以得到:
L=(dx)2+(dy)2=(dx)2+(f′(x0)×dx)2L=\sqrt{(dx)^2+(dy)^2}=\sqrt{(dx)^2+(f'(x_0)\times dx)^2}L=(dx)2+(dy)2=(dx)2+(f′(x0)×dx)2
将dxdxdx提出来,可以得到:
L=1+(f′(x0))2×dxL=\sqrt{1+(f'(x_0))^2} \times dxL=1+(f′(x0))2×dx
所以我们的积分表达式是:∫011+(f′(x))2dx\int_0^1\sqrt{1+(f'(x))^2}dx∫011+(f′(x))2dx,即∫011+4x2dx\int_0^1\sqrt{1+4x^2}dx∫011+4x2dx
接下来还是运用「牛顿-莱布尼兹公式」,但是这个根号让我们的积分变的十分困难,如果能去掉这个根号那将是绝杀,可惜去不得,不过好在1+4x2\sqrt{1+4x^2}1+4x2是一种常见的积分类型,即∫x2+a2dx\int\sqrt{x^2+a^2}dx∫x2+a2dx型,如果大家不知道怎么积,可以去看看这篇文章:zhuanlan.zhihu.com/p/349530983,在这里我们直接套公式,得到∫1+4x2dx=x24x2+1+14ln∣2x+4x2+1∣+C\int\sqrt{1+4x^2}dx=\frac{x}{2}\sqrt{4x^2+1}+\frac{1}{4}\ln\bigg\lvert2x+\sqrt{4x^2+1}\bigg\rvert+C∫1+4x2dx=2x4x2+1+41ln2x+4x2+1+C,将000和111代入,得到∫011+4x2dx=52+14ln(2+5)\int_0^1\sqrt{1+4x^2}dx=\frac{\sqrt{5}}{2}+\frac{1}{4}\ln(2+\sqrt{5})∫011+4x2dx=25+41ln(2+5),所以函数f(x)=x2f(x)=x^2f(x)=x2的曲线在x∈[0,1]x\in[0,1]x∈[0,1]这一段的弧长为52+14ln(2+5)≈1.4789\frac{\sqrt{5}}{2}+\frac{1}{4}\ln(2+\sqrt{5})\approx1.478925+41ln(2+5)≈1.4789
3.2.3.4 求二阶贝塞尔曲线的弧长
我们用3个点来表示一条二阶贝塞尔曲线,这3个点分别是P0P_0P0、P1P_1P1和P2P_2P2,他们分别代表着这条二阶贝塞尔曲线的起始点、控制点、终点。
二阶贝塞尔曲线并不是经典的yyy对xxx的函数,而是一个yyy对ttt以及xxx对ttt的函数,它只能用参数方程来表示,我们用P0xP_0xP0x和P0yP_0yP0y来表示P0P_0P0的xxx坐标和yyy坐标,用P1xP_1xP1x和P1yP_1yP1y来表示P1P_1P1的xxx坐标和yyy坐标,用P2xP_2xP2x和P2yP_2yP2y来表示P2P_2P2的xxx坐标和yyy坐标,那么二阶贝塞尔曲线的参数方程为:
{x=(1−t)2×P0x+2t(1−t)×P1x+t2×P2xy=(1−t)2×P0y+2t(1−t)×P1y+t2×P2y\begin{cases} x=(1-t)^2\times P_0x + 2t(1-t) \times P_1x + t^2 \times P_2x \\ y=(1-t)^2\times P_0y + 2t(1-t) \times P_1y + t^2 \times P_2y \end{cases}{x=(1−t)2×P0x+2t(1−t)×P1x+t2×P2xy=(1−t)2×P0y+2t(1−t)×P1y+t2×P2y
我们依然会采用前面求曲线的弧长的方式来求贝塞尔曲线的弧长,以起始点P0P_0P0=(1,1),P1P_1P1=(1,2),P2P_2P2=(2,2)的贝塞尔曲线为例,它的图像是这样的: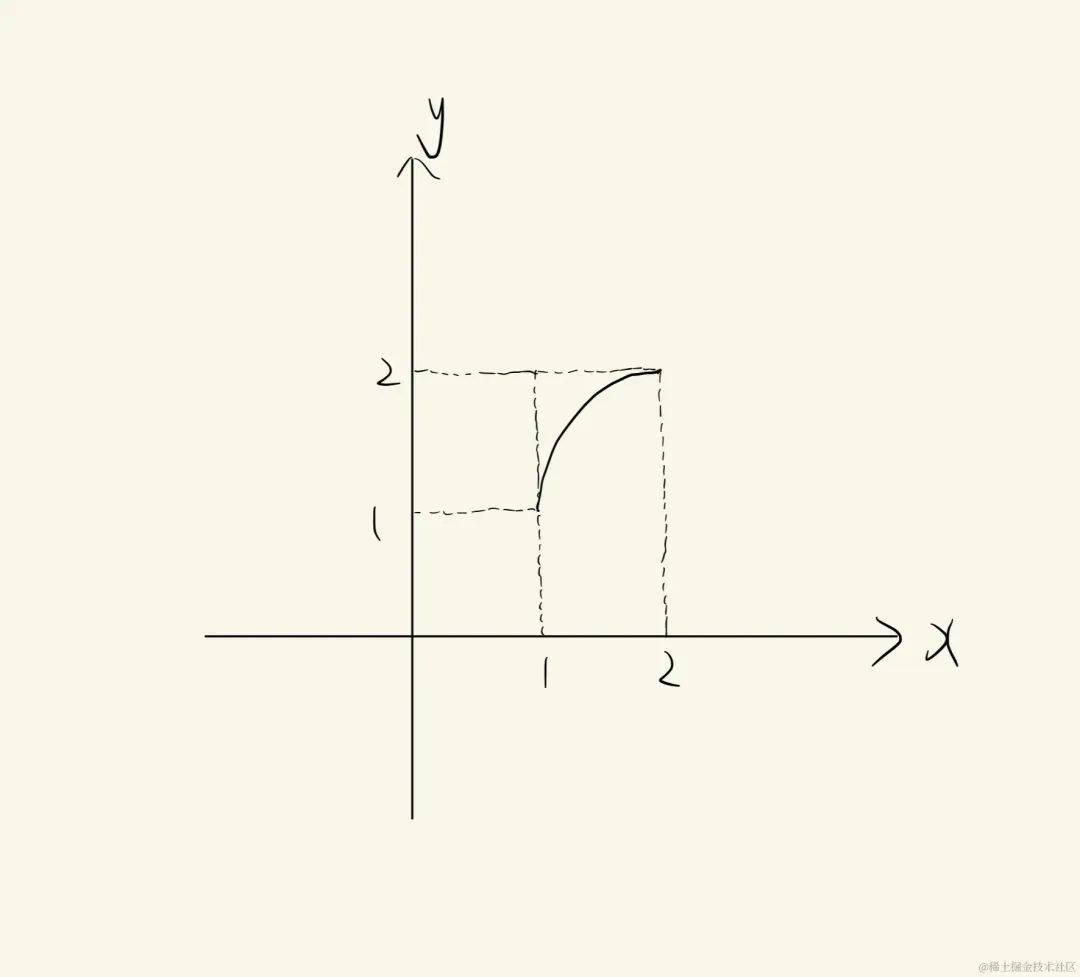
我们要求的量是整条贝塞尔曲线的长度,依然是按照惯例,我们先将图像放大到很大,然后再截取一小段(假设无限小):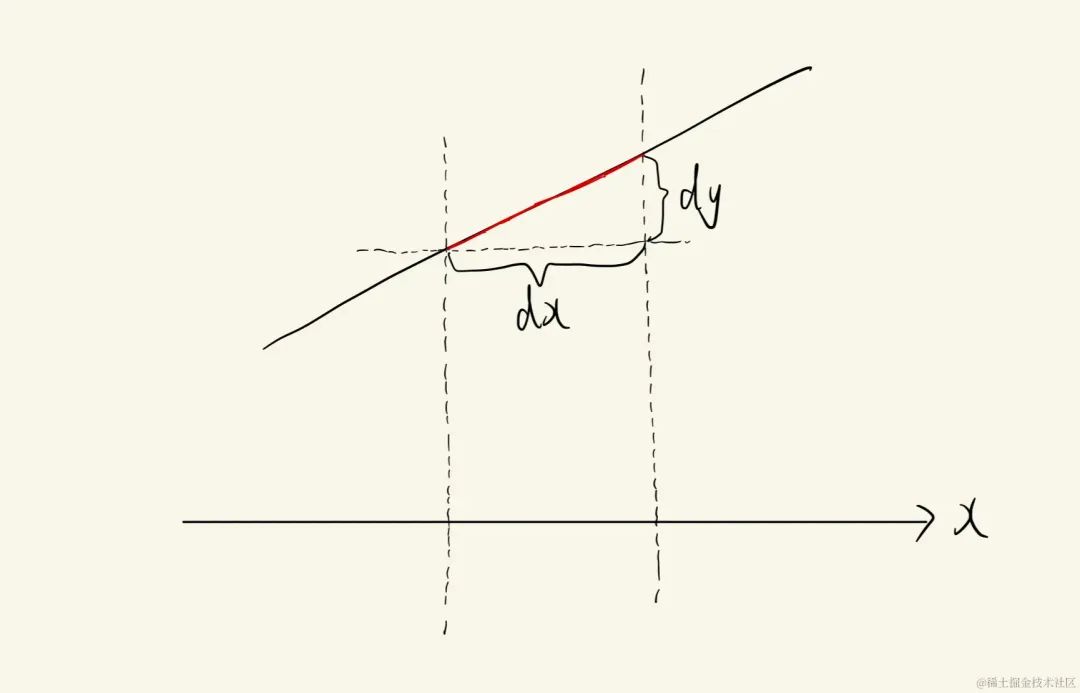
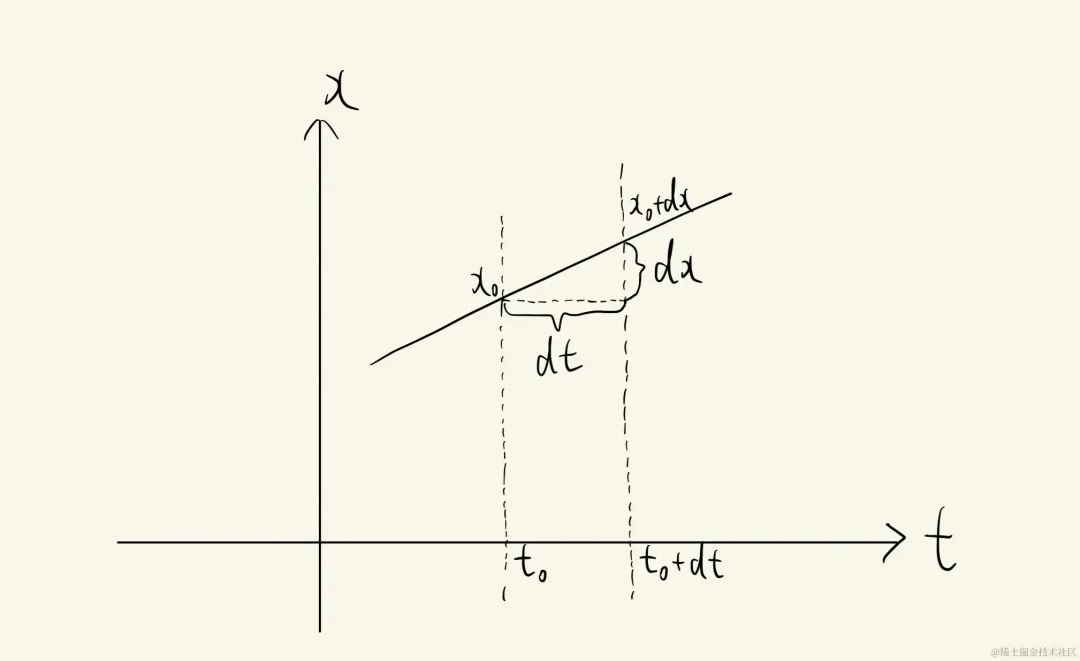
一份,dxdxdx是这条线段在xxx轴方向上的长度,dydydy是这条线段在yyy轴方向上的长度,当dxdxdx和dydydy趋近于无穷小时,可以把红色的线段看作一条直线,所以,我们依然可以使用勾股定理,得出L=(dx)2+(dy)2L=\sqrt{(dx)^2+(dy)^2}L=(dx)2+(dy)2。但是,到这里还没有结束,我们要对ttt进行积分,而不是对xxx和yyy进行积分,所以这里我们还要得出dxdxdx和dydydy对于dtdtdt的表达式;由于xxx对ttt的函数和yyy对ttt的函数的形式是一样的,所以我们只需要求出dxdxdx对dtdtdt的表达式也就得到了dydydy对dtdtdt的表达式。
dxdxdx就是xxx对ttt的函数在ttt的变化量为dtdtdt(dtdtdt趋近于无穷小)时,xxx的变化量。如下:
dtdtdt是一个无穷小量,这个时候,我们可以通过导数(即斜率)得出dxdt=x0′\frac{dx}{dt}=x_0'dtdx=x0′,x0′x_0'x0′是xxx对ttt的函数在t=t0t=t_0t=t0处的导数,将dtdtdt乘到右边,我们有:dx=x0′×dtdx=x_0' \times dtdx=x0′×dt。通过同样的方法,我们可以得到:dy=y0′×dtdy=y_0' \times dtdy=y0′×dt。所以我们要求的一份L=(dx)2+(dy)2=(x0′×dt)2+(y0′×dt)2=(x0′)2+(y0′)2×dtL=\sqrt{(dx)^2+(dy)^2}=\sqrt{(x_0' \times dt)^2+(y_0' \times dt)^2}=\sqrt{(x_0')^2+(y_0')^2} \times dtL=(dx)2+(dy)2=(x0′×dt)2+(y0′×dt)2=(x0′)2+(y0′)2×dt,所以,我们的积分表达式是:∫01(x′)2+(y′)2dt\int_0^1\sqrt{(x')^2+(y')^2}dt∫01(x′)2+(y′)2dt,接下来就是求函数(x′)2+(y′)2\sqrt{(x')^2+(y')^2}(x′)2+(y′)2的不定积分了。
根据贝塞尔曲线的参数方程,有:
{x′=2(P0x−2P1x+P2x)t−2(P0x−P1x)y′=2(P0y−2P1y+P2y)t−2(P0y−P1y)\begin{cases} x'=2(P_0x-2P_1x+P_2x)t-2(P_0x-P_1x) \\ y'=2(P_0y-2P_1y+P_2y)t-2(P_0y-P_1y) \end{cases}{x′=2(P0x−2P1x+P2x)t−2(P0x−P1x)y′=2(P0y−2P1y+P2y)t−2(P0y−P1y)
为了简化这个公式,我们把一些常数挪到一起,用另一些常数代替,令ax=2(P0x−2P1x+P2x)a_x=2(P_0x-2P_1x+P_2x)ax=2(P0x−2P1x+P2x),bx=−2(P0x−P1x)b_x=-2(P_0x-P_1x)bx=−2(P0x−P1x),ay=2(P0y−2P1y+P2y)a_y=2(P_0y-2P_1y+P_2y)ay=2(P0y−2P1y+P2y),by=−2(P0y−P1y)b_y=-2(P_0y-P_1y)by=−2(P0y−P1y),所以:
{x′=axt+bxy′=ayt+by\begin{cases} x'=a_xt+b_x \\ y'=a_yt+b_y \end{cases}{x′=axt+bxy′=ayt+by
所以(x′)2+(y′)2=(ax2+ay2)t2+2(axbx+ayby)t+bx2+by2\sqrt{(x')^2+(y')^2}=\sqrt{(a_x^2+a_y^2)t^2+2(a_xb_x+a_yb_y)t+b_x^2+b_y^2}(x′)2+(y′)2=(ax2+ay2)t2+2(axbx+ayby)t+bx2+by2
为了简化这个式子,我们再次将常量挪到一起,用另一些常量替换,令A=ax2+ay2A=a_x^2+a_y^2A=ax2+ay2,B=2(axbx+ayby)B=2(a_xb_x+a_yb_y)B=2(axbx+ayby),C=bx2+by2C=b_x^2+b_y^2C=bx2+by2,
所以(x′)2+(y′)2=At2+Bt+C\sqrt{(x')^2+(y')^2}=\sqrt{At^2+Bt+C}(x′)2+(y′)2=At2+Bt+C
接下来我们依然会使用换元法,来求解这个不定积分,我们会用换元法将其化解成∫x2+a2dx\int\sqrt{x^2+a^2}dx∫x2+a2dx型不定积分,然后套公式得出结果,如果大家不知道怎么求∫x2+a2dx\int\sqrt{x^2+a^2}dx∫x2+a2dx型不定积分,可以去看看这篇文章:zhuanlan.zhihu.com/p/349530983…
首先,At2+Bt+CAt^2+Bt+CAt2+Bt+C是两个平方量的和((x′)2(x')^2(x′)2和(y′)2(y')^2(y′)2),所以At2+Bt+C>=0At^2+Bt+C>=0At2+Bt+C>=0,根据一元二次方程解的个数的判断公式,我们有B2−4AC<=0B^2-4AC<=0B2−4AC<=0
接下来就是开始换元了:
∫At2+Bt+Cdt\int\sqrt{At^2+Bt+C}dt∫At2+Bt+Cdt
=∫1A×A×At2+Bt+Cdt=\int\frac{1}{\sqrt{A}}\times{\sqrt{A}}\times\sqrt{At^2+Bt+C}dt=∫A1×A×At2+Bt+Cdt
=∫1A×A2t2+ABt+ACdt=\int\frac{1}{\sqrt{A}}\times\sqrt{A^2t^2+ABt+AC}dt=∫A1×A2t2+ABt+ACdt
=∫1A×(At+B2)2+(4AC−B24)2dt=\int\frac{1}{\sqrt{A}}\times\sqrt{(At+\frac{B}{2})^2+(\sqrt{\frac{4AC-B^2}{4}})^2}dt=∫A1×(At+2B)2+(44AC−B2)2dt
=∫1A×(At+B2)2+(4AC−B24)2×1A×d(At+B2)=\int\frac{1}{\sqrt{A}}\times\sqrt{(At+\frac{B}{2})^2+(\sqrt{\frac{4AC-B^2}{4}})^2}\times \frac{1}{A} \times d(At+\frac{B}{2})=∫A1×(At+2B)2+(44AC−B2)2×A1×d(At+2B)
=1AA×∫(At+B2)2+(4AC−B24)2×d(At+B2)=\frac{1}{A\sqrt{A}}\times\int\sqrt{(At+\frac{B}{2})^2+(\sqrt{\frac{4AC-B^2}{4}})^2} \times d(At+\frac{B}{2})=AA1×∫(At+2B)2+(44AC−B2)2×d(At+2B)
令u=At+B2u=At+\frac{B}{2}u=At+2B,a=4AC−B24a=\sqrt{\frac{4AC-B^2}{4}}a=44AC−B2,我们就得到了∫x2+a2dx\int\sqrt{x^2+a^2}dx∫x2+a2dx型不定积分,即1AA∫u2+a2du\frac{1}{A\sqrt{A}}\int\sqrt{u^2+a^2}duAA1∫u2+a2du,这个时候,积分变量从ttt变成了uuu,因为对ttt的积分区间是t∈[0,1]t\in[0,1]t∈[0,1]且u=At+B2u=At+\frac{B}{2}u=At+2B,所以对uuu的积分区间为u∈[B2,A+B2]u\in[\frac{B}{2},A+\frac{B}{2}]u∈[2B,A+2B],所以我们可以得出:
∫01(x′)2+(y′)2dt\int_0^1\sqrt{(x')^2+(y')^2}dt∫01(x′)2+(y′)2dt
=∫01At2+Bt+Cdt= \int_0^1\sqrt{At^2+Bt+C}dt=∫01At2+Bt+Cdt
=1AA∫B2A+B2u2+a2du= \frac{1}{A\sqrt{A}}\int_{\frac{B}{2}}^{A+\frac{B}{2}}\sqrt{u^2+a^2}du=AA1∫2BA+2Bu2+a2du (u=At+B2u=At+\frac{B}{2}u=At+2B,a=4AC−B24a=\sqrt{\frac{4AC-B^2}{4}}a=44AC−B2)
=1AA×[A+B22(A+B2)2+a2+a22ln∣A+B2+(A+B2)2+a2∣−(B4B44+a2+a22ln∣B2+B24+a2∣)]= \frac{1}{A\sqrt{A}}\times\bigg[\frac{A+\frac{B}{2}}{2}\sqrt{(A+\frac{B}{2})^2+a^2}+\frac{a^2}{2}\ln\bigg\lvert A+\frac{B}{2}+\sqrt{(A+\frac{B}{2})^2+a^2}\bigg\rvert - \bigg(\frac{B}{4}\sqrt{\frac{B^4}{4}+a^2}+\frac{a^2}{2}\ln\bigg\lvert \frac{B}{2}+\sqrt{\frac{B^2}{4}+a^2}\bigg\rvert\bigg)\bigg]=AA1×[2A+2B(A+2B)2+a2+2a2lnA+2B+(A+2B)2+a2−(4B4B4+a2+2a2ln2B+4B2+a2)]
接下来就是把各个常量代进去了。结果≈1.6232\approx1.6232≈1.6232
3.2.4 代码实现
3.2.4.1 求二阶贝塞尔曲线的弧长
export const getQuadraticBezierLength = (
P0X: number,
P0Y: number,
P1X: number,
P1Y: number,
P2X: number,
P2Y: number
) => {
const ax = 2 * (P0X - 2 * P1X + P2X)
const bx = -2 * (P0X - P1X)
const ay = 2 * (P0Y - 2 * P1Y + P2Y)
const by = -2 * (P0Y - P1Y)
const A = ax * ax + ay * ay
const B = 2 * (ax * bx + ay * by)
const C = bx * bx + by * by
const a = Math.sqrt((4 * A * C - B * B) / 4)
// 牛顿-莱布尼兹公式
const F1 =
(A / 2 + B / 4) * Math.sqrt((A + B / 2) * (A + B / 2) + a * a) +
((a * a) / 2) *
Math.log(
Math.abs(A + B / 2 + Math.sqrt((A + B / 2) * (A + B / 2) + a * a))
)
const F0 =
(B / 4) * Math.sqrt((B * B) / 4 + a * a) +
((a * a) / 2) * Math.log(B / 2 + Math.sqrt((B * B) / 4 + a * a))
const length = (1 / (Math.sqrt(A) * A)) * (F1 - F0) // 不要忘了前面还有个(A根号A分之一)
return length
}虽然公式很长,但是代码看起来就短多了。
3.2.4.2 采样多个点,然后连成一个近似于二阶贝塞尔曲线的直边多边形
public quadraticCurveTo(cpX: number, cpY: number, toX: number, toY: number) {
const len = this.currentPath.points.length
if (len === 0) {
this.currentPath.points = [0, 0]
}
const P0X = this.currentPath.points[len - 2]
const P0Y = this.currentPath.points[len - 1]
const P1X = cpX
const P1Y = cpY
const P2X = toX
const P2Y = toY
// 求出这条二阶贝塞尔曲线的长度
const curveLength = getQuadraticBezierLength(P0X, P0Y, P1X, P1Y, P2X, P2Y)
let segmentsCount = Math.ceil(curveLength / 10) // 每10个像素采样一次
// 最大2048份
if (segmentsCount > 2048) {
segmentsCount = 2048
}
// 最小8份
if (segmentsCount < 8) {
segmentsCount = 8
}
// 计算出采样点的坐标然后放入points数组
for (let i = 1; i <= segmentsCount; i++) {
const t = i / segmentsCount
// 直接套用二阶贝塞尔曲线的公式
const x = (1 - t) * (1 - t) * P0X + 2 * t * (1 - t) * P1X + t * t * P2X
const y = (1 - t) * (1 - t) * P0Y + 2 * t * (1 - t) * P1Y + t * t * P2Y
this.currentPath.points.push(x, y)
}
return this
}3.3 三阶贝塞尔曲线
我们用4个点来表示一条三阶贝塞尔曲线,这3个点分别是P0P_0P0、P1P_1P1、P2P_2P2和P3P_3P3,他们分别代表着这条三阶贝塞尔曲线的起始点、控制点1、控制点2、终点。如果对贝塞尔曲线不太熟悉,可以去看看这几篇文章
深入理解贝塞尔曲线
如何理解并应用贝塞尔曲线
3.3.1 如何计算三阶贝塞尔曲线的弧长
与二阶贝塞尔曲线类似,我们会采样多个曲线上的点,然后把这些点连起来,就得到了一条近似的三阶贝塞尔曲线,三阶贝塞尔曲线的参数方程如下:
{x=(1−t)3×P0x+3t(1−t)2×P1x+3t2(1−t)×P2x+t3×P3xy=(1−t)3×P0y+3t(1−t)2×P1y+3t2(1−t)×P2y+t3×P3y\begin{cases} x=(1-t)^3\times P_0x + 3t(1-t)^2 \times P_1x + 3t^2(1-t) \times P_2x + t^3 \times P_3x \\ y=(1-t)^3\times P_0y + 3t(1-t)^2 \times P_1y + 3t^2(1-t) \times P_2y + t^3 \times P_3y \end{cases}{x=(1−t)3×P0x+3t(1−t)2×P1x+3t2(1−t)×P2x+t3×P3xy=(1−t)3×P0y+3t(1−t)2×P1y+3t2(1−t)×P2y+t3×P3y
与二阶贝塞尔曲线类似,我们可以得到三阶贝塞尔曲线弧长的积分表达式为:∫01(x′)2+(y′)2dt\int_0^1\sqrt{(x')^2+(y')^2}dt∫01(x′)2+(y′)2dt,将参数方程中的xxx和yyy代入,然后把一些常数凑到一起并用另一些常数来替换,我们可以得到:
∫(x′)2+(y′)2dt=∫At4+Bt3+Ct2+Dt+Edt\int\sqrt{(x')^2+(y')^2}dt=\int\sqrt{At^4+Bt^3+Ct^2+Dt+E}dt∫(x′)2+(y′)2dt=∫At4+Bt3+Ct2+Dt+Edt
接下来我们要怎么求这个函数的不定积分呢?答案是:直接放弃
「这个函数的不定积分由于根号内的ttt的次数太高了,已经没法求了,我们只能另辟蹊径。」
3.3.2 分段+勾股定理
我们将会在三阶贝塞尔曲线上采样10个点,然后得到这些点的坐标,这样我们就得到了一系列的线段,我们用勾股定理来求出这些线段的长度之和,这样就得到了三阶贝塞尔曲线的长度的近似值,如下图所示:
代码如下:
export const getBezierLength = (
P0X: number,
P0Y: number,
P1X: number,
P1Y: number,
P2X: number,
P2Y: number,
P3X: number,
P3Y: number
) => {
const n = 10 // 取10段
let x = P0X
let y = P0Y
let length = 0
for (let i = 1; i <= n; i++) {
const t = i / n
const newX =
(1 - t) * (1 - t) * (1 - t) * P0X +
3 * t * (1 - t) * (1 - t) * P1X +
3 * t * t * (1 - t) * P2X +
t * t * t * P3X
const newY =
(1 - t) * (1 - t) * (1 - t) * P0Y +
3 * t * (1 - t) * (1 - t) * P1Y +
3 * t * t * (1 - t) * P2Y +
t * t * t * P3Y
const dx = newX - x
const dy = newY - y
length += Math.sqrt(dx * dx + dy * dy)
x = newX
y = newY
}
return length
}3.3.3 采样多个点,然后连成一个近似于三阶贝塞尔曲线的直边多边形
接下来的事情就跟处理二阶贝塞尔曲线的方式差不多了,我们已经得到了三阶贝塞尔曲线的长度,然后计算出
n的大小,最后采样n个点,将这些点用直线连接起来。
代码如下:
public bezierCurveTo(
cpX: number,
cpY: number,
cpX2: number,
cpY2: number,
toX: number,
toY: number
) {
const len = this.currentPath.points.length
if (len === 0) {
this.currentPath.points = [0, 0]
}
const P0X = this.currentPath.points[len - 2]
const P0Y = this.currentPath.points[len - 1]
const P1X = cpX
const P1Y = cpY
const P2X = cpX2
const P2Y = cpY2
const P3X = toX
const P3Y = toY
// 求出这条三阶贝塞尔曲线的长度
const curveLength = getBezierLength(P0X, P0Y, P1X, P1Y, P2X, P2Y, P3X, P3Y)
let segmentsCount = Math.ceil(curveLength / 10) // 每10个像素采样一次
// 最大2048份
if (segmentsCount > 2048) {
segmentsCount = 2048
}
// 最小8份
if (segmentsCount < 8) {
segmentsCount = 8
}
// 计算出采样点的坐标然后放入points数组
for (let i = 1; i <= segmentsCount; i++) {
const t = i / segmentsCount
// 直接套用三阶贝塞尔曲线的公式
const x =
(1 - t) * (1 - t) * (1 - t) * P0X +
3 * t * (1 - t) * (1 - t) * P1X +
3 * t * t * (1 - t) * P2X +
t * t * t * P3X
const y =
(1 - t) * (1 - t) * (1 - t) * P0Y +
3 * t * (1 - t) * (1 - t) * P1Y +
3 * t * t * (1 - t) * P2Y +
t * t * t * P3Y
this.currentPath.points.push(x, y)
}
return this
}3.3.4 效果图
二阶和三阶贝塞尔曲线: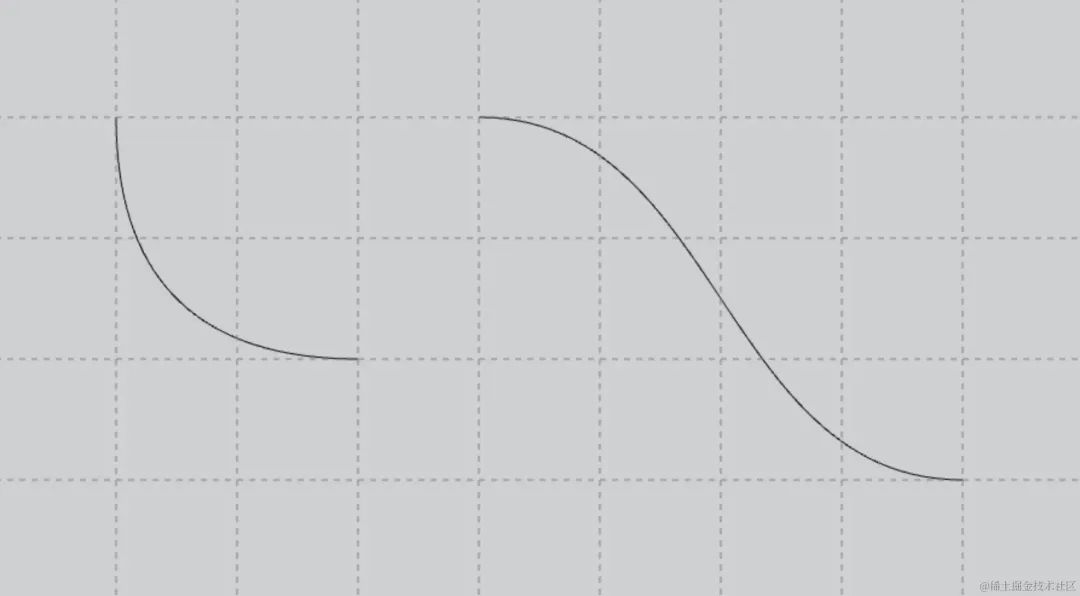
接下来我们处理曲线的方式跟处理贝塞尔曲线的方式是差不多的,即:先求出曲线的长度,然后求出采样的点的个数
n,然后采样n个点,最后把这些点连接起来,就得到了一条近似的曲线。
3.4 圆弧arc
这里的arc函数尽量保持和canvas原生的arc函数的逻辑相同
3.4.1 代码
圆弧的代码比贝塞尔曲线简单多了,直接上代码:
public arc(
cx: number,
cy: number,
radius: number,
startAngle: number,
endAngle: number,
anticlockwise = false
) {
if (!anticlockwise) {
while (endAngle < startAngle) {
endAngle += Math.PI * 2
}
if (endAngle - startAngle > Math.PI * 2) {
endAngle = startAngle + Math.PI * 2
}
}
if (anticlockwise) {
while (endAngle > startAngle) {
startAngle += Math.PI * 2
}
if (startAngle - endAngle > Math.PI * 2) {
endAngle = startAngle - Math.PI * 2
}
}
const diff = endAngle - startAngle
if (diff === 0) {
return this
}
const startX = cx + Math.cos(startAngle) * radius
const startY = cy + Math.sin(startAngle) * radius
this.lineTo(startX, startY)
const curveLen = Math.abs(diff) * radius // 角度(弧度制)乘以半径等于弧长
let segmentsCount = Math.ceil(curveLen / 10)
// 最大2048份
if (segmentsCount > 2048) {
segmentsCount = 2048
}
// 最小8份
if (segmentsCount < 8) {
segmentsCount = 8
}
for (let i = 1; i <= segmentsCount; i++) {
const angle = startAngle + diff * (i / segmentsCount)
const x = cx + Math.cos(angle) * radius
const y = cy + Math.sin(angle) * radius
this.lineTo(x, y)
}
return this
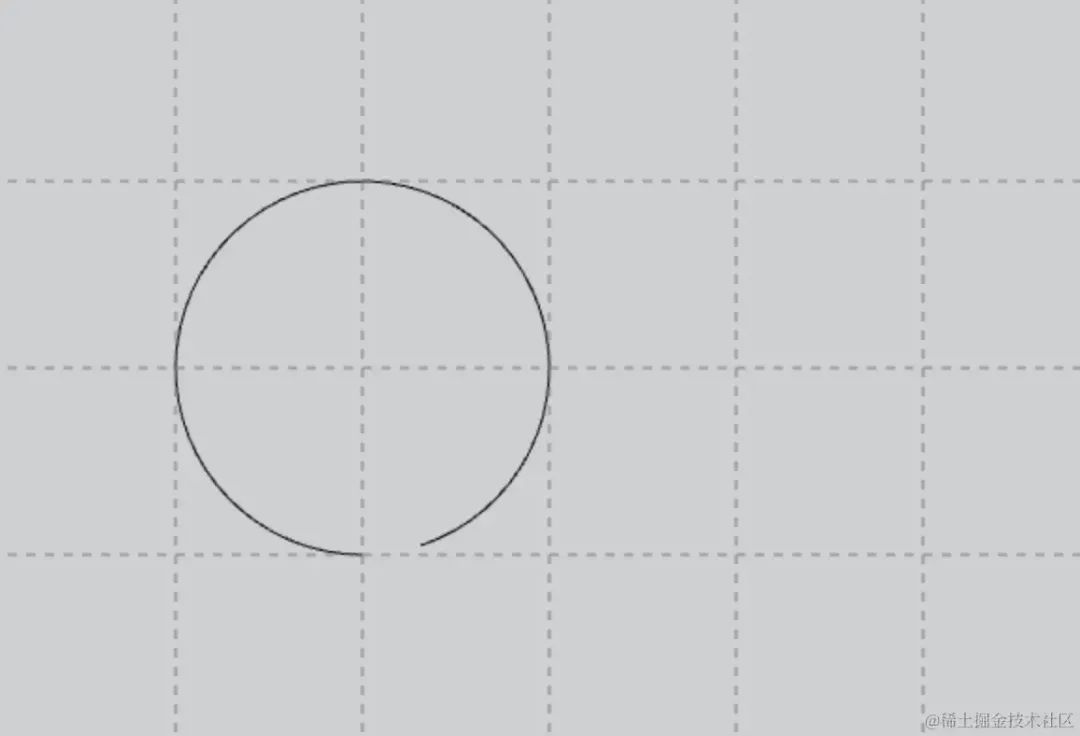
}3.4.2 效果
const cir = new Graphics()
cir.lineStyle(1)
cir.arc(200, 200, 100, Math.PI * 2.4, Math.PI * 6.5, true)
app.stage.addChild(cir)3.5 圆弧arcTo
arcTo可以比较方便地用来构建一些具有圆角的图形,这个函数将会借用arc函数的能力来绘制圆弧,我们要做的就是求出
圆心坐标,起始角度和结束角度,以及是否逆时针。
3.5.1 代码
public arcTo(x1: number, y1: number, x2: number, y2: number, radius: number) {
const len = this.currentPath.points.length
/**
* 如果画笔当前没有落点,则该操作相当于moveTo(x1, y1)
* 如果半径为0,则该操作也相当于lineTo(x1, y1)
*/
if (len === 0 || radius === 0) {
this.lineTo(x1, y1)
return this
}
/**
* 假设画笔落点为P0,控制点1为P1,控制点2为P2,如果向量P0P1和向量P1P2的夹角太小或者夹角接近180度,
* 或者向量P0P1或向量P1P2其中一个的长度为0,
* 那么该操作也相当于moveTo(x1, y1),
* 我们用叉积来判断这种情况
*/
const a1 = this.currentPath.points[len - 1] - y1
const b1 = this.currentPath.points[len - 2] - x1
const a2 = y2 - y1
const b2 = x2 - x1
const crossProduct = a1 * b2 - b1 * a2
const mm = Math.abs(crossProduct)
if (mm < 1.0e-8) {
this.lineTo(x1, y1)
return this
}
const dd = a1 * a1 + b1 * b1
const cc = a2 * a2 + b2 * b2
const tt = a1 * a2 + b1 * b2
const k1 = (radius * Math.sqrt(dd)) / mm
const k2 = (radius * Math.sqrt(cc)) / mm
const j1 = (k1 * tt) / dd
const j2 = (k2 * tt) / cc
const cx = k1 * b2 + k2 * b1
const cy = k1 * a2 + k2 * a1
const px = b1 * (k2 + j1)
const py = a1 * (k2 + j1)
const qx = b2 * (k1 + j2)
const qy = a2 * (k1 + j2)
const startAngle = Math.atan2(py - cy, px - cx)
const endAngle = Math.atan2(qy - cy, qx - cx)
const anticlockwise = b1 * a2 > b2 * a1
return this.arc(
cx + x1,
cy + y1,
radius,
startAngle,
endAngle,
anticlockwise
)
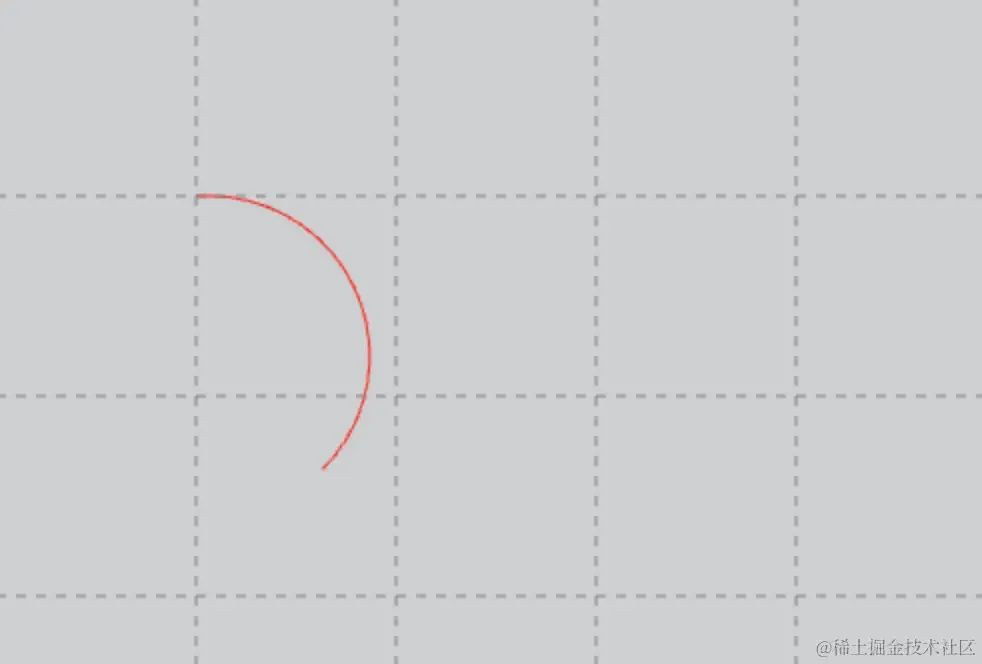
}3.5.2 效果
const cir = new Graphics()
.lineStyle(1, 'red')
.moveTo(100, 100)
.arcTo(300, 100, 200, 200, 80)
app.stage.addChild(cir)3.6 来一个完整的路径
目前所有的图形都讲述完毕了,接下来将用这些图形来构造一个完整的路径
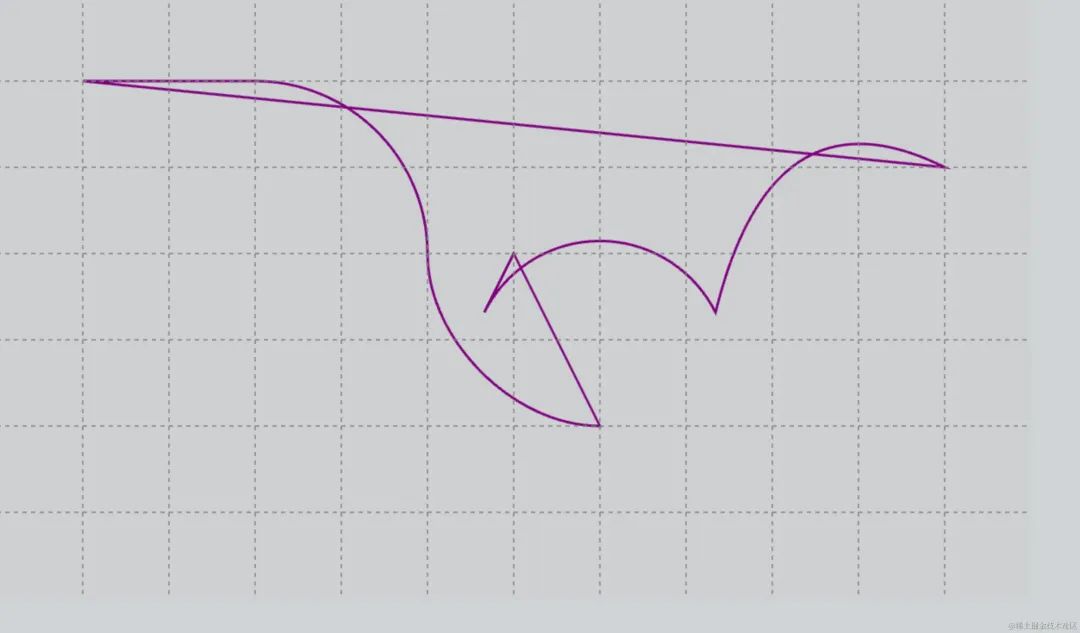
3.6.1 代码
const path = new Graphics()
.lineStyle(3, 'purple')
.moveTo(100, 100)
.lineTo(300, 100)
.arc(300, 300, 200, Math.PI * 1.5, Math.PI * 2)
.bezierCurveTo(500, 400, 600, 500, 700, 500)
.lineTo(600, 300)
.arcTo(700, 100, 800, 300, 150)
.quadraticCurveTo(900, 100, 1100, 200)
.closePath()
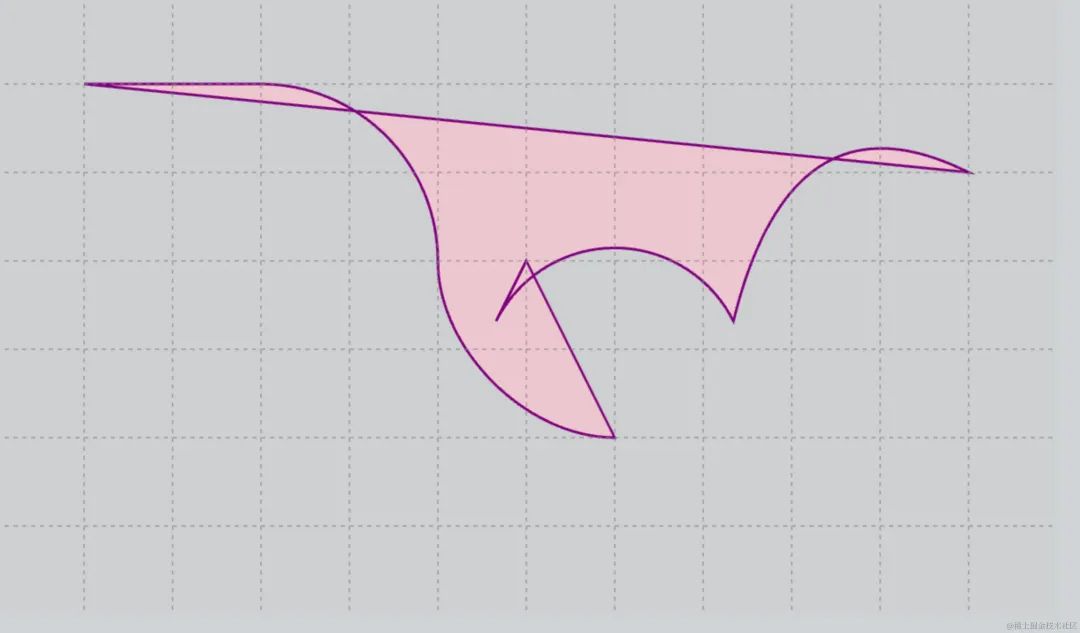
app.stage.addChild(path)3.6.2 效果
不加填充
加上填充
.beginFill('pink', 0.6)4 最后
本篇讲述了如何构建一些简单图形以及一些比较复杂的曲线图形,到这里,我们已经可以利用Graphics类来构建所有的复杂图形了,对于一些曲线图形我们会采用「直边多边形」近似的方式来构建,这是为「碰撞检测」做准备的,也就是下一篇要讲述的内容。