五分钟了解一致性哈希算法

理论

一致性哈希算法是一种常用的分布式算法，其主要用途是在分布式系统中，将数据根据其键（key）进行散列（hash），然后将散列结果映射到环上，再根据数据节点的数量，将环划分为多个区间，每个节点负责处理环上一定区间范围内的数据。

普通哈希的问题

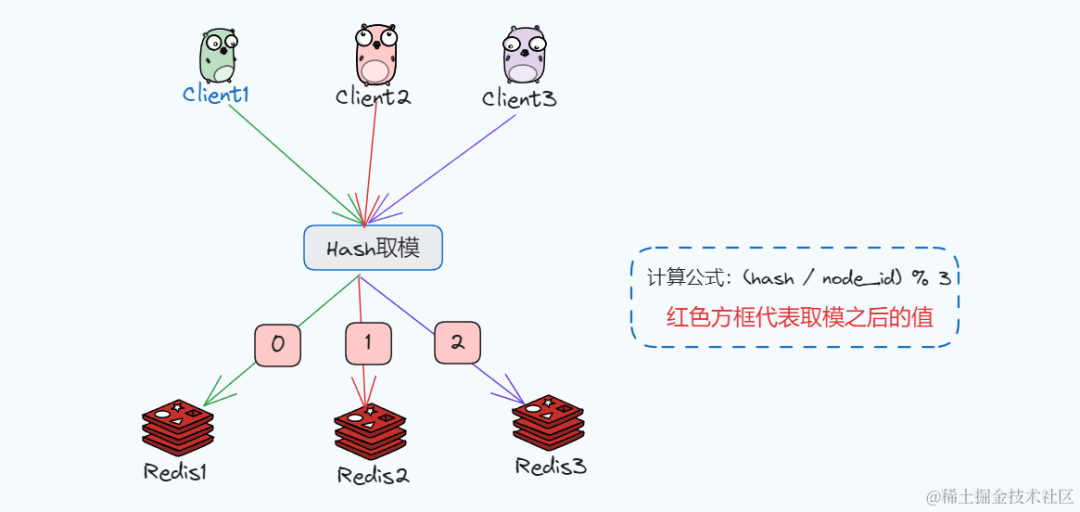
分布式集群中，对机器的添加删除，或者机器故障后自动脱离集群这些操作是集群管理最基本的功能。如果采用常用的hash(object)%N取模的方式，在节点进行添加或者删除后，需要重新进行迁移改变映射关系，否则可能导致原有的数据无法找到。

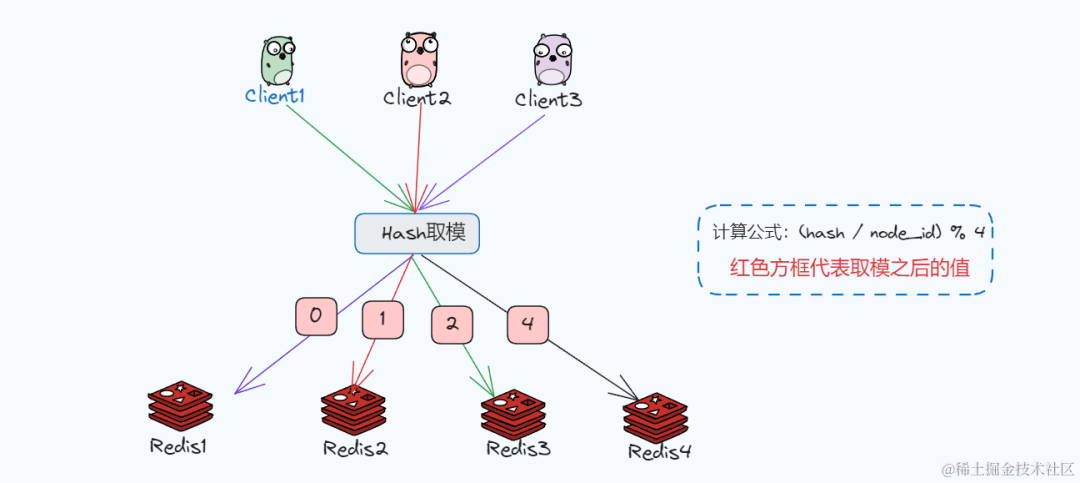
举个栗子

随着业务和流量的增加，假如我们的Redis查询服务节点扩展到了3个，为了将查询请求进行均衡，每次请求都在相同的Redis中，使用hv = hash(key) % 3的方式计算，对每次查询请求都通过hash值计算，得出来0、1 、2的值分别对应服务节点的编号，计算得到的hv的值就去对应的节点处理。

但是这里有个问题，服务增减是需要对此时的key进行重新计算，比如减少一个服务的时候，此时需要按 hv = hash(key) % 2计算，而增加一个服务节点的时候需要按hv = hash(key) % 4计算，而这种取模基数的变化会改变大部分原来的映射关系，导致数据查询不到。

这个时候只能进行数据迁移，真是太麻烦了，而一致性哈希算法显然是一个更好选择！

一致性hash算法

一致性哈希同样使用了取模的方式，不同的是对 2^32 这个固定的值进行取模运算。

在使用一致哈希算法后，哈希表槽位数（大小）的改变平均只需要对 K/n 个关键字重新映射，其中K是关键字的数量， n是槽位数量，而不需要对所有的映射关系进行重新映射！

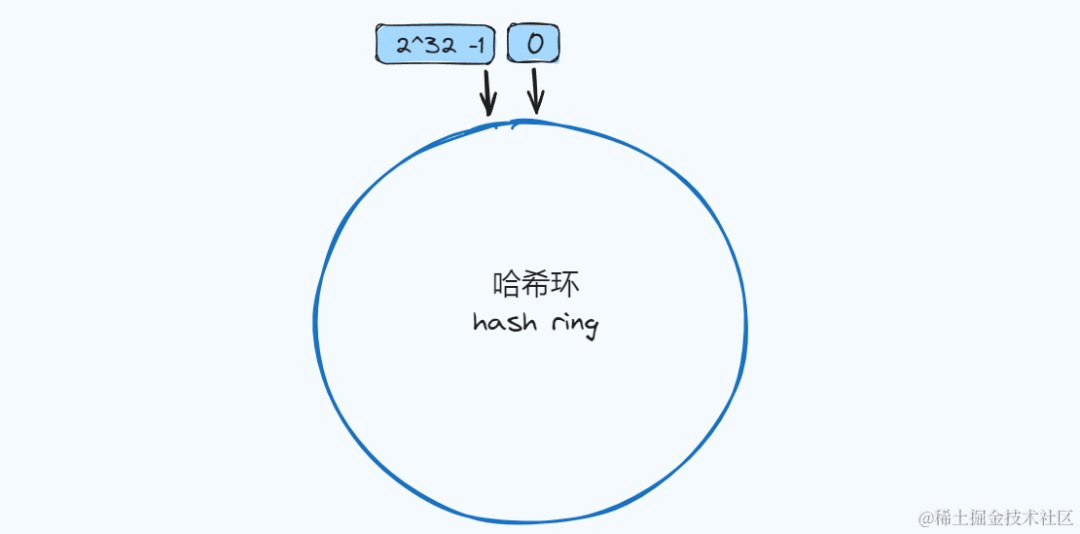
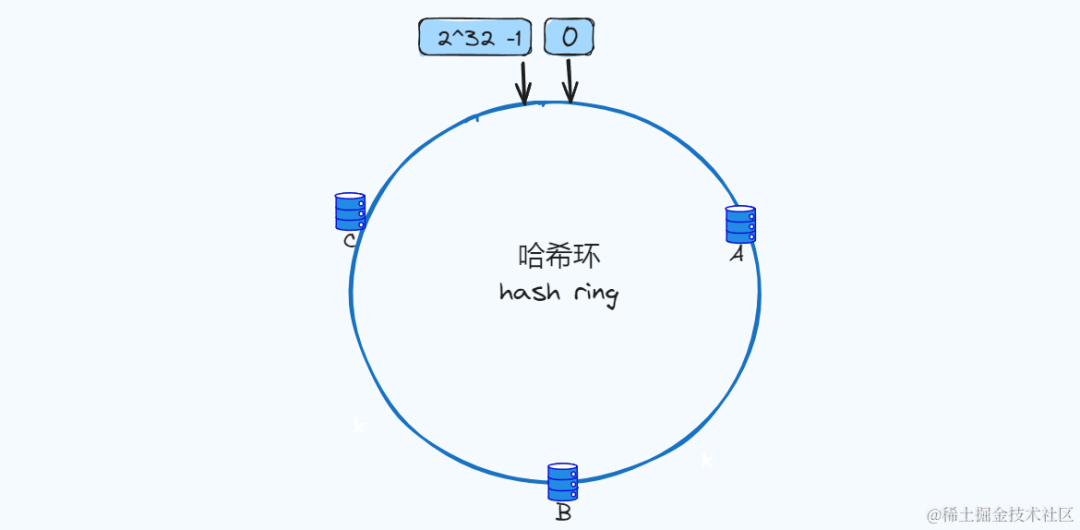
Hsh环

我们可以把一致哈希算法是对 2^32 进行取模运算的结果值虚拟成一个圆环，环上的刻度对应一个 0~2^32 - 1 之间的数值，如下图：

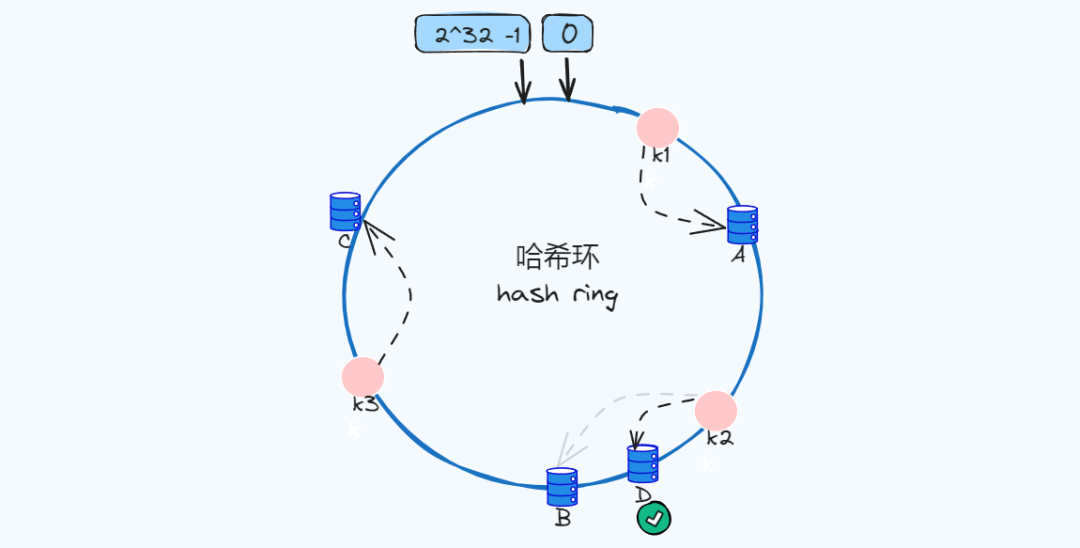
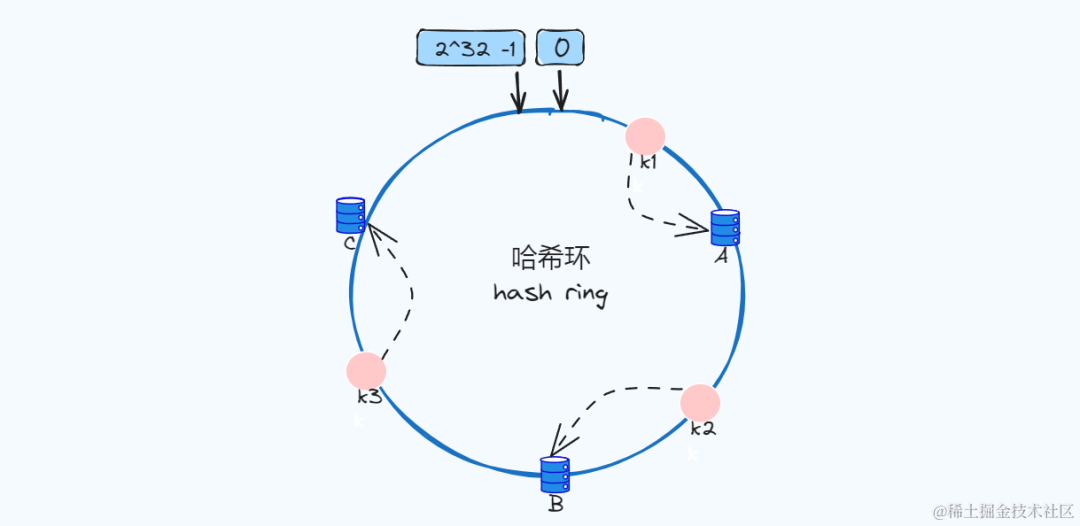
节点入环

下图我们三个节点（A/B/C）经过哈希计算，放入下面环中，一般我们会根据服务器的IP或者唯一别名进行哈希计算。

那数据是如何进行关系映射呢，同样key值经过哈希之后，结果映射到哈希环上，然后将结果值按顺时针方向找到离自己最近的节点上，将value存储到那个节点上。

如下图：

k1、k2、k3经过哈希计算后在哈希环的位置，顺时针方向找到离自己最近的节点，比如k1最近的节点是A，节点A就是存储 k1数据value的节点。

新增节点

新增加点D，节点的数量增加到了四个，而此时k2最近的节点是D，所以会迁移到D，k1和k3不受影响

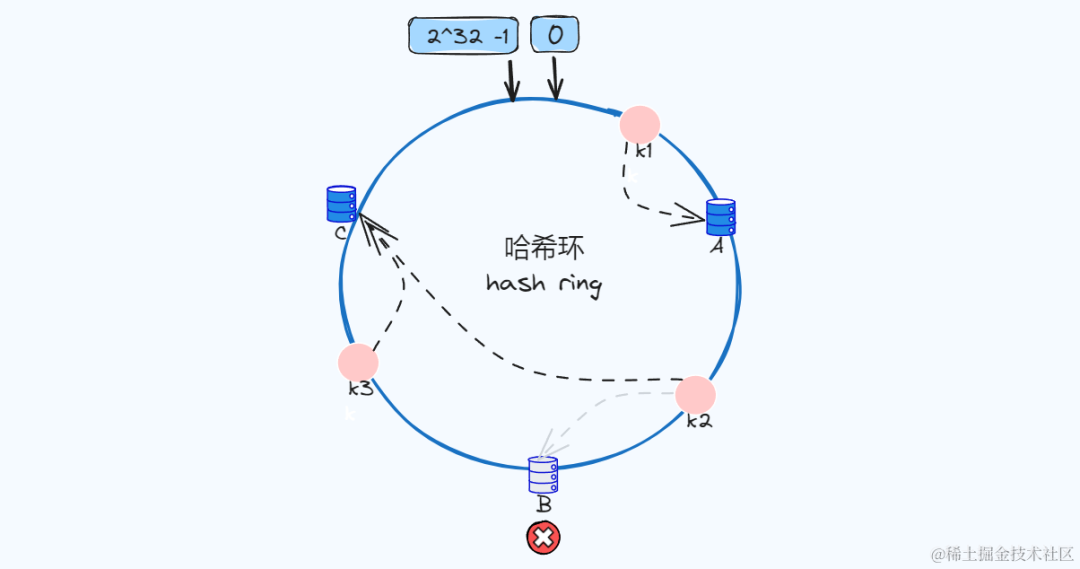
删除节点

删除节点B之后，存储在B节点上的k2，将会重新映射找到离它最近的节点C，此时k2的数据存储在C节点上，k1、k3不受影响。

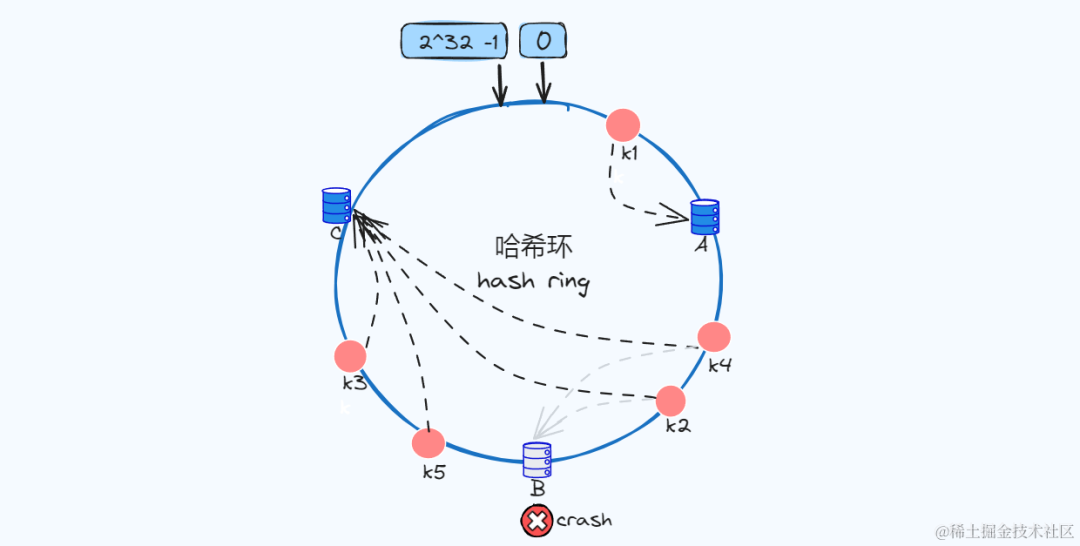
不平衡问题

我们通过新增节点和删除节点，知道了该方式会影响该节点的顺时针的后一个节点，其他节点不受影响。

但是因为生成哈希值的分布并不是均匀的，如下图新增k4、k5，如果节点B宕机了，k2和k4也迁移到节点C，导致那么大部分请求就落到节点C了，如果数量更多呢，此时会导致节点C压力陡增，这样就不均衡了！

那如何解决这个问题呢？

那就是通过 虚拟节点

虚拟节点

虚拟节点 可以理解为是作为实际节点的一个copy，多个虚拟节点映射一个实际节点，因为在哈希环上节点越多就分布的越均匀，即使我们现实中不会有那么多真实节点。

上图中三个真实节点A、B、C，映射了9个虚拟节点，如果key值经过哈希落到临近A-1、A-2、A-3的虚拟节点，那么最终都将映射到真实节点A，你想如果虚拟节点再多点，是不是就会更均衡了！

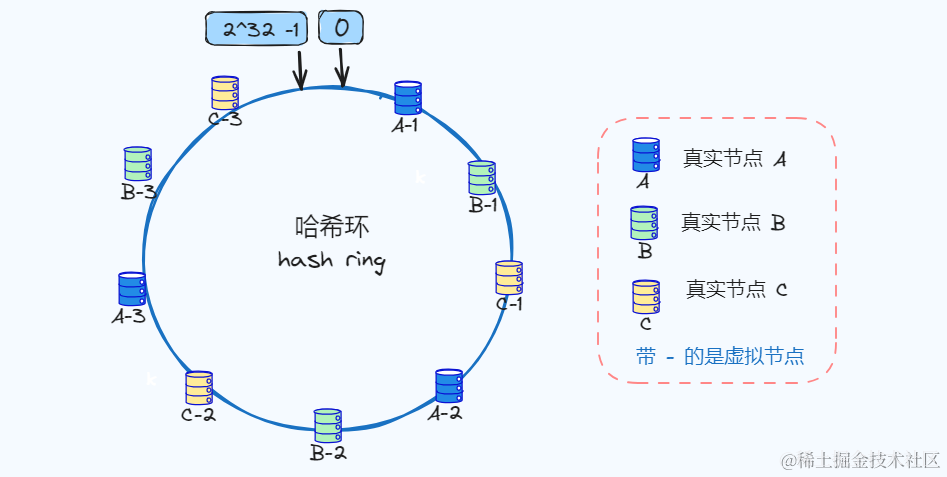
假设真实节点A被移除，A对应虚拟节点也会移除，但是多虚拟节点方式可以映射更多真实节点，让剩余的节点更好得去承担节点变化的请求压力！

如下图：

这里简单讲解一下，图中真实节点A被移除，那么对应的虚拟节点移除，那么此时k1的重新映射到C-1、k3重新映射到B-3，也就是说被迁移到真实节点B和C，由此可见节点被移除会被更均衡的分散到其他节点上。

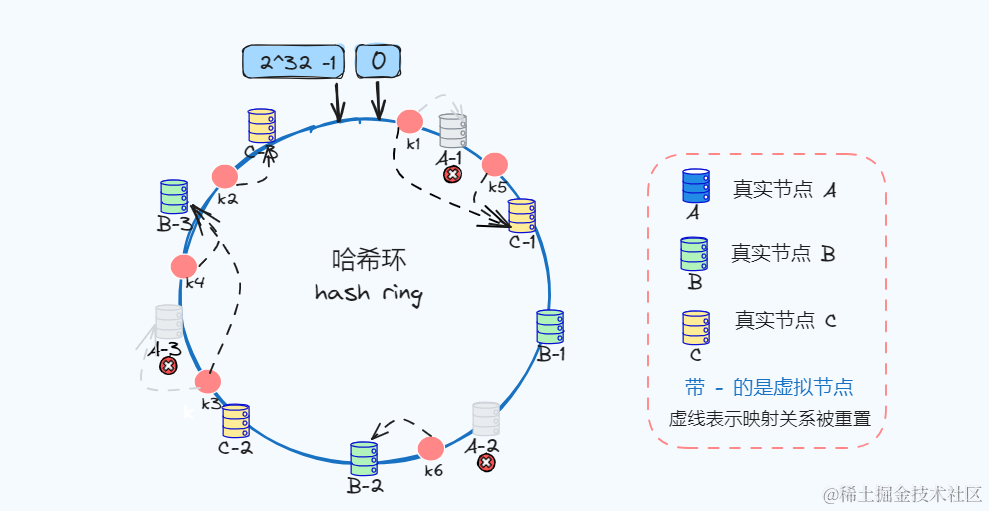
图中只简单列举了几个虚拟节点，虚拟节点越多，相对会越均衡。

好了，今天关于一致性哈希算法的介绍就到这了！