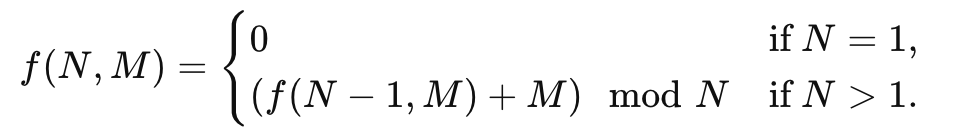一张图看懂刘谦的魔术

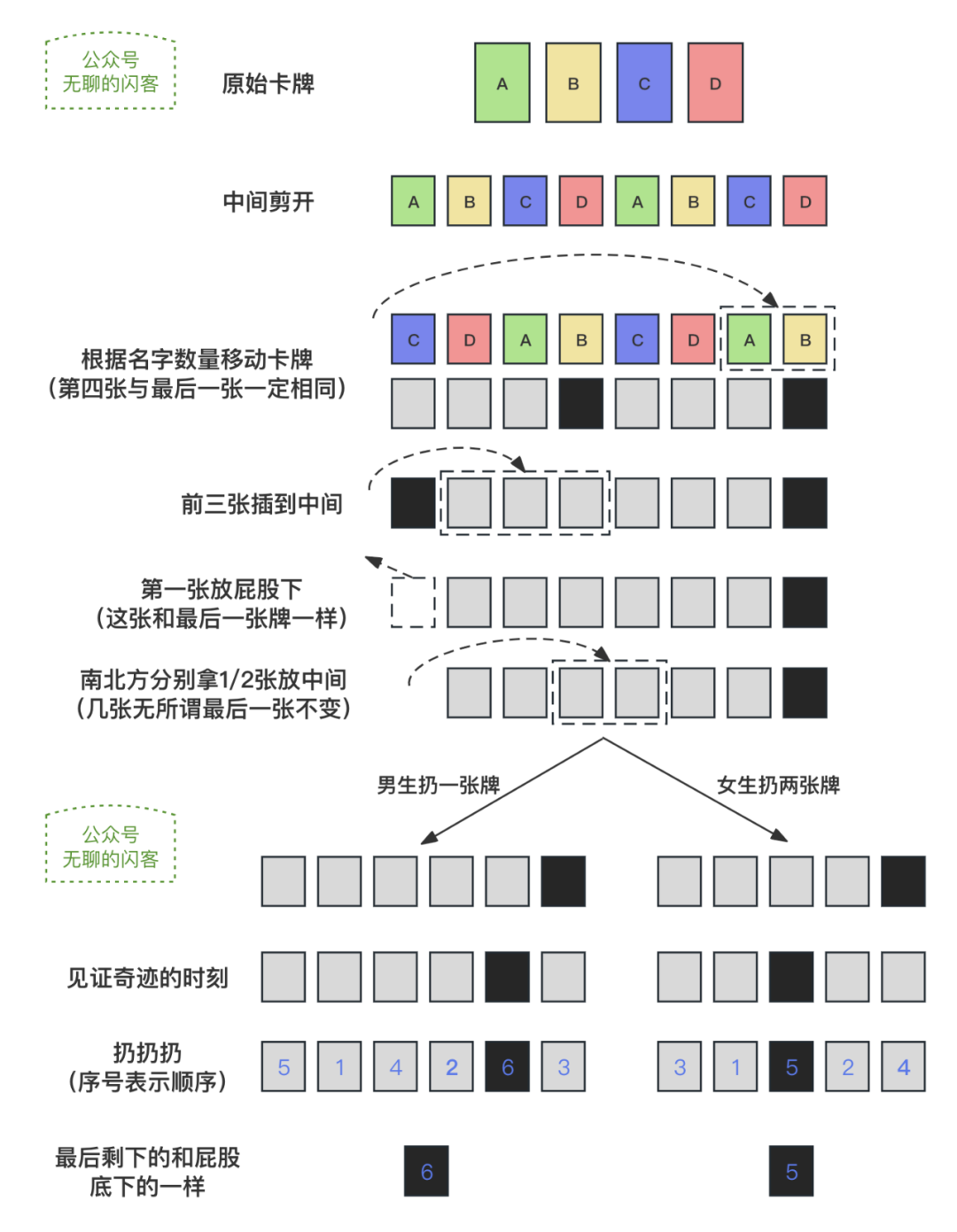
今年刘谦最后的魔术是个综合的数学问题，一张图就可以说明白了。

下面展开解释一下，如果只想把直接原因想明白，大家停下来几秒钟看上图就可以啦。如果想听我多说说这里面的门道，可以接着往下面看。

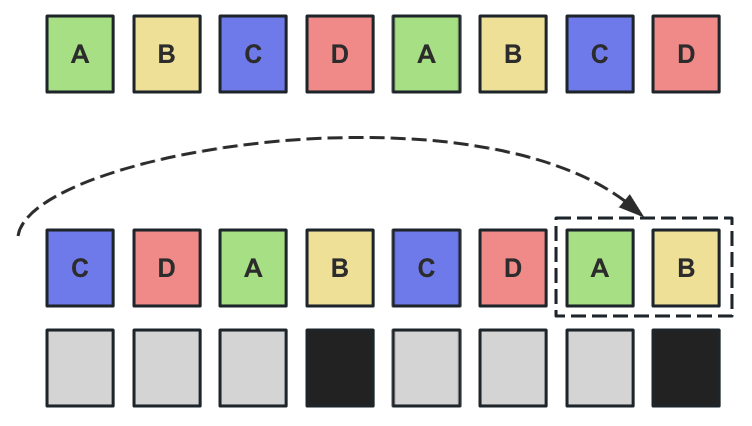
原始卡牌从中间剪开，再放到一起，这形成了一个 ABCDABCD 的模式。不论依次移动多少张头部的卡片放到尾部，第四张牌永远与最后一张牌相同。

这其实拍脑袋就能很快想明白，但如果你想多想一步为什么的话，我的想法是从周期函数的角度看，ABCD 可以理解为一个函数的最小正周期。就相当于：

F(x) = F(x+4)

依次移动 N 张卡牌就相当于：

F(x+N) = F(x+4+N)

依然是周期函数值相等的地方。

如果从群论的角度看，字符串 ABCDABCD 的所有置换可以构成一个循环群，其元素就是所有置换操作（将第一张牌移动到最后一张这个操作的幂次），二元运算符就是两个置换操作的复合。

我群论只学到了些皮毛，有大佬的话可以展开讲讲从这个层次理解这件事，会有什么新的发现。

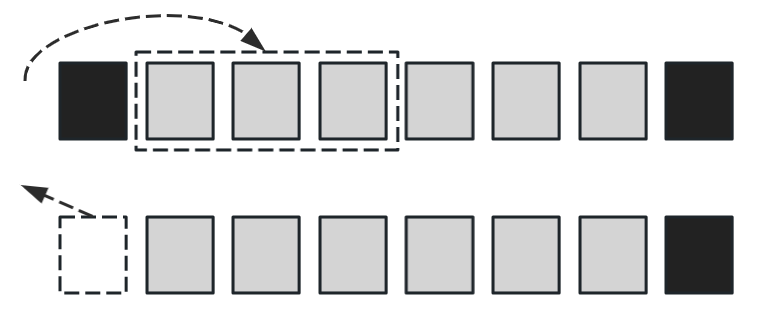
接下来我们选择开头的三张牌放到中间，那么第四张牌就变到了第一个位置上，此时我们把第一张牌藏起来。这其实就相当于直接把一开始的第四张牌藏起来。那么后续的操作只需要保证和第四张牌一样的最后一张牌被剩下来即可。

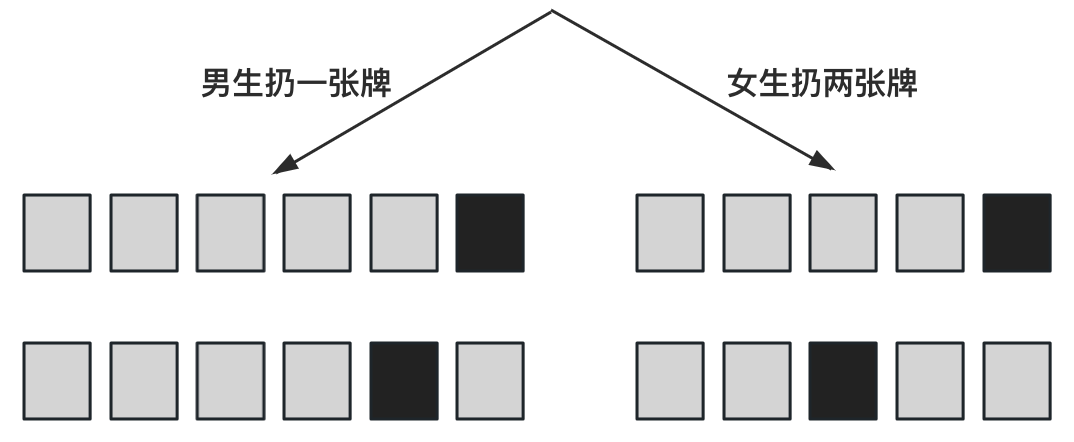
接下来分南北方分别将一张或者两张牌插到中间，这个步骤你也可以很容易发现，不论做多少步都是不影响的，我们只关注最后一张牌的变化即可。

接下来男生扔一张牌，女生扔两张牌，然后共同依次把 7 张（见证奇迹的时刻字数）头部的牌移动到尾部。这也没什么好说的，只看最后一张牌的位置，最终的操作就是变成了下面的样子。

这里有个小细节，就是如果只看最后一张牌的位置变化，那么把第一张牌放到后面，就相当于把最后一张牌往前挪一个位置，两者等价。

这里如果上升到群论的描述，就是由 ABCDABCD 的所有置换构成的群中，如果模掉了「只看最后一张牌其他牌都一样」这个等价关系，那么由「把第一张牌移动到最后」这个二元运算构成的群，和由「把最后一张牌向前移动一位」这个二元运算构成的群，是同构的。所以研究它们的一些性质时可以视为等价。

当然啦，这里纯是为了多想一点儿，实际情况完全没必要了。

再接下来，循环重复「把第一张牌放到最后，扔掉第一张」这个操作，最后剩下的牌保证了一定是图中黑色的。

这是个经典的约瑟夫问题，即 N 个人围成一个圈，按顺时针顺序从 1 到 N 编号。从第一个人开始，按顺时针方向数到第 M 个人，然后将其从圈中移除。

接下来从被移除人的下一个人开始，再数到第 M 个人，然后也将其移除。这个过程持续进行，直到圈中只剩下一个人。

那么剩下的这个人的编号可以由下面的递归公式得出。

在我们的这个问题里，男生那边就是一个 N = 6，M = 2 的约瑟夫问题。最后计算出的结果是 5，那么最后第 5 张卡片就会剩下。

女生那边就是一个 N = 5，M = 2 的约瑟夫问题。最后计算出的结果是 3，那么最后第 3 张卡片就会剩下。

约瑟夫问题只能通过递归公式一点一点计算，至今还没有找到一个通用的公式能直接计算出结果，这个问题也挺有趣，如果你能找到的话就厉害了。

但是当 M = 2 时，也就是数到第二个人就移除，相当于每隔一个人就移除一个。这个时候有比较巧妙的办法。

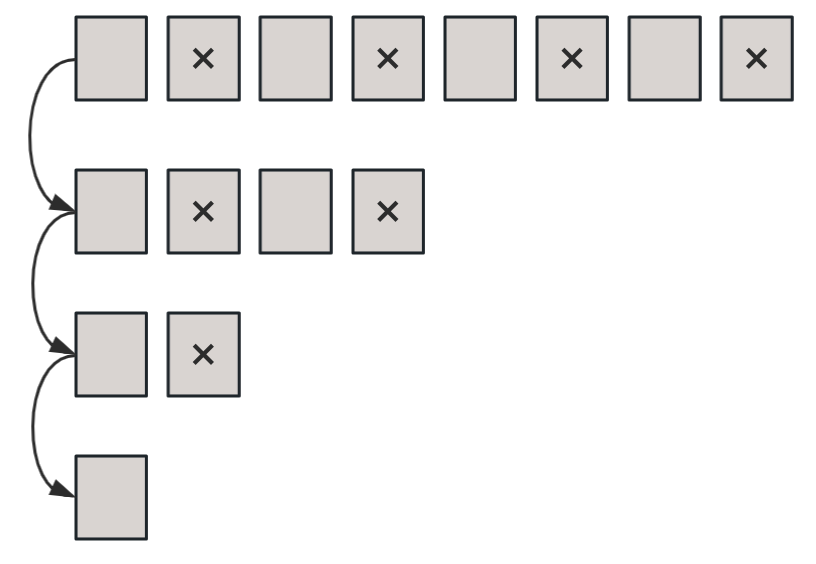
我们先试想下，当只有两个人（N = 2），1 号和 2 号时，那么直接移除 2 号，则 1 号留了下来。

如果有 4 个人（N = 4），那么第一轮 2 号和 4 号移除，此时还剩下 1 号和 3 号两个人。两个人的时候我们说了，最后还是 1 号留下，所以 4 个人最终还是 1 号留下。

继续想，如果有 8 个人（N = 8），那么第一轮之后，还剩下 4 个人，那么此时又和上一种情况一样了，所以最终剩下的还是 1 号。

所以，如果 N 是 2 的幂次，最后剩下的一定是 1 号。

也就是说，一开始不论 N 是多少，只要 N 的数量减少到 2 的幂次了，那么最后剩下的人一定就是当前刚刚一出的这个人后面的那个人。

用我们本次男生的扑克牌数量 N = 6 来说，就是扔掉两张牌后，还剩下 4 张牌，恰好是 2 的幂次了，后面那张牌就是最后会剩下的牌，也就是第 5 张。

回到通用的情况，也就是说，当 M = 2 时，最后剩下的牌的编号是：

先求出 N = 2ⁿ + R 里面的 R，这里的 R 就是去掉多少张牌后，剩下的牌刚好第一次达到 2 的幂次。

那么最后能剩下的牌的编号就是 2R + 1。因为每数两张牌才会去掉一张牌，所以要乘以 2。编号的位置是后面的那一个，所以要加 1。

好啦，至此本文解答完毕了刘谦魔术的秘密。

------

最后，由于本号的读者很多都是程序员，大家看看上面的计算过程，是否能够通过计算机的一些知识秒解出最后的结果呢？

提示一下，如果你想求出如下式子中的 R，是不是一下就找到了？

12499123 = 10ⁿ + R

对了，就是直接把首位的 1 去掉，就可以得到 R 的值了，这是因为我们在十进制下，处理 10 的幂次会比较直观。

那么我们只需要将 N 转换为二进制，就可以很快计算出在 2 的幂次下的 R 了。

比如 N = 6 时，二进制表示为 110

那么第一次达到 2 的幂次一定是二进制的 100，所以去掉开头的那个 1 就可以算出 R 了。那么 R 的值二进制表示就是 10

别急着转换为十进制，我们最终要计算 2R + 1，那么只需要将二进制左移一位，变成 100

然后再 +1 变成 101

最后再转换成十进制，也就是 5。

总结起来就是，去掉开头的 1，然后在结尾补个 1，就是最终的编号的二进制值。最后辛苦一下转换成十进制即可。

最后的最后，再留一道思考题。仔细回想下男生女生分别扔掉一张牌之后，男生剩 6 张牌，女生剩 5 张牌。

按照约瑟夫问题，男生需要将末尾的牌移动到位置 5，女生需要将末尾的牌移动到位置 3。

那么为什么像「见证奇迹的时刻」这样连续移动七次，就能分别做到将 6 张牌的末尾牌移动到位置 5，将 5 张牌的末尾牌移动到位置 3 呢？

更进一步讲，如果告诉你任意数量的两组牌（X, Y），让你分别移动到不同的位置处（M, N），你总能设计出同时满足两者的相同字数的话吗？